Abstract
We investigate, for two water models displaying a liquid–liquid critical point, the relation between changes in dynamic and thermodynamic anomalies arising from the presence of the liquid–liquid critical point. We find a correlation between the dynamic crossover and the locus of specific heat maxima 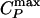 (“Widom line”) emanating from the critical point. Our findings are consistent with a possible relation between the previously hypothesized liquid–liquid phase transition and the transition in the dynamics recently observed in neutron scattering experiments on confined water. More generally, we argue that this connection between
(“Widom line”) emanating from the critical point. Our findings are consistent with a possible relation between the previously hypothesized liquid–liquid phase transition and the transition in the dynamics recently observed in neutron scattering experiments on confined water. More generally, we argue that this connection between 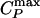 and dynamic crossover is not limited to the case of water, a hydrogen bond network-forming liquid, but is a more general feature of crossing the Widom line. Specifically, we also study the Jagla potential, a spherically symmetric two-scale potential known to possess a liquid–liquid critical point, in which the competition between two liquid structures is generated by repulsive and attractive ramp interactions.
and dynamic crossover is not limited to the case of water, a hydrogen bond network-forming liquid, but is a more general feature of crossing the Widom line. Specifically, we also study the Jagla potential, a spherically symmetric two-scale potential known to possess a liquid–liquid critical point, in which the competition between two liquid structures is generated by repulsive and attractive ramp interactions.
Keywords: liquid–liquid critical point, low-density liquid, high-density liquid, 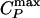 line,
line,  line
line
By definition, in a first-order phase transition, thermodynamic state functions such as density ρ and enthalpy H change discontinuously as we cool the system along a path crossing the equilibrium coexistence line (Fig. 1a, path β). However, in a real experiment, this discontinuous change may not occur at the coexistence line because a substance can remain in a supercooled metastable phase until a limit of stability (a spinodal) is reached (1) (Fig. 1b, path β).
Fig. 1.
Schematic phase diagram for the systems discussed in this article. (a) The critical region associated with a liquid–gas critical point. Shown are the two features displaying mathematical singularities: the critical point (filled circles) and the liquid–gas coexistence line (bold dashed curve). (b) Same as in a with the addition of the gas–liquid spinodal and the Widom line. Along the Widom line, thermodynamic response functions have extrema in their T dependence. Path α denotes a path along which the Widom line is crossed, whereas path β denotes a path crossing the coexistence line. (c) A hypothetical phase diagram for water of possible relevance to the recent neutron scattering experiments by Chen and colleagues (25, 26) on confined water. The negatively sloped liquid–liquid coexistence line generates a Widom line that extends beyond the critical point, suggesting that water may exhibit a fragile-to-strong transition for P < Pc (path α), whereas no dynamic changes will occur above the critical point (path β). (d) A sketch of the P–T phase diagram for the two-scale Jagla model. Upon cooling at constant pressure above the critical point (path α), the liquid changes, as the path crosses the Widom line, from a low-density state (characterized by a non-glassy Arrhenius dynamics) to a high-density state (characterized by non-Arrhenius dynamics) as the path crosses the Widom line. Upon cooling at constant pressure below the critical point (path β), the liquid remains in the LDL phase as long as path β does not cross the LDL spinodal line. Thus, one does not expect any dramatic change in the dynamic behavior along the path β.
If the system is cooled isobarically along a path above the critical pressure Pc (Fig. 1b, path α), the state functions continuously change from the values characteristic of a high-temperature phase (gas) to those characteristic of a low-temperature phase (liquid). The thermodynamic response functions, which are the derivatives of the state functions with respect to temperature (e.g., isobaric heat capacity CP = (∂H/∂T)P), have maxima at temperatures denoted Tmax(P). Remarkably, these maxima are still prominent far above the critical pressure (2–5), and the values of the response functions at Tmax(P) (e.g., 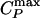 ) diverge as the critical point is approached. The lines of the maxima for different response functions asymptotically approach one another as the critical point is approached, because all response functions become expressible in terms of the correlation length. This asymptotic line is sometimes called the “Widom line” and is often regarded as an extension of the coexistence line into the “one-phase region.” If the system is cooled at constant pressure P0, and P0 is not too far from the critical pressure Pc, then there are two classes of behavior possible. (i) If P0 > Pc (path α), then experimentally measured quantities will change dramatically but continuously in the vicinity of the Widom line (with huge fluctuations as measured by, e.g., CP). (ii) If P0 < Pc (path β), experimentally measured quantities will change discontinuously if the coexistence line is actually seen. However, the coexistence line can be difficult to detect in a pure system because of metastability, and changes will occur only when the spinodal is approached where the gas phase is no longer stable. The changes in behavior may include not only static quantities like response functions (5) but also dynamic quantities like diffusivity.
) diverge as the critical point is approached. The lines of the maxima for different response functions asymptotically approach one another as the critical point is approached, because all response functions become expressible in terms of the correlation length. This asymptotic line is sometimes called the “Widom line” and is often regarded as an extension of the coexistence line into the “one-phase region.” If the system is cooled at constant pressure P0, and P0 is not too far from the critical pressure Pc, then there are two classes of behavior possible. (i) If P0 > Pc (path α), then experimentally measured quantities will change dramatically but continuously in the vicinity of the Widom line (with huge fluctuations as measured by, e.g., CP). (ii) If P0 < Pc (path β), experimentally measured quantities will change discontinuously if the coexistence line is actually seen. However, the coexistence line can be difficult to detect in a pure system because of metastability, and changes will occur only when the spinodal is approached where the gas phase is no longer stable. The changes in behavior may include not only static quantities like response functions (5) but also dynamic quantities like diffusivity.
In the case of water, the most important solvent for biological function (6, 7), a significant change in dynamical properties has been suggested to take place in deeply supercooled states (8–11). Unlike other network-forming materials (12), water behaves as a fragile liquid in the experimentally accessible window (9, 13, 14). Based on analogies with other network-forming liquids and with the thermodynamic properties of the amorphous forms of water, it has been suggested that, at ambient pressure, liquid water should show a crossover between fragile behavior at high T to strong behavior at low T (8, 15–19) in the deep supercooled region of the phase diagram below the homogeneous nucleation line. This region may contain the hypothesized liquid–liquid critical point (20), the terminal point of a line of first-order liquid–liquid phase transitions. According to one current hypothesis, the liquid–liquid critical point is the thermodynamic source of all water's anomalies (20–23). This region has been called the “no-man's land” because to date no experiments have been able to make direct measurements on the bulk liquid phase (21). Recently, the fragility transition in confined water was studied experimentally (24–26) because nucleation can be avoided in confined geometries. Also, a dynamic crossover has been associated with the liquid–liquid phase transition in silicon and silica (27, 28). In this work, we offer an interpretation of the dynamic crossover (called a fragility transition or fragile–strong transition by many authors) in water as arising from crossing the Widom line emanating from the hypothesized liquid–liquid critical point (27) (Fig. 1c, path α). Our thermodynamic and structural interpretation of the dynamic crossover may not hold for liquids for which the fragile–strong dynamic crossover can be caused by other mechanisms, as discussed in ref. 29.
Methods
Using molecular dynamics simulations, we study three models, each of which has a liquid–liquid critical point. Two of the models, [the TIP5P (30) and the ST2 (31)] treat the water molecule as a multiple-site rigid body, interacting via electrostatic site–site interactions complemented by a Lennard–Jones potential. The third model is the spherical “two-scale” Jagla potential with attractive and repulsive ramps (Fig. 2), which has been studied in the context of liquid–liquid phase transitions and liquid anomalies (16, 32). For all three models, we evaluate the loci of maxima of the relevant response functions, compressibility and specific heat, that coincide close to the critical point and give rise to the Widom line. We provide evidence that, for all three potentials, a dynamic crossover occurs when the Widom line is crossed.
Fig. 2.
The two-scale Jagla ramp potential with attractive and repulsive ramps. Here UR = 3.5U0, UA = – U0, a is the hard-core diameter, b = 1.72a is the soft-core diameter, and c = 3a is the long-distance cutoff. In the simulation, we use a as the unit of length and U0 as the unit of energy.
Our results for the TIP5P potential are based on molecular dynamics simulations of a system of n = 512 molecules, carried out in both the NPT and NVT ensembles by using the techniques described in ref. 33. For ST2 simulations n = 1,728 molecules are used, and all of the simulations are carried out in NVT ensemble. For the Jagla potential, a discrete molecular dynamics simulation (32) implemented for n = 1,728 particles interacting with step potentials (34) is used in both NVT and NVE ensembles. (For these ensembles, N denotes particle number, P denotes pressure, T denotes temperature, V denotes volume, and E denotes energy.)
Results
Fig. 3a shows for TIP5P the relevant portion of the P–T phase diagram. A liquid–liquid critical point is observed (33, 35), from which the Widom line develops. The coexistence curve is negatively sloped, so the Clapeyron equation implies that the high-temperature phase is a high-density liquid (HDL), and the low-temperature phase is a low-density liquid (LDL). Fig. 3b shows the T dependence of the diffusion coefficient D, evaluated from the long time limit of the mean square displacement along isobars. The isobars crossing the Widom line (Fig. 3c, path α) show a clear crossover from a non-Arrhenius behavior at high T [which can be well fit by a power law function D ∼ (T – TMCT)γ], consistent with the mode coupling theory (MCT) predictions (36), to an Arrhenius behavior at low T [which can be described by D ∼ exp(–Ea/RT)], where R is the gas constant. The crossover between these two functional forms takes place when crossing the Widom line.
Fig. 3.
Results for the TIP5P potential. (a) Relevant part of the phase diagram, showing the liquid–liquid critical point C at Pc ≈ 320 MPa and Tc ≈ 217 K, the line of isobaric specific heat maxima 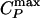 , and the line of isothermal compressibility maxima
, and the line of isothermal compressibility maxima 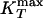 .(b) Arrhenius plot of the diffusion constant D as a function of 1,000/T along different isobars. The filled circles indicate the temperatures at which the
.(b) Arrhenius plot of the diffusion constant D as a function of 1,000/T along different isobars. The filled circles indicate the temperatures at which the 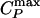 line is crossed. (c) Arrhenius plot of D as a function of 1,000/T for P = 100 MPa (path α). At high temperatures, D can be fit by D ∼ (T – TMCT)γ (dashed line, also shown in Inset), where TMCT ≈ 231 K and γ ≈ 1.9. At low temperatures, the dynamic behavior changes to that of a liquid where D is Arrhenius (solid line). (d) Log–log plot of D as a function of T – TMCT for P = 400 MPa (path β). The behavior of D remains non-Arrhenius for the entire temperature range and is consistent with D ∼ (T – TMCT)γ, with TMCT ≈ 201 K and γ ≈ 2.5. Note that the power law fits for γ and TMCT are subject to error due to the relatively small ranges of D and T – TMCT.
line is crossed. (c) Arrhenius plot of D as a function of 1,000/T for P = 100 MPa (path α). At high temperatures, D can be fit by D ∼ (T – TMCT)γ (dashed line, also shown in Inset), where TMCT ≈ 231 K and γ ≈ 1.9. At low temperatures, the dynamic behavior changes to that of a liquid where D is Arrhenius (solid line). (d) Log–log plot of D as a function of T – TMCT for P = 400 MPa (path β). The behavior of D remains non-Arrhenius for the entire temperature range and is consistent with D ∼ (T – TMCT)γ, with TMCT ≈ 201 K and γ ≈ 2.5. Note that the power law fits for γ and TMCT are subject to error due to the relatively small ranges of D and T – TMCT.
For paths β (Fig. 3d), crystallization occurs in TIP5P (33), so the hypothesis that there is no fragility transition cannot be checked at low temperature. Hence we consider a related potential, ST2, for which crystallization is absent within the time scale of the simulation. Simulation details are described in ref. 37. This potential also displays a liquid–liquid critical point (20, 37), as seen in the phase diagram of Fig. 4a. The analog of Fig. 3b is shown in Fig. 4b. We confirm that along paths α, a dynamic crossover takes place (Fig. 4c). Moreover, along paths β, the T dependence of D does not show any sign of crossover to Arrhenius behavior, and the fragile behavior is retained down to the lowest studied temperature (note that 103/T extends to 4.8 K–1). Indeed, for paths β, the entire T dependence can be fit by a power law (T – TMCT)γ (Fig. 4c).
Fig. 4.
Analog of Fig. 3 for the ST2 potential. (a) Relevant part of the phase diagram, showing the liquid–liquid critical point C at Pc ≈ 186 MPa and Tc ≈ 246 K, the line of isobaric specific heat maxima 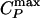 , the line of isothermal compressibility maxima
, the line of isothermal compressibility maxima 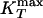 , and the spinodal lines. (b) Arrhenius plot of the diffusion constant D as a function of 1,000/T along different isobars. The filled circles indicate the temperatures at which the
, and the spinodal lines. (b) Arrhenius plot of the diffusion constant D as a function of 1,000/T along different isobars. The filled circles indicate the temperatures at which the 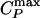 line is crossed. (c) Arrhenius plot of D as a function of 1,000/T for P = 0 MPa (path α). At high temperatures, D can be fit by D ∼ (T – TMCT)γ (dashed line, also shown in Inset) where TMCT ≈ 268 K and γ ≈ 1.34. At low temperatures, the dynamic behavior changes to that of a liquid where D is Arrhenius (solid line). (d) Log–log plot of D as a function of T – TMCT for P = 200 MPa (path β). The behavior of D remains non-Arrhenius for the entire temperature range and is consistent with D ∼ (T – TMCT)γ, with TMCT ≈ 217 K and γ ≈ 1.7. Note that the power law fits for γ and TMCT are subject to error due to the relatively small ranges of D and T – TMCT.
line is crossed. (c) Arrhenius plot of D as a function of 1,000/T for P = 0 MPa (path α). At high temperatures, D can be fit by D ∼ (T – TMCT)γ (dashed line, also shown in Inset) where TMCT ≈ 268 K and γ ≈ 1.34. At low temperatures, the dynamic behavior changes to that of a liquid where D is Arrhenius (solid line). (d) Log–log plot of D as a function of T – TMCT for P = 200 MPa (path β). The behavior of D remains non-Arrhenius for the entire temperature range and is consistent with D ∼ (T – TMCT)γ, with TMCT ≈ 217 K and γ ≈ 1.7. Note that the power law fits for γ and TMCT are subject to error due to the relatively small ranges of D and T – TMCT.
Thus, we see that the simulations for both TIP5P and ST2 water models support the connection between the Widom line and the fragile–strong transition. It is natural to ask which features of the water molecular potential are responsible for the properties of water discussed here, especially because water's unusual properties are shared by several other liquids whose intermolecular potential has two energy (length) scales (28, 27). We next investigate the two-scale spherically symmetric Jagla potential. The Jagla model displays (without the need to supercool) a liquid–liquid coexistence line that, unlike water, has a positive slope, implying that the Widom line is now crossed along α paths with P > Pc (Figs. 1d and 5a). There is a crossover in the behavior of D(T) when the 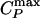 line is crossed (Fig. 5 b and c). At high temperature, D exhibits an Arrhenius behavior (Fig. 5 b and c), whereas at low temperature it follows a non-Arrhenius behavior, consistent with a power law. Along a β path (P < Pc), D(T) follows the Arrhenius behavior over the entire studied temperature range (Fig. 5 b and d). Thus, the dynamic crossover coincides with the location of the
line is crossed (Fig. 5 b and c). At high temperature, D exhibits an Arrhenius behavior (Fig. 5 b and c), whereas at low temperature it follows a non-Arrhenius behavior, consistent with a power law. Along a β path (P < Pc), D(T) follows the Arrhenius behavior over the entire studied temperature range (Fig. 5 b and d). Thus, the dynamic crossover coincides with the location of the 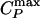 line, extending the conclusion of the TIP5P and ST2 potentials to a general two-scale spherically symmetric potential.
line, extending the conclusion of the TIP5P and ST2 potentials to a general two-scale spherically symmetric potential.
Fig. 5.
Analog of Figs. 3 and 4 for the two-scale Jagla potential. (a) Phase diagram in the vicinity of the liquid–liquid critical point C located at Pc ≈ 0.24 and Tc ≈ 0.37, the line of isobaric specific heat maxima 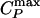 , the line of isothermal compressibility maxima
, the line of isothermal compressibility maxima 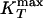 , and the spinodal lines. (b) The T dependence of diffusivity along constant pressure paths. Several paths α and paths β are shown. (i) P = 0.175, 0.200, 0.225 < Pc (paths β in Fig. 1d, along which the system remains in the LDL phase). (ii) P = 0.250, 0.275, 0.30 > Pc (paths α in Fig. 1d, along which the system does not remain in the LDL-like state, but the dynamic behavior changes from Arrhenius to non-Arrhenius). (c) D as a function of 1/T for P = 0.250 (path α). At high temperatures, the fit is Arrhenius D ∼ exp(–1.59/T) (solid line), whereas at low temperatures, the results are consistent with D ∼ (T – TMCT)γ with TMCT ≈ 0.27 and γ ≈ 2.7 (dashed line, also shown in Inset). (d) For P = 0.225 (path β), D is Arrhenius for the entire temperature range and can be fit by D ∼ exp(–1.62/T). The unit of D is a
, and the spinodal lines. (b) The T dependence of diffusivity along constant pressure paths. Several paths α and paths β are shown. (i) P = 0.175, 0.200, 0.225 < Pc (paths β in Fig. 1d, along which the system remains in the LDL phase). (ii) P = 0.250, 0.275, 0.30 > Pc (paths α in Fig. 1d, along which the system does not remain in the LDL-like state, but the dynamic behavior changes from Arrhenius to non-Arrhenius). (c) D as a function of 1/T for P = 0.250 (path α). At high temperatures, the fit is Arrhenius D ∼ exp(–1.59/T) (solid line), whereas at low temperatures, the results are consistent with D ∼ (T – TMCT)γ with TMCT ≈ 0.27 and γ ≈ 2.7 (dashed line, also shown in Inset). (d) For P = 0.225 (path β), D is Arrhenius for the entire temperature range and can be fit by D ∼ exp(–1.62/T). The unit of D is a 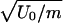 , and the unit of P is U0/a3.
, and the unit of P is U0/a3.
Discussion and Summary
Before concluding, we note that our findings are consistent with the possibility that the observed dynamic crossover along path α is related to the behavior of CP, suggesting that enthalpy or entropy fluctuations may have a strong influence on the dynamic properties. The role of CP is consistent with expectations based on the Adams–Gibbs (38) interpretation of the water dynamics (39, 40) and of the fragility transition (10, 27).
For both water and the Jagla model, crossing the Widom line is associated with a change in the T dependence of the dynamics. In the case of water, D(T) changes from non-Arrhenius (“fragile”) to Arrhenius (“strong”) behavior, whereas the structural and thermodynamic properties change from those of HDL to those of LDL. For the Jagla potential, because of the positive slope of the Widom line, D(T) changes from Arrhenius to non-Arrhenius, whereas the structural and thermodynamic properties change from those of LDL to those of HDL.
In summary, our results for water are consistent with the experimental observation in confined water of (i) a fragility transition for P < Pc (25, 26), and (ii) a peak in CP upon cooling water at atmospheric pressure (41). Thus, our work offers a plausible interpretation of the results of ref. 26, consistent with the existence of a liquid–liquid critical point located in the no-man's land.
Acknowledgments
We thank C. A. Angell, G. Franzese, K. Koga, J. M. H. Levelt Sengers, L. Liu, M. Mazza, S. Sastry, F. W. Starr, H. Tanaka, B. Widom, and Z. Yan for helpful discussions and National Science Foundation Grant CHE 0096892 and Ministero dell'Istruzione, dell'Università e della Ricerca–Fondo per gli Investimenti della Ricerca di Base (MIUR-FIRB) for support. We thank D. Chandler and J. P. Garrahan for helpful criticisms on the manuscript. We also thank the Boston University Computation Center, Yeshiva University, and St. Francis Xavier University hpcLAB (high-performance computing laboratory) for allocation of CPU time.
Author contributions: L.X., P.K., S.V.B., S.-H.C., P.H.P., F.S., and H.E.S. designed research, performed research, and wrote the paper.
Abbreviations: MCT, mode coupling theory; LDL, low-density liquid; HDL, high-density liquid.
References
- 1.Debenedetti, P. G. (1996) Metastable Liquids: Concepts and Principles (Princeton Univ. Press, Princeton).
- 2.Levelt, J. M. H. (1958) Ph.D. Thesis (Univ. of Amsterdam, Van Gorkum & Co., Assen, The Netherlands).
- 3.Michels, A., Levelt, J. M. H. & Wolkers, G. (1958) Physica 24, 769–794. [Google Scholar]
- 4.Michels, A., Levelt, J. M. H. & de Graaff, W. (1958) Physica 24, 659–671. [Google Scholar]
- 5.Anisimov, M. A., Sengers, J. V. & Levelt Sengers, J. M. H. (2004) in Aqueous System at Elevated Temperatures and Pressures: Physical Chemistry in Water, Stream, and Hydrothermal Solutions, eds. Palmer, D. A., Fernandez-Prini, R. & Harvey, A. H. (Elsevier, Amsterdam), pp. 29–71.
- 6.Robinson, G. W., Zhu, S.-B., Singh, S. & Evans, M. W. (1996) Water in Biology, Chemistry, and Physics: Experimental Overviews and Computational Methodologies (World Scientific, Singapore).
- 7.Bellissent-Funel, M.-C., ed. (1999) Hydration Processes in Biology: Theoretical and Experimental Approaches (IOS Press, Amsterdam).
- 8.Angell, C. A. (1993) J. Phys. Chem. 97, 6339–6341. [Google Scholar]
- 9.Debenedetti, P. G. (2003) J. Phys. Condens. Matter 15, R1669–R1726. [Google Scholar]
- 10.Starr, F. W., Angell, C. A. & Stanley, H. E. (2003) Physica A 323, 51–66. [Google Scholar]
- 11.Angell, C. A. (2004) Ann. Rev. Phys. Chem. 55, 559–583. [DOI] [PubMed] [Google Scholar]
- 12.Horbach, J. & Kob, W. (1999) Phys. Rev. B 60, 3169–3181. [Google Scholar]
- 13.Prielmeier, F. X., Lang, E. W., Speedy, R. J. & Lüdemann, H. D. (1987) Phys. Rev. Lett. 59, 1128–1131. [DOI] [PubMed] [Google Scholar]
- 14.Lang, E. W. & Lüdemann, H. D. (2004) Angew Chem. Intl. Ed. Engl. 21, 315–329. [Google Scholar]
- 15.Ito, K., Moynihan, C. T. & Angell, C. A. (1999) Nature 398, 492–495. [Google Scholar]
- 16.Jagla, E. A. (1999) J. Chem. Phys. 111, 8980–8986. [Google Scholar]
- 17.Jagla, E. A. (1999) J. Phys. Condens. Matter 11, 10251–10258. [Google Scholar]
- 18.Jagla, E. A. (2001) Phys. Rev. E 63, 061509. [DOI] [PubMed] [Google Scholar]
- 19.Tanaka, H. (2003) J. Phys. Condens. Matter 15, L703–L711. [Google Scholar]
- 20.Poole, P. H., Sciortino, F., Essmann, U. & Stanley, H. E. (1992) Nature 360, 324–328. [Google Scholar]
- 21.Mishima, O. & Stanley, H. E. (1998) Nature 396, 329–335. [Google Scholar]
- 22.Franzese, G., Malescio, G., Skibinsky, A., Buldyrev, S. V. & Stanley, H. E. (2001) Nature 409, 692–695. [DOI] [PubMed] [Google Scholar]
- 23.Sciortino, F., La Nave, E. & Tartaglia, P. (2003) Phys. Rev. Lett. 91, 155701. [DOI] [PubMed] [Google Scholar]
- 24.Bergman, R. & Swenson, J. (2000) Nature 403, 283–286. [DOI] [PubMed] [Google Scholar]
- 25.Faraone, A., Liu, L., Mou, C.-Y., Yen, C.-W. & Chen, S.-H. (2004) J. Chem. Phys. 121, 10843–10846. [DOI] [PubMed] [Google Scholar]
- 26.Liu, L., Chen, S.-H., Faraone, A., Yen, C.-W. & Mou, C.-Y. (2005) Phys. Rev. Lett. 95, 117802. [DOI] [PubMed] [Google Scholar]
- 27.Saika-Voivod, I., Poole, P. H. & Sciortino, F. (2001) Nature 412, 514–517. [DOI] [PubMed] [Google Scholar]
- 28.Sastry, S. & Angell, C. A. (2003) Nat. Mater. 2, 739–743. [DOI] [PubMed] [Google Scholar]
- 29.Garrahan, J. P. & Chandler, D. C. (2003) Proc. Natl. Acad. Sci. USA 100, 9710–9714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Jorgensen, W. L. (1982) J. Chem. Phys. 77, 4156–4163. [Google Scholar]
- 31.Stillinger, F. H. & Rahman, A. (1972) J. Chem. Phys. 57, 1281–1292. [Google Scholar]
- 32.Kumar, P., Buldyrev, S. V., Sciortino, F., Zaccarelli, E. & Stanley, H. E. (2005) Phys. Rev. E 72, 021501. [DOI] [PubMed] [Google Scholar]
- 33.Yamada, M., Mossa, S., Stanley, H. E. & Sciortino, F. (2002) Phys. Rev. Lett. 88, 195701. [DOI] [PubMed] [Google Scholar]
- 34.Buldyrev, S. V. & Stanley, H. E. (2003) Physica A 330, 124–129. [Google Scholar]
- 35.Paschek, D. (2005) Phys. Rev. Lett. 94, 217802. [DOI] [PubMed] [Google Scholar]
- 36.Götze, W. (1991) in Liquids, Freezing, and Glass Transition, eds. Hansen, J. P., Levesque, D. & Zinn-Justin, J. (North–Holland, Amsterdam), pp. 287–503.
- 37.Poole, P. H., Saika-Voivod, I. & Sciortino, F. (2005) J. Phys. Condens. Matter 17, L431–L437. [DOI] [PubMed] [Google Scholar]
- 38.Adams, G. & Gibbs, J. H. (1965) J. Chem. Phys. 43, 139–146. [Google Scholar]
- 39.Angell, C. A., Finch, E. D., Woolf, L. A. & Bach, P. (1976) J. Chem. Phys. 65, 3063–3066. [Google Scholar]
- 40.Scala, A., Starr, F. W., La Nave, E., Sciortino, F. & Stanley, H. E. (2000) Nature 406, 166–169. [DOI] [PubMed] [Google Scholar]
- 41.Maruyama, S., Wakabayashi, K. & Oguni, M. (2004) Am. Inst. Phys. Conf. Proc. 708, 675–676. [Google Scholar]







