Energetics of nanocrystalline TiO₂

Abstract

The energetics of the TiO₂ polymorphs (rutile, anatase, and brookite) were studied by high temperature oxide melt drop solution calorimetry. Relative to bulk rutile, bulk brookite is 0.71 ± 0.38 kJ/mol (6) and bulk anatase is 2.61 ± 0.41 kJ/mol higher in enthalpy. The surface enthalpies of rutile, brookite, and anatase are 2.2 ± 0.2 J/m², 1.0 ± 0.2 J/m², and 0.4 ± 0.1 J/m², respectively. The closely balanced energetics directly confirm the crossover in stability of nanophase polymorphs inferred by Zhang and Banfield (7). An amorphous sample with surface area of 34,600 m²/mol is 24.25 ± 0.88 kJ/mol higher in enthalpy than bulk rutile.

Titania is an important accessory oxide mineral (1) and is used widely in technology (2–4). Rutile is the stable high temperature phase, but anatase and brookite are common in fine grained (nano-scale) natural and synthetic samples (5–7). On heating concomitant with coarsening, the following transformations are all seen, each under somewhat different conditions of particle size, starting material, temperature, and other parameters (refs. 4 and 7–9; Appendix Appendix): anatase to brookite to rutile, brookite to anatase to rutile, anatase to rutile, and brookite to rutile. These variable transformation sequences imply very closely balanced energetics as a function of particle size (10). It has been proposed that the surface enthalpies of the three polymorphs are sufficiently different that crossover in thermodynamic stability can occur under conditions that preclude coarsening, with anatase and/or brookite stable at small particle size (3, 7).

The energetics of anatase, brookite, and rutile were measured by high temperature oxide melt solution calorimetry, first by Navrotsky and Kleppa (5) and later by Mitsuhashi and Kleppa (6). Their results, as well as those of other studies (11–14), scatter significantly (Table 1 and Appendix B).

Table 1.

Reported enthalpies of transformation for TiO₂ polymorphs

ΔH, kJ/mol	Method	Reference
Rutile = anatase
−11.67	High P-T studies	11
−0.42	Tabulation	13
0.42 ± 0.21	Differential thermal analysis	12
2.61 ± 0.41	Oxide melt calorimetry, surface area considered	This work
2.93 ± 1.26	Differential scanning calorimetry	6
3.26 ± 0.84	Oxide melt calorimetry	6
6.57 ± 0.79	Oxide melt calorimetry	5
8.37 ± 5.92	Fluorine combustion calorimetry	14
Rutile = brookite
0.42 ± 0.31	Differential thermal analysis	12
0.71 ± 0.38	Oxide melt calorimetry	6
0.84 ± 0.42	Differential scanning calorimetry	6
41.84 ± 9.36	Fluorine combustion calorimetry	14

^*Unreasonable.

^† Recommended values.

Previously, using high temperature oxide melt calorimetry for nanocrystalline Al₂O₃, it was shown that γ- Al₂O₃ (the phase observed for nano-sized particles) is more stable in enthalpy than nanophase α-Al₂O₃ (corundum), the macrocrystalline thermodynamically stable phase (15, 16). The goal of this work is to gather calorimetric evidence concerning the analogous proposed phase stability reversal for nanocrystalline TiO₂. Such information is essential for understanding fundamental solid state chemistry, for predicting phase equilibria, for controlling nucleation, grain growth, and phase transformation, and thus is fundamental to technological applications. Energetics of anatase, brookite, and rutile have been measured by high-temperature oxide melt drop solution calorimetry at 975 K with 3Na₂O⋅4MoO₃ solvent, using a Calvet twin microcalorimeter. The effects of particle size and adsorbed water are considered.

Experimental Section

Synthesis.

Anatase NA1 was synthesized from (NH₄)₂Ti(OH)₂(C₃H₅O₃)₂ and cetyltrimethylammonium chloride (CTAC). A white precipitate was formed when water was added. Vigorous stirring readily dissolved it. Water addition and stirring was continued until irreversible precipitation occurred. The reaction was stirred first at room temperature overnight, then at 343 K for 24 h, and finally at 373 K for 48 h in a sealed Teflon reactor. The precipitate was washed and centrifuged several times with water. The sample was calcined at 623 K for 2 h in air to remove CTAC. Anatase–rutile samples NAR1–NAR6 were generated by heating NA1 for 4.5, 24, 48, 72, 144, and 240 h at 623 K.

Amorphous TiO₂ (AM) was synthesized by mixing titanium ethoxide with ethanol (17). The mixture was stirred at 273 K for 2 h. After dripping water (1.6 mol) that contained four drops of acetic acid, the mixture was aged for 0.5 h. The product was white and x-ray amorphous. Anatase samples NA2, NA3, and NA4 were obtained by heating AM for 3 h in air at 673 K, 771 K, and 748 K, respectively.

NR1 and NR2 nanorutile samples were synthesized by using a sol-gel method (18). Solutions of TiCl₃ and NH₄OH were mixed in the volume ratio 1:6 and 1:3, respectively. The initial pH was 0.1, which slowly increased to 2. The mixture was stirred for 48 h at 300 K. The precipitate was centrifuged and washed with isopropyl alcohol and dried at room temperature to obtain nanorutile. To make NR3, titanium isopropoxide and dry isopropyl alcohol were added dropwise to a well stirred solution of nitric acid (pH, 0.5; ref. 18). The sample was stirred for 8 h. Isopropyl alcohol was evaporated at 355 K. The sample was transferred to a Teflon container and heated in a titanium autoclave at 523 K for 26 h under continuous stirring. The powder was dried.

Pure nanophase brookite NB was synthesized as described (19, 20). Titanium isopropoxide was mixed with distilled water in a beaker and stirred at room temperature for 1 h. The suspension was vacuum filtered and washed with distilled water, ensuring that the precipitate remained wet. This paste was added to an appropriate amount of NaOH in an autoclave and heated at 423 K for 14 days. The autoclave was cooled for a day and the precipitate was collected, filtered, washed with distilled water, and dried.

Bulk rutile (99.995% metals basis) dried at 973 K overnight was used to complete the thermochemical cycles.

Characterization.

X-ray diffraction patterns (XRD) were collected by using a Scintag (Santa Clara, CA) PAD V diffractometer (Cu Kα, 45 kV, 40 mA, θ-2θ goniometer geometry) with a step size of 0.02° and collection time of 10 s per step (without an internal standard). The specific surface area was measured by using the Brunauer–Emmett–Teller (BET) technique with a Gemini 2360 instrument (Micromeritics, Norcross, GA). For electron microprobe analysis, a Cameca (Paris) SX-50 instrument was used. Carbon content was obtained from LECO (St. Joseph, MI). Water contents were determined by using weight loss measurements. TiO₂ samples, accurately weighed inside a glovebox, were heated for 12 h at 1,473 K. The products were white, implying negligible oxygen deficiency. The difference between the final weight and the initial weight gives the water content. The molar compositions (formula weights) were normalized to obtain 1 M of sample, x M of water, and y M of other impurities.

Calorimetry.

All moisture-sensitive nanocrystalline samples were handled in an argon-filled glovebox (O₂ and H₂O < 1 ppm). High temperature drop solution calorimetry in 3Na₂O⋅4MoO₃ solvent was performed in a custom-built Calvet twin microcalorimeter described in refs. 21 and 22. Oxygen gas was flushed through the glassware at ≈90 ml/min and bubbled through the solvent at ≈5 ml/min. This procedure maintains oxidizing conditions, helps remove evolved water, and agitates the solvent to aid dissolution. The samples were pressed into pellets (usually ≈15 mg) inside the glovebox, weighed, and stored in a glass vial. When a stable calorimeter baseline was obtained, the pellet from the glass vial was dropped into the calorimeter. The total time the pellet was exposed to the atmosphere was less than 10 s. For all samples, calibration was performed by using the heat content of corundum pellets of similar weight.

Results and Discussion

Sample Characterization.

XRD verified that the samples were single-phase (anatase NA1–NA4, rutile NR1–NR3, or brookite NB) and quantified the amounts of anatase and rutile in the two-phase mixtures, according to procedures similar to those of Zhang and Banfield (7).

In addition to water, nanocrystalline samples prepared by sol-gel methods may retain some organic impurities. In all of the nano TiO₂ samples, ≈0.1 wt % carbon was detected. We suspect this is physisorbed CO₂ resulting from exposure to air during the commercial chemical analysis and call it “atmospheric” carbon. We believe this was not present on the samples handled in the glovebox and used for calorimetry. A scan combining thermogravimetry, differential thermal analysis, and mass spectroscopy of calorimetric samples did not detect CO or CO₂. The “atmospheric” carbon was subtracted from the measured carbon content to determine the actual carbon content of the calorimetric samples.

In anatase–rutile mixtures, the major phase (> 95%) was anatase. XRD showed that when the particle size of anatase reached ≈13 nm, rutile began to form, as observed (3). Once formed, the rutile particles grew very rapidly. Thus, samples NAR1–NAR6 were mixtures of nanocrystalline anatase and rutile with rapidly increasing particle size. The specific surface area rapidly decreased, suggesting coarsening. The surface area and transformation enthalpy for the anatase–rutile mixtures are normalized to correct for rutile to obtain the variation of enthalpy of pure anatase with surface area (see footnote in Table 2). Because rutile coarsens more rapidly than anatase, we used the enthalpy of bulk rutile for this correction. This effect does not introduce significant error because the amount of rutile is small (<5%). The difference between particle sizes estimated by XRD and BET suggests considerable agglomeration of nanoparticles (Table 2).

Table 2.

Sample characterization and thermochemical data

Sample	Composition	Wt % C	Particle size XRD, nm	Surface area BET, m2/mol and m2/g	Particle size calculated from BET, nm	ΔHds (measured), kJ/mol	ΔHds (corrected), kJ/mol	ΔHtrans, kJ/mol
Rutile	Alfa Aesar Puratronic TiO2			>1000		57.95  ± 0.71 (23)	57.95  ± 0.71 (23)
NA1	Anatase, 0.027 H2O	0.143	10.4	11985 (150)	10.4	50.73  ± 0.65 (8)	50.93  ± 0.65	7.02  ± 0.96
NA2	Anatase, 0.1606 H2O	0.086	7.2	9588 (120)	13.0	60.49  ± 0.60 (5)	49.41  ± 0.60	8.54  ± 0.93
NA3	Anatase, 0.03283 H2O	0.039	24.2	3036 (38)	41.1	59.05  ± 0.42 (6)	56.79  ± 0.42	1.16  ± 0.82
NA4	Anatase, 0.07308 H2O	0.067	13.5	5273 (66)	23.7	59.04  ± 0.39 (5)	53.99  ± 0.39	3.95  ± 0.81
NAR1	0.018 Rutile, 0.982 anatase, 0.05883 H2O	0.049	13.1 (A)	5193 (65)	24.0	55.43  ± 0.44 (6)	51.37  ± 0.44	6.58  ± 0.83
			23.8 (R)	5289 (66)			6.70  ± 0.83
NAR2	0.048 Rutile, 0.952 anatase, 0.04446 H2O	0.042	16.0 (A)	4235 (53)	29.4	56.53  ± 0.49 (6)	53.46  ± 0.49	4.48  ± 0.87
			19.0 (R)	4448 (56)			4.71  ± 0.87
NAR3	0.045 Rutile, 0.955 anatase, 0.04428 H2O	0.039	20.4 (A)	3436 (43)	36.3	58.03  ± 0.57 (6)	54.97  ± 0.57	2.98  ± 0.91
			48.4 (R)	3598 (45)			3.12  ± 0.91
NAR4	0.040 Rutile, 0.960 anatase, 0.01612 H2O	0.042	22.2 (A)	479 (6)	259.8	55.26  ± 0.39 (6)	54.15  ± 0.39	3.80  ± 0.81
			41.1 (R)	499 (6)			3.96  ± 0.81
NAR5	0.036 Rutile, 0.964 anatase, 0.01707 H2O	0.050	24.4 (A)	399 (5)	312.0	56.26  ± 0.29 (6)	55.08  ± 0.29	2.87  ± 0.77
			>100.0 (R)	414 (5)			2.97  ± 0.77
NAR6	0.051 Rutile, 0.949 anatase, 0.01500 H2O	0.128	23.9 (A)	399 (5)	310.9	55.64  ± 0.33 (6)	54.61  ± 0.33	3.34  ± 0.78
			63.3 (R)	421 (5)			3.52  ± 0.78
NR1	Rutile, 0.23473 H2O	0.087	8.0	5833 (73)	19.3	61.54  ± 0.73 (7)	45.15  ± 0.73	12.76  ± 1.01
NR2	Rutile, 0.06613 H2O	0.052	12.0	4554 (57)	24.7	53.54  ± 0.58 (6)	48.98  ± 0.58	8.97  ± 0.91
NR3	Rutile, 0.08316 H2O	—	22.0	1758 (22)	64.0	57.77  ± 0.24 (4)	52.03  ± 0.24	5.92  ± 0.75
NB	Brookite, 0.1219 H2O, 8.325e-3 Na2CO3	0.210	23.0	6392 (80)	18.0	60.36  ± 0.63 (10)	50.84  ± 0.88	7.11  ± 1.13
AM	Amorphous, 0.03283 H2O, 0.0404 C	0.422	—	34596 (433)	—	58.34  ± 0.53 (6)	33.69  ± 0.53	24.25  ± 0.88

^*Values in parentheses are the experimentally obtained BET areas in m²/g.

^† Value is the mean of the number of experiments indicated in parentheses. Error is two standard deviations of the mean.

^‡ After correction for H₂O and other impurities.

^§ For reaction TiO₂ (rutile, bulk) = TiO₂ (polymorph, nano).

^¶ Normalized values of the surface area and transformation enthalpy for anatase-rutile mixtures (NAR1–NAR6). Calculations to obtain 100% anatase from these samples are as follows: x anatase ⋅ (1-x) rutile mixture with surface area A and transformation enthalpy H is normalized to 100% anatase with surface area of A/x and transformation enthalpy of H/x.

^**Not detected because of the limited amount of sample.

Thermochemistry.

Table 2 lists the enthalpies of drop solution. The enthalpy difference between a nanocrystalline sample and bulk rutile arises from polymorphism, surface energy, and presence of water and any other impurities. Correction for water, present in all nanocrystalline TiO₂ samples, is performed through a thermochemical cycle (Appendix Appendix). Because the weight loss observed by thermogravimetry occurs below 673 K, the water is assumed to be physisorbed and to have the enthalpy of bulk liquid water.

The carbon impurity in amorphous TiO₂ (AM) is assumed to be energetically equivalent to graphite (Appendix Appendix). The brookite sample (NB) also needs to be corrected for a sodium impurity—this is assumed to be Na₂CO₃ (Appendix Appendix). The difference between the corrected drop solution enthalpy of the nanocrystalline sample and bulk rutile is equal to the sum of the enthalpy due to polymorphism and surface enthalpy. It is called the transformation enthalpy and can be written, for example for anatase, as

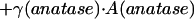where γ is the surface enthalpy and A is the surface area.

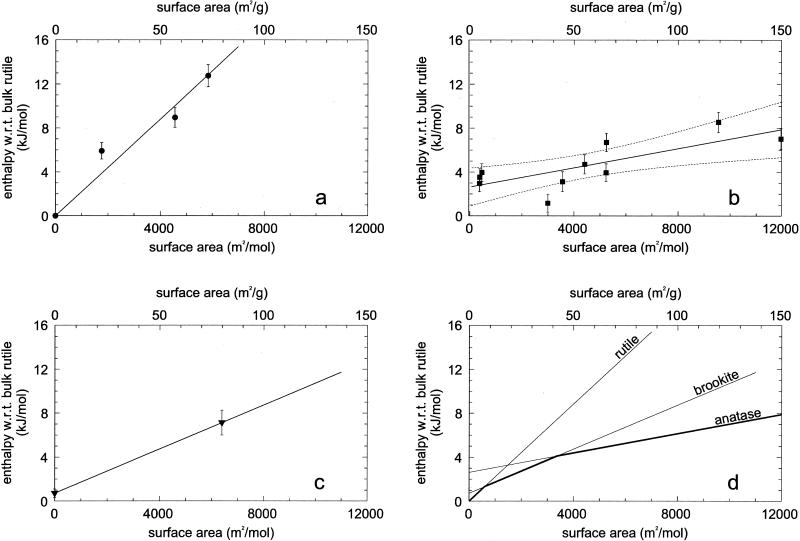
Fig. 1 shows the transformation enthalpies of nanocrystalline samples (kJ/mol) versus surface areas (m²/mol). A linear fit for each structure yields both the surface enthalpy (slope) and the bulk phase transformation enthalpy (intercept). Fig. 1a represents the enthalpy of nanorutile. Bulk rutile is taken as the reference point of zero enthalpy for all samples. A linear fit using these three nanorutile data are therefore forced through the origin to derive the surface enthalpy of nanocrystalline rutile as 2.2 ± 0.2 J/m². The uncertainty comes from the fitting program, but there are too few data points for more detailed statistical analysis.

Fig 1.

Enthalpy of nanocrystalline samples with respect to bulk rutile (kJ/mol) versus surface area (m²/mol) for nanorutile samples NR1–NR3 (a), for nanoanatase samples NA1–NA4 (b), and normalized nanoanatase–rutile mixtures NAR1–NAR6 (dashed curves represent 95% confidence limits for the mean) for nanobrookite sample NB and brookite–rutile phase transformation from Mitsuhashi and Kleppa (6) (c), and phase stability crossover of titania. The lines are taken from a–c and the darker line segments indicate the energetically stable phases (d).

Fig. 1b shows the anatase data (normalized to pure anatase as discussed above). A linear fit yields the surface enthalpy of anatase as 0.4 ± 0.1 J/m² and the enthalpy of phase transformation of bulk rutile to bulk anatase as 2.61 ± 0.41 kJ/mol. The uncertainty comes from the statistical fitting program, and the 95% confidence limits are shown in the figure.

Fig. 1c represents the enthalpy of the one nanocrystalline brookite (NB) and the bulk brookite–rutile phase transformation enthalpy (0.71 ± 0.38 kJ/mol) of Mitsuhashi and Kleppa (6). Attempts to obtain pure brookite of other surface areas, either by direct synthesis or by coarsening sample NB, were not successful. Therefore, the linear fit is constrained by only two points. It gives the surface enthalpy of brookite as 1.0 ± 0.2 J/m². This uncertainty is only an estimate.

Fig. 1d summarizes the enthalpy of nanocrystalline titania. The intersections of the linear fits of brookite and rutile and of brookite and anatase place a limit on the stability field of various polymorphs. Rutile is energetically stable for surface area <592 m²/mol (7 m²/g), brookite is energetically stable from 592 to 3,174 m²/mol (7–40 m²/g), and anatase is energetically stable for greater surface areas. The anatase and rutile energetics cross at 1,452 m²/mol (18 m²/g). The dark solid lines represent the phases of lowest enthalpy as a function of surface area. The energetic stability crossovers are confirmed. Assuming spherical particles, the calculated average diameters of rutile and brookite for 7 m²/g surface area are 201 nm and 206 nm, and of brookite and anatase for 40 m²/g surface area are 36 nm and 39 nm. These differences in particle size at the same surface area exist because of the difference in density of the phases. If the phase transformation takes place without further coarsening, the particle size should be smaller after the transformation. In practice, this effect has probably not been observed.

Of course phase stability in a thermodynamic sense is governed by the Gibbs free energy (ΔG = ΔH − TΔS) rather than the enthalpy. Low-temperature heat capacity and entropy data are available for anatase and rutile (6), but not for brookite. The data for anatase probably refer to a fine-grained (perhaps nanophase) sample, but no characterization is given. Thus the anatase entropy may contain contributions from both bulk and surface terms. The data suggest that rutile and anatase have the same entropy within experimental error [S⁰ (298 K, rutile) = 50.6 ± 0.6 J/mol⋅K and S⁰ (298 K, anatase) = 49.9 ± 0.3 J/mol⋅K (35)]. Thus the TΔS will not significantly perturb the sequence of stability seen from the enthalpies.

Amorphous TiO₂ with surface area of 34600 m²/mol was found to be 24.25 ± 0.88 kJ/mol higher in enthalpy than bulk rutile.

General Implications of Surface Enthalpies and Enthalpies of Phase Transformation.

Zhang and Banfield (7) reported the average surface enthalpies of rutile and anatase as 1.93 and 1.34 J/m², respectively, based on atomistic simulations. They estimated the surface enthalpy of brookite as 1.66 J/m². These theoretical values were consistent with the values of 0.5–1.7 J/m² estimated by differential scanning calorimetry by Terwilliger and Chiang (36). Vittadini et al. (37) used the generalized gradient approximations of density functional theory to calculate the energy of the anatase (101) and (001) surface as 0.52 and 0.81 J/m² and that of the rutile (110) surface as 0.82 J/m². This suggests that rutile has the highest surface enthalpy, brookite the intermediate, and anatase the lowest. The calorimetric surface enthalpies for rutile, brookite, and anatase, 2.2 ± 0.2, 1.0 ± 0.2, and 0.4 ± 0.1 J/m², respectively, agree with this sequence, although their numerical values are somewhat different. The theoretical calculations calculate energies for specific crystal faces. However, it is not known what factors, both thermodynamic and kinetic, control the development of various crystal faces in the nanocrystalline powders. The relative abundance of different surfaces, even for the same area, may vary for differently prepared samples. The surface enthalpies derived from the calorimetric data thus represent a direct determination of the surface enthalpy averaged for different crystal faces as they exist in real nanocrystalline samples. The scatter in the nanoanatase calorimetric data may reflect such differences rather than purely random statistical factors.

For nanocrystalline titania, the variable observed transformation sequence can be explained by using the enthalpy crossover (Fig. 1d). If the initially formed brookite has surface area >40 m²/g, it is metastable with respect to both anatase and rutile, and the sequence brookite to anatase to rutile during coarsening is energetically downhill. If anatase formed initially, it can coarsen and transform first to brookite (at 40 m²/g) and then to rutile. The energetic driving force for the latter reaction (brookite to rutile) is very small, explaining the natural persistence of coarse brookite. In contrast, the absence of coarse grained anatase is consistent with the much larger driving force for its transformation to rutile.

Abbreviations

• XRD, x-ray diffraction patterns

Appendix A: Brief Literature Review of Anatase–Brookite–Rutile Phase Transformation

Zhang and Banfield (3) and Gribb and Banfield (4) observed that the synthesis of ultrafine titania resulted in anatase and/or brookite, which on coarsening transformed to rutile after reaching a certain particle size. Once rutile was formed, it grew much faster than anatase. They analyzed the phase stability of anatase and rutile thermodynamically to conclude that anatase became more stable than rutile for particle size <14 nm. Hwu et al. (23) commented that whether TiO₂ was rutile or anatase depended on the preparation method. For small particle size (<50 nm) anatase seemed more stable and transformed to rutile at ≈973 K.

Zhang and Banfield (7) studied the phase transformation behavior of nanocrystalline aggregates during their growth for isothermal and isochronal reactions by using XRD. They suggested that transformation sequence and thermodynamic phase stability depend on the initial particle sizes of anatase and brookite. They concluded that, for equally sized particles, for particle size <11 nm, anatase was thermodynamically stable, for particle size between 11 nm and 35 nm, brookite was stable, and for particle size >35 nm, rutile was stable. They cautioned that, for real samples, the particle sizes of different phases were not equal, which could alter the direction of initial transformation. They concluded that the energetics of these polymorphs were sufficiently close that they could be reversed by small differences in surface energy.

Ye et al. (8) studied the thermal behavior of nanocrystalline brookite by using thermogravimetry, differential thermal analysis, and diffraction. They observed a slow brookite to anatase phase transition below 1,053 K along with grain growth. Between 1,053 K and 1,123 K, they noticed rapid brookite to anatase and anatase to rutile transformations. Above 1,123 K, they saw rapid grain growth of rutile, which became the dominant phase. They concluded that brookite cannot transform directly to rutile but has to transform to anatase first. Kominami et al. (9) observed that nanocrystals of brookite directly transformed to rutile above 973 K, in contrast to the observations of Ye et al.

Zhang et al. (24) measured micro-Raman spectra of nano-sized TiO₂ powders prepared by vapor hydrolysis. They obtained amorphous TiO₂ at 533 K and predominantly anatase at 873–1,173 K. The anatase–rutile transformation temperature depended on particle size and was complete at ≈1,323 K. They noted that the phase transformation of amorphous TiO₂ was a two-step process: amorphous to anatase followed by anatase to rutile. They proposed that the rutile formation started at the surface and migrated into the bulk. They also noted that the brookite impurities, detected by Raman spectroscopy but not by XRD, were present on the anatase surface.

Zhang and Banfield (25, 26) proposed that the mechanism of anatase–rutile phase transformation was temperature-dependent. They suggested this transformation was dominated by interface nucleation below 873 K, by both interface and surface nucleation at 893–1,273 K, and by bulk nucleation above 1,273 K.

The anatase–rutile transformation depends on impurities, grain size, reaction atmosphere, and synthesis conditions (26–31). Zhang and Banfield (26) reported that the anatase–rutile phase transformation occurred at higher temperature with the addition of Al₂O₃. They attributed this to suppression of coarsening caused by surface diffusion. Okada et al. (27) and Yoshinaka et al. (28) found that the anatase–rutile phase transformation occurred at higher temperature with the addition of SiO₂. Yang et al. (29) showed that synthesis conditions (chemicals/peptizing agents) affect the crystallinity and anatase–rutile phase transition temperature. Zaban et al. (30) noted that the surface structure of TiO₂ is affected by the preparation conditions. Ahonen et al. (31) studied the effect of gas atmospheres (nitrogen and air) and temperature on the crystal structure and specific surface area. They observed that anatase synthesized in air transformed to rutile at 973 K, whereas anatase synthesized in nitrogen persisted to 1,173 K. Gouma and Mills (32) studied the anatase–rutile phase transformation in commercial TiO₂ powders with an average particle size of 100 nm. Using transmission and scanning electron microscopy, they concentrated on the structural evolution (shape and morphology) of the particles. They proposed that rutile plates were formed initially by a shear force and subsequent coarsening involved interactions between the transforming particle and surrounding anatase particles.

Appendix B: Previous Studies of Transformation Enthalpies

B1 Rutile–Anatase.

Navrotsky and Kleppa (5) studied rutile–anatase phase transformation by using high-temperature oxide melt solution calorimetry. They obtained the enthalpy of phase transformation at 968 K as 6.57 ± 0.79 kJ/mol. They did not report the water contents, impurities, and particle size. They concluded that anatase was metastable with respect to rutile under all conditions of temperature and pressure.

Mitsuhashi and Kleppa (6) determined the enthalpy of the rutile–anatase phase transformation by using high-temperature oxide melt solution calorimetry and differential scanning calorimetry (DSC) to be 3.26 ± 0.84 kJ/mol and 2.93 ± 1.26 kJ/mol, respectively. The values from solution calorimetry and DSC agree. However, they did not specify the particle size for their hydrothermally prepared anatase. Zhang and Banfield (7) suggested that this sample is likely to be fairly coarse. Mitsuhashi and Kleppa (6) mentioned that the samples contained <0.7 wt % volatiles and ≈1–3 mol % other TiO₂ impurities, but they apparently did not correct the calorimetric results for the impurities. They suggested that the discrepancy between their results and earlier studies (5) might be due to incomplete dissolution in the earlier work. We believe that the difference in particle size may be the governing factor.

Rao (12) estimated the enthalpy of the rutile–anatase phase transformation at 1,176 K to be 0.42 ± 0.21 kJ/mol by DTA using spectroscopically pure anatase. The sample preparation was identical to that of Czanderna et al. (33). They reported a surface area of ≈40 m²/g (which corresponds to ≈40-nm-diameter particles).

Margrave and Kybett (14) reported a rutile–anatase transformation enthalpy of 8.37 ± 5.92 kJ/mol when using fluorine combustion calorimetry. Based on high-pressure–temperature phase data, Vahldiek (11) estimated the rutile–anatase transformation enthalpy as −11.67 kJ/mol. Robie and Waldbaum (13) tabulated the rutile–anatase phase transformation enthalpy as −0.42 kJ/mol.

B2 Rutile–Brookite.

Rao et al. (34) estimated the enthalpy of the rutile–brookite phase transformation as 0.42 ± 0.31 kJ/mol based on DTA experiments on a natural sample that contained ≈4 wt % impurities. Margrave and Kybett (14), using fluorine combustion, reported the rutile–brookite phase transformation enthalpy to be 41.84 ± 9.36 kJ/mol. This value seems unreasonably large. Mitsuhashi and Kleppa (6) synthesized brookite by hydrolysis of tetraisopropyl orthotitanate in an aqueous solution of 1 M NaF. They treated the precipitate hydrothermally for 48 h at 703 K and 1 kbar (1 bar = 100 kPa), washed with hot dilute HNO₃, and dried at 408 K. Oxide melt solution calorimetry gave the rutile–brookite transformation enthalpy as 0.71 ± 0.38 kJ/mol. In the same study, a DSC experiment on a natural brookite sample (with unspecified impurity content) gave the transformation enthalpy as 0.84 ± 0.42 kJ/mol. The authors noted difficulties in using the natural sample for reliable solution calorimetry because of its impurity content and in using the synthesized sample for DSC experiments because of baseline problems resulting from shrinkage of the sample. However, they concluded that the magnitude of the enthalpy for transformation was well established and suggested that the value derived from solution calorimetry should be used. Both their samples are likely to be relatively coarse.

Appendix C: Thermochemical Cycles

C1 Thermochemical cycle to calculate the enthalpy from bulk rutile to pure anatase, pure rutile, and anatase–rutile mixtures.

C2 Thermochemical cycle to calculate the enthalpy of bulk rutile–amorphous TiO₂ (with C impurities assuming impurities behave as mechanical additions, see text).

C3 Thermochemical cycle to calculate the enthalpy of bulk rutile–brookite (with Na₂CO₃ impurities assuming impurities behave as mechanical additions, see text).