Self-organization in leaky threshold systems: The influence of near-mean field dynamics and its implications for earthquakes, neurobiology, and forecasting

Abstract

Threshold systems are known to be some of the most important nonlinear self-organizing systems in nature, including networks of earthquake faults, neural networks, superconductors and semiconductors, and the World Wide Web, as well as political, social, and ecological systems. All of these systems have dynamics that are strongly correlated in space and time, and all typically display a multiplicity of spatial and temporal scales. Here we discuss the physics of self-organization in earthquake threshold systems at two distinct scales: (i) The “microscopic” laboratory scale, in which consideration of results from simulations leads to dynamical equations that can be used to derive the results obtained from sliding friction experiments, and (ii) the “macroscopic” earthquake fault-system scale, in which the physics of strongly correlated earthquake fault systems can be understood by using time-dependent state vectors defined in a Hilbert space of eigenstates, similar in many respects to the mathematics of quantum mechanics. In all of these systems, long-range interactions induce the existence of locally ergodic dynamics. The existence of dissipative effects leads to the appearance of a “leaky threshold” dynamics, equivalent to a new scaling field that controls the size of nucleation events relative to the size of background fluctuations. At the macroscopic earthquake fault-system scale, these ideas show considerable promise as a means of forecasting future earthquake activity.

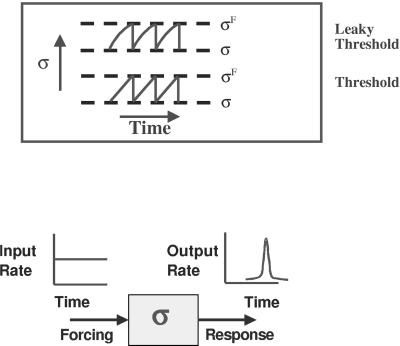
Driven nonlinear threshold systems are composed of interacting spatial networks of nonlinear “cells,” each having (i) one or more inputs, (ii) an internal state variable σ(t) that evolves in time in response to inputs, and (iii) one or more outputs. In general, the inputs and outputs of a cell are connected to other cells by a network of interactions and to an external source for σ. Threshold dynamics arises when a cell is subjected to a persistent external forcing that increases the value of σ through time until a predefined state threshold σ^F is reached, at which the cell “fires” or “fails,” thereby reducing σ to a residual value σ^R (Fig. 1). Thresholds, residual stresses, and internal states may be modified by the presence of quenched disorder, and the dynamics also may be modified by the presence of noise or annealed disorder. Interactions between cells, which lead to dynamical self-organization in these systems, may be excitatory (positive) in the sense that failure of connected neighbors brings a cell closer to firing, or inhibiting (negative) in the opposite case. Examples of such systems include earthquakes (1–3), neural networks (4, 5), depinning transitions in charge density waves and superconductors (6), magnetized domains in ferromagnets (7), avalanches in sandpiles (8), and domain rearrangements in flowing foams (9).

Fig 1.

Behavior of the state variable σ of a generic threshold unit as a function of time under a constant load rate. Both leaky (α > 0) and nonleaky (α = 0) behavior is shown. (Upper) State σ vs. time. (Lower) Rate of change of state vs. time.

In recent years, earthquakes and frictional sliding have emerged as the paradigm of self-organizing driven threshold systems. Beginning with the Burridge–Knopoff (BK) slider block model (10), simulation studies of driven threshold systems have been carried out in which each threshold “cell” is represented by a block sliding on a frictional surface. Physically, these blocks represent the sticking points, or asperities, on the fault surface. All blocks are connected to a loader plate by a spring having spring constant K_L. In addition, each block is connected to q other blocks by coupling springs, each spring having constant K_C/q. Thus the network of coupling springs represents the network of inputs and outputs. For these models, the state variable σ represents the shear stress that builds up until the static friction stress reaches the failure threshold σ^F. Sliding of each block commences at the threshold and continues until the block stress is reduced to the kinetic friction stress σ^R. During the sliding process, stress is transmitted from the sliding block(s) to other blocks by coupling springs. Because the BK model represents a planar fault, all interblock interactions are exciting, meaning that K_C > 0 (inhibiting interactions would have K_C < 0). Sliding of a given block then increases the stress on other blocks to which it is coupled, and therefore an avalanche of failing blocks may be initiated by a single unstable block. The avalanche of failing blocks represents an earthquake in the model. Whereas the original BK model specified massive blocks with inertial dynamics, recent models are more commonly of the stochastic cellular automaton type (11, 12), in which the sliding block travels a distance (σ − σ^R)/K + W, where K = K_L + K_C, and W is a random number representing random overshoot or undershoot during the sliding process (13).

We are particularly interested in the physics of self-organizing processes in mean field threshold systems (13–16), which in the case of the slider block model is described by the condition qK_C → ∞. In the mean field regime, the range of interaction becomes large, leading to damping of the fluctuations and the appearance of a mean field spinodal, the classical limit of stability of a spatially extended system (17, 18). Examined in this limit, driven threshold systems appear to be locally ergodic and display equilibrium behavior when driven at a uniform rate. After the initial discovery in 1995 (13) that driven mean field slider block systems with microscopic noise display equilibrium properties, other studies have confirmed local ergodicity and the existence of Boltzmann fluctuations in these and other systems (14, 16, 19–23). Thus the origin of the physics of scaling, critical phenomena, and nucleation appears to lie in the ergodic properties of these mean field systems. Further studies have shown that mean field and near-mean field systems are also associated with the appearance of an energy landscape (16, 24), similar to other equilibrium systems (25).

To summarize our results: The observable properties of self-organizing, strongly correlated, near-mean field-driven threshold systems arise from the underlying locally ergodic dynamics. The corresponding appearance of a mean field spinodal leads to a general coarse-grained equation for the dynamics of leaky threshold systems that applies, for example, to both earthquake fault systems and neural networks, with appropriate definitions of the various terms. At the laboratory (“microscopic”) scale, we can use these ideas to predict the form of the sliding friction equations that have been empirically observed in a number of laboratory studies. At the (“macroscopic”) field scale, we can also use these ideas to formulate methods that show considerable promise for earthquake forecasting and prediction. The self-organizing dynamics on the energy landscapes in these systems thus arises from the strong correlations and mean field nature of the physics.

Spinodal Equations

Consider the d = 2 mean field slider block system described above, in which each block is connected to q other blocks with springs having constants K_C/q. Each block is also connected to a loader plate translating at an externally imposed load velocity V by a spring with constant K_L. The coarse-grained dynamical equation is (16):

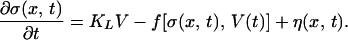As described in refs. 14–16, σ(x, t) is the coarse-grained stress within a volume of q blocks centered at x, and time is coarse-grained over a temporal window centered at t whose duration is roughly a few tenths of percent of the time interval between slips for an average block. It can be seen that Eq. 1 expresses the balance between the rate K_LV at which stress is accumulated at x by the loader plate motion and the rate f(σ(x, t), V) at which stress is dissipated by the sliding blocks. η(x, t) is a stochastic noise term. Denoting the spatial average over the sliding surface by 〈 〉, we define 〈σ(x, t)〉 = σ(t). Note that the sliding velocity of blocks across the surface is u(x, t), with spatial average u(t) = 〈u(x, t)〉 = ∂ 〈s(x, t)〉/∂t = ds(t)/dt, where s(x, t) is the coarse-grained slip on the surface at (x, t), and in general, u ≠ V. f(σ(x, t), V) is a general functional of {σ(x, t), V} that depends also on σ^F, σ^R, as well as on a thermalizing noise amplitude β. In view of the equations described in ref. 16, we expect a rather weak dependence of f(σ(x, t), V(t)) on V. Indeed, laboratory experiments at both the atomic (26) and the laboratory scale (27–33) indicate a dependence of stress σ ∼log V.

Mean Field and Thermodynamics

For the most part, we are interested here in modeling laboratory experiments carried out on elastically stiff, strongly correlated samples that are often viewed as lumped parameters. Thus we take qK_C → ∞ (16) and in addition use an equation describing the elasticity of the loader springs:

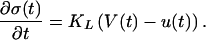In the mean field limit, the noise term is suppressed in Eq. 1, which then becomes:

Combining Eqs. 2 and 3, we obtain:

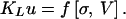Eq. 4 can be viewed as a thermodynamic equation of state for the contact zone. In the laboratory experiments on rate-and-state friction discussed below, the contact zone is defined as the volume of the sample that is spanned by the displacement gauges.

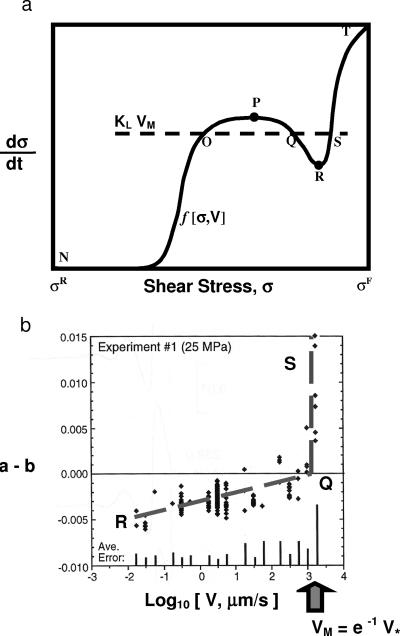
Fig. 2a is an illustration of generic example of f(σ, V), assuming steady-state conditions V = constant, and small noise level β⁻¹ (“low temperature”). The letters O, Q, S define the intersection of K_LV with the curve f(σ, V). f(σ, V) has the typical Van der Waals loop structure, in which there are two extrema (spinodals), indicated by the dots at P and R. In this particular case, the Maxwell velocity V_M is shown (dashed line), corresponding to the rate of stress supply K_LV_M that defines the two equal areas OPQ and QRS. The steady-state solution to Eq. 3 can be obtained graphically from Fig. 2a as the intersection of the line labeled K_LV with the curve f(σ, V) (which in this case is actually f(σ, V_M). It can be seen that there are three possible solutions: (i) a low-stress region having positive slope from N to P associated with either a stable or metastable phase; (ii) an intermediate stress region having negative slope from P to R that is always associated with an unstable phase; and (iii) a high-stress region having positive slope from R to T that is associated with either a stable or metastable phase. At low values of V < V_M, the branch NO would be stable, whereas the branch ST would be metastable. At high values of V > V_M, the branch NO would be metastable, whereas the branch ST would be stable. Observing the high-stress phase as the stable phase is difficult, but it can be seen under the proper conditions (34).

Fig 2.

(a) Schematic plot of the stress dissipation function f(σ, V) as a function of σ. Location of spinodals is indicated by filled circles. Maxwell velocity V_M (dashed horizontal line) corresponds to the stress supply rate K_LV_M at which the Area(OPQ) = Area(QRS). (b) Plot of a–b vs. Log ₁₀(V), where (a–b) = (A–B)/(normal stress). Data (diamonds) is from figure 5 of ref. 30, an experiment where the normal stress = 25 MPa. Dashed line labeled RQ is from Eq. 28 and corresponds to the path RQ in a. Dashed line labeled QS corresponds to the jump QS to the stable branch ST of a.

Leaky Threshold Equation

The leaky threshold equation for a single sliding block is obtained by expanding f(σ(t), V(t)) as a power series in σ(t), setting V = constant, and parameterizing the threshold instability by a Dirac δ function. Thus we have:

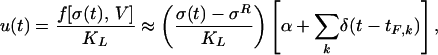where t_F,k is any of the k times defined by the condition σ(t_F,k) = σ^F. When α = 0, one has a pure, sharp threshold equation. The presence of nonzero α means, in the case of friction, that there exists stable aseismic slip preceding the instability at t = t_F. Such slip has often been observed in laboratory friction experiments (Fig. 1), modifying the sawtooth form of the data for stress plotted against slip, to produce a concave-down curvature (29). An equation of this type was first proposed in ref. 35 to describe the dynamics of an integrate-and-fire neuron. In that system, electric current replaces the stress variable.

Under the action of the leaky dynamics in Eq. 5, we can show that variations in stress in a slider block system are progressively reduced (stress-smoothing) if α > 0, and progressively increased (stress-roughening) if α < 0. Consider two slider blocks, connected to each other by a coupling spring K_C, and each connected to the loader plate by means of a loader spring K_L. Denoting the slip and stress of block 1 by s₁, σ₁, the equations for block 1 are then:

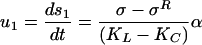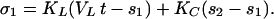An analogous set of equations holds for block 2. If the difference in stress at time t = 0 is given by δσ(0) = σ₂(0) − σ₁(0), then at a time t later:

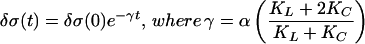From Eq. 5, it can be seen that α is a thermodynamic derivative:

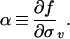The slope α of the f–σ curve determines whether stress smoothing or stress roughening occurs under the leaky dynamics. For general three-dimensional fault network models, both stress smoothing and stress roughening should occur, as well as the possibility of smoothing-to-roughening transitions. Data from laboratory experiments on sliding granite (29) indicate that α ∼ 0.1/T_R, where T_R is the recurrence interval for unstable slip.

Rate-and-State Equations

Using the general form of the single block, mean field equation K_L u = f(σ(t), V(t)) in Eq. 4, we can derive the general form of rate-and-state (rate–state) friction equations observed in laboratory experiments (27–33) and put a clear physical meaning to the various terms in the equations. In these experiments, a very stiff frictional apparatus drives sliding across a contact zone of thickness H between two rough surfaces. The elastic stiffness of the machine K_mach → ∞ allows us to assume that the load velocity V can be exactly prescribed, and that the measured stress in the elastic column σ_E is the same as the friction stress, thus σ = σ_E. The state of slip across the contact zone is monitored by a strain gauge, which is connected to a servomechanism to ensure that K_mach → ∞. In these experiments, the load velocity is suddenly stepped from V₁ to V, and the evolution of the friction stress σ is observed to change according to (28, 29):

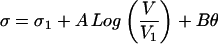The parameters A, B, and L₁ are determined by empirical fits to the laboratory data. L₁ is the only parameter with a clear physical interpretation; it is a length scale over which the stress evolves from σ₁ to σ after the velocity step. θ is a “state variable,” whose physical meaning is controversial (27–33).

It is known that Eqs. 10 and 11 are strictly accurate only for small velocity steps, |(V − V₁)/V₁| < 1, and that A is relatively independent of velocity, but that B itself depends on velocity (30), B ∼ Log V. Data also indicate that with increase in stress, (A–B), changes sign from negative to positive determined by a characteristic load velocity V. In this context, negative (A–B) means decreasing stress with increasing V, whereas positive (A–B) means increasing stress with increasing V.

As described above, the rate-and-state laboratory experiments are usually conducted by using a servomechanism that keeps the sliding from becoming unstable during sliding, so that the block will not “run away” during from the load apparatus. During these experiments, stress decreases as velocity increases. Referring to Fig. 2a, this means that the laboratory experiments (Fig. 2b) are exploring the branch R to Q in Fig. 2a. As the experiments continue to higher V, stress begins to increase dramatically as V increases. These experiments must therefore correspond to a jump from the branch RQ to the branch ST at the Maxwell velocity V_M described earlier.

To derive the first of the rate-and-state Eq. 10, we use the equation of state 4, K_L u = f(σ, V), and explicitly assume that u = V = constant. The assumption u = V is almost always made in analyzing laboratory experiments (27–33). By using this assumption and considering two velocities V and V_*, without further loss of generality we may write:

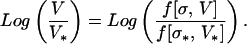Now expand the right-hand side about (σ_*, V_*):

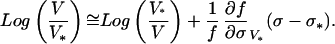We define a length scale L_*:

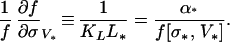The last equality follows from Eq. 9. In this form, it can be seen that L_* has the physical interpretation of being the shear offset across the contact zone at velocity V_* and stress σ_*, so that u(t) = dL(t)/dt = ds(t)/dt. Similarly, K_L is interpreted as the shear stiffness across the contact zone. Then for V near V_*:

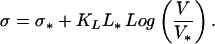Eq. 15 can be generalized to any velocity V if we allow L_* to be an arbitrary function of V, L_* → L = L(V):

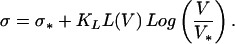We have, for example:

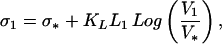valid for V₁ near V near V_*, and L₁ near L near L_*. Combining Eqs. 16 and 17 and neglecting second-order terms, we find:

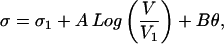as in Eq. 10, the first of the rate-and-state equations. Here, A ≡ K_LL₁, B ≡ −K_L L₁ Log(V/V_*), θ ≡ − ΔL/L₁,and ΔL ≡ L − L₁.

To recover the second of the rate-and-state equations (Eq. 11), we now allow small amplitude changes in u, thus u ≠ V. Thus the second rate–state equation represents a small-amplitude “correction” to the first equation. This latter result is well known in the literature (28–33), and as a consequence most experimentalists assume that a family of state variables θ_i is needed to adequately parameterize the data over finite ranges in V.

Starting from the equation of state (Eq. 4), we have:

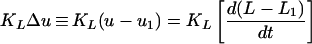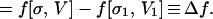Because f(σ, V) is a thermodynamic state function, it has an exact differential (36):

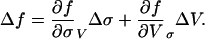Eq. 2 implies that at constant load velocity V:

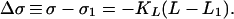The partial derivatives in Eq. 20 are:

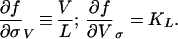The first of Eq. 22 follows from Eq. 14, with L_* replaced by L, and the fact that in steady state, V = u = constant. The second of Eq. 22 follows from Eq. 3. Combining Eqs. 19–22, we find:

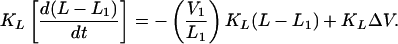If conditions are such that:

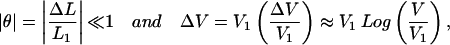then we can multiply Eq. 23 by −1/L₁, use the definitions below Eq. 18, and find:

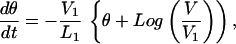which is the second of the rate-and-state equations and identical to Eq. 11.

Because we now know the origin and identity of the empirical parameters A, B, L₁, θ, we can put numerical values to the more physically meaningful parameters K_L, L, and V_M (also V_*) from the laboratory data that have been collected (30, 33). The quantity L₁ ∼ L ∼ L_* (see Eq. 24) is known to play the role of a relaxation length scale for θ and therefore σ, as can be seen from Eqs. 18 and 25. For experiments of granitic rock sliding on granitic rock, data from figure 4 of ref. 30 indicate that L₁ ∼ 10 μm. Alternatively, data from other experiments (33) finds L₁ ∼ 30 μm. To determine the value of K_L and V_*, we use laboratory data plotting (A–B) vs. Log V (Fig. 2b):

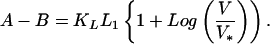According to Eq. 26, the plot of (A–B) vs. Log V is found to be a straight line, whose y intercept is K_LL₁(1 −Log V_*), whose slope is K_L L₁, and whose value for V_* is determined by the zero-crossing:

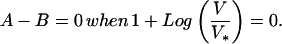Fig. 2b plots data from ref. 30, together with predictions from Eq. 26, the dashed line RQ that corresponds to the branch RQ of f(σ, V) in Fig. 2a. In addition, the dashed line QS is shown in Fig. 2b as well, corresponding to the jump from Q to S in Fig. 2a as V increases from below V < V_M to V > V_M. Note that (a–b) is plotted rather than (A–B), where (a–b) = (A–B)/(Normal Stress = 25 MPa). The dashed lines represent the data reasonably well and indicate that K_L ∼ 0.0025 MPa/μm for L₁ ∼ 10 μm. For comparison, the value for the machine stiffness K_mach = 0.048 MPa/μm (30), thus K_mach ≫ K_L. The transition from the unstable branch RQ in Fig. 2a to the stable branch ST must occur at V = V_M. From Eq. 27, V_M = e⁻¹ V_*, so by using Fig. 2b, we find V_M ∼ 1.26 mm/s and V_* = 3.42 mm/s.

General Equations for Earthquakes and Neural Networks

Hopfield (35) proposed a model for a network of N integrate-and-fire neurons. The dynamical equation for the kth neuron can be written as:

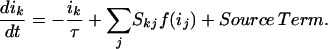Here i_k represents the electrical current entering the kth neuron; τ is a relaxation time; S_kj are the strengths of the synaptic connection weights for input from the jth neuron into the kth neuron; f(i_j) is the firing rate for spike-like action potentials from the jth neuron; and the “Source Term” represents a sensory driving term. Eq. 28 is based on the Hodgekin–Huxley model for neurodynamics and represents the same kind of mean field limit that has been examined here in connection with earthquakes.

In fact, the same equation (Eq. 28) is easily shown to describe the coarse-grained near-mean field limit for earthquake dynamics with appropriate redefinition of terms. Thus in place of “neurons,” we refer to “blocks” or “coarse-grained segments” of a fault (refer to Eqs. 1–5 above). Then i_k is replaced in Eq. 28 by the shear stress difference Δσ = σ_k − σ^R on the kth block or fault segment; τ = 1/α is a relaxation time; S_kj is replaced by the elastic interaction matrix T_kj; f(i_j) is replaced by either a series of spike-like functions δ(t − t_F), or more generally by the stress dissipation function f(σ_j, V) for the jth block or fault segment; and the “Source Term” is the plate driving stress K_LV. Because both systems have long-range interactions and therefore approach mean field conditions, we are led to expect that earthquake dynamics and neurodynamics should have many similar features and should be analyzed within similar mathematical frameworks.

Phase Dynamics at Macroscopic Scales

Self-organization processes in threshold systems occur at the macroscopic scale as well as at laboratory and atomic scales. The strong space–time correlations that are responsible for the cooperative behavior of these systems arise from the threshold dynamics as well as from the mean field (long-range) nature of the interactions. As we have described elsewhere (37–39), driven threshold systems can be considered examples of pure phase dynamical systems (40) when the rate of driving is constant, so that the integrated stress dissipation or firing rate over all sites is nearly constant, with the exception of small fluctuations:

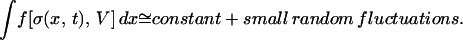The “constant” in Eq. 29 is the integral of the driving stress K_L V over all active faults within the volume, so that on average, the rate of stress dissipation is equal to the rate of stress supply. In threshold systems such as earthquake faults, the stress is typically supplied at a steady rate but is dissipated episodically by means of the earthquakes. Because of the mean field nature of both the simulated and real threshold systems, it is found that as the size of the system is increased, the amplitude of the “small fluctuations” decreases roughly as 1/√N.

By using both simulations and observed earthquake data (37–39), we showed elsewhere that the space–time patterns of threshold firings or earthquakes can be represented by a time-dependent system state vector in a Hilbert space. The length of the state vector represents the temporal frequency of events throughout the region and is closely related to the rate f(σ, V) at which stress is dissipated. In light of Eq. 29, it can be deduced that the information about the system state is represented solely by the phase angle of the state vector, hence the term “phase dynamics.” Changes in the norm of the state vector therefore represent only random Boltzmann-type fluctuations and can essentially be removed by requiring the system state vector to have a constant norm.

By using these ideas, we analyzed data from southern California since 1932 (refs. 38, 41; http://www.scecdc.scec.org/) between 32° and 37° north latitude and 238° and 245° east longitude. We tile the surface area with 3,162, d = two-dimensional boxes of scale size L_CG = 0.1° ∼ 11 km, corresponding roughly to the linear scale size of a magnitude m ∼ 6 earthquake. Of the 3,162 boxes, about N ≈2,000 contain at least one earthquake. We use the standard online data set available through the web site maintained by the Southern California Earthquake Center (http://www.scecdc.scec.org/), which consists of a record of all instrumentally recorded earthquakes beginning in January 1932 extending to the present. For this region, m_c = 3 is typically used to ensure catalog completeness since 1932. The idea is to use information on small events having scale λ < L_CG to forecast the occurrence of large events having scale λ > L_CG. For such a lattice of boxes (37, 39), a set of N physically meaningful, complete, orthonormal basis vectors ϕ_n(x_i) can be constructed. Physically, the ϕ_n(x_i) represent spatial patterns of earthquake activity defined on the N spatial boxes. The ϕ_n(x_i) are eigenvectors (“eigenpatterns”) of an N × N correlation operator. For example (37), define n(x_i, t) to be the activity rate (number of earthquakes/time) within the box centered at x_i at time t. From n(x_i, t), compute the mean-zero univariant time series z(x_i, t). The correlation operator K(x_i,x_j) is obtained by crosscorrelating z(x_i, t) with z(x_j, t). Diagonalizing K(x_i, x_j) produces the eigenfunctions ϕ_n(x_i).

From the time series of earthquake activity n(x_i, t), we compute (38, 41) the mean change Δs(x_i, t₁, t₂) in system state vector s(x_i, t) between two times, t₁ and t₂. Note that both Δs(x_i, t₁, t₂) and s(x_i, t) are defined in a coordinate system of a function space in which the ϕ_n(x_i) represent the coordinate axes. The physical picture is that Ŝ(x_i, t_b, t) is a unit vector in a Hilbert space that records present activity, so Δs(x_i, t₁, t₂) is proportional to a mean drift angle, or vector difference, that “points” in the “direction” of future patterns of activity. This picture is qualitatively similar to that for a scalar function f(t), in which Δf = {df(t)/dt} Δt is used to project future changes in f during a time interval Δt. The “direction” in which Δs(x_i, t₁, t₂) “points” has physical meaning because the ϕ_n(x_i) have physical meaning, in terms of spatial eigenpatterns of earthquake activity.

In a Hilbert space, sums or differences of state vectors represent probability amplitudes, allowing us to compute the probability for present and future activity. Because we are interested in the increase of probability above the time-dependent background probability μ_B(t₁, t₂), we first compute:

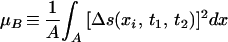The change in probability ΔP(x_i, t₁, t₂) for activity above the background is then:

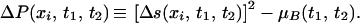We note that there are no free parameters in the computation of ΔP(x_i, t₁, t₂) to be determined by fits to data (no free “model parameters”).

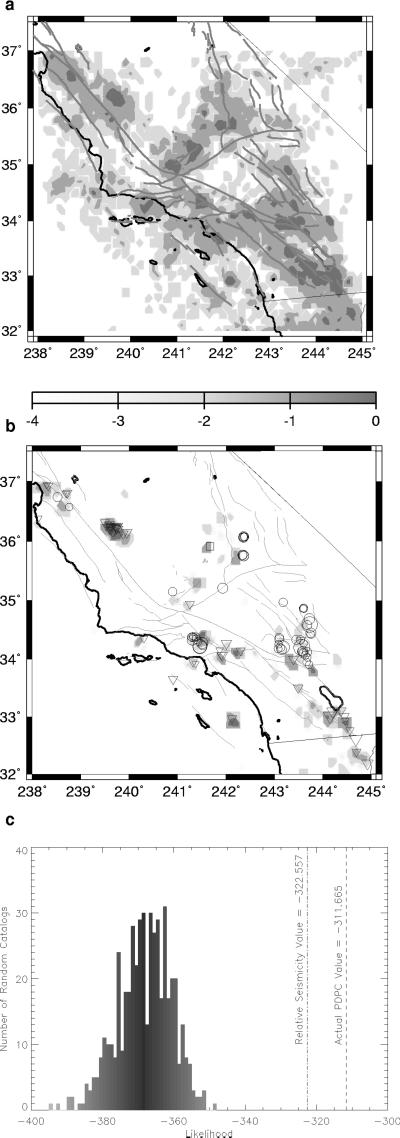
The intensity of seismic activity over the years 1932–1991 is shown in Fig. 3a. Fig. 3b is a shaded contour plot of Log₁₀ ΔP(x_i, t₁, t₂), ΔP(x_i, t₁, t₂) > 0, where t₁ = 01/01/1978, and t₂ = 12/31/1991. Shaded anomalies are associated with “large” (m ≥ 5.0) events for “current” (inverted triangles, t₁ < t < t₂) and future (circles, t₂ < t) time periods. No data were used in the shaded anomalies of Fig. 3b from the time after December 31, 1991, 6 months prior to the June 27, 1992 (moment magnitude) m ∼ 7.3 Landers (14) earthquake (34° 13′ N Lat., 116° 26′ W Long.).

Fig 3.

(a) Relative seismic intensity in southern California for the period 1932–December 31, 1991, plotted with linear shading scale. (b) Shaded-contour plot of Log₁₀ΔP(x_i, t₁, t₂), for locations at which ΔP(x_i, t₁, t₂) > 0. Times t₁ = January 1, 1978, and t₂ = December 31, 1991. Values are scaled by the maximum and shading scale is linear. Inverted triangles are events that occurred from 1978 to 1991 with 5 < m < 6 (smallest triangles); 6 < m < 7 (intermediate triangles); 7 < m (largest triangles). Circles are events that occurred from 1992 to the present, with 5 < m < 6 (smallest circles); 6 < m < 7 (intermediate circles); 7 < m (largest circles). (c) Log₁₀(ℒ) plots for 500 random catalogs (histogram), for the seismic intensity map of a (dash–dot line), and for the forecast in b (dashed line). All three methods were scored by the Likelihood test according to how well they forecast the events of magnitude m > 6 that occurred on or after January 1, 1992 (circles).

Visual inspection of Fig. 3b shows that the method has forecast skill, but rigorous statistical testing is needed. We used two types of null hypotheses to test the forecast in Fig. 3b. (i) We constructed thousands of random earthquake catalogs from the observed catalog by using the same total number of events, but assigning occurrence times from a uniform probability distribution over the years 1932–1991, and distributing them uniformly over the original locations. This procedure produces a Poisson distribution of events in space with an exponential distribution of inter-event times. Randomizing the catalog in this way destroys whatever coherent space–time structure may have existed in the data. These random catalogs are used to construct a set of null hypotheses, because any forecast method using such a catalog cannot, by definition, produce useful information. (ii) For the second null hypothesis, we used the seismic intensity data in Fig. 3a directly as a probability density at x_i, as has been proposed in the literature (43) for the “standard null hypothesis.”

We carried out a Maximum Likelihood test (41, 42, 45) to evaluate the accuracy with which our probability measure ΔP(x_i, t₁, t₂) can forecast “future” (t > t₂) “large” (m ≥ 5.0) events, relative to forecasts from the null hypotheses. Define 𝒫(x) to be the union of a set of N Gaussian density functions 𝓅_𝒢(|x −x_i|) (46) centered at each location x_i. Each elementary Gaussian density 𝓅_𝒢(|x −x_i|) has a peak value ΔP(x_i, t₁, t₂) + μ_B(t₁, t₂), the probability change including the background, if ΔP(x_i, t₁, t₂) > 0; a peak value μ_B(t₁, t₂) if ΔP(x_i, t₁, t₂) ≤ 0; as well as a standard deviation σ = L ∼ 11 km. 𝒫(x(e_j)) is then a probability measure that a future large event e_j occurs at location x(e_j). If there are J future large events, the likelihood ℒ that all J events are forecast is: 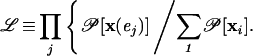In Fig. 3c, we show computations of (i) Log ₁₀(ℒ) for 500 random catalogs of the first type (histogram); (ii) Log ₁₀(ℒ) for the seismic intensity map in Fig. 1a (vertical dash–dot line); and (iii) Log ₁₀(ℒ) for our forecast of Fig. 3b (dashed line). Because larger values of Log ₁₀(ℒ) indicate a more successful hypothesis, we conclude that our method has forecast skill.

Implications

The diffusive mean field nature of the dynamics leads to several important predictions. First, forecasts such as those shown in Fig. 3b that are computed from changes over a time interval Δt = t₂ − t₁ should convey information for times t approximately in the range: t₂ < t < t₂ + Δt. That is, the time interval Δt during which the changes occur should be roughly the time interval Δt after t₂ for which the forecast is valid. Second, anomalies of elevated probability having area Ω should persist for a characteristic time τ ∝ Ω^η, where η ∼ 1 (41). Finally, the dynamics implies that we can compute probabilities using path integral methods (41), an approach that we are currently formulating.

Earthquake Forecasts

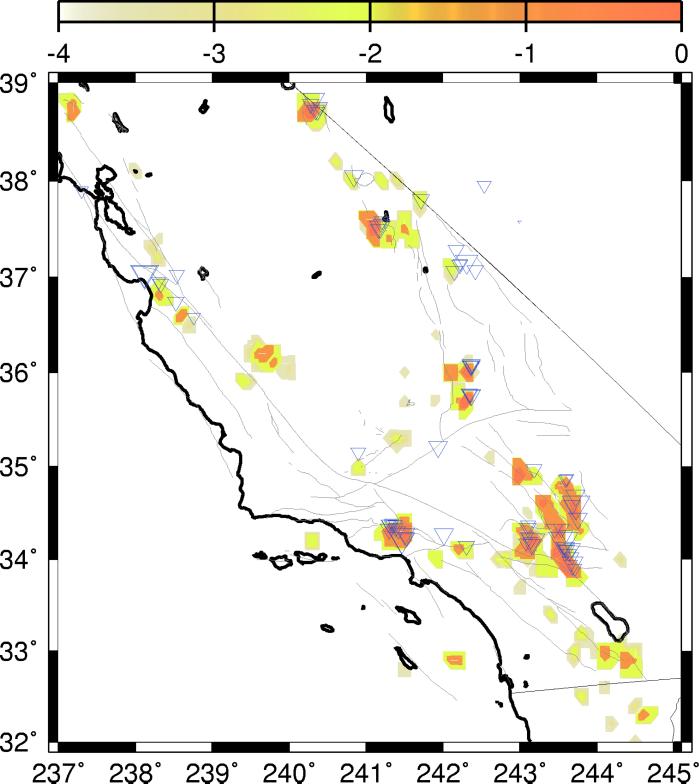
The most unbiased test possible is to use our method to forecast future activity into the 21st century, because we do not have knowledge of the future. Fig. 4 shows such a forecast for future large events following roughly the period ∼2000–2010, based on changes during the years 1989–1999. As seen from Fig. 3, the shaded anomalies appear to be sensitive to locations of events as small as m ∼ 5, even though the horizontal resolution of the boxes was chosen to correspond to events with magnitudes m > 6. Although at this stage of the research subjective judgments must still be made in the interpretation of the information in Fig. 4, we feel that a few broad statements can be made.

Fig 4.

Shaded contour plot of Log₁₀ΔP(x_i, t₁, t₂) for locations at which ΔP(x_i, t₁, t₂) > 0. Times t₁ = January 1, 1989, and t₂ = December 31, 1999. Inverted triangles are events during 1989–1999.

Specifically, on the basis of the area and intensity of the anomalies and the absence of events during 1989–1999 falling on the peak of the anomaly, Fig. 4 calls attention to areas that seem to be at risk for larger earthquakes having m > 5 during 2000–2010. The areas seemingly most at risk in central and southern California include the region north of Bishop [37.6° latitude (Lat.), 241.5° longitude (Long.)]; the Coso–Ridgecrest area (36.0° Lat., 242.1° Long. and 35.7° Lat., 242.1° Long.); the Coalinga area (36.1° Lat., 239.6° Long.); the Barstow area (34.9° Lat., 243° Long.); the area north of the 1992 Landers earthquake (34.5° Lat., 243.3° Long.); the area northwest of Palm Springs (34.0° Lat., 243.3° Long.); the Oceanside area (33.0° Lat., 117.9° 242.1 Long.); the Superstition Hills area (33.0° Lat., 1244.1° Long.); and the Imperial Valley (33.0° Lat., 244.4° Long.). On the basis of previous history and the intensity and area of the anomalies, some of these locations may be at risk for earthquakes with magnitudes approaching m ∼ 7, for example in the Imperial Valley, near Coalinga, and north of Landers.

Summary—Self-Organization Across Many Scales of Space and Time

Driven mean field threshold systems can develop strong correlations as a result of interactions. When both mean field interactions and a source of microscopic noise or chaos are present to act as a thermalizing influence, these systems demonstrate locally ergodic behavior. They can be analyzed by using the methods of statistical mechanics. In frictional systems and earthquakes, the most physically meaningful object is the stress dissipation function f(σ, V). As we have discussed, K_L u = f(σ, V) behaves as an equation of state for a frictional contact zone, and it also provides the physical basis for computing the system state vector for earthquake activity. On the “microscopic” scale of laboratory experiments, the form of f(σ, V), together with the scaling properties of these systems, is the signature of the self-organizing processes that are observed in the data. These processes lead to distinct scaling exponents, the rate-and-state frictional equations, and other data. On the “macroscopic” scale of regional earthquake fault systems, self-organization leads to the appearance of phase dynamics and a state vector whose rotations characterize the evolution of earthquake activity in the system. The origin of the phase-dynamical behavior of the system is a result of the balance between the average rate at which stress is supplied and the average rate at which it is dissipated, which is characterized by f(σ, V). Further understanding of the physics embodied in the stress dissipation function f(σ, V) would therefore seem to be critical to understanding the self-organization and related processes across the many scales of space and time that characterize the dynamics of earthquakes and other similar driven mean field threshold systems. In particular, because of the considerable similarities in the equations for earthquakes and neural networks, we expect the same conclusions to hold for neurodynamics as well.