Predictability of catastrophic events: Material rupture, earthquakes, turbulence, financial crashes, and human birth

Abstract

We propose that catastrophic events are “outliers” with statistically different properties than the rest of the population and result from mechanisms involving amplifying critical cascades. We describe a unifying approach for modeling and predicting these catastrophic events or “ruptures,” that is, sudden transitions from a quiescent state to a crisis. Such ruptures involve interactions between structures at many different scales. Applications and the potential for prediction are discussed in relation to the rupture of composite materials, great earthquakes, turbulence, and abrupt changes of weather regimes, financial crashes, and human parturition (birth). Future improvements will involve combining ideas and tools from statistical physics and artificial/computational intelligence, to identify and classify possible universal structures that occur at different scales, and to develop application-specific methodologies to use these structures for prediction of the “crises” known to arise in each application of interest. We live on a planet and in a society with intermittent dynamics rather than a state of equilibrium, and so there is a growing and urgent need to sensitize students and citizens to the importance and impacts of ruptures in their multiple forms.

What do a high-pressure tank on a rocket, a seismic fault, and a busy market have in common? Recent research suggests they can all be described in much the same basic physical terms—as self-organizing systems that develop similar patterns over many scales, from the very small to the very large. All three have the potential for extreme behavior: rupture, quake, or crash.

Similar characteristics are exhibited by other crises that often present fundamental societal impacts and range from large natural catastrophes, such as volcanic eruptions, hurricanes and tornadoes, landslides, avalanches, lightning strikes, catastrophic events of environmental degradation, to the failure of engineering structures, social unrest leading to large-scale strikes and upheaval, economic drawdowns on national and global scales, regional power blackouts, traffic gridlock, diseases and epidemics, etc. Intense attention and efforts are devoted in the academic community, in government agencies, and in the industries that are sensitive to or directly interested in these risks, to the understanding, assessment, mitigation, and if possible, prediction of these events.

A central property of such complex systems is the possible occurrence of coherent large-scale collective behaviors with a very rich structure, resulting from the repeated nonlinear interactions among its constituents: the whole turns out to be much more than the sum of its parts. It is widely believed that most complex systems are not amenable to mathematical analytic descriptions and can be explored only by means of “numerical experiments.” In the context of the mathematics of algorithmic complexity (1), many complex systems are said to be computationally irreducible, i.e., the only way to decide about their evolution is to actually let them evolve in time. Accordingly, the “dynamical” future time evolution of complex systems would be inherently unpredictable. This unpredictability does not prevent, however, the application of the scientific method for the prediction of novel phenomena as exemplified by many famous cases (prediction of the planet Neptune by Leverrier from calculations of perturbations in the orbit of Uranus, the prediction by Einstein of the deviation of light by the sun's gravitation field, the prediction of the helical structure of the DNA molecule by Watson and Crick based on earlier predictions by Pauling and Bragg, etc.). In contrast, this unpredictability refers to the frustration to satisfy the quest for the knowledge of what tomorrow will be made of, often filled by the vision of “prophets” who have historically inspired or terrified the masses.

The view that complex systems are inherently unpredictable has recently been defended persuasively in concrete prediction applications, such as the socially important issue of earthquake prediction (see the contributions in ref. 2). In addition to the persistent failures to find a reliable earthquake predictive scheme, this view is rooted theoretically in the analogy between earthquakes and self-organized criticality (3, 4). In this “fractal” framework, there is no characteristic scale, and the power law distribution of earthquake sizes reflects the fact that large earthquakes are nothing but small earthquakes that did not stop. They are thus unpredictable because their nucleation is not different from that of the multitude of small earthquakes, which obviously cannot be all predicted (5).

Is it really impossible to predict all features of complex systems? Take our personal life. We are not really interested in knowing in advance at what time we will go to a given store or drive on a highway. We are much more interested in forecasting the major bifurcations ahead of us, involving the few important things, like health, love, and work, which account for our happiness. Similarly, predicting the detailed evolution of complex systems has no real value and that we are taught that it is out of reach from a fundamental point of view does not exclude the more interesting possibility of predicting phases of evolutions of complex systems that really count, like the extreme events.

It turns out that most complex systems in the natural and social sciences do exhibit rare and sudden transitions that occur over time intervals that are short compared with the characteristic time scales of their posterior evolution. Such extreme events express more than anything else the underlying “forces” usually hidden by an almost perfect balance and thus provide the potential for a better scientific understanding of complex systems.

It is essential to realize that the long-term behavior of these complex systems is often controlled in large part by these rare catastrophic events. The universe was probably born during an extreme explosion (the “big bang”). The nucleosynthesis of all important heavy atomic elements constituting our matter results from the colossal explosion of supernovae (those stars heavier than our sun whose internal nuclear combustion diverges at the end of their lives). The largest earthquake in California, which repeats about once every two centuries, accounts for a significant fraction of the total tectonic deformation. Landscapes are shaped more by the “millennium” flood that moves large boulders rather than by the action of all other eroding agents. The largest volcanic eruptions lead to major topographic changes as well as severe climatic disruptions. According to some contemporary views, evolution is probably characterized by phases of quasistasis interrupted by episodic bursts of activity and destruction (6, 7). Financial crashes, which can cost in an instant trillions of dollars, loom over and shape the psychological state of investors. Political crises and revolutions shape the long-term geopolitical landscape. Even our personal lives are shaped in the long run by a few key decisions or events.

The outstanding scientific question that needs to be addressed to guide prediction is how large-scale patterns of a catastrophic nature might evolve from a series of interactions on the smallest and increasingly larger scales, where the rules for the interactions are presumed identifiable and known. For instance, a typical report on an industrial catastrophe describes the improbable interplay among a succession of events. Each event has a small probability and limited impact in itself. However, their juxtaposition and chaining lead inexorably to the observed losses. A common denominator of the various examples of crises is that they emerge from a collective process: the repetitive actions of interactive nonlinear influences on many scales lead to a progressive build-up of large-scale correlations and ultimately to the crisis. In such systems, it has been found that the organization of spatial and temporal correlations does not stem, in general, from a nucleation phase diffusing across the system. It results rather from a progressive and more global cooperative process occurring over the whole system by repetitive interactions.

For hundreds of years, science has proceeded on the notion that things can always be understood—and can only be understood—by breaking them down into smaller pieces and by coming to know these pieces completely. Systems in critical states flout this principle. Important aspects of their behavior cannot be captured by knowing only the detailed properties of their component parts. The large-scale behavior is controlled by their cooperativity and scaling up of their interactions. This is the key idea underlying the four examples that illustrate this new approach to prediction: rupture of engineering structures, earthquakes, stock market crashes, and human parturition (birth).

Prediction of Rupture in Complex Systems

Nature of the Problem.

The damage and fracture of materials are technologically of major interest because of their economic and human costs. They cover a wide range of phenomena such as cracking of glass, aging of concrete, the failure of fiber networks, and the breaking of a metal bar subject to an external load. Failures of composite systems are of utmost importance in the naval, aeronautics, and space industries. By the term “composite,” we include both materials with contrasted microscopic structures and assemblages of macroscopic elements forming a superstructure. Chemical and nuclear plants suffer from cracking caused by corrosion of either chemical or radioactive origin, aided by thermal and/or mechanical stress. More exotic but no less interesting phenomena include the fracture of an old painting, the pattern formation of the cracks of drying mud in deserts, and rupture propagation in earthquake faults.

Despite the large amount of experimental data and the considerable effort that has been undertaken by material scientists, many questions about fracture and fatigue have not yet been answered. There is no comprehensive understanding of rupture phenomena, but only a partial classification in restricted and relatively simple situations. This lack of fundamental understanding is reflected in the absence of proper prediction methods for rupture and fatigue that can be based on a suitable monitoring of the stressed system.

The Role of Heterogeneity.

In the early 1960s, the Japanese seismologist K. Mogi (8, 9) noticed that the fracture process strongly depends on the degree of heterogeneity of materials: the more heterogeneous, the more warnings one gets; the more perfect, the more treacherous is the rupture. The failure of perfect crystals thus seems to be unpredictable whereas the fracture of dirty and deteriorated materials may be forecast. For once, complex systems could be simpler to comprehend! However, since its inception, this idea has not been developed because it is hard to quantify the degrees of “useful” heterogeneity, which probably depend on other factors such as the nature of the stress field, the presence of water, etc. In our work on the failure of mechanical systems, we have solved this paradox quantitatively by using concepts inspired from statistical physics, a domain where complexity has long been studied as resulting from collective behavior. The idea is that, after loading a heterogeneous material, single isolated microcracks appear and then, with the increase of load or time of loading, they both grow and multiply leading to an increase in the number of cracks. As a consequence, microcracks begin to merge until a “critical density” of cracks is reached at which time the main fracture is formed. It is then expected that various physical quantities (acoustic emission, elastic, transport, electric properties, etc.) will vary. However, the nature of this variation depends on the heterogeneity. The new result is that there is a threshold that can be calculated; if disorder is too small, then the precursory signals are essentially absent and prediction is impossible. If heterogeneity is large, rupture is more continuous.

To obtain this insight, we used simple mechanical models of masses and springs with local stress transfer (10). This class of models provides a simplified description to identify the different regimes of behavior. The scientific enterprise is paved with such reductionism that has worked surprisingly well. We were thus able to quantify how heterogeneity plays the role of a relevant field: systems with limited stress amplification exhibit a so-called tricritical transition, from a Griffith-type abrupt rupture (first-order) regime to a progressive damage (critical) regime as the disorder increases. This effect was also demonstrated on a simple mean-field model of rupture, known as the democratic fiber bundle model. It is remarkable that the disorder is so relevant as to change the nature of rupture. In systems with long-range elasticity, the nature of the rupture process may not change qualitatively as above, but quantitatively. Any disorder may be relevant in this case and make the rupture similar to a critical point; however, we have recently shown that the disorder controls the width of the critical region (11). The smaller it is, the smaller will be the critical region, which may become too small to play any role in practice. For realistic systems, long-range correlations transported by the stress field around defects and cracks make the problem more subtle. Time dependence is expected to be a crucial aspect in the process of correlation building in these processes. As the damage increases, a new “phase” appears, where microcracks begin to merge, leading to screening and other cooperative effects. Finally, the main fracture is formed, leading to global failure. In simple intuitive terms, the failure of compositive systems may often be viewed as the result of a correlated percolation process. The challenge is to describe the transition from the damage and corrosion processes at the microscopic level to the macroscopic rupture.

Scaling, Critical Point, and Rupture Prediction.

In 1992, we proposed a model of rupture with a realistic dynamical law for the evolution of damage, modeled as a space-dependent damage variable, a realistic loading, and with many growing interacting microcracks (12–14). We found that the total rate of damage, as measured for instance by the elastic energy released per unit time, increases as a power law of the time to failure on the approach to the global failure. In this model, rupture was indeed found to occur as the culmination of the progressive nucleation, growth, and fusion among microcracks, leading to a fractal network, but the exponents were found to be nonuniversal and a function of the damage law. This model has since been found to describe correctly experiments on the electric breakdown of insulator-conducting composites (15). Another application is damage by electromigration of polycrystalline metal films (16, 17).

In 1993, we extended these results by testing on engineering composite structures the concept that failure in fiber composites may be described by a critical state, thus predicting that the rate of damage would exhibit a power law behavior (18). This critical behavior may correspond to an acceleration of the rate of energy release or to a deceleration, depending on the nature and range of the stress transfer mechanism and on the loading procedure. We based our approach on a theory of many interacting elements called the renormalization group. The renormalization group can be thought of as a construction scheme or “bottom-up” approach to the design of large-scale structures. Since then, other numerical simulations of statistical rupture models and controlled experiments have confirmed that, near the global failure point, the cumulative elastic energy released during fracturing of heterogeneous solids follows a power law behavior.

Based on an extension of the usual solutions of the renormalization group and on explicit numerical and theoretical calculations, we were thus led to propose that the power law behavior of the time to failure analysis should be corrected for the presence of log-periodic modulations (18). Since then, this method has been tested extensively during our continuing collaboration with the French Aerospace company Aérospatiale on pressure tanks made of kevlar-matrix and carbon-matrix composites that are embarked on the European Ariane 4 and 5 rockets. In a nutshell, the method consists in this application in recording acoustic emissions under constant stress rate, and the acoustic emission energy as a function of stress is fitted by the above log-periodic critical theory. One of the parameters is the time of failure, and the fit thus provides a “prediction” when the sample is not brought to failure in the first test. Improvements of the theory and of the fitting formula were applied to about 50 pressure tanks. The results indicate that a precision of a few percent in the determination of the stress at rupture is obtained by using acoustic emission recorded 20% below the stress at rupture. These successes have warranted an international patent, and the selection of this nondestructive evaluation technique as the routine qualifying procedure in the industrial fabrication process. See ref. 19 for a recent synthesis and reanalysis.

This example constitutes a remarkable case where rather abstract theoretical concepts borrowed from the rather esoteric field of statistical and nonlinear physics have been applied directly to a concrete industrial problem. This example is remarkable for another reason that we describe now.

Discrete Scale Invariance, Complex Exponents, and Log-Periodicity.

During our research on the acoustic emissions of the industrial pressure tank of the European Ariane rocket, we discovered the existence of log-periodic scaling in nonhierarchical systems. To fix ideas, consider the acoustic energy E ∼ (t_c − t)^−α following a power law, a function of time to failure. Suppose that there is in addition a log-periodic signal modulation

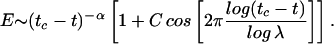We see that the local maxima of the signal occur at t_n such that the argument of the cosine is close to a multiple to 2π, leading to a geometrical time series t_c − t_n ∼ λ⁻ⁿ, where n is an integer. The oscillations are thus modulated in frequency with a geometric increase of the frequency on the approach to the critical point t_c. This apparent esoteric property turns out to be surprisingly general both experimentally and theoretically and we are probably only at the beginning of our understanding of it. From a formal point of view, log-periodicity can be shown to be nothing but the concrete expression of the fact that exponents, or more generally, dimensions, can be “complex,” i.e., belong to these numbers which when squared can give negative values.

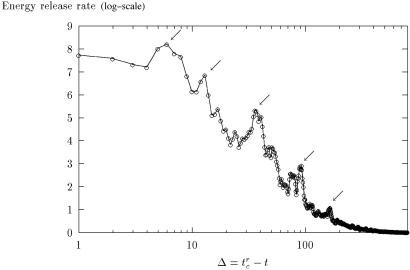
In Fig. 1, we illustrate how log-periodicity helps us to understand the time dependence of signals precursors to global failure in a numerical network of discrete fuses. This so-called time to failure analysis is based on the detection of an acceleration of some measured signal, for instance acoustic emissions, on the approach to the global failure. Similar results are obtained, using Eq. 1 to fit the cumulative energy released by small earthquakes before a major rockburst in a deep South African mine, where the data are of particularly good quality (20).

Fig 1.

Log-log plot of the energy release rate of a mechanical system approaching rupture. A so-called “canonical” averaging procedure (74) has been performed on over 19 independent systems to exhibit the characteristic time scales shown as the arrows decorating the overall power law time to failure behavior.

Encouraged by our observation of log-periodicity in rupture phenomena, we started to investigate whether similar signatures could be observed in other systems. Looking closer, we were led to find them in many systems in which they had been previously unsuspected. These structures have long been known as possible from the formal solutions of renormalization group equations in the 70s but were rejected as physically irrelevant. They were studied in the 80s in a rather academic context of special artificial hierarchical geometrical systems. Our work led us to realize that discrete scale invariance and its associated complex exponents and log-periodicity may appear “spontaneously” in natural systems, i.e., without the need for a preexisting hierarchy. Examples that we have documented (21) are diffusion-limited aggregation clusters, rupture in heterogeneous systems, earthquakes, and animals (a generalization of percolation), among many other systems. Complex scaling could also be relevant to turbulence, to the physics of disordered systems, as well as to the description of out of equilibrium dynamical systems. Some of the physical mechanisms at the origin of these structures are now better understood. General considerations using the framework of field theories, the framework to describe fundamental particle physics and condensed matter systems, show that they should constitute the rule rather than the exception, similarly to the realization that chaotic (nonintegrable) dynamical systems are more general that regular (integrable) ones. In addition to a fascinating physical relevance of this abstract notion of complex dimensions, the even more important aspect in our point of view is that discrete scale invariance and its signatures may provide new insights in the underlying mechanisms of scale invariance and prove very useful for prediction purposes.

Toward a Prediction of Earthquakes?

Nature of the Problem.

An important effort is carried out worldwide in the hope that, maybe sometime in the future, the grail of useful earthquake prediction will be attained. Among others, the research comprises continuous observations of crustal movement and geodetic surveys, seismic observations, geoelectric-geomagnetic observations, and geochemical and groundwater measurements. The seismological community has been criticized in the past for promising results by using various prediction techniques (e.g., anomalous seismic wave propagations, dilatancy diffusion, Mogi donuts, pattern recognition algorithms, etc.) that have not delivered to the expected level. The need for a reassessment of the physical processes has been recognized and more fundamental studies are pursued on crustal structures in seismogenic zones, historical earthquakes, active faults, laboratory fracture experiments, earthquake source processes, etc.

There is even now an opinion that earthquakes could be inherently unpredictable (5). The argument is that past failures and recent theories suggest fundamental obstacles to prediction. It is then proposed that the emphasis be placed on basic research in earthquake science, real-time seismic warning systems, and long-term probabilistic earthquake hazard studies. It is true that useful predictions are not available at present and seem hard to get in the near future, but would it not be a little presumptuous to claim that prediction is impossible? Many past examples in the development of science have taught us that unexpected discoveries can modify completely what was previously considered possible or not. In the context of earthquakes, the problem is made more complex by the societal implications of prediction with, in particular, the question of where to direct in an optimal way the limited available resources.

We here focus on the scientific problem and describe a new direction that suggests reason for optimism. Recall that an earthquake is triggered when a mechanical instability occurs and a fracture (the sudden slip of a fault) appears in a part of the earth's crust. The earth's crust is, in general, complex (in composition, strength, and faulting), and groundwater may play an important role. How can one expect to unravel this complexity and achieve a useful degree of prediction?

Large Earthquakes.

There is a series of surprising and somewhat controversial studies showing that many large earthquakes have been preceded by an increase in the number of intermediate-sized events. The relation between these intermediate-sized events and the subsequent main event has only recently been recognized because the precursory events occur over such a large area that they do not fit prior definitions of foreshocks (22). In particular, the 11 earthquakes in California with magnitudes greater than 6.8 in the last century are associated with an increase of precursory intermediate-magnitude earthquakes measured in a running time window of 5 years (23). What is strange about the result is that the precursory pattern occurred with distances of the order of 300–500 km from the future epicenter, i.e., at distances up to 10 times larger that the size of the future earthquake rupture. Furthermore, the increased intermediate magnitude activity switched off rapidly after a big earthquake in about half of the cases. This finding implies that stress changes caused by an earthquake of rupture dimension as small as 35 km can influence the stress distribution to distances more than 10 times its size. This result defies usual models.

This observation is not isolated. There is mounting evidence that the rate of occurrence of intermediate earthquakes increases in the tens of years preceding a major event. Sykes and Jaume (24) present evidence that the occurrence of events in the range 5.0–5.9 accelerated in the tens of years preceding the large San Francisco Bay area quakes in 1868, 1906, and 1989, and the Desert Hot Springs earthquake in 1948. Lindh (25) points out references to similar increases in intermediate seismicity before the large 1857 earthquake in Southern California and before the 1707 Kwanto and the 1923 Tokyo earthquakes in Japan. Recently, Jones (26) has documented a similar increase in intermediate activity over the past 8 years in Southern California. This increase in activity is limited to events in excess of M = 5.0; no increase in activity is apparent when all events M > 4.0 are considered. Ellsworth et al. (27) also reported that the increase in activity was limited to events larger than M = 5 before the 1989 Loma Prieta earthquake in the San Francisco Bay area. Bufe and Varnes (28) have analyzed the increase in activity that preceded the 1989 Loma Prieta earthquake in the San Francisco Bay area while Bufe et al. (29) document a current increase in seismicity in several segments of the Aleutian arc.

Recently, we have investigated more quantitatively these observations and asked what is the law, if any, controlling the increase of the precursory activity (30). Inspired by our previous considerations of the critical nature of rupture and extending it to seismicity, we have invented a systematic procedure to test for the existence of critical behavior and to identify the region approaching criticality, based on a comparison of the observed cumulative energy (Benioff strain) release and the accelerating seismicity predicted by theory. This method has been used to find the critical region before all earthquakes along the Californian San Andreas system since 1950 with M ≥ 6.5. The statistical significance of our results was assessed by performing the same procedure on a large number of randomly generated synthetic catalogs. The null hypothesis, which is the observed acceleration in all these earthquakes could result from spurious patterns generated by our procedure in purely random catalogs, was rejected with 99.5% confidence (30). An empirical relation between the logarithm of the critical region radius (R) and the magnitude of the final event (M) was found, such that log R ∼ 0.5M, suggesting that the largest probable event in a given region scales with the size of the regional fault network.

Log-Periodicity?

We must add a third and last touch to the picture, which uses the concept of discrete scale invariance, its associated complex exponents, and log-periodicity as discussed above. In the presence of the frozen nature of the disorder together with stress-amplification effects, we showed that the critical behavior of rupture is described by complex exponents. In other words, the measurable physical quantities can exhibit a power law behavior (real part of the exponents) with superimposed log-periodic oscillations (caused by the imaginary part of the exponents). Physically, this stems from a spontaneous organization on a fractal fault system with “discrete scale invariance.” The practical upshot is that the log-periodic undulations may help in “synchronizing” a better fit to the data. In the numerical model (75), most of the large earthquakes whose period is of the order of a century can be predicted in this way 4 years in advance with a precision better than 1 year. For the real earth, we do not know yet, as several difficulties hinder a practical implementation, such as the definition of the relevant space–time domain. A few encouraging results have been obtained but much remains to test these ideas systematically, especially using the methodology presented above to detect the regional domain of critical maturation before a large earthquake (31).

Although encouraging and suggestive, extreme caution should be exercised before even proposing that this method is useful for predictive purpose (see refs. 32 and 33 for potential problems and refs. 20, 34, and 35 for positive evidence). The theory is beautiful in its self-consistency, however, and, even if probably inaccurate in details, it may provide a useful guideline for the future.

Turbulence and Intermittent Climate Change

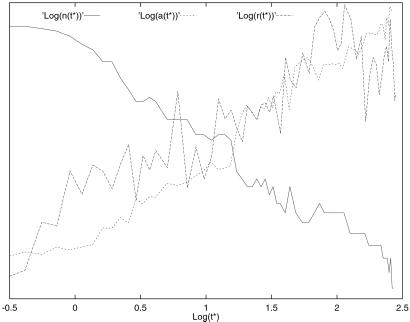
Turbulence is of special interest, both for its applications in astrophysics and geophysics and its theoretical properties. Its main characteristic property is the formation of and interaction among coherent structures or vortices. To illustrate the possible existence and importance of specific features with potential application in geophysical modeling, we identify a signature of turbulent flows in two dimensions (36). In Fig. 2, we analyze freely decaying two-dimensional turbulence experiments (37) and document log-periodic oscillations in the time evolution of the number of vortices n(t*), their radius r(t*), and separation a(t*), which are the hallmarks of a discrete hierarchical structure with a preferred scaling ratio. Physically, this reflects the fact that the time evolution of the vortices is not smooth but punctuated, leading to a preferred scale factor found equal roughly to 1.3. Fig. 2 shows the logarithm ln (a(t*)) of the separation in the range [0.95:1.96], the logarithm ln (r(t*)) of the radius in the range [−0.51:−0.11], and the logarithm ln (n(t*)) of the number of vortices in the range [2.1:4.1], as a function of the logarithm of rescaled time. A straight line corresponds to a power law. We see that the predictions of the usual scaling theory (38) are approximately verified but that significant structures are superimposed on the linear behavior. The spectrum of these structures exhibits a common peak in log-frequency around 4. Synthetic tests show that this common peak at a log-frequency around 4 is significant (36).

Fig 2.

Natural logarithm of the separation, radius, and number of vortices as a function of the natural logarithm of the time in two-dimensional experiments of freely decaying turbulence. The vertical scale is different for each time series (1 to 2 for the logarithm of the separation, −0.5 to 0.1 for the logarithm of the radius, and 2 to 4 for the logarithm of the number of vortices). The approximate linear dependencies in this log–log representation qualify scaling (38). The decorating fluctuations are shown to be genuine structures characterizing an intermittent dynamics (36).

Demonstrating unambiguously the presence of log-periodicity and thus of discrete scale invariance in more general three-dimensional turbulent time series would provide an important step toward a direct demonstration of the Kolmogorov cascade or at least of its hierarchical imprint. For partial indications of log-periodicity in turbulent data, we refer the reader to figure 5.1 (p. 58) and figure 8.6 (p. 128) of ref. 39., figure 3.16 (p. 76) of ref. 40, figure 1b of ref. 41, and figure 2b of ref. 42. See ref. 43 for a proposed mechanism in which scale invariant equations that present an instability at finite wavevector k decreasing with the field amplitude may generate naturally a discrete hierarchy of internal scales. See ref. 76 for a very recent analysis of three-dimensional fully developed turbulence.

Relying on the well known analogies between 2D and quasigeostrophic turbulence (44), this example illustrates the potential of our approach for geophysical flows and climate dynamics (45), as well as for abrupt change of weather regimes. Indeed, considerable attention has been given recently to the likelihood of fairly sudden, and possibly catastrophic, climate change (46). Climate changes on all time scales (47), although no simple scaling behavior has been detected in climate time series. This demands a careful study of records of climate variations with more sophisticated statistical methods. Interactions among multiple space and time scales are typical of a climate system that includes the ocean's (48) and atmosphere's turbulent motions (44).

On the time scale of 10⁴–10⁶ years, it was held for about 2 decades that climate variations are fairly gradual and mostly dictated by secular variations in the earth's orbit around the sun; the latter being quasiperiodic, with a few dominant periodicities between 20,000 and 400,000 years. More recently, however, it has become clear that the so-called mid-Pleistocene transition, at about 900,000 years before the present, involved a fairly sudden jump in the mean global ice volume and sea-surface temperatures, accompanied by a jump in the variance of proxy records of these quantities (49). A subcritical Hopf bifurcation in a coupled ocean–atmosphere–cryosphere model has been proposed as an explanation for the suddenness of this transition (ref. 50 and references therein).

At the other end of the paleoclimate-variability spectrum, sudden changes in the ocean's thermohaline circulation have been associated with the so-called Heinrich (51) events of rapid excursions in the North Atlantic's polar front, about 6000–7000 years apart. These changes could arise from threshold phenomena that accompany highly nonlinear relaxation oscillations in the same coupled model mentioned above (50) or in variations thereof.

On the time scales of direct interest to a single human lifespan, a fairly sharp transition in Northern Hemisphere instrumental temperatures and other fields has been claimed for the mid-1970s (52). This might, in turn, be related to changes in the duration or frequency of occurrence of weather regimes within a single season (53–55). The episodic character of weather patterns and their organization into persistent regimes have been associated with multiple equilibria (56) or multiple attractors (57) in the equations governing large-scale atmospheric flows.

Sudden transitions, i.e., transitions that occur over time intervals that are short compared with what is otherwise the characteristic time scale of the phenomena of interest, are obviously harder to predict than the gradual changes on that time scale. We suggest that the use of methods discussed here could be useful for developing forecasting models for rapid climatic transition.

Predicting Financial Crashes?

Stock market crashes are momentous financial events that are fascinating to academics and practitioners alike. Within the efficient markets literature, only the revelation of a dramatic piece of information can cause a crash, yet in reality even the most thorough postmortem analyses are typically inconclusive as to what this piece of information might have been. For traders, the fear of a crash is a perpetual source of stress, and the onset of the event itself always ruins the lives of some of them, not to mention the impact on the economy.

A few years ago, we advanced the hypothesis (58–64) that stock market crashes are caused by the slow buildup of powerful “subterranean forces” that come together in one critical instant. The use of the word “critical” is not purely literary here. In mathematical terms, complex dynamical systems such as the stock market can go through so-called critical points, defined as the explosion to infinity of a normally well behaved quantity. As a matter of fact, as far as nonlinear dynamic systems go, the existence of critical points may be the rule rather than the exception. Given the puzzling and violent nature of stock market crashes, it is worth investigating whether there could possibly be a link.

In doing so, we have found three major points. First, it is entirely possible to build a dynamic model of the stock market exhibiting well defined critical points that lie within the strict confines of rational expectations, a landmark of economic theory, and is also intuitively appealing. We stress the importance of using the framework of rational expectation in contrast to many other recent attempts. When you invest your money in the stock market, in general you do not do it at random but try somehow to optimize your strategy with your limited amount of information and knowledge. The usual criticism addressed to theories abandoning the rational behavior condition is that the universe of conceivable irrational behavior patterns is much larger than the set of rational patterns. Thus, it is sometimes claimed that allowing for irrationality opens a Pandora's box of ad hoc stories that have little out of sample predictive powers. To deserve consideration, a theory should be parsimonious, explain a range of anomalous patterns in different contexts, and generate new empirical implications.

Second, we find that the mathematical properties of a dynamic system going through a critical point are largely independent of the specific model posited, much more so in fact than “regular” (noncritical) behavior; therefore, our key predictions should be relatively robust to model misspecification.

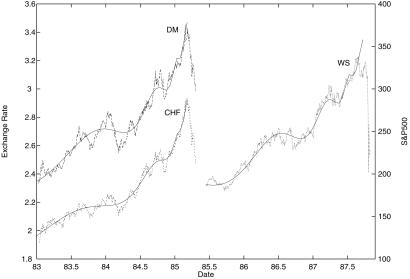
Third, these predictions are strongly borne out in the U.S. stock market crashes of 1929 and 1987. Indeed, it is possible to identify clear signatures of near-critical behavior many years before the crashes (see Fig. 3) and use them to “predict” (out of sample) the date where the system will go critical, which happens to coincide very closely with the realized crash date. We also discovered in a systematic testing procedure, a signature of near-critical behavior that culminated in a 2-week interval in May 1962 where the stock market declined by 12%. That we “discovered” the “slow crash” of 1962 without prior knowledge of it just by trying to fit our theory is a reassuring sign about the integrity of the method. Analyses of more recent data showed a clear maturation toward a critical instability that can be tentatively associated with the turmoil of the U.S. stock market at the end of October 1997. It may come as a surprise that the same theory is applied to epochs so much different in terms of speed of communications and connectivity as 1929 and 1997. It may be that what our theory addresses is the question, “Has human nature changed?”

Fig 3.

The Standard & Poor's 500 U.S. index prior to the October 1987 crash on Wall Street (WS) and the U.S. dollar against Deutschmark (DM) and Swiss Franc (CHF) prior to the collapse in mid-1985. The continuous lines are fits with a power law modified by log-periodic oscillations. See refs. 58–64.

The Crash.

A crash happens when a large group of agents place sell orders simultaneously. This group of agents must create enough of an imbalance in the order book for market makers to be unable to absorb the other side without lowering prices substantially. One curious fact is that the agents in this group typically do not know each other. They did not convene a meeting and decide to provoke a crash. Nor do they take orders from a leader. In fact, most of the time, these agents disagree with one another, and submit roughly as many buy orders as sell orders (these are all of the times when a crash does not happen). The key question is, by what mechanism did they suddenly manage to organize a coordinated sell-off?

We propose the following answer. All of the traders in the world are organized into a network (of family, friends, colleagues, etc.) and they influence each other locally through this network. Specifically, if I am directly connected with k nearest neighbors, then there are only two forces that influence my opinion: (i) the opinions of these k people and (ii) an idiosyncratic signal that I alone receive. Our working assumption here is that agents tend to imitate the opinions of their nearest neighbors, not contradict them. It is easy to see that force (i) will tend to create order, whereas force (ii) will tend to create disorder. The main story that we are telling in here is the fight between order and disorder. As far as asset prices are concerned, a crash happens when order wins (everybody has the same opinion: selling), and normal times are when disorder wins (buyers and sellers disagree with each other and roughly balance each other out). We must stress that this is exactly the opposite of the popular characterization of crashes as times of chaos.

We claim that models of a crash that combine the following features:

1. A system of noise traders who are influenced by their neighbors;

2. Local imitation propagating spontaneously into global cooperation;

3. Global cooperation among noise traders causing a crash;

4. Prices related to the properties of this system;

5. System parameters evolving slowly through time;

would display the same characteristics as ours, namely prices following a power law in the neighborhood of some critical date, with either a real or complex critical exponent. What all models in this class would have in common is that the crash is most likely to occur when the locally imitative system goes through a critical point.

Strictly speaking, these renormalization group equations developed to describe the approach to a critical market crash are approximations valid only in the neighborhood of the critical point. We have proposed a more general formula with additional degrees of freedom to better capture the behavior away from the critical point. The specific way in which these degrees of freedom are introduced is based on a finer analysis of the renormalization group theory that is equivalent to including the next term in a systematic expansion around the critical point and introduce a log-periodic component to the market price behavior.

Extended Efficiency and Systemic Instability.

Our main point is that the market anticipates the crash in a subtle self-organized and cooperative fashion, hence releasing precursory “fingerprints” observable in the stock market prices. In other words, this implies that market prices contain information on impending crashes. Our results suggest a weaker form of the “weak efficient market hypothesis” (65), according to which the market prices contain, in addition to the information generally available to all, subtle informations formed by the global market that most or all individual traders have not yet learned to decipher and use. Instead of the usual interpretation of the efficient market hypothesis in which traders extract and incorporate consciously (by their actions) all informations contained in the market prices, it may be that the market as a whole can exhibit an “emergent” behavior not shared by any of its constituents. In other words, we have in mind the process of the emergence of intelligent behaviors at a macroscopic scale of which the individuals at the microscopic scale have no idea. This process has been discussed in biology, for instance, in animal populations such as ant colonies or in connection with the emergence of consciousness (66, 67). The usual efficient market hypothesis will be recovered in this context when the traders learn how to extract this novel collective information and act on it.

Most previous models proposed for crashes have pondered the possible mechanisms to explain the collapse of the price at very short time scales. Here, in contrast, we propose that the underlying cause of the crash must be searched for years before it in the progressive accelerating ascent of the market price, the speculative bubble, reflecting an increasing build-up of the market cooperativity. From that point of view, the specific manner by which prices collapsed is not of real importance because, according to the concept of the critical point, any small disturbance or process may have triggered the instability, once ripe. The intrinsic divergence of the sensitivity and the growing instability of the market close to a critical point might explain why attempts to unravel the local origin of the crash have been so diverse. Essentially all would work once the system is ripe. Our view is that the crash has an endogeneous origin and that exogeneous shocks only serve as triggering factors. We propose that the origin of the crash is much subtler and is constructed progressively by the market as a whole. In this sense, this phenomenon could be termed a systemic instability. This understanding offers ways to act to mitigate the build-up of conditions favorable to crashes.

A synthesis on the status of this theory as well as all available tests on more than 20 crashes are reported in ref. 68.

Predicting Human Parturition?

Parturition is the act of giving birth. Whereas not usually considered as catastrophic, it is arguably the major event in a life (apart from its termination), and it is interesting that our theoretical approach extends to this situation. This extension is not so surprising in view of the commonalities with the previous examples.

Can we predict parturition? Notwithstanding the large number of investigations on the factors that could trigger parturition in primates, we still do not have a clear signature in any of the measured variables. This situation is in contrast with the situation for other mammals such as cats, cows, etc., for which the secretion of a specific hormone can be linked unambiguously to the triggering of parturition.

Knowledge of precursors and predictors of human parturition would be important both for our understanding of the controlling mechanisms and for practical use for detection and diagnostic of various abnormalities of the birth process. They involve a multitude of genetic, metabolic, nutritional, hormonal, and environmental factors. Present research is hindered, however, by the lack of a clear recognized correlation between the time evolution of these various variables with the initiation of parturition.

Critical Theory of Parturition.

In collaboration with a team of obstetricians, we have proposed (69) a coherent logical framework that allows us to rationalize the various laboratory and clinical observations on the maturation, the triggering mechanisms of parturition, the existence of various abnormal patterns, as well as the effect of external stimulations of various kinds. Within the proposed mathematical model, parturition is seen as a “critical” instability or phase transition from a state of quietness, characterized by a weak incoherent activity of the uterus in its various parts as a function of time (state of activity of many small incoherent intermittent oscillators), to a state of globally coherent contractions where the uterus functions as a single macroscopic oscillator leading to the expulsion of the baby. Our approach gives a number of new predictions and suggests a strategy for future research and clinical studies, which present interesting potentials for improvements in predicting methods and in describing various prenatal abnormal situations.

We have proposed to view the occurrence of parturition as an instability, in which the control parameter is a maturity parameter (MP), roughly proportional to time, and the order parameter is the amplitude of the coherent global uterine activity in the parturition regime. This idea is summarized by the concept of a so-called supercritical bifurcation. This simple view is in apparent contradiction with the extreme complexity of the fetus–mother system, which can be addressed at several levels of descriptions, starting at the highest level from the mother, the fetus, and their coupling through the placenta. For example, in the mother, the myometrium plays an important role in pregnancy, maturation, and onset of labor. It is now well established that the human myometrium is an heterogeneous tissue formed of several layers that differ in their embryological origins and which exhibit quite different histological and pharmaceutical properties. In the uterine corpus, one must distinguish the outer (longitudinal) and the inner (circular) layers. These two layers, composed mainly of smooth muscle cells, are separated by an intermediate layer that is rich in a large amount of vascular and connective tissues but poor in smooth muscle cells. The inner and outer muscle layers have different patterns of contractility and differ in their response and sensitivity to contractile and relaxant agents. This is just an example of the complexity that goes on down to the molecular level, with the action of many substances providing positive and negative feedbacks evolving as a function of maturation. The basis of our simple theory relies on many recent works in a variety of domains (mathematics, hydrodynamics, optics, chemistry, biology, etc.) that have shown that a lot of complex systems consisting of many nonlinear coupled subsystems or components may self-organize and exhibit coherent behavior of a macroscopic scale in time and/or space, in suitable conditions. The Rayleigh–Bénard fluid convection experiment is one of the simplest paradigms for this type of behavior. The coherent behavior appears generically when the coupling between the different components becomes strong enough to trigger or synchronize the initially incoherent subsystems. There are many observations in human parturition where an increasing “coupling” is associated with maturation of the fetus leading to the cooperative synchronized action of all muscle fibers of the uterus characteristic of labor.

Predictions.

Perhaps the most vivid illustration of the increasing coupling as maturation increases is provided by monitoring the uterine activity, using standard external techniques. Away from term, the muscle contractions during gestation are generally weak and characterized by local bursts of activity both in time and space. Increasing uterine activity is observed when the term is approaching, culminating in a complete modification of behavior where regular globally coherent contractions reflects the spatial and time coherence of all of the muscles constituting the uterus. The transition between the premature regime and the parturition regime at maturity is characterized by a systematic tendency to increasing uterine activity, both in amplitude, duration of the bursts, and spatial extension of the activated uterine domains. The susceptibility of the fetus–mother system (to influence the uterine response) to external perturbations or stimulations seems to increase notably on the approach of parturition, because important modifications and reactions of the uterus may result from relatively small stimuli from the mother or fetus.

The main prediction is that, on the approach to the critical instability, one expects a characteristic increase of the fluctuations of uterine activity. Other quantities that could be measured and which are related to the uterine activity are expected to present a similar behavior. The cooperative nature of maturation and parturition proposed here rationalizes the present inability to establish unequivocally predictive parameters of the biochemical events preceding myometrical activity and/or cervical ripening involved in preterm labor. Our theory suggests a precise experimental methodology to obtain an early diagnosis, essential for the efficient treatment of prematurity, which still constitutes the major cause of neonatal morbidity and mortality. In particular, monitoring muscle tremors or vibrations as a function of time of muscle fibers of the uterus would provide quantitative tests of the theory with respect to the spatiotemporal build-up of contractile fluctuations. Our theory also correctly accounts for the observations that external factors affecting the mother such as heavy work and psychological stress are able to modify the maturity of the uterus measured by the progressive modification of the cervix and more frequent uterine contractions. These external factors, in addition to produce direct contraction stimulations, could also be able to modify the postmaturity parameter and control the susceptibility of the fetus–mother system to small influences that can trigger the change from discordant contractions to concordant contractions of a premature or postmature labor.

We note finally that the whole policy for the description of risk factors has been based on an implicit and unformalized hypothesis of a critical transition, which is explicated in our theoretical framework. The prevention program for preterm deliveries (70, 71) was also based on the hypothesis of such a critical transition and the understanding that a small reduction of a triggering factor could be enough to prevent the uterus from beginning its critical phase of activity. The high susceptibility of the fetus–mother system to various factors is also at the origin of the fact that the conventional system of calculation of the risk factors does not explain the real success of the prevention that has been observed (70, 71). Effectively applied in France, our system, which is based on this idea of a critical transition, was able to reduce significantly the rate of preterm births for all French women measured on the Haguenau population of pregnant women from 1971 to 1982, or on randomized samples of all French births.

Summary

We have proposed that catastrophes, as they occur in various disciplines, have similarities both in the failure of standard models and the way that systems evolve toward them. We have presented a nontraditional general methodology for the scientific predictions of catastrophic events, based on the concepts and techniques of statistical and nonlinear physics. This approach provides a third line of attack bridging across the two standard strategies of analytical theory and brute-force numerical simulations. It has been successfully applied to problems as varied as failures of engineering structures, stock market crashes and human parturition, with potential for earthquakes.

The review has emphasized the statistical physics point of view, stressing the cascade across scales and the interactions at multiple scales. Recently, a simple two-dimensional dynamical system has been introduced (72) that reaches a singularity (critical point) in finite time decorated by accelerating oscillations caused by the interplay between nonlinear positive feedback and reversal in the inertia. This dynamical system has been shown to provide a fundamental equation for the dynamics of (i) stock market prices going to a crash in the presence of nonlinear trend-followers and nonlinear value investors, (ii) the world human population with a competition between a population-dependent growth rate and a nonlinear dependence on a finite carrying capacity, and (iii) the failure of a material subject to a time-varying stress with a competition between positive geometrical feedback on the damage variable and nonlinear healing. The rich fractal scaling properties of the dynamics have been traced back to the self-similar spiral structure in phase space unfolding around an unstable spiral point at the origin. We expect exciting new developments in this field by using a combination of statistical physics and dynamical system theory.

Let us finally mention possible extensions of this approach for future research on the prediction of societal breakdowns, terrorism, large-scale epidemics, and of the vulnerability of civilizations (73).