Trust, cooperation, and market formation in the U.S. and Japan

Abstract

Compared with the U.S., Japan is believed to have a collectivist culture that nurtures high trust. Results from laboratory and survey research, however, show that Americans are more likely to trust strangers than are Japanese. Why would trust be lower in a collectivist culture? We use an agent-based computational model to explore the evolutionary origin of this puzzling empirical finding. Computer simulations suggest that higher social mobility in the U.S. may be the explanation. With low mobility, agents rarely encounter strangers and thus remain highly parochial, trusting only their neighbors and avoiding open-market transactions with outsiders. With moderate mobility, agents learn to read telltale signs of character so that they can take advantage of better opportunities outside the neighborhood. However, if mobility is too great, there is too little trustworthiness to make the effort to discriminate worthwhile. This finding suggests that higher mobility in the U.S. may explain why Americans are more trusting than Japanese, but if mobility becomes too high, the self-reinforcing high-trust equilibrium could collapse.

Learning Theory and Social Dilemmas

Compared with the U.S., Japan has stronger group obligations, lower deviance, stronger relational commitment, and lower social mobility (1–3). Hagen and Choe (4) report the “widely held view that Japan is a collectivist culture in the sense that people's self-identification tends to be deeply rooted in group membership” (5, 6). This self-identification is thought to promote a greater tendency to trust and cooperate, compared with the “individualist” culture of the U.S.

However, results from laboratory and survey research challenge the conventional wisdom. Yamagishi (7) found that “Japanese subjects, who live in a society which is characterized by strong mutual monitoring and sanctioning, have weaker trust and cooperate less in the absence of a sanctioning system than do American subjects, who live in a more individualistic society.” The same pattern can be observed outside the laboratory, where many Japanese businesses shun better deals in the open market in favor of established suppliers (8). These parochial tendencies toward protection and in-group favoritism run counter to universalistic principles of free trade and cultural pluralism and impose opportunity costs. However, they minimize transaction costs associated with the risk of being cheated by strangers (9). The problem is that most market transactions take place outside embedded relationships and may involve strangers. Parochial avoidance of the outside world traps “low trustors” in a vicious cycle of distrust and xenophobia that leads to a self-reinforcing Pareto-deficient outcome.

Lower trust in a collectivist society poses an interesting puzzle. Why would trust be lower in a society that encourages conformity to prosocial norms? Yamagishi's theory of trust suggests a social-psychological explanation. Japanese tend to believe that trustworthy behavior occurs only when it is prudent, as when transactions are embedded¶ in tight social networks where malfeasance is discouraged by the need to maintain a good reputation in a set of dense social interactions. In contrast, Americans are more likely to believe in character that produces trustworthy behavior even when someone could cheat with impunity. Trustworthy individuals learn to send and receive reliable signals that allow them to avoid miscreants. Thus, Americans focus not on social or physical proximity but on a Calvinist concern for telltale signs of character. Strangers can be trusted if they display appropriate emotional, cultural, and social cues that cannot be easily faked.∥ This strategy allows them to participate in unembedded exchanges in the open market in relative safety.

Yamagishi draws too sharp a line between parochialism and trust, however. We hypothesize that embedded relations are not just a provincial alternative to participation in the open market but are the classroom where the skills are developed for navigating outside the neighborhood, as argued by Stolle (13): “The important question is how the trust that we obviously build for people we know well can be extended and used for the development of generalized trust, or trust for people we do not know well.” And Knight (14) also notes the need to “provide an account of how these (cooperative) expectations extend beyond the instances of interactions with those whom we actually know to a more general expectation of cooperation about the members of a society.”

The need for this account is the point of departure for our theoretical research that uses agent-based computational experiments. We hypothesize that a key variable may be social and spatial mobility that requires local actors to learn how to interact effectively with newcomers. These skills in turn encourage trustworthy strangers to learn to send and receive signals effectively. We hypothesize that signaling systems take root in neighborhoods characterized by relatively dense interactions and then diffuse to other regions through movement of neighbors to socially distant regions. Reliance on signaling, rather than parochial relations, allows the system to move to a Pareto superior equilibrium in which open market transactions are honest and typical.

We use agent-based modeling to see whether we can “grow” an artificial society in which agents must evolve strategies for coping with opportunity costs (the possibility of a better deal outside the local network) as well as transaction costs (notably, the chance of being cheated by one's partner). Agents participate in two types of relationships: with neighbors and with strangers. Interactions with neighbors exhibit a high degree of embeddedness, that is, the relationships are stabile and transitive. In contrast, interactions with strangers are fleeting and random.

Hypotheses

We want to know whether agents can learn to trust and cooperate with strangers and whether the outcome depends on the rate of mobility and the structure of interaction. Mobility can encourage trust in strangers by introducing newcomers to a neighborhood. Newcomers are bound by the same relational constraints on behavior that promote cooperation among neighbors. However, distrust of strangers prevents parochial neighbors from taking advantage of the opportunity. Newcomers thus create a “niche” for the evolution of trust by creating an advantage for those who are willing to selectively trust outsiders who move in.

This theory implies that the effect of mobility on trust is nonlinear. If the mobility rate is too low, neighbors do not have an opportunity to interact with newcomers and to learn that signaling is more efficient than reliance on embedded relationships. Without an effective signaling system, agents will tend to prefer the safety of local interaction. Thus, when social mobility is very low, we expect to grow a society with high network embeddedness, parochial distrust of outsiders, and in-group favoritism. Agents pay the opportunity cost to avoid interaction with outsiders. In this condition, a global market cannot emerge.

When social mobility is moderate, we expect to find a society where people leave their networks to find better deals in the open market. In this condition, transactions move out of the neighborhoods and into a thriving global market.

When social mobility is higher still, we expect a society where life is “nasty brutish and short,” where no one trusts anyone, not even their neighbors, and for good reason. If the mobility rate is too high, almost all of the neighbors become newcomers, which undermines the relational constraints that promote trustworthy behavior.

Thus, the emergence of a global market is expected within a “mobility window” in which movement is neither too low to disturb a parochial equilibrium nor too high to disturb a signaling equilibrium. Inside a window of moderate mobility, enough newcomers move to a neighborhood to make reliance on social cues more effective than indiscriminant parochialism, but there are not so many newcomers that relational constraints are undermined. Once an effective signaling system develops, agents can then use this to discriminate among strangers in market transactions outside the neighborhood. We summarize the hypothesized effects of mobility as follows:

Hypothesis 1: Mobility has an inverted U-shaped effect on trust and participation in market transactions.

We also explored a second structural variable–neighborhood size–that should also affect the tradeoff between transaction and opportunity costs and thus the emergence of unembedded market transactions. Neighborhood size should increase the transaction costs but reduce the opportunity costs of local interaction. On the positive side, the larger the neighborhood, the higher the transaction costs in local interaction. With very small neighborhoods, there is very high network transitivity, which creates evolutionary pressure toward local trustworthiness and reliance on embedded relations as the basis for trust. Local trustworthiness reduces the transaction costs imposed by cheating and malfeasance. In contrast, large neighborhoods increase the coordination complexity of self-organized cooperation. At the extreme, in a population with a single large neighborhood, there is no way to avoid strangers by relying on local interaction. Thus, the smaller the neighborhood, the greater the difference in the “safety” of transactions with neighbors compared with strangers. This effect via transaction costs implies that neighborhood size should have a positive effect on trust in strangers and market formation, by reducing the comparative advantage of parochial strategies.

On the negative side, the larger the neighborhood, the lower the opportunity costs of local interaction. The more partners one can choose among, the higher the probability of finding the partner that is an optimal match. At the extreme, a neighborhood with only two members precludes any opportunity to search for a partner that conforms to individual preferences. Conversely, the opportunity to search is greatest in a population with only one neighborhood. Thus, assuming heterogeneity across partners in the value of exchanges, the smaller the neighborhood, the greater the difference in the value of transactions with neighbors compared with strangers. This effect via opportunity costs implies that neighborhood size should have a negative effect on trust in strangers and market formation, by increasing the comparative advantage of parochial strategies.

Putting the two effects together, we hypothesize a tradeoff between the effect of neighborhood size on increasing transaction costs and reducing opportunity costs of local interaction. There are two possibilities. The opposite effects may “cancel out” such that neighborhood size has no effect on the emergence of the market. Alternatively, like mobility, the effect of neighborhood size may be nonlinear. We summarize these possibilities as the following two hypotheses about the effects of neighborhood size on the emergence of a global market:

Hypothesis 2a: Neighborhood size has no effect on trust and market formation.

Hypothesis 2b: Neighborhood size has a nonlinear effect on trust and market formation.

Experimental Design

We model trust decisions by using a type of Prisoner's Dilemma with an option to exit. Orbell and Dawes (15) point out that real-life Prisoner's Dilemma is rarely played by prisoners. Most exchange partners are free to walk away. The decision to exit may be informed by an estimate of a prospective partner's trustworthiness. Note that trust is conceptually different from cooperation (16). Trust is a decision whether to play the Prisoner's Dilemma game or to exit, not whether to cooperate or defect once the decision has been made to play.

All experiments assume a population of 1,000 agents randomly allocated to positions in a social network. To test the emergence of a global market in a highly parochial population, we clustered agent locations into neighborhoods of randomly varying size. Contact between neighborhoods occurs when agents move from one neighborhood to another or when agents meet in a global market to which all agents have access.

At each iteration, agents involuntarily change neighborhoods with a probability that is manipulated as an experimental treatment.** When an agent moves, it is classified as a newcomer in its new neighborhood for one iteration.†† Although agents do not choose to move, they can choose to interact outside their neighborhood by entering the open market.

Agents who choose to remain in the neighborhood are then randomly paired with one of their neighbors for one exchange. Those who choose to enter the market are randomly paired with another agent in the market. Occasionally, an agent will be unable to find a partner, for one of three reasons: he is the only agent in the market, he is the only agent in the neighborhood, or all potential partners are already paired. When this occurs, the isolate must “sit out” (or “sleep through”) one iteration, with no opportunity to exchange or to learn from experience.

After finding an exchange partner, the agent must decide whether to exchange honestly (“cooperate”) or cheat (“defect”), based on the agent's current probability of cooperation. The combination of propensities for cooperation and entering the market gives each agent the ability to develop a conditional strategy for cooperation, depending on whether the relationship is likely to be ongoing (in the neighborhood) or one shot (in the market).‡‡ Agents then evaluate the trustworthiness of the partner. Parochial agents distrust strangers and trust neighbors. At the other extreme, agents reject parochialism and judge each individual—neighbor or stranger—based on telltale signs of character. Trustworthy agents have an interest in signaling in a way that is difficult for cheaters to mimic, but we assume that these are imperfect. The reliability of the signal depends on the agent's level of trustworthiness. The stronger the agent's commitment to honest (or dishonest) behavior, the less likely their signal will be misleading. Signals from ambivalent agents are highly unreliable (no better than a coin toss).

We assume that trust is symmetrical, that is, each agent is both trustor and trustee, the condition that often arises in social exchange. This is a more difficult problem than asymmetric (or one-way) trust because both sides must be trustworthy and trusting for either side to realize the potential benefits of social exchange. If either side distrusts, the exchange is not consummated and both players receive the exit payoff X. We tested two assumptions about the cost of exit. If agents are highly self-reliant, there is no cost of exit, which we implemented as X = 0. If agents depend on exchange, exit is as costly as an exchange in which both sides cheat, or X = P. If both sides trust, they then play a one-shot Prisoner's Dilemma game with payoffs for mutual cooperation (R) and defection (P) and unilateral cooperation (S) and defection (T). A Prisoner's Dilemma game is defined by the payoff inequality T > R > P > S.

The transaction cost of exchange depends on the level of trustworthiness, which is endogenous to the model. Transaction costs will be higher in the market if noncooperators prefer the anonymity of the market to the embeddedness of local exchange. A higher transaction cost may be offset, however, by the greater opportunity costs of remaining in the relative safety of a small neighborhood. The smaller the pool from which partners are chosen, the lower the probability of finding an exchange partner offering an item that matches an agent's preferences, and hence the lower the expected value of the exchange. Simply put, agents may have a better chance of finding a local exchange partner who is honest but a smaller chance of finding a local partner who has what they want.

We assume that the expected value of the exchange has no effect on the agent's payoff if the partner cheats or distrusts the agent or if the agent distrusts the partner. The expected value only affects the agent's payoff if the partner cooperates. Hence, the S (−0.5) and P (−0.2) payoffs are fixed, but the R and T payoffs depend on the values that are received in the social exchange, which in turn depends on finding a partner whose resources optimize over the agent's preferences. We assume R = 0.7 − 0.5O and T = 1 − 0.5O, where O is the opportunity cost of selecting a partner, given the size of the pool from which an optimal partner is located.

We tested two assumptions about opportunity cost. Homogeneity in the value of exchange partners means there is no opportunity cost in selecting from a small pool. Heterogeneity in the value of exchange partners means that the expected value of the exchange increases with the size of the pool from which partners are chosen. More precisely,

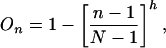where O_n is the opportunity cost of choosing a partner from a pool of size n drawn from a population of size N, and h corresponds to the heterogeneity of the population. If the pool contains the entire population (n = N), or if the population is homogenous (h = 0), then O = 0, which eliminates the opportunity cost of local partner selection. If the population is normally distributed (h = 1) and the pool contains only one agent, then O = 1, which is the maximum opportunity cost. Specifying opportunity costs as a function of the partner-selection pool avoids the need to have agents pair off with their most-preferred partner. Instead, we can use a much simpler pairing algorithm in which partners are chosen randomly, and the effects of optimal pairing are captured instead by O as a function of the size of the selection pool.

The payoffs operate as reinforcements that modify the probability of repeating the associated choices. Initially, these probabilities are randomly assigned from a uniform distribution, with an expectation of 0.5. We then observed whether a global market, characterized by trust and trustworthiness, could emerge from a random start as these probabilities to trust, cooperate, and enter the market are updated through social learning (17). Social learning is based on adaptation to direct and vicarious experience. Social learning can be more efficient than reliance on direct experience because learning is then distributed over a population who search in parallel for a solution. Agents identify as a role model the neighbor with the highest cumulative payoff. (We also experimented with role models selected from the entire population as well as the previous partners.) Social influence then diffuses through networks of interpersonal contact as agents move to new neighborhoods and remain there long enough to no longer be regarded as a newcomer.

Agents also learn from their own experience. We implemented reinforcement learning by using the Bush–Mosteller stochastic learning algorithm (18, 19). The algorithm updates the probability P of repeating action a at time t + 1 as a function of the associated positive or negative payoff π_a (−1 < π < 1) at time t:

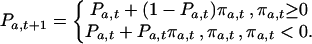Action a is a vector of three stochastic decisions: trust (play or exit), trustworthiness (cooperate or defect), and location (neighborhood or market). Agents build on partial solutions by randomly recombining the “lessons” of direct and vicarious experience across these three decisions. For each decision, there is a 0.5 probability of replacing an individual behavioral propensity with that of the role model.

After agents update their vector of behavioral probabilities, they begin a new iteration, following the same sequence: change location (with some probability), choose to enter the global market or remain in the local neighborhood, randomly choose a partner from the available pool (either the market or the neighborhood), decide whether to cooperate, give the appropriate signal, decide whether to trust the partner (based either on the partner's location or signal), and update stochastic behavioral propensities based on the outcome.

To avoid possible startup anomalies, we allowed agents to play for 1,000 iterations before recording results for an additional 1,000 iterations. This was more than sufficient time for the population to move to either a parochial equilibrium in which agents avoid strangers or to a nonparochial equilibrium in which agents look for better opportunities in the open market while avoiding those who appear suspicious.

We hypothesize that the emergence of the market will depend on two structural conditions: the rate of spatial mobility and the number and size of neighborhoods. We varied the mobility rate from 0 (no one moves) to 1 (everyone moves) in 11 steps of 0.1. We varied the size of neighborhoods from 10 to 100 (in a population of 1,000), in 10 steps of size 10.

Manipulation of mobility and neighborhood size in a full-factorial design created 11 × 10 = 110 treatment conditions. We simulated each condition 20 times, giving 2,200 observations, with 200 observations at each level of mobility and 220 observations at each level of neighborhood size.

Results

We tested hypotheses 1, 2a, and 2b by manipulating the rate of mobility and the size of neighborhoods and observing the effects on the willingness to leave the safety of the neighborhood to exploit the greater opportunities of the open market. We measured trust at three levels: the underlying rule (the average propensity to base trust on the partner's social cues rather than social proximity), the manifest behavior (the rate at which agents actually trust and cooperate in the market and neighborhoods), and the effects on market size (the rate that agents leave the neighborhood and enter the open market).

We tested the effects of mobility and neighborhood size under different assumptions about the incentives to trust strangers. In a population where everyone has similar resources, there is little incentive to look for a better trading opportunity outside the relative safety of embedded relationships. The cost of exit also affects the incentives for learning who can be trusted. There is little incentive to discriminate in a highly self-reliant population where distrust costs nothing (X = 0) or where the cost of exit is so high that one might as well trust everyone (X < P). Not surprisingly, we found that agents are less likely to learn to trust strangers if there is little or no cost for “going it alone” (with X = 0) or settling for local partners (with h = 0), as elaborated below in the sensitivity analysis. We therefore focus our report on the effects of mobility and neighborhood size in a population that is penalized for avoiding exchange (X = P) and avoiding the outside world (h = 1).

Effects of Mobility.

We tested the hypothesized curvilinear effect of mobility by increasing the rate of mobility from M = 0 (no one ever changes neighborhood) to M = 1 (everyone always moves) in steps of 0.1. At each level of mobility, we allowed neighborhood size to vary from n = 10 to n = 100 in steps of 10. We found no significant interaction between mobility and neighborhood size and therefore report only the main effects of mobility. The vertical axes of Figs. 1 and 2 correspond to the expected values of three indicators of market formation (trust in strangers, market size, and reliance on signaling) and two measures of local interaction (trust in newcomers and neighbors). Expected values are the means for 200 observations at each level of mobility (20 replications at each of 10 neighborhood sizes). Results are based on a population (n = 1,000) that values exchange (X = P) and has dissimilar resources, such that there is an opportunity cost for remaining in a small neighborhood with few choices of partners (h = 1).§§

Fig. 1.

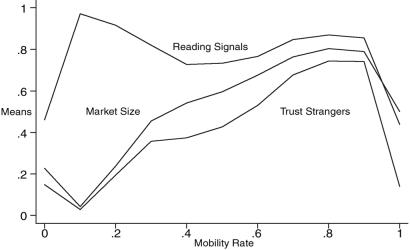
Expected value of three indicators of market interaction, based on 200 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h = 1.

Fig. 2.

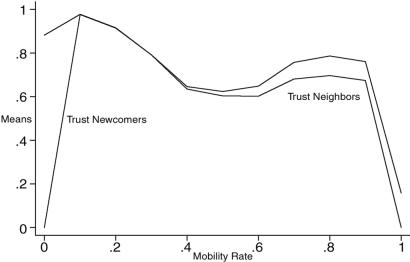
Expected value of two indicators of local interaction, based on 200 observations at each level of mobility, with N = 1,000, n = {10..100}, X = P, h = 1.

Figs. 1 and 2 clearly support the curvilinear effect of mobility predicted in hypothesis 1. With zero mobility, about 85% of neighborhoods lock in high trust in their neighbors but distrust strangers (see Fig. 2; the zero trust in newcomers at zero mobility is simply an artifact of their nonexistence). The remaining 15% of neighborhoods use signaling to lock in high market participation, which removes local exchange as an option (because there is no one left in the neighborhood with whom to interact).

Even small amounts of mobility are sufficient to disrupt the nonparochial equilibrium in these localities, as newcomers move in with different ideas. This causes trust in strangers to drop to near zero at M = 0.1, even though the underlying rule to base trust on social cues increases most rapidly, rising from near 0.5 in the absence of mobility to nearly 1.0 as soon as there is even minimal movement across neighborhoods. This in turn leads to high trust in newcomers (Fig. 2), but not in strangers (Fig. 1). Very small doses of mobility are sufficient to create an incentive for learning to read signals to decide whether to trust newcomers, but this actually lowers the level of trust in strangers, compared with zero mobility.

However, as mobility continues to increase and the proportion of newcomers in the population grows, local trust steadily declines, whereas trust in strangers increases. At very high mobility rates, both local and global trust collapse, because of the adverse effects of mobility on the formation of ongoing local relationships in which cooperation can be a viable strategy.

We also estimated curvilinear regression models¶¶ for all five indicators of market and neighborhood interaction, as linear, quadratic, and cubic functions of the mobility rate. Hypothesis 1 implies that quadratic or cubic functions fit the data better than linear models. Comparison of nested models shows that this is indeed the case. Table 1 reports coefficients for the linear, quadratic, and cubic terms in the expanded model, and the highly significant effects support the predicted curvilinearity for all five measures of the effects of mobility. The rate of reading signals fits best to a quadratic function with a negative coefficient for the quadratic term. The other four measures each fit best to a cubic function, and trajectories of the predicted values show the hypothesized inverted U-shaped patterns. Explained variance averages 29% (ranging from 11% to 42%) over the five indicators, suggesting a very good fit with the curvilinear models.

Table 1.

Curvilinear model of the effect of mobility on five indicators of local and market interaction

	Market size	Read signals	Trust in
			Strangers	Neighbors	Newcomers
Linear	−0.25	0.88	−1.19	−1.95	−5.48
Quad.	4.049	−0.91	6.38	4.40	11.18
Cubic	−3.43	−0.02	−5.08	−3.28	−6.94
Cons.	0.162	0.65	0.156	1.01	1.51
Adj. R2	0.421	0.112	0.276	0.349	0.279
N	2,200	2,200	2,200	2,200	2,000

^*, P < 0.05;

^**, P < 0.01.

^† Cases deleted for M = 0.

These expected equilibrium values over multiple replications obscure the dynamics within each of the 200 observations at each level of mobility. Fig. 3 shows the distribution of the equilibrium outcomes for trust in strangers, broken down by mobility. At zero mobility (foreground of the graph), we observe trust in strangers in about 15% of the population in almost all of the 200 replications. As mobility increases to 0.1, the level of trust in strangers drops to near zero percent. With midrange levels of mobility, trust in strangers shows a bimodal distribution, with zero trust about half the time and universal trust in the other half. As mobility increases further, the bimodal distribution persists, but universal trust becomes progressively more likely as the outcome. However, at total mobility (in which everyone is always a newcomer), the distribution is again unimodal, with low (but nonzero) levels of trust over 90% of the time.

Fig. 3.

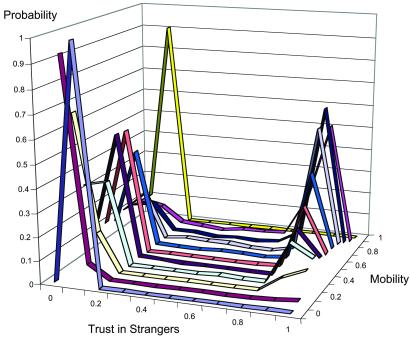
Distribution of trust in strangers by mobility rate with N = 1,000, n = {10..100}, X = P, h = 1.

Effects of Neighborhood Size.

We tested the hypothesized countervailing effects of neighborhood size by increasing the number of neighborhoods from 10 to 100 and then randomly dispersing the population of 1,000 agents across locations. Thus, not all neighborhoods are the same size, and the size changes as agents move around. At each mean neighborhood size, we allowed the rate of mobility to vary from 0 to 1 in steps of 0.1. We found no significant interaction between mobility and neighborhood size and therefore report only the main effects of neighborhood size on three measures of market interaction (Fig. 4) and two measures of local interaction (Fig. 5). Figs. 4 and 5 show that all five measures increase quickly as neighborhood size increases from 10 to 20. For n > 20, however, there is little or no effect of neighborhood size. The results support hypothesis 2b (nonlinear effect) more than hypothesis 2a (no effect). They also suggest that the positive effect of neighborhood size (by the increase in local transaction costs) may outweigh the negative effect (by the decrease in local opportunity costs), but even this effect disappears quickly as neighborhood size continues to increase.

Fig. 4.

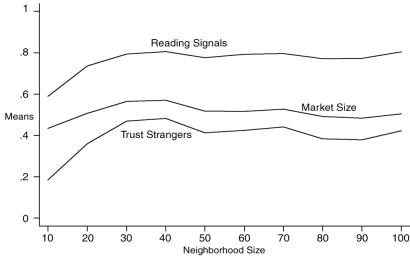
Expected value of three indicators of market interaction, based on 220 observations at each neighborhood size, with N = 1,000, M ={0..1}, X = P, h = 1.

Fig. 5.

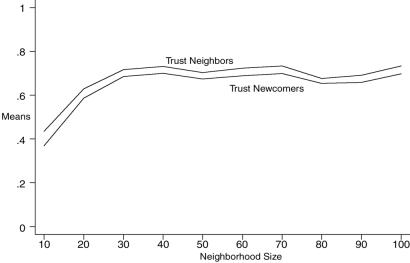
Expected value of two indicators of local interaction, based on 220 observations at each neighborhood size, with N = 1,000, M ={0..1}, X = P, h = 1.

We also estimated curvilinear regression models for all five indicators of market and neighborhood interaction, as linear, quadratic, and cubic functions of neighborhood size. Hypothesis 2a implies an equally poor fit for all three functional forms, whereas hypothesis 2b implies that quadratic or cubic functions fit the data better than linear models. The highly significant coefficients for the quadratic and cubic terms in Table 2 confirm hypothesis 2b, but the adjusted R²s are very low for all five measures (averaging only about 4% explained variance). This finding suggests that the effect of neighborhood size is very weak, compared with the effects of mobility.

Table 2.

Curvilinear model of the effect of neighborhood size (rescaled 0.1 to 1) on five indicators of local and market interaction

	Market size	Read signals	Trust in
			Strangers	Neighbors	Newcomers
Linear	1.421	2.038	2.921	2.837	3.110
Quad.	−2.630	−3.482	−5.129	−4.798	−5.206
Cubic	1.395	1.820	2.682	2.485	2.673
Cons.	0.321	0.433	−0.047	0.213	0.127
Adj. R2	0.008	0.054	0.031	0.056	0.084
N	2,200	2,200	2,200	2,200	2,200

^*, P < 0.05;

^**, P < 0.01.

As an additional test, we measured the effects of neighborhood size in a world where all partners have equally valued resources, such that there is no opportunity cost for remaining in the relative safety of embedded relationships, even in small neighborhoods. If hypothesis 2a is correct, having removed the countervailing negative effect of neighborhood size (by opportunity costs), we should now find a stronger positive effect with h = 0 (caused by the effect via transaction costs). Instead, we observe an even weaker effect of neighborhood size than with h = 1. This is confirmed by curvilinear regression analysis, which shows neither a linear, quadratic, or cubic effect of neighborhood size in a society with h = 0. With no opportunity cost for local interaction, the population fails to learn to trust strangers, regardless of neighborhood size. In short, the analysis of neighborhood size suggests that trust in strangers is not possible when neighborhoods are extremely small or when there is no opportunity cost for local interaction, but otherwise, the size of neighborhoods has relatively little effect. A tentative conclusion is that differences in trust between the U.S. and Japan may be caused by differences in social mobility, but do not appear to reflect differences in the structure of social networks in the two societies.

Sensitivity Analysis

We further tested the robustness of the results by testing the effects of mobility with h = 0, such that the expected value of exchange did not vary across partners. This process eliminated any incentive to search for better deals outside the relative safety of embedded relationships, even if the neighborhood is very small. Not surprisingly, eliminating the opportunity cost of parochial strategies had no effect on local interactions. The effect of mobility on trust in neighbors and newcomers is virtually identical to what was observed with h = 1 (see Fig. 2). However, the effect of mobility on trust in strangers and attraction to the market is much weaker with h = 0, and the trajectory is linear rather than the inverted U observed in Fig. 1. In short, the absence of opportunity costs for local interaction removed an important incentive for agents to learn to trust strangers, regardless of mobility rates. Agents still learned to read social cues about who can be trusted (especially at moderate levels of mobility), but these were used mainly for trusting newcomers in the neighborhood rather than strangers in the market. When there is no opportunity cost for remaining in the local neighborhood, agents are less eager to enter potentially risky exchanges with strangers.

We also tested robustness over alternate assumptions about the initial behavioral probabilities and the cost of exit. Instead of a random start, we initialized the population as an extremely parochial world (high probabilities to cooperate, trust only neighbors, and avoid the market) and as a “Hobbesian” world (high probability to enter the market to “hit and run”). The nonlinear effects of mobility on trust in strangers and attraction to the market were less pronounced when we assumed an initially parochial population (compared with a random start), but the inverted U remains clearly evident. In contrast, the curvilinear effect on reading signals was even more dramatic than with a random start.

The dynamics with a Hobbesian start were also very similar to those with a random start. The effects of mobility on signaling and trust in strangers, newcomers, and neighbors were very similar to what we observe in Figs. 1 and 2, although the overall level of trust in strangers was somewhat lower. The effect of mobility on market size was also very similar to Fig. 1, except when the mobility rate reached 100%. In the absence of ongoing local relationships, agents never learn to cooperate, and having started out in the market, agents never learn to go back into neighborhoods that are just as treacherous.

We also tested the effects of self-reliance by assuming a world in which exit was not costly (X = 0). Not surprisingly, it was somewhat more difficult for self-reliant populations to learn to trust when distrust was an easy option, but the inverted-U effect of mobility remained strikingly evident for all indicators except market size.

Discussion and Conclusion

This theoretical research was motivated by the need to explain an empirical anomaly in studies of cross-national differences in trust: Why do highly individualistic Americans show higher trust than do the collectivist Japanese? We hypothesized that the explanation centers on cross-national differences in social and spatial mobility. Although the Japanese lifetime employment system is limited to the larger firms (20), the inter-firm mobility rate is nevertheless much lower in Japan than in the U.S. Following Yamagishi (7, 9), we hypothesize that lower inter-firm mobility encourages reliance on parochial loyalty and prevents development of the social skills required for effective signaling. Americans, on the other hand, develop these skills as they negotiate interactions with newcomers in the relative safety of embedded relationships. With these social skills, Americans can then navigate through a global market that is risky but full of opportunities for those who know how to avoid unsavory characters.

Clearly, the coincidence of cross-national differences in mobility and trust is not sufficient to establish a causal relationship. Nor does it help us identify the causal mechanism at the level of microinteraction. To that end, we used an agent-based computational model to test the internal logical validity of the theory. The results support the hypothesized curvilinear effects of mobility. Even very low mobility rates are sufficient to motivate reliance on signaling, but this is used only to decide whether to trust newcomers, while continuing to avoid strangers outside the relative safety of embedded relationships. However, as mobility increases further, so, too, does the probability of a nonparochial equilibrium, but only up to a point. Very high mobility undermines the embedded relationships in which trust in strangers can take root. Compared with the effects of mobility, neighborhood size has relatively little impact. These results suggest that differences in parochialism between the U.S. and Japan may reflect the higher rates of mobility in the U.S. but not differences in the structures of local interaction.

Sensitivity analysis showed that these effects are most evident under conditions that encourage agents to acquire the social skills for negotiating an uncertain world—high costs of going it alone (e.g., X = P) and remaining near home (e.g., h = 1). The results are robust over alternative assumptions about start values and the cost of exit, although the overall levels of trust in strangers and preference for market interaction are somewhat lower.

This study makes several simplifying assumptions that might usefully be relaxed in follow-up studies that elaborate and extend this design:

•Allow local reputations to be formed and diffused through the neighborhood.

•Allow agents to decide whether to trust the accuracy of reputational information (a.k.a. “gossip”).

•Allow agents to learn how to fake signals of trustworthiness and to spot the fakers.

•Allow agents to decide whether to move, such that the mobility rate becomes endogenous to the model.

•Relax the assumption of random mobility by implementing mobility chains, in which agents' destinations are biased by the paths followed by previous movers.

•Allow agents to form ongoing relationships in the market, such that reliance on reading signals becomes less important.

•Give agents more sophisticated cognitive abilities, such as conditional strategies.

Although it is always tempting to explore new theoretical possibilities, a more complex model also makes it more difficult to understand the causal mechanism underlying the observed patterns. The results from this study, based on a relatively simple design, are not only useful for identifying possible causal mechanisms for observed cross-societal differences, they are also useful for identifying empirical possibilities that have not yet been observed but which might nevertheless be obtained if current trends were to continue. In particular, the nonmonotonic effects of mobility raise a warning flag for the U.S. Although American society enjoys relatively high trust and participation in global markets, there is no guarantee that this will continue indefinitely. Rapid advances in telecommunications could undermine the embeddedness of social relationships needed to make trust and trustworthiness self-reinforcing.