Agent-based modeling: Methods and techniques for simulating human systems

Abstract

Agent-based modeling is a powerful simulation modeling technique that has seen a number of applications in the last few years, including applications to real-world business problems. After the basic principles of agent-based simulation are briefly introduced, its four areas of application are discussed by using real-world applications: flow simulation, organizational simulation, market simulation, and diffusion simulation. For each category, one or several business applications are described and analyzed.

In agent-based modeling (ABM), a system is modeled as a collection of autonomous decision-making entities called agents. Each agent individually assesses its situation and makes decisions on the basis of a set of rules. Agents may execute various behaviors appropriate for the system they represent—for example, producing, consuming, or selling. Repetitive competitive interactions between agents are a feature of agent-based modeling, which relies on the power of computers to explore dynamics out of the reach of pure mathematical methods (1, 2). At the simplest level, an agent-based model consists of a system of agents and the relationships between them. Even a simple agent-based model can exhibit complex behavior patterns (3) and provide valuable information about the dynamics of the real-world system that it emulates. In addition, agents may be capable of evolving, allowing unanticipated behaviors to emerge. Sophisticated ABM sometimes incorporates neural networks, evolutionary algorithms, or other learning techniques to allow realistic learning and adaptation.

ABM is a mindset more than a technology. The ABM mindset consists of describing a system from the perspective of its constituent units. A number of researchers think that the alternative to ABM is traditional differential equation modeling; this is wrong, as a set of differential equations, each describing the dynamics of one of the system's constituent units, is an agent-based model. A synonym of ABM would be microscopic modeling, and an alternative would be macroscopic modeling. As the ABM mindset is starting to enjoy significant popularity, it is a good time to redefine why it is useful and when ABM should be used. These are the questions this paper addresses, first by reviewing and classifying the benefits of ABM and then by providing a variety of examples in which the benefits will be clearly described. What the reader will be able to take home is a clear view of when and how to use ABM. One of the reasons underlying ABM's popularity is its ease of implementation: indeed, once one has heard about ABM, it is easy to program an agent-based model. Because the technique is easy to use, one may wrongly think the concepts are easy to master. But although ABM is technically simple, it is also conceptually deep. This unusual combination often leads to improper use of ABM.

Benefits of Agent-Based Modeling.

The benefits of ABM over other modeling techniques can be captured in three statements: (i) ABM captures emergent phenomena; (ii) ABM provides a natural description of a system; and (iii) ABM is flexible. It is clear, however, that the ability of ABM to deal with emergent phenomena is what drives the other benefits.

ABM captures emergent phenomena.

Emergent phenomena result from the interactions of individual entities. By definition, they cannot be reduced to the system's parts: the whole is more than the sum of its parts because of the interactions between the parts. An emergent phenomenon can have properties that are decoupled from the properties of the part. For example, a traffic jam, which results from the behavior of and interactions between individual vehicle drivers, may be moving in the direction opposite that of the cars that cause it. This characteristic of emergent phenomena makes them difficult to understand and predict: emergent phenomena can be counterintuitive. Numerous examples of counterintuitive emergent phenomena will be described in the following sections. ABM is, by its very nature, the canonical approach to modeling emergent phenomena: in ABM, one models and simulates the behavior of the system's constituent units (the agents) and their interactions, capturing emergence from the bottom up when the simulation is run.

Here is a simple example of an emergent phenomenon involving humans. It is a game that is easy to play with a group of 10–40 people. One asks each member of the audience to randomly select two individuals, person A and person B. One then asks them to move so they always keep A between them and B so A is their protector from B. Everyone in the room will mill about in a seemingly random fashion and will soon begin to ask why they are doing this. One then asks them to move so that they keep themselves in between A and B (they are the Protector). The results are striking: almost instantaneously the whole room will implode, with everyone clustering in a tight knot. This example shows how simple individual rules can lead to coherent group behavior, how small changes in those rules can have a dramatic impact on the group behavior, and how intuition can be a very poor guide to outcomes beyond a very limited level of complexity. The group's collective behavior is an emergent phenomenon. By using a simple agent-based simulation (available at www.icosystem.com/game.htm) in which each person is modeled as an autonomous agent following the rules, one can actually predict the emerging collective behavior. Although this is a simple example, where individual behavior does not change over time, ABM enables one to deal with more complex individual behavior, including learning and adaptation.

One may want to use ABM when there is potential for emergent phenomena, i.e., when:

• Individual behavior is nonlinear and can be characterized by thresholds, if-then rules, or nonlinear coupling. Describing discontinuity in individual behavior is difficult with differential equations.

• Individual behavior exhibits memory, path-dependence, and hysteresis, non-markovian behavior, or temporal correlations, including learning and adaptation.

• Agent interactions are heterogeneous and can generate network effects. Aggregate flow equations usually assume global homogeneous mixing, but the topology of the interaction network can lead to significant deviations from predicted aggregate behavior.

• Averages will not work. Aggregate differential equations tend to smooth out fluctuations, not ABM, which is important because under certain conditions, fluctuations can be amplified: the system is linearly stable but unstable to larger perturbations.

Interestingly, because ABM generates emergent phenomena from the bottom up, it raises the issue of what constitutes an explanation of such a phenomenon. The broader agenda of the ABM community is to advocate a new way of approaching social phenomena, not from a traditional modeling perspective but from the perspective of redefining the scientific process entirely. According to Epstein and Axtell (1), “[ABM] may change the way we think about explanation in the social sciences. What constitutes an explanation of an observed social phenomenon? Perhaps one day people will interpret the question, ‘Can you explain it?’ as asking ‘Can you grow it?’.”

ABM provides a natural description of a system.

In many cases, ABM is most natural for describing and simulating a system composed of “behavioral” entities. Whether one is attempting to describe a traffic jam, the stock market, voters, or how an organization works, ABM makes the model seem closer to reality. For example, it is more natural to describe how shoppers move in a supermarket than to come up with the equations that govern the dynamics of the density of shoppers. Because the density equations result from the behavior of shoppers, the ABM approach will also enable the user to study aggregate properties. ABM also makes it possible to realize the full potential of the data a company may have about its customers: panel data and customer surveys provide information about what real people actually do. Knowing the actual shopping basket of a customer makes it possible to create a virtual agent with that shopping basket rather than a density of people with a synthetic shopping basket computed from averaging over shopping data.

The difference between business processes and activities provides another example of how much more natural ABM is. A business process is an abstraction, sometimes useful, which is often difficult for people inside an organization to relate to. ABM looks at the organization from the viewpoint not of business processes but of activities, that is, what people inside the organization actually do (Fig. 1).

Fig. 1.

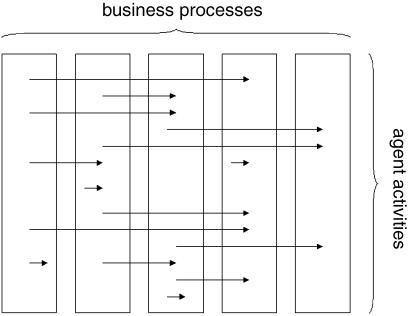
Illustration of the business process and agent views of a business.

The two descriptions must, of course, be mutually consistent. The business process description actually provides the modeler with a useful consistency check. However, when it comes to populating, validating, and calibrating the model, people inside the organization have an easier time answering questions about their own activities: they can relate to the model because the models describes their activities.

One may want to use ABM when describing the system from the perspective of its constituent units' activities is more natural, i.e., when:

• The behavior of individuals cannot be clearly defined through aggregate transition rates.

• Individual behavior is complex. Everything can be done with equations, in principle, but the complexity of differential equations increases exponentially as the complexity of behavior increases. Describing complex individual behavior with equations becomes intractable.

• Activities are a more natural way of describing the system than processes.

• Validation and calibration of the model through expert judgment is crucial. ABM is often the most appropriate way of describing what is actually happening in the real world, and the experts can easily “connect” to the model and have a feeling of “ownership.”

• Stochasticity applies to the agents' behavior. With ABM, sources of randomness are applied to the right places as opposed to a noise term added more or less arbitrarily to an aggregate equation.

ABM is flexible.

The flexibility of ABM can be observed along multiple dimensions. For example, it is easy to add more agents to an agent-based model. ABM also provides a natural framework for tuning the complexity of the agents: behavior, degree of rationality, ability to learn and evolve, and rules of interactions. Another dimension of flexibility is the ability to change levels of description and aggregation: one can easily play with aggregate agents, subgroups of agents, and single agents, with different levels of description coexisting in a given model. One may want to use ABM when the appropriate level of description or complexity is not known ahead of time and finding it requires some tinkering.

Areas of Application.

Examples of emergent phenomena abound in the social, political, and economic sciences. It has become progressively accepted that some phenomena can be difficult to predict and even counterintuitive. In a business context, situations of interest where emergent phenomena may arise can be classified into four areas:

1. Flows: evacuation, traffic, and customer flow management.

2. Markets: stock market, shopbots and software agents, and strategic simulation.

3. Organizations: operational risk and organizational design.

4. Diffusion: diffusion of innovation and adoption dynamics.

The rest of the article is organized around these areas of application.

Flows

Evacuation.

Crowd stampedes induced by panic often lead to fatalities as people are crushed or trampled. Such phenomena may be triggered in life-threatening situations such as fires in crowded buildings or may arise from the rush for seats or sometimes seemingly without causes. Recent examples include the panics in Harare, Zimbabwe, and at the Roskilde rock concert in Denmark. The frequency of such disasters seems to be increasing as growing population densities combined with easier transportation lead to greater mass events such as pop concerts, sporting events, and demonstrations. Panicking people are obsessed by short-term personal interests uncontrolled by social and cultural constraints. The reduced attention in situations of fear also causes such alternatives as side exits to be mostly ignored. In addition, there is social contagion, that is, a transition from individual to mass psychology, in which individuals transfer control over their actions to others, leading to conformity. Such irrational herding behavior often leads to bad overall results such as dangerous overcrowding and slower escape, increasing the fatalities or, more generally, the damage. In agent terms, collective panic behavior is an emergent phenomenon that results from relatively complex individual-level behavior and interactions between individuals (hypnotic effect, mutual excitation of a primordial instinct, circular reactions, and social facilitation). ABM seems ideally suited to provide valuable insights into the mechanisms of and preconditions for panic and jamming by in-coordination. Simulation results (4, 5) suggest practical ways of minimizing the harmful consequences of such events and the existence of an optimal escape strategy. For example, let us consider a fire escape situation in a confined space: a movie theatre or a concert hall. Let us assume that there is one exit available. How can one increase the outflow of people? Narrowing down the problem, one could ask: what is the effect of putting a column (a pillar) just before exit, slightly asymmetrically (for example, to the left of the exit), about 1 m away from the exit? Intuitively, one might think the column will slow down the outflow of people. However, ABM, backed by real-world experiments, indicates that the column regulates the flow, leading to fewer injured people and a significant increase in the flow, especially if one assumes that injured people cannot move and impede the flow (4). This result is an example of a counterintuitive consequence of an emergent phenomena: who would think of putting a column in front of an emergency exit? ABM captures that emergent phenomenon in a natural way (Fig. 2).

Fig. 2.

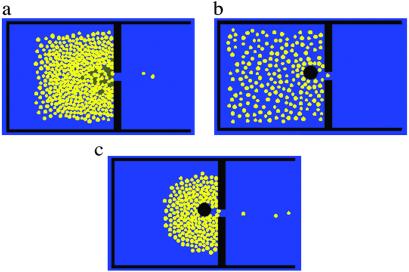
Fire escape agent-based simulation (live simulation available at www.helbing.org). People are represented by circles, green circles being injured people. Simulations assume 200 people in a room. (a) No column. (b) With column, after 10 s. (c) With column, after 20 s. In the absence of the column, 44 people escape and 5 are injured after 45 s; with the column, 72 people escape and no one is injured after 45 s. After Helbing et al. (4).

Flow Management.

An obvious flow management application of ABM is traffic. One of the most ambitious modeling projects in this area has been under way at the Los Alamos National Laboratory (LANL) for several years (transims.tsasa.lanl.gov). A team from LANL's Technology and Safety Assessment Division has developed a traffic simulation software package to create products that can be deployed to metropolitan planning agencies nationwide. The TRansportation ANalysis SIMulation System (TRANSIMS) ABM package provides planners with a synthetic population's daily activity patterns (such as travel to work, shop, and recreation, etc.), simulates the movements of individual vehicles on a regional transportation network, and estimates air pollution emissions generated by vehicle movements. Travel information is derived from actual census and survey data for specific tracts in target cities, providing a more accurate sense of the movements and daily routines of real people as they negotiate a full day with various transportation options available to them. TRANSIMS is based on (and contributes to the further development of) advanced computer simulation codes developed by Lawrence Livermore National Laboratory for military applications. TRANSIMS models create a virtual metropolitan region with a complete representation of the region's individuals, their activities, and the transportation infrastructure. Trips are planned to satisfy the individuals' activity patterns. TRANSIMS then simulates the movement of individuals across the transportation network, including their use of vehicles such as cars or buses, on a second-by-second basis. This virtual world of travelers mimics the traveling and driving behavior of real people in the region. The interactions of individual vehicles produce realistic traffic dynamics from which analysts using TRANSIMS can estimate vehicle emissions and judge the overall performance of the transportation system. Previous transportation planning surveyed people about elements of their trips such as origins, destinations, routes, timing, and forms of transportation used, or modes. TRANSIMS starts with data about people's activities and the trips they take to carry out those activities, then builds a model of household and activity demand. The model forecasts how changes in transportation policy or infrastructure might affect those activities and trips. TRANSIMS tries to capture every important interaction between travel subsystems, such as an individual's activity plans and congestion on the transportation system. For instance, when a trip takes too long, people find other routes, change from car to bus or vice versa, leave at different times, or decide not to engage in a certain activity at a given location. Also, because TRANSIMS tracks individual travelers—locations, routes, modes taken, and how well their travel plans are executed—it can evaluate transportation alternatives and reliability to determine who might benefit and who might be adversely affected by transportation changes. In the initial case studies, a 25-square-mile portion of the Dallas/Fort Worth region was used for demonstrating the first TRANSIMS version. Using existing Dallas/Fort Worth production/attraction zonal data, activities, and plans for ≈3.5 million travelers were generated for the hours of 5:00–10:00 a.m. Of these plans, those falling within a 25-square-mile study region were used as input to the simulation module to compare two infrastructure changes with respect to how each helped alleviate congestion. Although both alternatives improved congested conditions and flow along the freeway, an unexpected result was that the alternative of improving local arterials was superior to the alternative of adding lanes to the freeway from the perspective of network reliability. Network reliability is a measure of day-to-day variability in travel times experienced by travelers. In other words, if it takes one anywhere from 10 to 30 min to drive to work, network reliability is low; if it takes one between 10 and 12 min, network reliability is high. The team has recently been simulating the metropolitan region of Portland, OR, a model that requires 120,000 links and 1.5 million travelers, an order of magnitude larger than the Dallas/Fort Worth simulation of 10,000 links and 200,000 travelers. The benefits of the ABM approach are obvious: better and more efficient infrastructure planning, including not only better throughput but also compliance in terms of emissions, enabled by the ability of ABM to capture and reproduce emergent traffic phenomena.

Another application of ABM to flow management is the simulation of customer behavior in a theme park or supermarket. The collective patterns generated by thousands of customers can be extremely complex as customers interact: for example, how long one waits at an attraction in a theme park depends on other people's choices. A major theme park resort company was thinking about how to improve adaptability in labor scheduling, but knew that this depended on knowing more about the optimal balance of capacity and demand. Axtell and Epstein developed ResortScape (13), an agent-based model of the park that provides an integrated picture of the environment and all of the interacting elements that come into play in such a resort. The model provides a fast in silico way for managers to identify, adjust, and watch the impact of any number of management levers such as:

• When or whether to turn off a particular ride.

• How to distribute rides per capita throughout the park space.

• What is the tolerance level for wait times.

• When to extend operating hours.

In the simulation, agents represent a realistic and changeable mix of both supply (attractions, shops, food concessions) and demand (visitors with different preferences) elements of a day at the park. Leveraging existing resources and data, such as customer surveys, segmentation studies, queue timers, people counters, attendance estimates, and capacity figures, the model generates information about guest flow. Users can design and run an infinite number of scenarios to study the dynamics of the park space, test the effectiveness of various management decisions, and track visitor satisfaction throughout the day.

ABM is particularly useful in this context, because the mapping between the agents' preferences and behaviors on the one hand, and the park's performance (in terms of average waiting times, number of attractions visited, total distance walked, etc.) on the other is too complex to be dealt with by using mathematical techniques and purely statistical analysis of the data. Why is the mapping too complex? Because, for example, the time a given customer has to wait at a given attraction depends on what other customers are doing, how they respond to different park conditions, what their wish list is, etc. The flow of customers in the park and the money they spend are “emergent” properties of interactions among and between customers and the spatial layout of the park. Therefore, simulating the park's operations with a given layout seems to be the only solution. ABM is the most natural and easiest way of describing the system, because the actors of this system are customers (and attractions) with a behavior of their own. For example, waiting times at a theme park attraction result from the interactions of many behavioral units: the customers. Finally, the data available to the modeler are naturally structured for ABM: the available data are a description of the desires and behaviors of a number of customers.

Along the same lines, Bilge, Venables, and Casti have developed an agent-based model of a supermarket (www.simworld.co.uk) (6). SimStore is a model of a real British supermarket, the Sainsbury's store at South Ruislip in West London. The agents in SimStore are software shoppers armed with shopping lists. They make their way around the silicon store, picking goods off the shelves according to rules such as the nearest-neighbor principle: “Wherever you are now, go to the location of the nearest item on your shopping list.” Using these rules, SimStore generates the paths taken by customers, from which it can calculate customer densities at each location.

It is also possible to link all points visited by, say, at least 30% of customers to form a most popular path. An optimization algorithm can then change where in the supermarket different goods are stacked and so minimize, or maximize, the length of the average shopping path. Shoppers, of course, do not want to waste time, so they want the shortest path. But the store manager would like to have them pass by almost every shelf to encourage impulse buying. So there is a dynamic tension between the minimal and maximal shopping paths. This model was originally aimed at helping Sainsbury's to redesign its stores to generate greater customer throughput, reduce inventories, and shorten the time that products are on the shelves.

Macy's is a department store chain using ABM (7). In 1997, Macy's East approached PricewaterhouseCoopers with the following question: “How do we know when we have the right number of salespeople on the selling floor?” According to industry veterans, the retail business is a business of averages, where analysis is done on a spreadsheet. It is a business that deals with sales volume per hour as the determining factor in its allocation of salespeople, and the number of salespeople placed on the selling floor is based on the velocity in sales predicted for a specific day. And yet real behavior is the result of interactions between individuals, not averages. With ABM, Macy's had the opportunity to use visualization to review data in a way that becomes informational and leads to solutions. Spreadsheet data averages can be used to estimate distributions of individual behavior, so the individual agents in the simulation are consistent with the available real-world data. But because the agents represent individuals, the actual flow of their behavior can be much more realistic and informative. So instead of making estimates from the top down, Macy's can observe how volume really occurs from the bottom up. The virtual store can be modified in terms of layout (shelves, cash register positions, gates, etc.) and number of employees per department to see how these changes influence the affective state of a large number of agents. One can then explore the space of levers to maximize the number of happy customers in the most cost-effective way. Results from the model include the observation of “microbursts” of demand, where customers may be doing “project shopping” (e.g., buying an outfit and then accessorizing it), the importance of proximity to items (physical placement as well as brand-relatedness), which helps drive impulse buying.

Markets

The dynamics of the stock market results from the behavior of many interacting agents, leading to emergent phenomena that are best understood by using a bottom-up approach—ABM. There has been an upsurge of interest in agent-based models of markets in the last few years, stimulated by the pioneering work of Arthur and colleagues (8, 9). One commercial application has been developed by Bios Group for the National Association of Security Dealers Automated Quotation (NASDAQ) Stock Market (www.cbi.cgey.com/journal/issue4/features/future/future.pdf). In 1997, the NASDAQ Stock Market was about to implement a sequence of apparently small changes: reduction in tick size, from 1/8th to 1/16th and so on down to pennies. NASDAQ considers changes in trading policies very carefully: NASDAQ stands to lose a great deal if a new rule provokes a negative network-wide response from investors, market makers, and issuers. In the past, NASDAQ executives have analyzed the financial marketplace through economic studies, financial models, and feedback from market participants. The Market Quality Committee establishes regulations largely as a result of input from economists, lawyers, lobbyists, and policy makers.

To evaluate the impact of tick-size reduction, NASDAQ has been using an agent-based model that simulates the impact of regulatory changes on the financial market under various conditions. The model allows regulators to test and predict the effects of different strategies, observe the behavior of agents in response to changes, and monitor developments, providing advance warning of unintended consequences of newly implemented regulations faster than real time and without risking early tests in the real marketplace. In the agent-based NASDAQ model, market maker and investor agents (institutional investors, pension funds, day traders, and casual investors) buy and sell shares by using various strategies. The agents' access to price and volume information approximates that in the real-world market, and their behaviors range from very simple to complicated learning strategies. Neural networks, reinforcement learning, and other artificial intelligence techniques were used to generate strategies for agents. This creative element is important because NASDAQ regulators are especially interested in strategies that have not yet been discovered by players in the real market, again to approach their goal of designing a regulatory structure with as few loopholes as possible, to prevent abuses by devious players.

The model produced some unexpected results. Specifically, the simulation suggests a reduction in the market's tick size can reduce the market's ability to perform price discovery, leading to an increase in the bid–ask spread. A spread increase in response to tick-size reduction is counterintuitive because tick size is the lower bound on the spread. Initially, it was believed that the implementation of decimalization would be conducive to tighter spread, easing the discrepancy between bids and asking prices. Decimalization, overall, was thought to be highly efficient and effective. Among market professionals, the perceived wisdom is that providing greater granularity of price denomination is good for investors because it promotes competition among buyers and sellers who can negotiate in more precise terms, and thus it drives the market's spread down, which results in better prices for investors. This wisdom is difficult to test empirically: the complexity of market behavior makes isolating cause and effect highly problematic. Without a computer simulation, rule makers are stuck with an intuitive argument, and one that is poor in detail, judging market interaction by only one measure: competition (and hence price). Other dimensions of the problem go unaddressed: if better prices are available, do only small investors benefit, or will large ones benefit too? Will smaller tick sizes make the market more jittery and volatile?

A spreadsheet model or even system dynamics (10) (a popular business-modeling technique that uses sets of differential equations) would not have been able to generate the same deep insights as ABM, because the behavior of the market emerges out of the interactions of the players, who in turn may change their behavior in response to changes in the market. The interactions between investors, market makers, and the operating rules of the NASDAQ Stock Market make the entire system's dynamics quite hard to understand. Predicting how it would change under a new set of operating regulations cannot be based on intuition or on classical modeling techniques, because they are not suited to describe the complexities of the behavior of the stock market agents. For example, the mapping between tick size and spread can be understood only by taking into account details of the investors' and market makers' behavior to model the process of price discovery.

Stock markets are not the only markets that can be better understood by using ABM. For example, auctions can benefit from the approach. Indeed, electronic double auctions using intelligent agents have many applications today. eBay uses intelligent agents to allow customers to automate the bidding process, but these could be made much more sophisticated by using ABM to test a variety of robot behaviors. Designing intelligent agents that have desired aggregate properties could turn out to be the “killer app” that will make the cyber world the preferred medium for economic transactions. Shopbots are Internet agents that automatically search for information that pertains to the price and quality of goods and services. As the prevalence of shopbots in electronic commerce increases, the resultant reduction in economic friction because of decreased search costs could dramatically alter market behavior. Some predict that intelligent agents eventually will transform our world, which means they may trade information, gather information, translate information, and perform all sorts of negotiations for us in the future. Ultimately, transactions among economic software agents will constitute an essential and perhaps even dominant portion of the world economy. It is tempting to assume that the same mechanisms can be applied successfully to software agents. But one must be very careful about the introduction of agent technology, as agents behave in a way that is still poorly understood. For example, in an all-agent auction, prices tend to rise, reach a peak, and then suddenly dip dramatically before the same process begins again. IBM's Kephart and his colleagues have been exploring the potential impact of shopbots on market dynamics, by simulating and analyzing an agent-based model of shopbot economics, which incorporates software agent representations of buyers and sellers (11). Their model is similar to some that are studied by economists interested, for example, in the phenomenon of price dispersion, with different underlying assumptions and methodology: here the goal is to design economic software agents, rather than “just” explain human economic behavior. In particular, they have been examining agent economies in which (i) search costs are nonlinear; (ii) some portion of the buyer population makes no use of search mechanisms; and (iii) shopbots are economically motivated, strategically pricing their information services so as to maximize their own profits. Under these conditions, they have found that markets can exhibit a variety of hitherto unobserved dynamical behaviors, including complex limit cycles and the coexistence of multiple buyer search strategies. A shopbot that charges buyers for price information can manipulate markets to its own advantage, sometimes inadvertently benefiting buyers and sellers.

The same ABM techniques that are used to study the stock market or the collective behavior of shopbots can be applied to situations where there are many agents playing economic games. That is “game theory without the theory.” Game theory is a great framework, but game theorists suffer from self-imposed constraints: being able to prove theorems puts severe limitations to what is possible. In particular, any realistic situation is likely to lie beyond the grasp of theory. Axelrod (2) argues that agent-based game theory is the only way forward.

A team at Icosystem Corporation has simulated the Internet service provider (ISP) market with ABM (www.icosystem.com). The agents are used to represent both the ISPs and their customers. Each ISP is an agent and each customer is an agent. The ISPs' offerings are confronted with customers' needs and expectations; customers make decisions (to adopt, leave, or switch) depending on the match between their profiles and the ISPs'. One of the attributes of the ISPs, among may others, is how much they charge monthly for their services. ISPs that do not make enough money are eliminated following an “evolutionary” dynamics; those that are successful give rise to copycats (that is, ISPs with similar business models) and also fine tune their own business models. ABM produced two significant results: (i) It discovered the free ISP business model (no monthly fee). (ii) It predicted the instability of the free ISP business model: the first free ISP that emerges in the simulation differentiates itself from the pack by providing services without charging monthly fees and making money on advertising. These two properties emerge out of the interaction dynamics between the ISPs through the marketplace. Because ISPs learn and evolve, it would have been difficult to obtain this insight by using other simulation methods.

Organizations

One promising area of application for ABM is organizational simulation (12). It is clearly possible to model the emergent collective behavior of an organization or of a part of an organization in a certain context or at a certain level of description. At the very least, the process of designing the simulation produces valuable qualitative insights. But, in certain cases, one is also able to generate semiquantitative insights. A good illustration of this is an agent-based model of operational risk (www.businessinnovation.ey.com/events/pubconf/2000–04-28/ec5transcripts/BonabeauNivollet.pdf) (13).

A human organization is often subject to operational risk. Consider financial institutions. Operational risk arises from the potential that inadequate information systems, operational problems, breaches in internal controls, fraud, or unforeseen catastrophes will result in unexpected losses. According to the Basle Committee on Banking, operational risk involves breakdowns in internal controls and corporate governance that can lead to financial losses through error, fraud, or failure to perform in a timely manner or cause the interests of the bank to be compromised in some other way, for example, by its dealers, lending officers, or other staff exceeding their authority or conducting business in an unethical or risky manner. It is increasingly viewed as the most important risk that banks face. Examples of large operational losses include Daiwa, Sumitomo, Barings, Salomon, Kidder Peabody, Orange County, Jardine Fleming, and more recently NatWest Markets, the Common Fund, or Yamaichi. Although most banks have developed efficient and sometimes sophisticated ways of dealing with market risk and to large extent credit risk, they are still in the early stages of developing operational risk measurement and monitoring. Unlike market and credit risk, operational risk factors are largely internal to the organization, and a clear mathematical or statistical link between individual risk factors and the size and frequency of operational loss does not exist. Experience with large losses is infrequent, and many banks lack a time series of historical data on their own operational losses and their causes. Uncertainty about which factors are important arises from the absence of a direct relationship between the risk factors usually identified (measured through internal audit ratings, internal control self-assessment based on such indicators as volume, turnover, error rates, and income volatility) and the size and frequency of loss events. This contrasts with market risk, where changes in prices have an easily computed impact on the value of the bank's trading portfolio, and with credit risk, where changes in the borrower's credit quality are often associated with changes in the interest rate spread of the borrower's obligations over a risk-free rate. Given all of the characteristics of operational risk, it is obviously difficult to quantify. Operational historical data are so scarce that it is not possible to allocate capital reliably and efficiently, and it is not possible to obtain good VAR (value-at-risk) and RAROC (risk-adjusted return on capital) estimates. Capital allocation is important because it gives managers an incentive to keep operational risk under control. Yet there is increasing pressure on financial institutions to quantify operational risk in a way that convinces both investors (efficient allocation of capital) and regulatory entities (risk under “control”). More precisely, a financial institution must be able to quantify operational risk within a reliable framework to be able to keep risk under control, optimize economic capital allocation, and determine its insurance needs.

Given the characteristics of operational risk, bottom-up enterprise-wide simulation looks like a promising approach (to low-frequency high-impact operational risk). What is needed is a framework that includes the possibility of nonlinear effects because of interactions among subunits and to cascading events. The framework should be able to operate with scarce data. Hence the idea to simulate operations from the bottom up to generate a large artificial data set that includes large events. The artificially generated data can then be used to apply classical capital allocation techniques. Bios and Cap Gemini Ernst & Young (13) have applied ABM techniques to measuring and managing operational risk at Société Générale Asset Management (SGAM). A simulation model of the business unit's activities was designed, starting with business process modeling and workflow identification. By using the business process model and the workflows the bank's “agents” were then identified, and their activities were modeled as well as their interactions with other agents and the risk factors that could impact their activities. To make the tool tractable in the end the activities had to be modeled in enough detail to capture the “physics” of the bank but not too much detail. The risk factors were connected to the bank's profit and loss through potentially complex pathways in the organization, for example from a client's order to the detection of a trading error in the back office. Then the bank's environment was modeled—the markets, customers, regulators, etc. By running the model, it is possible to generate artificial earnings distributions, used to estimate potential losses and their likelihood. For example, the bank can compute its “earnings-at-risk,” that is, the minimum earnings that could be observed in one year at the bank with a 95% level of confidence. The benefit to the bank: its allocation of economic capital is backed by a simulation of how the organization operates rather than based on some strange combination of industry-wide historical data and accounting magic. If the model is good, regulators accept it more easily and the bank does not have to put aside 10 times the amount of economic capital it really needs. For an asset management business, economic capital is a fraction of assets under management. Reducing the fraction by just 0.01% means millions of dollars. Measuring is just the first step, though. An added benefit of simulation is that one can identify where losses come from and test mitigation procedures.

When deciding to model a bank by using ABM, one is not making an arbitrary modeling decision. One is modeling the bank in a way that is natural to the practitioners, because one is modeling the activities of the bank by looking at what every actor does. If one is modeling the bank's processes instead, it is more difficult for people to understand the model because one person's activities span many processes. That has important consequences when it comes to populating, validating, and calibrating the model. If people “connect” to the simulation model, in the sense that they recognize and understand what the model is doing, they can improve it, more easily quantify what needs to be quantified, etc. Because they have a deep understanding of the risk drivers related to their own activity, it is easier to incorporate the relevant risk drivers into the model. Once they have their activities and the corresponding risk drivers in the model, they can suggest control and mitigation procedures and test them by using the simulation tool. In other words, ABM is not only a simulation tool; it is a naturally structured repository for self-assessment and ideas for redesigning the organization.

ABM is perfect not just for operational risk in financial institution but for modeling risk in general. Modeling risk in an organization using ABM is THE right approach to modeling risk because most often risk is a property of the actors in the organization: risk events impact people's activities, not processes. For example, it is more natural to say that someone in accounting made a mistake (sent the wrong invoice to a customer) than to say the receivables process was impacted by an error event in the invoicing subprocess. ABM will revolutionize business risk advisory services because it constitutes a paradigm shift from spreadsheet-based and process-oriented models. Populating, validating, and calibrating an agent-based model of risk is an order of magnitude easier and makes much more sense than other models. The agent-based model also makes the formulation of mitigation strategies easier. Within 3–6 years, ABM should be used routinely in audit.

What the Société Générale Asset Management example has hinted at is the idea of using ABM to design better organizations (12). Indeed, once one has a reliable model of an organization, it is possible to play with it, change some of the organizational parameters, and measure how the performance of the organization varies in response to these changes. Performance measurements can range from how fast information propagates in the organization to how good the organization is at collectively performing its task—inventing new products, selling, or managing receivables.

Diffusion

In the context of this section, ABM applies to cases where people are influenced by their social context, that is, what others around them do. Although a lot of academic attention has been given to the subject, there are very few business applications, perhaps because of the “soft” nature of the variables and the difficulty in measuring parameters. Social simulation in business has not been very successful so far, because the emphasis has been on using it as a predictive tool rather than as a learning tool. For example, a manager can understand her marketplace better by playing with an agent-based model of it. Then, of course, quantifying the tangible benefits of something intangible is difficult, and a manager cannot claim to have saved $X million by playing with a simulation of her customers. Still, there is a lot of value in using social simulation in a business context. Farrell and his team developed a synthetic world populated by virtual agents to try to predict how (and when) hits happen (7). Working for Twentieth Century Fox, they modeled how such movies as “Titanic” or “The Blair Witch Project” could become hits, but their model was not very successful. Predicting hits might be the single most difficult thing to do; understanding how hits happen is a better use of the model.

Let us examine a simple product adoption model to illustrate the value of ABM in modeling diffusion on social networks. This example will also show why and when ABM is needed and will highlight the relationship between ABM and a more traditional aggregate system dynamics model (10). Let us assume a new product's value V depends on the number of its users, N, in a total population of N_T potential adopters, according to the following function

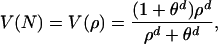where ρ is the fraction of the population that has adopted the product, θ is a characteristic value (here θ = 0.4), and d is an exponent that determines the steepness of the function (here d = 4). V(N) equals 0 when there is no user and is maximum (= 1) when the entire population has adopted the product. Finally, θ acts as a threshold: when the user base approaches 40% of the population, the value curve takes off. Let us assume for simplicity that the value function is the same for all users. Let us further assume that the adoption rate is given by an estimate of V by potential customers. Indeed, customers may not know the exact number of people who have adopted the technology in the population, but they can estimate the fraction of users in their social neighborhood. If we assume that each person is connected to n other people in the population, we can define person k's estimate of the fraction of users in the entire population as ρ̂_k = n_k/n, where n_k is the number of k's neighbors who have adopted the product. The value V̂_k of the product, as estimated by person k, is then given by

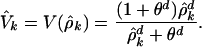If person k is connected to everyone else, V̂_k is identical to V. However, that is unlikely. A system dynamics approach to the problem would model the flow of people from nonusers to users, with every person in the population perceiving the same average fraction of adopters ρ = N/N_T and therefore the same perceived value:

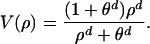The resulting differential equation is

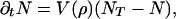which is equivalent to

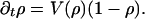We assume here that the time unit is 10 days. Fig. 3a shows how ρ and V vary in time, when the initial number of users is equal to 5% of the population.

Fig. 3.

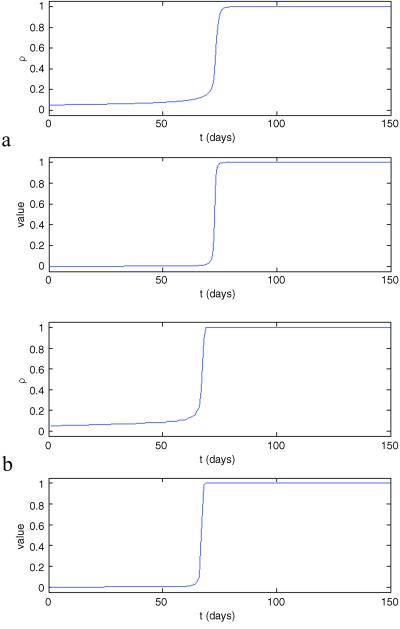
(a) Differential equation results. (b) Mean-field agent-based model.

Let us now consider how an agent-based approach would treat this problem. The first transformation is from the master equation (that is, the equation describing the dynamics of the total number of users) to individual transition probabilities, where each agent has a transition probability given by the rate of the master equation. In other words, for each agent who is not already a user, the probability of becoming one is equal to V(ρ) per time unit. The meaning of this model is that each agent acts individually but has perfect knowledge of how many users there are in the population. Fig. 3b shows how the fraction of users increases in time for a population of 100 agents. This curve is almost indistinguishable on average from that obtained with the system dynamics approach, except when the initial population of users is very low, in which case the takeoff can be significantly slower in the agent-based description in some simulations because of significant fluctuations in the early part of the simulation. These fluctuations reflect the individual decision-making by agents as opposed to an average global flow. Yet, on average, one obtains the same dynamics as the flow model. Things become quite different, however, as soon as one starts assuming that the agents estimate the fraction of users from the fraction of their neighbors who are users. Let us assume that each person in the population has exactly n = 30 neighbors. Let us now consider two cases:

1. Those 30 neighbors are selected randomly in the population.

2. There is clustering in the topology of social interactions in that a neighbor of a neighbor is likely to be a neighbor. For definiteness, I will assume that the population is divided into two subpopulations of equal size. The probability that two individuals from the same subpopulation are neighbors is equal to P = 0.5, and the probability that two individuals from different subpopulations are neighbors is equal to 0.1. In a population of 100 agents, the average total number of neighbors of any given node is 0.5⋅50 + 0.1⋅50 = 30. We assume that the initial 5% of users is within one of the subpopulations.

The second case introduces localization in the dynamics: a person interacts only with her neighbors and there are few long-range interactions and little global mixing. In the first case, one might expect to observe a dynamics similar to the system dynamics model, whereas the dynamics in the second case could be quite different. It appears that even in the first case the resulting dynamics is different from the mean-field dynamics (Fig. 4a), but the second case leads to potentially dramatically different results, as can be seen in Fig. 4b. Product adoption is a lot faster with clustering, even when the initial user population is located entirely within one cluster.

Fig. 4.

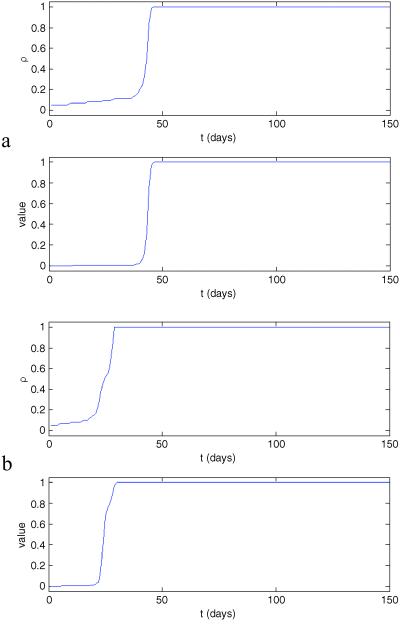
(a) One hundred agents, 30 random neighbors. (b) One hundred agents, clustered neighbors (two clusters, spread starting in one cluster).

This simple example shows not only how useful ABM is when dealing with inhomogeneous populations and interaction networks but also how to go from a differential equation model to an agent-based model—usually it is the opposite transformation that is used, where the differential equation model is the analytically tractable (but deceivingly so) mean-field version of the agent-based model. What is useful about this “reverse” transformation is that it clearly shows that an agent-based model is increasingly necessary as the degree of inhomogeneity increases in the modeled system.

Discussion

When Is ABM Useful?

It should be clear from the examples presented in this article that ABM can bring significant benefits when applied to human systems. It is useful at this point to summarize when it is best to use ABM:

• When the interactions between the agents are complex, nonlinear, discontinuous, or discrete (for example, when the behavior of an agent can be altered dramatically, even discontinuously, by other agents). Example: all examples described in this article.

• When space is crucial and the agents' positions are not fixed. Example: fire escape, theme park, supermarket, traffic.

• When the population is heterogeneous, when each individual is (potentially) different. Example: virtually every example in this article.

• When the topology of the interactions is heterogeneous and complex. Example: when interactions are homogeneous and globally mixing, there is no need for agent-based simulation, but social networks are rarely homogeneous, they are characterized by clusters, leading to deviations from the average behavior.

• When the agents exhibit complex behavior, including learning and adaptation. Example: NASDAQ, ISPs.

Issues with ABM.

There are some issues related to the application of ABM to the social, political, and economic sciences. One issue is common to all modeling techniques: a model has to serve a purpose; a general-purpose model cannot work. The model has to be built at the right level of description, with just the right amount of detail to serve its purpose; this remains an art more than a science.

Another issue has to do with the very nature of the systems one is modeling with ABM in the social sciences: they most often involve human agents, with potentially irrational behavior, subjective choices, and complex psychology—in other words, soft factors, difficult to quantify, calibrate, and sometimes justify. Although this may constitute a major source of problems in interpreting the outcomes of simulations, it is fair to say that in most cases ABM is simply the only game in town to deal with such situations. Having said that, one must be careful, then, in how one uses ABM: for example, one must not make decisions on the basis of the quantitative outcome of a simulation that should be interpreted purely at the qualitative level. Because of the varying degree of accuracy and completeness in the input to the model (data, expertise, etc.), the nature of the output is similarly varied, ranging from purely qualitative insights all the way to quantitative results usable for decision-making and implementation.

The last major issue in ABM is a practical issue that must not be overlooked. By definition, ABM looks at a system not at the aggregate level but at the level of its constituent units. Although the aggregate level could perhaps be described with just a few equations of motion, the lower-level description involves describing the individual behavior of potentially many constituent units. Simulating the behavior of all of the units can be extremely computation intensive and therefore time consuming. Although computing power is still increasing at an impressive pace, the high computational requirements of ABM remain a problem when it comes to modeling large systems.

Abbreviations

• ABM, agent-based modeling

• NASDAQ, National Association of Security Dealers Automated Quotation

• ISP, Internet service provider