Determination of Antibiotic Effect in an In Vitro Pharmacodynamic Model: Comparison with an Established Animal Model of Infection

Abstract

Animal infection models have historically been used to study pharmacodynamic relationships. Similar results could theoretically be produced by using an in vitro pharmacodynamic model as an alternative to animal models. We compared the antibiotic effects of ticarcillin administered in various doses and dosing regimens against Pseudomonas aeruginosa ATCC 27853 under conditions analogous to those previously employed in a neutropenic-mouse thigh infection model (B. Vogelman et al., J. Infect. Dis. 158:831-847, 1988). Ticarcillin dosages of either 96, 192, or 384 mg/day were administered at 1-, 2-, 3-, 4-, 8-, 12-, or 24-h intervals into a two-compartment model in order to duplicate the concentration-time profiles of the animal model. Colony counts were enumerated at 0 and 24 h. Linear regression and sigmoidal maximum-effect (Emax) model fitting were used to assess the relationship between the percentage of time that the concentration remained above the MIC (%T>MIC) or above four times the MIC (%T>4×MIC) and the change in the log₁₀ CFU per milliliter (Δlog₁₀ CFU/ml) in the central and peripheral compartments. Statistical analysis of the Δlog₁₀ CFU/ml values was performed for matched regimens of the in vitro and animal models based on the %T>MICs. The slopes of the regression equations of %T>MICs relative to Δlog₁₀ CFU/ml values were similar for the in vitro and animal models, but the y intercept was greater with the in vitro model. The Δlog₁₀ CFU/ml values of the 0- to 24-h colony counts at equivalent %T>MICs in the two models were not statistically different (P = 0.087). Overall, the peripheral compartment of the in vitro model was a better predictor of effect than the central compartment. This study, which compares pharmacodynamic principles between an in vitro and an animal model, demonstrated similar relationships between %T>MICs and effects.

Knowledge of an antibiotic's pharmacodynamic and pharmacokinetic properties is necessary for the selection of the most appropriate dose and dosage regimen. While pharmacokinetics describes the time course of drug concentrations in relation to the dose or dosage regimen, pharmacodynamics describes the concentration-drug effect relationship and is time independent. Integration of the two allows a description of a drug's effect over time. While certain pharmacokinetic-pharmacodynamic relationships have been described for antibiotic classes based on both animal models and human data (e.g., time-dependent killing of bacteria with β-lactams and concentration-dependent killing of bacteria with aminoglycosides), it is difficult to assess individual agents relative to others from within and outside their chemical classes and thus to assess their relative activities and determine whether these characteristics vary with different bacteria. It would be practical and desirable to elucidate an antibiotic's concentration-effect-time course properties and characteristics in an in vitro model that precludes or minimizes the use of experimental animals or human trials early in the drug's development. While a number of in vitro pharmacodynamic models have been devised and described in the literature, none have been systematically compared to animal models to validate their use. The specific aims of the present study were designed to address this need by using a pharmacodynamic model developed in our laboratory.

Despite theories regarding the potential advantages of one in vitro model over others or over animal models, it is nonetheless unclear what relevance experimental results generated in these models has to human pharmacokinetics and pharmacodynamics and the treatment of clinical infection. It therefore appears logical, as a first step in addressing this issue, that results obtained from the in vitro model be compared with those obtained from an animal model under identical experimental conditions (i.e., the same antibiotic, equivalent doses and dosage regimens, the same test organism, and the same pharmacokinetic parameters). Thus, the objective of this study was to compare the antibacterial effect measured in an in vitro model with the published results of an established model, namely, thigh infections in neutropenic mice (21).

(This work has been presented in part at the 39th Interscience Conference on Antimicrobial Agents and Chemotherapy, San Francisco, Calif., 26 to 29 September 1999.)

MATERIALS AND METHODS

Antibiotics.

The antibiotic used in this study was pharmaceutical-grade ticarcillin disodium (lot numbers 30632DA and 48649DA; SmithKline Beecham Laboratories, Philadelphia, Pa.). Stock solutions of ticarcillin were prepared with sterile deionized water according to the manufacturer's directions prior to each model experiment. Analytical-grade ticarcillin disodium (lot number BN39; SmithKline Beecham Laboratories) was reconstituted in deionized water, and appropriate concentrations were prepared in cation-adjusted Mueller-Hinton broth for MIC testing and microbiologic assay.

Microorganisms and media.

The organism used in this experiment was Pseudomonas aeruginosa ATCC 27853 (American Type Culture Collection, Manassas, Va.). Mueller-Hinton broth (lot number 122488JD; Difco Laboratories, Detroit, Mich.) supplemented with CaCl₂ and MgCl₂ to produce final concentrations of 25 and 12.5 μg/ml, respectively, was prepared according to the National Committee for Clinical Laboratory Standards (NCCLS) guidelines (14). Ten-centimeter-diameter Mueller-Hinton II agar plates (lot numbers H5RKBF and I1RTMG; BBL, Cockeysville, Md.) were used for enumeration of the final inoculum and surviving colonies.

Microbiologic assay.

Ticarcillin concentrations from the central and peripheral compartments were quantitated in triplicate within 72 h by microbiologic assay. Bacillus subtilis ATCC 6633 was matched to a 0.5 McFarland standard in 0.9% saline and spread on 15-cm-diameter Mueller-Hinton agar plates (lot number H3RJUU; BBL). Twenty-microliter volumes of standard solutions (concentration range, 3 to 100 μg/ml) and unknowns were added to blank disks, placed on the agar plates, and incubated for 24 h at 35°C. Zones of inhibition were measured to the nearest 0.1 mm with a calibrating viewer (Transidyne General Corporation, Ann Arbor, Mich.). The standard curve was linear over a concentration range of 3 to 100 μg/ml (r² = 0.999), and the interday coefficient of variation was ≤3.6% at all concentrations.

MIC testing.

Broth microdilution MIC tests were conducted in accordance with the NCCLS guidelines (14) on eight replicates with cation-adjusted Mueller-Hinton broth. The modal MIC was used in subsequent pharmacodynamic calculations. The final inoculum was approximately 5 × 10⁵ CFU/ml and was verified in duplicate with a spiral plater (Spiral Systems, Cincinnati, Ohio). Microtiter trays were sealed and incubated for 18 h at 35°C in ambient air. The MIC was defined as the lowest concentration of antibiotic that prevented visual turbidity when a plate was examined with a magnified lighted microplate reader (Sensititre; Chelsea Instruments Ltd., Surrey, England).

In vitro model.

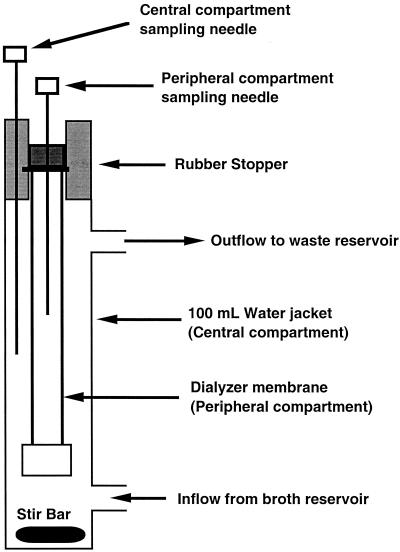
The in vitro model (Fig. 1) is comprised of a central compartment consisting of a dual-port 100-ml chromatography column water jacket into which a dialyzer (DispoDialyzer; Spectrum, Los Angeles, Calif.) is suspended from a rubber stopper. The dialyzer (peripheral compartment) holds approximately 6 ml of fluid. The dialyzer membrane is composed of a synthetic regenerated cellulose ester with a pore size of approximately 0.004 μm and an effective surface area-to-volume ratio of 5.34 cm⁻¹. Both the central and peripheral compartments of the model are fitted with needles for withdrawing samples. Fluid is circulated through the central compartment of the model via the lower water jacket port with a Masterflex multichannel, variable-occlusion cartridge head system and a computerized peristaltic pump and inert Masterflex silicone tubing (Cole-Parmer, Vernon Hills, Ill.). Antibiotics are also injected into the model via the lower port with a programmable syringe infusion pump (Medfusion, Inc., Duluth, Ga.). Fluid exits the model through the upper port by a gravity-dependent flow into a waste collection container.

FIG. 1.

In vitro pharmacodynamic model.

Preliminary experiments to characterize the in vitro model. (i) Concentration-time profile.

The concentration-time profiles of ticarcillin in the central and peripheral compartments were characterized for the in vitro model after the first dose and at steady state with daily doses ranging from 48 to 384 mg/day (equivalent to 600 to 4,800 mg per kg of body weight per day, respectively, in the animal model) in divided doses administered every 2 and 6 h. The peak concentration was defined as the concentration measured at the end of the infusion. The elimination-phase rate constant was defined as the negative slope of the terminal elimination phase as determined by least-squares linear regression. At least five concentration-time points were utilized in the calculation of the slope. The elimination-phase half-life was calculated by dividing 0.693 by the elimination phase rate constant, and the area under the concentration-time curve (AUC) was calculated by using the linear trapezoidal method. The percent penetration of ticarcillin into the peripheral compartment was calculated from the ratio of the AUC over a dosing interval (AUC_0-τ) in the peripheral compartment to the AUC_0-τ in the central compartment, where 0 indicates 0 h and τ is the end point of the dosing interval. Data from these studies were used to simulate the concentration-time profiles for subsequent experiments.

(ii) Growth control studies.

Control studies of the growth of P. aeruginosa ATCC 27853 in the peripheral compartment were performed to characterize growth in the in vitro model. In these studies, the organism was grown overnight on 10-cm-diameter Mueller-Hinton agar plates and then subcultured in cation-adjusted Mueller-Hinton broth and grown to mid-logarithmic phase (approximately 2 h). The culture was matched to a 0.5 MacFarland standard in sterile 0.9% saline by using the A-just system (Abbott Laboratories, North Chicago, Ill.) and was further diluted in cation-adjusted Mueller-Hinton broth prior to its introduction into the peripheral compartment. The peripheral compartment of each model was inoculated with 1 ml to produce a final inoculum of approximately 5 × 10⁵ CFU/ml and was incubated at 35°C. Duplicate samples were taken from each model at 0, 1, 2, 3, 4, 5, 6, 8, 12, and 24 h. Samples were serially 10-fold diluted in 0.9% saline and plated onto Mueller-Hinton agar plates with a spiral plater (Spiral Systems). For colony count determination, agar plates were incubated at 35°C for 18 h and colony counts were enumerated.

Comparison of in vitro and animal models.

P. aeruginosa ATCC 27853 was grown overnight on 10-cm-diameter Mueller-Hinton agar plates and then subcultured and grown to mid-logarithmic phase (approximately 2 h) in cation-adjusted Mueller-Hinton broth prior to its introduction into the peripheral compartment. Immediately prior to each experiment, the model was assembled under aseptic conditions, the central and peripheral compartments were filled with cation-adjusted Mueller-Hinton broth, and the models were allowed to equilibrate to 35°C for several hours. The flow rate of antibiotic-free cation-adjusted Mueller-Hinton broth through the model was adjusted to match the half-life of ticarcillin in mice under a corresponding regimen (the half-lives ranged from 15.0 to 29.7 min, depending on the dose). The inoculum was matched to a 0.5 McFarland standard in sterile 0.9% saline and then was further diluted with cation-adjusted Mueller-Hinton broth. One milliliter of the resulting suspension was then injected into the peripheral compartment to produce a final inoculum of approximately 5 × 10⁵ CFU/ml. One hour later, sampling for the inoculum at the start of the experiment (time zero) was performed in duplicate and the appropriate dose of ticarcillin was injected into the central compartment of the model over 1 min. The colony count of the starting (time zero) inoculum was used in the subsequent determination of antibiotic effect. Growth control experiments were performed simultaneously with these experiments.

Subsequent doses of ticarcillin were administered over 1 min with a programmable syringe infusion pump. The concentration of the antibiotic stock solutions was adjusted such that the administered antibiotic dose was delivered as a 1-ml injection. Doses were administered in the in vitro model in a manner that produced central compartment concentration-time profiles similar to the concentration-time profile in serum achieved with the murine model. The 24-h AUCs for the in vitro model central compartment were matched to the 24-h AUCs from the serum drug concentration-time curves for neutropenic mice with thigh infections (21). Thus, 24-h ticarcillin AUCs were approximately 480, 960, and 1,920 μg · h/ml. The drug doses required to achieve these 24-h AUCs were based on the volume in the central compartment of the in vitro model and the pump flow rate (drug clearance) and were fractionated by administration at intervals of 1, 2, 3, 4, 8, 12, and 24 h, with a total of 15 regimens tested (as opposed to 32 in the original animal studies). For the in vitro model, the doses, which were equivalent to those used for the animals, and dosing intervals studied were 1,200 mg/kg/day administered in fractions every 1, 2, 8, and 12 h; 2,400 mg/kg/day administered in fractions every 1, 2, 3, 4, 12, and 24 h; and 4,800 mg/kg/day administered in fractions every 1, 2, 4, 8, and 12 h. The dosage regimens used in the original animal studies and those duplicated here are presented in Table 1. These dosage regimens were originally selected to minimize interdependence among the following pharmacodynamic parameters: the AUC/MIC, the peak concentration/MIC, and the percentage of a time interval that the drug concentration remained above the MIC (%T>MIC). At 24 h after the initiation of drug exposure, duplicate aliquots were taken from the peripheral compartment for colony count determination. The aliquots were serially diluted in sterile 0.9% saline and plated onto Mueller-Hinton agar plates with a spiral plater. After incubation at 35°C under ambient atmospheric conditions for approximately 18 h, colony counts were enumerated. The limit of detection under these conditions was approximately 400 CFU/ml. To minimize the effect of antibiotic carryover from the 24-h samples, the aliquot removed from the peripheral compartment was first diluted in sterile 0.9% saline containing penicillinase (40,000 IU/ml; Difco) to inactivate any remaining ticarcillin. Each model experiment was performed in duplicate, and the means of the colony counts from the time zero and 24-h samples were used in the calculation of antibacterial activity.

TABLE 1.

Comparison of dosing regimens studied

Dose	Model	Dosing regimens used with a dosing interval (h) ofa:
		1	2	3	4	6	8	12	24
1,200 mg/kg/day	Animal	X	X	X	X	X	X	X	X
96 mg/day	In vitro	X	X				X	X
2,400 mg/kg/day	Animal	X	X	X	X	X	X	X	X
192 mg/day	In vitro	X	X	X	X			X	X
4,800 mg/kg/day	Animal	X	X	X	X	X	X	X	X
384 mg/day	In vitro	X	X		X		X	X

^aX indicates dosing regimens that were used with the indicated model.

Data analysis. (i) Antibacterial activity.

The change in log₁₀ CFU per milliliter over the 24-h treatment period (Δlog₁₀ CFU/ml) for each regimen in both the animal and in vitro models was calculated according to the equation Δlog₁₀ CFU/ml = 24-h log₁₀ CFU/ml − 0-h log₁₀ CFU/ml, where colony counts were mean values from duplicate animal or in vitro model experiments. Thus, negative Δlog₁₀ CFU/ml values were the result of fewer surviving colonies at 24 h than at time zero. In addition, the Δlog₁₀ CFU/ml for each regimen was converted to an effect by the equation Effect = Δlog₁₀ CFU/ml (max) − Δlog₁₀ CFU/ml (each regimen), where Δlog₁₀ CFU/ml (max) refers to the regimen with the largest positive Δlog₁₀ CFU/ml (the most regrowth or the greatest colony count at 24 h). By calculating an effect, a negative or positive Δlog₁₀ CFU/ml for each regimen was transformed into a positive value (ranging from 0 for the regimen demonstrating the least killing to the largest positive number for the regimen exhibiting the most killing).

(ii) Pharmacodynamic analysis.

The %T>MICs and percentages of a time interval that the concentration remained above four times the MIC (%T>4×MICs) in the central and peripheral compartments of the in vitro model were calculated by using the simulated concentration-time profiles for the specific regimens studied and the MIC as determined in our laboratory (16 μg/ml). All simulations were performed by using PharmaCalc software (version 1.0; Institut für Automatik, Zurich, Switzerland) with pharmacokinetic parameters elucidated in the preliminary experiments.

(iii) Pharmacodynamic relationships.

Linear regression was used to assess the relationship between the %T>MICs and the values for Δlog₁₀ CFU/ml for the central compartment of the in vitro and animal models and between the %T>4×MICs and the values for the Δlog₁₀ CFU/ml for the central and peripheral compartments of the in vitro model. In addition, the %T>MIC- and %T>4×MIC-effect relationships in the central (in vitro and animal models) and peripheral (in vitro model) compartments were characterized by fitting the data to a sigmoidal Emax model by using Boomer simulation and modeling software (version 2.6; David W. A. Bourne, Oklahoma City, Okla.) according to the following relationship: Effect = (Emax · Cⁿ)/(EC₅₀ + Cⁿ) where C refers to the %T>MIC or %T>4×MIC, n is the sigmoidicity factor, and EC₅₀ is the %T>MIC or %T>4×MIC at 50% of the Emax. The goodness of fit was assessed by using Akaike's information criterion (22), the sum of the weighted squared residuals, and the weighted coefficient of determination.

Statistical analysis.

Statistical comparison of the Δlog₁₀ CFU/ml values was performed by using the Wilcoxon rank sum test for matched regimens in the in vitro and animal models based on the %T>MICs. The mean Δlog₁₀ CFU/ml was used when more than one value existed at a specific %T>MIC (i.e., more than one in vitro model had a given %T>MIC). In vitro model regimens were considered to be matched to the animal model regimens when the difference in %T>MICs between the in vitro and animal models was ≤2%. The %T>MICs for the in vitro models were exactly the same as those for the animal model for 8 of the 15 regimens and within 2% of those for the animal model for the 7 remaining regimens. The statistical analysis was performed with StatView software (version 4.51; Abacus Concepts, Inc., Berkeley, Calif.). A P value of ≤0.05 was considered to be statistically significant.

RESULTS

Preliminary studies. (i) Concentration-time profile.

The ticarcillin concentration-time profiles verified that the target peak concentrations could accurately be achieved in the in vitro model. In addition, AUCs and half-lives ranging from 15 to 30 min that matched the results of counterpart regimens for the animal model were also achieved. Of the five models assessed for penetration into the peripheral compartment at doses ranging from 25 to 50 mg every 2 h, penetration after the 12th dose was as follows: mean, 94%; median, 81%; range, 75 to 146%.

(ii) Growth control studies.

The time to logarithmic growth was determined to be approximately 2 h, suggesting normal growth during the actual experiments in the in vitro model.

Comparison of in vitro and animal models.

The modal MIC of ticarcillin for P. aeruginosa ATCC 27853, as determined in our laboratory, was 16 μg/ml, whereas the MIC reported for the same organism at the time the animal study was performed was 8 μg/ml. The NCCLS acceptable quality control limit of the MIC of ticarcillin for P. aeruginosa ATCC 27853 is 8 to 32 μg/ml (14). Thus, MICs of 16 and 8 μg/ml were used in the in vitro and animal models, respectively, for pharmacodynamic calculations.

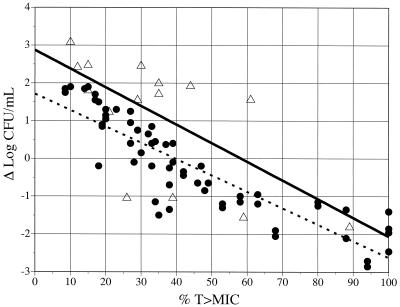
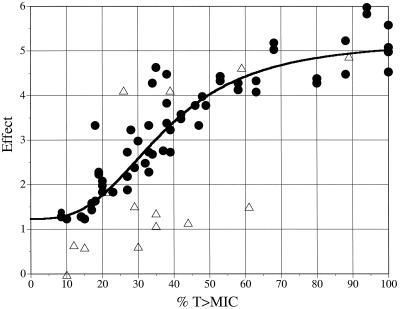
Linear-regression analyses of the relationships between the %T>MICs in the central compartment in the in vitro model or in serum in the animal model and the Δlog₁₀ CFU/ml values yielded reasonable fits (r² = 0.43 and 0.81, respectively) with similar slopes, namely, −0.0493 and −0.0446, respectively (Fig. 2). In general, a greater extent of killing was observed in the animal model than in the in vitro model (the y intercepts were 2.88 log₁₀ and 1.85 log₁₀ for the in vitro and animal models, respectively). The mean Δlog₁₀ CFU/ml in the in vitro model was greater (by 0.86 log₁₀) than that reported for the animal model at a corresponding %T>MIC. Although the in vitro model was associated with a greater Δlog₁₀ CFU/ml, no statistically significant differences were noted between the in vitro and animal models in the Δlog₁₀ CFU/ml values for matched regimens based on %T>MICs for the central compartment (P = 0.087). The relationship between the %T>MIC and effect in the animal model was well characterized by using a sigmoidal Emax model (r² = 0.91). This relationship revealed an effect that was maximized at approximately 60 to 80% of the %T>MIC (Fig. 3).

FIG. 2.

Comparison of in vitro pharmacodynamic and animal models by assessing the relationships between Δlog₁₀ CFU/ml values and %T>MICs over 24 h. Shown are animal model data (•) (r² = 0.81) and in vitro pharmacodynamic model data (▵) (r² = 0.43) as fitted by linear regression.

FIG. 3.

Relationship between %T>MICs (central compartments) and antibacterial effect in animal (•) (r² = 0.91) and in vitro pharmacodynamic (▵) models as fitted to a sigmoidal Emax model.

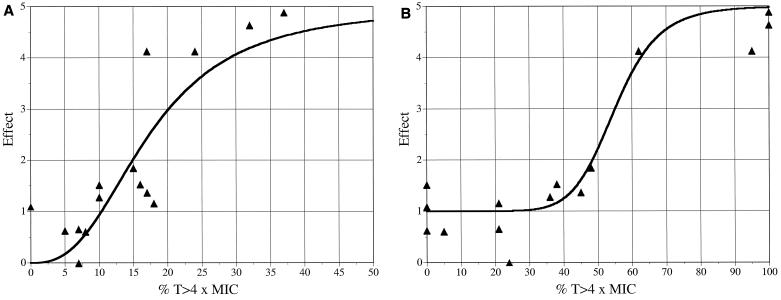
The relationship of the %T>4×MIC to the Δlog₁₀ CFU/ml in the central or peripheral compartment of the in vitro model was a better predictor of outcome than the %T>MIC according to linear-regression analysis (r² = 0.74 versus 0.43 for the central compartment and r² = 0.81 versus 0.28 for the peripheral compartment) (data not shown). With the in vitro model, the relationship between the %T>4×MIC and effect in the central compartment showed a maximizing of effect at approximately 35 to 40% of the %T>4×MIC when the values were fitted with an Emax model (Fig. 4A), although the relationship shown by the Emax model was not improved compared to that shown by linear-regression analysis of %T>4×MIC relative to Δlog₁₀ CFU/ml values (r² = 0.71 versus 0.74). The relationship between the %T>4×MICs and effect in the peripheral compartment of the in vitro model according to a sigmoidal Emax model (Fig. 4B) was better than that of the relationship shown by linear-regression analysis of %T>4×MICs and Δlog₁₀ CFU/ml values (r² = 0.94 versus 0.81) and revealed a maximizing of effect at approximately 70 to 80% of %T>4×MICs. Overall, the best fit of the in vitro model data was shown by analysis of %T>4×MICs and effects in the peripheral compartment with an Emax model (r² = 0.94).

FIG. 4.

Relationship between antibacterial effect and %T>4×MICs in the central (r² = 0.71) (A) and peripheral (r² = 0.94) (B) compartments of the in vitro pharmacodynamic model, as fitted to a sigmoidal Emax model.

DISCUSSION

Pharmacokinetics describes the time course of drug concentrations in relation to the dose or dosage regimen, while pharmacodynamics describes the resulting concentration-effect relationship. A combination of the two allows a description of a drug's effect over time. Such knowledge should be the basis for the design of drug dosing regimens for humans. These relationships have been explored with respect to antibiotics, and it is presently known that β-lactam antibiotics are time-dependent killers and that drugs that inhibit protein or nucleic acid synthesis (e.g., aminoglycosides) are concentration dependent in their antibacterial action (11, 21). Elucidation of these principles has led to the current interest and the growing practices of administering β-lactams by constant infusion (3) and administering aminoglycosides once daily (8, 13, 15).

To date, most published pharmacokinetic-pharmacodynamic information has been generated for animals. A neutropenic-mouse thigh or lung infection model has been extensively utilized, and the resultant publications are considered classic works in this area (11, 12, 21). The validity (with regard to human infection) of such work has been demonstrated, to a limited extent, in clinical studies (16, 17). In the neutropenic-mouse infection model, antibiotic effect has been determined from the changes in the numbers of bacteria in infected tissue (reduction in CFU with antibiotic treatment) or from rates of survival after administration of a protective dose. Optimal dosage regimen principles have been characterized by fitting such data to the sigmoidal dose-effect (Emax) mathematical model (11). Further, major dosage properties or pharmacokinetic-pharmacodynamic characteristics (e.g., the %T>MIC for the infecting organism) which relate to maximum antibacterial action have been identified by correlating them to effect through univariate analysis and stepwise multivariate linear-regression analysis. To generate the necessary data for such an analysis, examination of many different antibiotic doses and dosage regimens for the animal model was necessary. Additionally, a number of antibiotics from a given class were examined for each test organism. Thus, many animals were used. Even so, each dosage group was comprised of only three to five animals. In addition to the often-publicized opposition to animal experimentation in general, the obvious shortcoming of animal models is that mice and other animal species exhibit antibiotic pharmacokinetics very different from that exhibited by humans.

It has long been viewed as desirable to devise an in vitro model in which antibiotic pharmacokinetics, pharmacodynamics, and antibacterial efficacy could be elucidated and compared. Such a model not only would negate or reduce the need for related animal experimentation but also could be used to gain insight into likely optimal dosage regimens for antibiotics prior to actual use in humans. In fact, a number of in vitro models have been described over the years (1, 9). Shortcomings with early versions led to the development of multicompartmental models in which the bacteria were confined to a secondary compartment, which was separated from the central compartment by a dialysis or filter membrane. To draw an analogy to the human body, the secondary compartment is often referred to as the peripheral compartment (in pharmacokinetic terms), and it is suggested that this compartment represents tissue or tissue water space and that the central compartment represents the intravascular space. The surface area-to-volume ratio characterizing the peripheral compartment is crucial to the nature of drug pharmacokinetics in the system, as the passage of drugs across the membrane will follow Fick's law of simple diffusion. This ratio will obviously vary widely in the human body, depending on which tissue or organ is being considered. The surface area-to-volume ratio is particularly important in these models. Although the eventual equilibrium between the drug concentrations in the central and peripheral compartments is usually unaffected by varying ratios, the time to reach equilibrium is affected. Similarly, the disparity between the observed peak and trough concentrations associated with intermittent dosing of antibiotic into the system also varies with the surface area-to-volume ratio.

We have developed an alternative in vitro pharmacodynamic model which incorporates the obvious advantages of the two-compartment system and at the same time addresses what may be shortcomings of other such models. The virtues of this model include the fact that it is composed entirely of easily obtainable laboratory supplies, all of which are either supplied in sterile form or can be autoclaved. Since all connections are Luer-Lok or other quick-connect fittings, the model is easy to assemble and disassemble, provides a closed system, and is not prone to contamination. Importantly, the effective surface area-to-volume ratio is 5.34 cm⁻¹, which is similar to that achieved in studies of skin blisters induced for the purpose of assessing the tissue penetration of antibiotics (2, 18, 19).

The results of the present study strongly suggest that antibiotic pharmacodynamic studies performed with an in vitro model may well produce similar results leading to the same conclusions. Given the theoretical differences between an in vitro system and an animal model, our results demonstrate that there was good agreement between the two models in terms of the relationship between antibiotic effect and the %T>MICs. However, we identified differences in outcomes between the two models, such as a greater degree of variability and less antibacterial effect in the in vitro model than in the animal model (Fig. 2 and 3). Although we are unable to completely explain these findings, they may relate to inherent differences between the in vitro and animal models. The lower degree of antibiotic effect detected in the in vitro model may be explained by the higher growth rate of P. aeruginosa in Mueller-Hinton broth than in neutropenic- and nonneutropenic-mouse thigh models (6, 7). On the average, the Δlog₁₀ CFU for 12 h of growth was approximately 1.7-fold and 5.6-fold greater in the in vitro model than in a neutropenic- and nonneutropenic-mouse thigh model, respectively. The faster growth rate in Mueller-Hinton broth may contribute to greater colony counts at 24 h and thus a different Δlog₁₀ CFU/ml, even if similar degrees of bacterial killing resulted initially. The greater degree of variability in the in vitro model may be explained by the higher growth rate of P. aeruginosa in the in vitro model as well as different %T>MICs in the central and peripheral compartments. Preliminary studies demonstrated that the penetration of ticarcillin into the peripheral compartment was greater than 100% for some dosage regimens. This level of penetration accounts for the large degree of killing in models with relatively low %T>MICs in the central compartment and may explain the stronger relationship between the %T>MIC and the Δlog₁₀ CFU/ml in the peripheral compartment.

The finding that the %T>4×MIC in the central compartment of the in vitro model was a stronger predictor of effect than the %T>MIC is similar to previous findings of other researchers. Jaffe et al. (10) found that the best predictor of cure in subjects with Neisseria gonorrhoeae urethritis was the %T>4×MIC in serum. A possible explanation for the observation that the %T>4×MIC appears to be a better predictor of outcome than the %T>MIC may be that the activities of β-lactams are concentration dependent up to approximately four times the MIC. This finding is consistent with other work suggesting that the antibacterial effect of β-lactam antibiotics is maximized at three to four times the MIC (4, 5, 20).

It would be premature to suggest that such pharmacodynamic studies can henceforth be conducted by using in vitro systems instead of animal infection models. Certainly, other antibiotics and other organisms must be investigated before results such as ours could be extrapolated widely. For example, antibiotics with significant postantibiotic effects may well be associated with different results. Further, the ideal design for such studies may be to conduct animal and in vitro studies in parallel to ensure the consistency of test conditions. Nonetheless, we find our results encouraging and advocate similar comparative work to establish the role of in vitro pharmacodynamic models in antibiotic evaluation and dosage design.