Comparison of Tests for Association and Linkage in Incomplete Families

Abstract

To analyze incomplete families, the following statistical tests can be used: LRAT—a simple likelihood-based association test, TRANSMIT, SIBASSOC/STDT, and RCTDT. We compared these four tests, for the diallelic case, on simulated data sets. The comparisons focused on the power to detect linkage and association when different familial structures, resistance to population stratification, resistance to misclassification of the disease status of the healthy sib, and the effect of nonpaternity were considered. The simulations lead to the following conclusions. The type I errors of TRANSMIT, SIBASSOC/STDT, and RCTDT were not affected by population stratification. LRAT showed bias under strong population stratification. High nonpaternity rates can lead to inflated type I errors, highlighting the importance of identification of half sibs. Under different homogenous models, the power of TRANSMIT was very similar to that of LRAT, and, similarly, no difference in power was observed between SIBASSOC/STDT and RCTDT. Under various recessive and additive models, TRANSMIT was slightly more powerful than SIBASSOC/STDT when monoparental families with one affected and one unaffected sib were analyzed. Under various dominant models, SIBASSOC/STDT was slightly more powerful than TRANSMIT. Misclassification of the disease status of healthy sibs, as well as the discarding of incomplete families, resulted in a consistent loss of power.

Introduction

Family-based studies of genetic association and linkage have been attracting much attention recently. Among these tests, the transmission/disequilibrium test (TDT) (Spielman et al. 1993) is the most widely used. The considerable advantage of family-based tests compared with the classical case-control studies of unrelated individuals is that family-based studies overcome the problem of population stratification (Ewens and Spielman 1995) by using a “constructed sib,” made from the nontransmitted parental alleles, as a control. Family-based tests have been known to be powerful in the detection of association and linkage under different disease assumptions. In addition to these advantages, the TDT is also a very simple and intuitively appealing test. Different family-based tests that test for both linkage and association are available for the diallelic and the multiallelic cases (Self et al. 1991; Knapp et al. 1993; Schaid and Sommer 1994; Sham and Curtis 1995a; Schaid 1996; Spielman and Ewens 1996; Morris et al. 1997b). Their respective advantages usually depend on the disease model. Since all these tests are conditional on the parental genotypes, the genotypes of both parents must be known.

However, in many situations the parental genotypes may not be available. In adult-onset diseases, the parents of the affected individual may already have died, or samples may be unavailable for a variety of other reasons, leading to a reduction in the number of fully informative trios available. In this situation, it is tempting to try to reconstruct the genotype of the missing parent, and this can be done in certain cases. But, as Sham and Curtis (1995b) pointed out, this approach introduces bias and should not be used in the diallelic case. Omitting incomplete families from the statistical analysis discards information that could be useful and that could increase the power of the test. To overcome the problem of bias, there are currently two main approaches. The first is one is to estimate the genotype of the missing parent by using the estimated allelic or genotypic frequencies; we shall refer to this approach as “vertical tests.” The second approach is to rely on the use of healthy sibs as internal controls; we shall refer to this approach as “horizontal tests.” A combination of both approaches can also be used and has been introduced by Knapp (1999).

We will present a new test, named the “likelihood-ratio association test” (LRAT), and compare it with some of the tests recently developed to analyze incomplete families, by which we mean families with at least one affected child available and one parent missing. Using simulated families, we address the question of how the different tests perform under population stratification, nonpaternity, and misclassification of the healthy sib. We report type I errors under the null hypothesis of no association and measure the power for varying levels of disequilibrium, using different disease models and different family structures. These analyses reveal a marked effect on power, introduced by misclassification of disease status and the strategy of discarding incomplete families. We also observe a bias resulting from high nonpaternity levels.

Methods

Reconstruction of the Missing Parent—Vertical Tests

To our knowledge, the first program to use the approach of reconstructing the missing parental genotype to test for association in incomplete families is TRANSMIT (Clayton 1999). It is a generalization of the TDT and uses the EM algorithm to estimate the missing information. The test statistic reduces to that of the TDT when families are full trios and markers are diallelic. A similar generalized score test was introduced by Schaid and Li (1997), but the program was not available for use in this analysis.

LRAT is a classical likelihood-ratio test in which assumptions are made about population structure. The probability that allele 1 will be transmitted from a heterozygous parent to an affected child is parameterized as “a”; the null hypothesis tested is a=.5; and the frequency of allele 1 is denoted by “p” and is treated as a nuisance parameter. Since we are considering the diallelic case, the frequency of allele 2 is (1-p). Maximization of the likelihood is then performed over the values of a and p, each numerically on a grid with spacing .001. When the families come from different ethnic groups or populations, a different estimate of p can be used for each group. Since the probability for each type of incomplete family is calculated, the bias identified by Sham and Curtis (1995b) is overcome. When estimating the genotypic frequencies, we assume that the whole population is in Hardy-Weinberg equilibrium and that the missing parent is missing at random—that is, the transmitted allele does not influence the absence of the parents. Details of the calculations can be found in Appendix A.

The use of a likelihood-ratio test to test for association in the presence of linkage in complete families is one of the possible family-based tests and seems to be powerful (Morris et al. 1997a; Sham 1998). Subsequent to the initial submission of this report, a similar approach—applied to genotypes, rather than to alleles—was reported by Weinberg (1999).

Working with Healthy Sibs—Horizontal Tests

Curtis (1997) has presented a sib association test. The data requirements are (a) that there be at least one affected and one unaffected sibling per family and (b) that the members of the same families should not all have the same genotypes. SIBASSOC is available from the Web, in both a DOS version and a UNIX version, and is well documented. The pairwise test involves random selection of one affected sib per family and, as a control, the sibling who has the genotype most different from that of this affected sib.

Spielman and Ewens (1998) have presented the sib transmission/disequilibrium test (STDT); the program is also available from the Web. The data requirements are the same as those for SIBASSOC—that is, at least one affected and one unaffected child per family, who have different genotypes. The test statistic is obtained by comparing the genotypes of affected children versus the genotypes of the unaffected children within families. Unlike in SIBASSOC, the number of affected and unaffected children per family are taken into account, along with genotypic information on all the sibs.

Also, Boehnke and Langefeld (1998) have presented different tests, based on discordant-sib-pair (DSP) methods. Monks et al. (1998) have shown that the three tests—SIBASSOC, STDT, and DSP—are equivalent for diallelic markers. In our simulations, we used the program SIBASSOC, which was obtained from the D. Curtis Web site, since the UNIX version was easily implemented in our program.

Horvath and Laird (1998) have presented a sign test, the SDT, that compares the average number of alleles in affected versus unaffected sibs. For the situation in which we are interested—that is, a diallelic marker and a single affected and a single unaffected sib per family—they showed both that, for testing for linkage, the SIBASSOC/STDT is more powerful than the SDT but that, for testing for association, neither test is uniformly more powerful.

Combining the Two Approaches

Knapp (1999) has developed a program called the “reconstruction combined TDT” (RCTDT), which combines the two approaches. This program reconstructs the missing parental genotypes when these can be reconstructed, with certainty, from the sibs. On the other hand, when the missing parental genotype cannot be deduced, the STDT is calculated and included in the test statistic. Since this approach is different from the others, we have written a FORTRAN program for the purpose of the present report. The potential bias in the reconstruction of the missing genotypes is overcome by conditioning the probabilities on the fact that one is able to reconstruct the missing information. The following four programs were therefore selected for comparison: TRANSMIT, LRAT, SIBASSOC, and RCTDT. Note that we are testing for both linkage and association, since, because there is only one affected sib per family, these tests are valid tests of association.

Simulation Study

When data sets are simulated, it may be difficult to decide on the simulation parameters to use. The disease model and the frequency of the disease allele have to be chosen. Since our original interest was in tuberculosis and in diallelic candidate genes with a single common allele and a mutant disease allele, we have selected the following models, which are reasonably close to our interests and should cover a variety of situations. Nonpaternity rates were varied from 10% to 40%. Meisner (1999) has reported an estimated overall nonpaternity rate of ∼15.3% in the southern Indian population and also mentions observed rates of 32% in families from Vishakapatnam. In Africa, Ruwende (1996) found ∼30% nonpaternity in some families. The values presented are all based on 1,000 replicates of 100 families. The pedigrees were simulated by the program SLINK (Ott 1989; Weeks et al. 1990).

The models represented in table 1 were simulated in the absence of association between the marker and the disease allele, in families sampled from a homogeneous population. The following notation was adopted to clarify the models used: the first letter refers to the population (“H” = homogeneous), followed by p, the disease penetrances, and the frequency of the disease allele. Note that the disease parameters are not relevant here, since the disease is not associated with the marker. For the null hypothesis of random transmission in families sampled from two populations with different allelic frequencies, see table 2; for the null hypothesis of random transmission in families sampled from a homogeneous population with different nonpaternity rates, see table 3.

Table 1.

Specification of Homogeneous Models Used in Simulations

Model (p)	Disease Penetrance	Disease-Allele Frequency(%)
H10D5 (10%)	Fully dominant	5
H10R5 (10%)	Fully recessive	5
H10A5 (10%)	Additive	5
H25D10 (25%)	Fully dominant	10
H25R10 (25%)	Fully recessive	10
H25A10 (25%)	Additive	10
H50D15 (50%)	Fully dominant	15
H50R15 (50%)	Fully recessive	15
H50A15 (50%)	Additive	15

Table 2.

Specification of Stratified Models Used in Simulations

Model	Specification
S510a	25 Families with p=5%, 75 families with p=10%
S1025a	25 Families with p=10%, 75 families with p=25%
S2550a	25 Families with p=25%, 75 families with p=50%
S510b	50 Families with p=5%, 50 families with p=10%
S1025b	50 Families with p=10%, 50 families with p=25%
S2550b	50 Families with p=25%, 50 families with p=50%
S510c	80 Families with p=5%, 20 families with p=10%
S1025c	80 Families with p=10%, 20 families with p=25%
S2550c	80 families with p=25%, 20 families with p=50%

Table 3.

Specification of Nonpaternity Models Used in Simulations

Model	p	Nonpaternity Rate(%)
H10NP10	10%	10
H10NP20	10%	20
H10NP40	10%	40
H25NP10	25%	10
H25NP20	25%	20
H25NP40	25%	40
H50NP10	50%	10
H50NP20	50%	20
H50NP40	50%	40

For the power comparison between the four test statistics, we used a diallelic marker that was close enough to the disease gene that no recombination was assumed, as has been done elsewhere (Boehnke and Langefeld 1998). Existing association between the candidate gene and the disease locus was modeled, by use of the respective haplotypic frequencies, as a function of the linkage-disequilibrium parameter e_D1=[freq(D×A1)/freq(D)×freq(A1)], where D denotes the disease allele and A1 denotes the associated marker allele, as has been done elsewhere (Morris et al. 1997b). To estimate the effect of misclassification of the healthy sib, the second sib was simulated as affected in 10% of the cases and in 25% of the cases, and its disease status was changed to healthy. To estimate the effect of discarding the incomplete families, we compared the power of the TDT in families with both parents versus the power of TRANSMIT when the families with only one parent were retained. We simulated 100 families, of which either 0, 25, or 50 had only a single parent and an extra unaffected sib. Twelve different disease models were used, and the linkage-disequilibrium parameter e_D1 varied from 1.2 to 2.0. The model parameters are given in table 4, and the respective haplotypic frequencies are given in Appendix B. The penetrances for the additive disease model were .6 for the homozygous disease genotype, .3 for the heterozygous genotype, and 0 for noncarriers of the disease allele; the penetrances for the multiplicative disease model were .2 for the homozygous disease genotype, .04 for the heterozygous genotype, and 0 for noncarriers of the disease allele.

Table 4.

Specification of Disease Models Used in Simulations

Model	p	Disease Penetrance	Disease-Allele Frequency(%)
E10D5	10%	Fully dominant	5
E10R5	10%	Fully recessive	5
E10A5	10%	Additive	5
E10M5	10%	Multiplicative	5
E25D10	25%	Fully dominant	10
E25R10	25%	Fully recessive	10
E25A10	25%	Additive	10
E25M10	25%	Multiplicative	10
E50D15	50%	Fully dominant	15
E50R15	50%	Fully recessive	15
E50A15	50%	Additive	15
E50M15	50%	Multiplicative	15

Results

Single Parent and Single Affected Child

First we analyzed the accuracy of the null distribution under the hypothesis of no association between the candidate gene or marker and the disease, for nine homogeneous models. We have reported the type I errors in table 5. The power of the two selected tests—LRAT and TRANSMIT—was simulated as a function of the linkage-disequilibrium parameter. We varied this parameter between 1.2 (i.e., almost no association) and 2.0 (i.e., strong association). The simulated power at 5% corresponds to the percentage of times that the test statistic was higher than the theoretical value for a χ², with 1 df, at the 5% level, which is 3.84.

Table 5.

Type I Error: Level of Significance for 3.84, Which Corresponds to the 5% Level^[Note]

	Type I Error
Population	TRANSMIT	LRAT	SIBASSOC
Homogeneous:
H10D5	6.7	5.3	5.3
H10R5	3.2	5.8	5.2
H10A5	4.7	6.1	5.2
H25D10	3.3	4.2	4.3
H25R10	4.9	5.9	5.4
H25A10	5.1	4.5	6.1
H50D15	4.3	5.6	4.2
H50R15	4.4	5.3	4.1
H50A15	4.6	6.1	5.4
Stratified:
S510a	4.5	6.5	4.1
S1025a	4.8	3.9	5.7
S2550a	5.5	4.7	6.3
S510b	4.2	10.0	5.4
S1025b	4.8	6.9	4.9
S2550b	5.8	7.6	5.5
S510c	3.3	6.6	5.4
S1025c	4.9	4.1	6.6
S2550c	4.0	5.1	5.4
Nonpaternity:
H10NP10	6.0	NA	5.0
H10NP20	7.3	NA	4.3
H10NP40	11.9	NA	7.7
H25NP10	6.5	NA	5.5
H25NP20	7.6	NA	6.2
H25NP40	10.4	NA	7.0
H50NP10	6.2	NA	4.7
H50NP20	6.6	NA	6.2
H50NP40	7.9	NA	6.7

Note.— The parameters for each model are described in tables 1–3. The simulated interval for 1,000 replicates is (.037, .063).

The tests LRAT and TRANSMIT match well the theoretical χ² distribution under the hypothesis of no association between the disease and the marker, in a homogeneous population. In our simulations, LRAT and TRANSMIT returned the same values, up to two decimal places, in homogeneous populations. For a population sampled from two populations with different allelic frequencies, LRAT had high levels of type I error and, therefore, is not valid. This is particularly evident for models “b” (see tables 2 and 5)—that is, when half the sampled families are from one population and the other half are from another population. TRANSMIT seemed to be resistant to population stratification, in all the models that we used.

In families with only one parent and one affected sib, the powers of LRAT and TRANSMIT were compared. As can be seen in tables 6 and 7, LRAT and TRANSMIT have, for the nine different models, similar power to detect association in the pedigrees, independently of the strength of the disequilibrium or the disease model.

Table 6.

Power Simulations Based on 1,000 Replicates of 100 Nuclear Families Including One Parent and One Affected Offspring

	Power
Model	LRAT	TRANSMIT
Dominant:
E10D5:
1.2	.062	.050
1.4	.083	.063
1.6	.097	.082
1.8	.168	.144
2.0	.216	.183
E25D10:
1.2	.074	.070
1.4	.126	.110
1.6	.199	.183
1.8	.325	.313
2.0	.454	.441
E50D15:
1.2	.105	.102
1.4	.256	.254
1.6	.515	.515
1.8	.783	.786
2.0	.922	.923
Recessive:
E10R5:
1.2	.108	.090
1.4	.142	.124
1.6	.272	.245
1.8	.447	.397
2.0	.598	.557
E25R10:
1.2	.121	.114
1.4	.400	.386
1.6	.627	.620
1.8	.868	.866
2.0	.970	.967
E50R15:
1.2	.338	.337
1.4	.871	.873
1.6	.998	.998
1.8	1.000	1.000
2.0	1.000	1.000

Table 7.

Power Simulations Based on 1,000 Replicates of 100 Nuclear Families Including One Parent and One Affected Offspring

	Power
Model	LRAT	TRANSMIT
Additive:
E10A5:
1.2	.049	.045
1.4	.063	.056
1.6	.121	.104
1.8	.156	.134
2.0	.217	.191
E25A10:
1.2	.071	.066
1.4	.126	.114
1.6	.240	.222
1.8	.354	.341
2.0	.537	.519
E50A15:
1.2	.118	.118
1.4	.307	.306
1.6	.587	.589
1.8	.855	.859
2.0	.960	.962
Multiplicative:
E10M5:
1.2	.047	.039
1.4	.075	.058
1.6	.125	.103
1.8	.161	.141
2.0	.213	.186
E25M10:
1.2	.058	.054
1.4	.172	.152
1.6	.292	.272
1.8	.434	.416
2.0	.614	.592
E50M15:
1.2	.137	.139
1.4	.418	.416
1.6	.759	.757
1.8	.963	.962
2.0	.999	.999

One Affected and One Unaffected Sib

The accuracy of the null distribution was simulated as before, to compare the three test statistics—TRANSMIT, RCTDT, and SIBASSOC/STDT. Nine models were simulated with a homogeneous population. We did not detect, in the results from RCTDT and SIBASSOC, any difference >1%. The type I errors for SIBASSOC are reported in table 5. The correct level of significance was achieved for both homogeneous and stratified populations. Three models with three different rates of nonpaternity were simulated with a homogeneous population. We observed an increase in the type I error in all three tests, even at rates that are likely to be found in real populations (nonpaternity rate 25%). TRANSMIT was more sensitive to nonpaternity rates than was SIBASSOC. When TRANSMIT identifies inconsistent transmissions, it will automatically exclude those families from the analysis. If the nonbiological parent is heterozygous, it will never be identified as an inconsistent transmission. Only situations in which the nonbiological parent is homozygous and the sib is from a different homozygosity will result in exclusion of that family from the analysis. As a result, there will be an overrepresentation of heterozygous fathers in the families, increasing the number of informative transmissions. A bias similar to that originally identified by Sham and Curtis (1995b) will be the result of nonpaternities. The slight increase in the type I error of SIBASSOC was observed only when nonpaternity rates were high and the associated allele was rare, possibly because (a) the number of homozygous mutants is very rare and (b) asymptotic results might not be applicable.

The power to detect association was simulated in a homogeneous population, with TRANSMIT and SIBASSOC. As can be seen in figure 1, inclusion of an extra healthy sib increases the power of TRANSMIT, compared with what is seen with nuclear families of two individuals (tables 6 and 7). TRANSMIT was more powerful than SIBASSOC, under the recessive, additive, and, especially, multiplicative models: E10R5, E10A5, E25A10, E50R15, E50A15, E10M5, E25M10, and E50M15 (R = recessive, A = additive, and M = multiplicative). Under the multiplicative disease models E25M10 and E50M15 and for a linkage-disequilibrium parameter of 1.4, TRANSMIT had almost twice the power of SIBASSOC (fig. 1B). Under the dominant models, SIBASSOC had more power than TRANSMIT, especially under models E10D5 and E25D10 (D = dominant). The two tests seemed to achieve similar power under model E25R10. We did not observe any detectable difference between the values for the STDT and those for the RCTDT, in the diallelic case.

Figure 1.

Power simulations based on 1,000 replicates of 100 nuclear families including one parent, one affected sib, and one unaffected sib. The different lines represent comparisons of SIBASSOC versus TRANSMIT, under various fully dominant (top left), additive (top right), fully recessive (bottom left), and multiplicative (bottom right) models.

Misclassification reduced the power of all the statistical tests. Figure 2 presents the power when SIBASSOC and TRANSMIT were used to analyze families with one parent, one affected sib, and one healthy sib. The level of misclassification corresponds to the percentage of healthy sibs who were erroneously categorized as healthy instead of affected. There is considerable decrease in the power of both TRANSMIT and SIBASSOC. Similar results were obtained under recessive and additive models (data not shown).

Figure 2.

Power comparison under various homogenous dominant models and percentages (0%, 10%, and 25%) of misclassification of unaffected sib, for SIBASSOC (top) and TRANSMIT (bottom).

When the strategy of analyzing all the available families is compared with that of discarding families that include only one parent, it is clear that the latter is the poorer strategy. When an extra healthy sib is available, the power of TRANSMIT is not much reduced, compared with the power when the original classic trio is used (figs. 3–6), even if half of the families include only a single parent. On the other hand, performing a TDT on only 75 or 50 families considerably reduces the power to detect association. Whichever test—SIBASSOC/STDT or TRANSMIT—is used to analyze the families, the TDT performed on 50 families always had the lowest power.

Figure 3.

Power comparison of the TDT, for different familial structures, on the basis of dominant models E10D5 (top), E25D10 (middle), and E50D15 (bottom).

Figure 4.

Power comparison of the TDT, for different familial structures, on the basis of recessive models E10R5 (top), E25R10 (middle), and E50R15 (bottom).

Figure 5.

Power comparison of the TDT, for different familial structures, on the basis of additive models E10A5 (top), E25A10 (middle), and E50A15 (bottom).

Figure 6.

Power comparison of TDT, for different familial structures, on the basis of multiplicative models E10M5 (top), E25M10 (middle), and E50M15 (bottom).

Discussion

Four tests that allow analysis of incomplete families—that is, families with at least one missing parent—have been compared. LRAT and TRANSMIT are “vertical” tests, which try to reconstruct the missing parent; SIBASSOC and STDT are “horizontal” tests, which compare affected and unaffected siblings inside families; and RCTDT combines both approaches.

When one parent and one affected sib are available in each family, TRANSMIT and LRAT can be used to perform the analysis. When one affected and one healthy sib are available per family, TRANSMIT, SIBASSOC, and RCTDT can be compared.

We have observed in simulated families that stratification is only a problem when LRAT is used. LRAT uses only one parameter to estimate the allelic frequency, and this is particularly inefficient when the population is a mixture of two populations with very different frequencies; in real data sets, different ethnic groups might not have such different frequencies. To overcome this problem of population stratification, it is possible to take into account the ethnic group and to use different allelic frequencies and different transmission parameters for the different ethnic groups. This increases the degrees of freedom, as more parameters are used, but overcomes the problem of population stratification. Clearly, this requires accurate knowledge of the individual's ethnic group. TRANSMIT did not appear to suffer from population stratification, even under extreme situations, and thus we recommend that TRANSMIT be used. Families that include only one parent and one affected offspring carry information that does increase the power to detect association, and they therefore should be included in the analysis. Including an extra sib in the families increases the power of TRANSMIT, since it allows the missing parental genotype to be reconstructed more precisely. Discarding incomplete families results in loss of information and power to detect association; we therefore recommend that incomplete families be included in the analysis.

TRANSMIT, SIBASSOC, and RCTDT vary slightly in power, depending on the disease model used. The biggest difference in power was observed under the multiplicative models, where TRANSMIT outperformed the other tests. It is not surprising that TRANSMIT is the most powerful test under multiplicative disease models, since, like the TDT test, it assumes a multiplicative disease model. Misclassification of the disease status of the healthy sib reduces the power to detect association. Nonpaternity did not decrease power but, instead, actually increased power (data not shown), as a result of inflated type I errors: the null distribution was no longer accurate, even for a homogeneous population with relatively high (25%) nonpaternity rates. This important result illustrates the importance of typing the multiallelic markers or multiple diallelic markers, to identify, with certainty, any families with half sibs and to exclude them from the analysis.

Clearly, the choice of which test to use is going to be a decisive factor in the structure of the data. The RCTDT is a very appealing approach, since it combines both vertical and horizontal approaches and, in larger families, performs better than the STDT (Knapp 1999). Since most putatively functional candidate gene polymorphisms are diallelic, our simulations and discussions have concentrated on the diallelic case only. For multiallelic markers such as microsatellite markers, the conclusions might be different. The multiallelic case can be reduced to the diallelic case by merging of the alleles, as has been discussed by Boehnke and Langefeld (1998). A comparative study of sibship tests, by Monks et al. (1998), has discussed the multiallelic case. The current analyses have highlighted the fact that both misclassification of disease status and nonpaternity may be more problematic than population stratification and, therefore, that vertical tests based only on affected sibs will, under certain conditions, be more powerful than horizontal tests.

Appendix A: Transmission Probabilities

Transmission probabilities can be parameterized as functions of a and p only if all the sibs are affected. Table A1 shows the probability that the different types of families will be observed, when there is or is not a missing parent.

Table A1.

^[Note]

Parental Genotype(s)	Affected Child’s Genotype	Probability
11,11	11	p4
11,12	11	4p3qa
11,12	12	4p3(1-a)
11,22	12	2p2q2
12,12	11	(2pq)2a2
12,12	12	2(2pq)2a(1-a)
12,12	22	(2pq)2(1-a)2
22,12	12	4pq3a
22,12	22	4pq3(1-a)
22,22	22	q4
11	11	p4+2p3qa
11	12	2p3q(1-a)+p2q2
12	11	2p3qa+4p2q2a2
12	12	2p3q(1-a)+8p2q2a(1-a)+2pq3a
12	22	4p2q2(1-a)2+2pq3(1-a)
22	12	p2q2+2pq3a
22	22	2pq3(1-a)+q4

Note.— The likelihood is Σ_{family type}N_{family type}×log(P_{family type}), where “family type” denotes the different types of family genotypes shown in table A1, N is the number of times that such a family is observed in the data set, and P is the probability that that type of family will be observed. Under the null hypothesis (a=.5), maximize the likelihood over p only; under the hypothesis a≠.5, maximize the likelihood over a and p. The test statistic for LRAT is 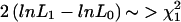. When different populations or ethnic groups are present in the data set, the test is performed on each item separately. The resulting χ² values can then be added together for an overall test.

Appendix B: Frequencies of Allele 1 Disease Haplotype, as a Function of the Linkage-Disequilibrium Parameter

The models shown in table B1 refer to the description in the Simulation Study section.

Table B1.

	Frequency of Allele 1 Disease-Haplotype, for Modela
ED1	E10*5	E25*10	E50*15
1.2	.006	.03	.09
1.4	.007	.035	.105
1.6	.008	.04	.12
1.8	.009	.045	.135
2.0	.01	.05	.15

An asterisk (*) denotes A, D, R, or M.