Data Mining Applied to Linkage Disequilibrium Mapping

Abstract

We introduce a new method for linkage disequilibrium mapping: haplotype pattern mining (HPM). The method, inspired by data mining methods, is based on discovery of recurrent patterns. We define a class of useful haplotype patterns in genetic case-control data and use the algorithm for finding disease-associated haplotypes. The haplotypes are ordered by their strength of association with the phenotype, and all haplotypes exceeding a given threshold level are used for prediction of disease susceptibility–gene location. The method is model-free, in the sense that it does not require (and is unable to utilize) any assumptions about the inheritance model of the disease. The statistical model is nonparametric. The haplotypes are allowed to contain gaps, which improves the method's robustness to mutations and to missing and erroneous data. Experimental studies with simulated microsatellite and SNP data show that the method has good localization power in data sets with large degrees of phenocopies and with lots of missing and erroneous data. The power of HPM is roughly identical for marker maps at a density of 3 single-nucleotide polymorphisms/cM or 1 microsatellite/cM. The capacity to handle high proportions of phenocopies makes the method promising for complex disease mapping. An example of correct disease susceptibility–gene localization with HPM is given with real marker data from families from the United Kingdom affected by type 1 diabetes. The method is extendable to include environmental covariates or phenotype measurements or to find several genes simultaneously.

Introduction

The use of linkage disequilibrium (LD) in detecting disease genes has recently drawn much attention in genetic epidemiology. LD is evaluated with association analysis, which, when applied to disease-gene mapping, requires the comparison of allele or haplotype frequencies between the affected and the control individuals, under the assumption that a reasonable proportion of disease-associated chromosomes has been derived from a common ancestor. Traditional association-analysis methods have long been used to test the involvement of candidate genes in diseases and, in special circumstances, to fine-map disease loci found by linkage methods. The testing has mostly been done using simple two-point measures.

Improved statistical methods to detect LD have been presented lately (Terwilliger 1995; Devlin et al. 1996; Lazzeroni 1998; McPeek and Strahs 1999; Service et al. 1999). The newer methods are based on statistical models of LD around a disease susceptibility (DS) gene. Genomic regions—rather than alleles—that are shared among affected individuals, are searched for. The recombination history from the common ancestor to the present day is taken into account with more or less simplified statistical models. The power of these methods, as well as their ability to localize the correct position of the DS gene, has been shown to be better than that of traditional methods. Some of the models are robust to high levels of etiologic heterogeneity (McPeek and Strahs 1999; Service et al. 1999). However, the methods contain assumptions about the inheritance model of the disease and the structure of the survey population, and the effects of violations of these assumptions in the real data are not known. In addition, they can only consider association of one region at a time. Thus, they are currently best suited for fine mapping, rather than complex disease mapping or genome screening. The methods also tend to be computationally heavy.

In this study, we introduce haplotype pattern mining (HPM), a technique that uses data mining methods in LD-based gene mapping. HPM is based on algorithms developed to find frequent patterns efficiently from large databases (Agrawal et al. 1993, 1996). The method uses haplotypes as input; they can be obtained, for example, with GENEHUNTER (Kruglyak et al. 1996). In diseases with a reasonable genetic contribution, affected individuals are likely to have higher frequencies of associated marker alleles near the DS gene than control individuals. Combinations of marker alleles which are more frequent in disease-associated chromosomes than in control chromosomes, are searched for in the data, without assumptions about the mode of inheritance of the disease. These combinations, haplotype patterns, are sorted by the strength of their association to the disease, and the resulting list of haplotype patterns is used in localizing the DS gene.

The method is an algorithm-based extension of traditional association analysis. It works with a nonparametric statistical model and without any genetic models. The localization power of the method is high, even with weak associations—for example, when disease-associated haplotypes are found in only 5%–10% of disease-associated chromosomes at realistic sample sizes (100–200 affected individuals) with either microsatellite or single-nucleotide polymorphism (SNP) data. The method is robust to mutations as well as to missing and erroneous data. Since HPM can handle high degrees of etiologic heterogeneity, it can be successful in complex disease mapping. We show as an example that HPM can accurately localize a DS gene in marker data from a complex disease, type 1 diabetes. For future work, it is conceptually rather straightforward to extend the approach to find several genes simultaneously.

Methods

LD, the nonrandom association of marker alleles and haplotypes to the disease, is likely to be strongest around the DS gene; consequently the locus is likely to be where most of the strongest associations are. In the HPM method we search for shared, flexible haplotypes that may contain gaps and find out which ones are strongly associated to the disease status. We then use a nonparametric model for predicting the DS locus, on the basis of the locations of the haplotypes. Permutation tests can be used to contrast the results against the null hypothesis that there is no gene effect.

Haplotype Patterns and Disease Association

We examine linkage disequilibrium by looking for haplotype patterns that consist of a set of nearby markers, not necessarily consecutive ones. Given a marker map M with k markers m₁,...,m_k, a “haplotype pattern” P on M is defined as a vector (p₁,...,p_k), where each p_i is either an allele of marker m_i or the “don’t care” symbol (*). The haplotype pattern P occurs in a given haplotype vector (chromosome) H=(h₁,...,h_k) if p_i=h_i or p_i = * for all i,1⩽i⩽k. For example, consider a marker map of 10 markers. The vector P₁ = (*, 2, 5, *, 3, *, *, *, *, *), where 1, 2, 3,… are marker alleles, is an example of a haplotype pattern. This pattern occurs, for instance, in a chromosome with haplotype (4, 2, 5, 1, 3, 2, 6, 4, 5, 3).

Our goal is to search for haplotype patterns that roughly correspond to haplotypes identical by descent in the disease-associated chromosomes. In doing this, there are two major issues with respect to the shapes of haplotype patterns: the genetic length of the significant part of the patterns, and gaps. We define the “(genetic) length” of a haplotype pattern P=(p₁,...,p_k) as the maximum distance, in Morgans, between any two markers m_i,m_j with p_i≠*≠p_j. Searching for haplotype patterns of arbitrary length hardly makes sense; it is unlikely that genetically extremely long patterns will be discovered, at least not in significant numbers. Consequently, when haplotype patterns are searched for, the maximum length of patterns to be considered can be constrained with an optional pattern-search parameter to the HPM method.

We allow for gaps in the haplotype patterns, since mutations, errors, missing data, and recombinations can corrupt continuous haplotypes. Marker mutations and errors typically cause very short gaps only. Missing information can span several consecutive markers, depending on the data collection scheme. Longer gaps can be introduced by double recombinations which, however, are rare on genetically short distances. In the HPM method, the maximum number and maximum length of gaps can be controlled with pattern search parameters.

Mining Disease-Associated Haplotype Patterns

We present the HPM method in terms of the (signed) χ² measure of marker-disease association. A signed version of the measure is used in order to discriminate disease association from control association. The signed χ² measure ± χ²(P) of a haplotype pattern P is positive if P is more frequent in cases than in controls, and negative otherwise. Given a “(positive) association threshold” x, we say that P is “strongly associated” with the disease if ±χ²(P)⩾x.

The first part of the HPM method can be described as follows. Given the data—markers M, haplotypes H, and phenotypes Y—the task is to output all haplotype patterns P that are strongly associated with the disease status for a given value of the association threshold x. We denote the collection of all such haplotype patterns by 𝒫—that is, 𝒫 = {P is a haplotype pattern on M | ± χ²(P)⩾x}. If pattern parameters are specified—a maximum genetic length, a maximum number of gaps, or a maximum length for gaps—the task is refined by requiring that these additional restrictions are also fulfilled.

The first observation in solving the pattern-mining task is that given an association threshold x, a lower bound can be derived for the frequency of strongly associated haplotype patterns (appendix A). On another hand, given such a frequency threshold, all patterns exceeding the threshold can be enumerated efficiently with data-mining algorithms (Agrawal et al. 1993; Agrawal et al. 1996) or a standard depth-first search method. An algorithm that first finds all haplotype patterns whose frequency exceeds the computed lower bound and then evaluates the association measure on them, is guaranteed to find the exact set of strongly disease-associated patterns.

The approach is suitable for finding protective haplotypes, by considering patterns P with ±χ²(P)⩽-x. The derivation of the lower bound for the frequency among controls is identical to the case above. Obviously, both disease-associated and protective haplotypes can be found when |±χ²(P)|⩾x.

Gene Localization

Haplotype patterns close to the DS locus are likely to have stronger association than haplotypes further away; consequently the locus is likely to be where most of the strongest associations are. We compute the marker frequency f(m_i) of marker m_i (with respect to M,H,Y,x) as the number of patterns that contain marker m_i, possibly in a gap: f(m_i)=|{P=(p₁,...,p_k)∈𝒫| there exist t⩽i and u⩾i such that p_t≠*≠p_u}|. The idea is that each haplotype pattern roughly corresponds to a continuous chromosomal region, potentially identical by descent, where gaps allow for corruption of marker data. While markers within gaps are not used in measuring the disease association of the pattern, the whole chromosomal region of the pattern is thought to be relevant.

The marker frequency gives a score for each marker. On the condition that we assume a DS gene to be present; for example, on the basis of linkage analysis, we would predict the gene to be somewhere close to the markers with largest frequencies. As a point prediction 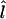, we simply give the locus of the most frequent marker: 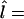locus of marker arg max_i [f(m_i)]. This does not, of course, imply that we assume the DS locus to overlap with the marker in reality; we simply make predictions about the granularity of marker density. Consequently, the optimal point predictions of our method are within one half of the intermarker distance from the true loci.

Permutation Tests

The results obtained by considering marker frequencies can be contrasted against the null hypothesis that all the chromosomes are drawn from the same distribution; that is, there is no gene effect in the disease status. We propose to permute randomly the status fields of the chromosomes, keeping the proportions of affected and control chromosomes constant, in a fashion similar to the methods of Churchill and Doerge (1994), Laitinen et al. (1997), and Long et al. (1998).

We approximate markerwise P values using permutations and then predict the DS gene to be in the vicinity of the marker with the smallest empirical P value. Consecutive markers are dependent, and thus a large number of mutually dependent P values are produced. This is not a problem, since we do not use the P values for hypothesis testing, but only for ranking markers.

Results

Simulated Data Sets

We evaluated the performance of the proposed HPM method with simulated data sets that correspond to a recently founded, relatively isolated founder subpopulation. Simulation of a population isolate was chosen, since it is recommended as the study population for LD studies (Wright et al. 1999). However, the method can be applied to any population that is suitable for LD analysis, since no assumptions are made about the population structure.

An isolated founder population which grows from the initial size of 300 to ∼100,000 individuals in 500 years was simulated. Each individual was assigned to have one pair of homologous chromosomes. The genetic length of the chromosomes was 100 cM for both males and females. No chiasma interference was modeled. In all microsatellite-marker simulations, the information content (PIC) of each marker was fixed at 0.7, and the markers were spaced at intervals of 1 cM. In the SNP data, marker loci were simulated with a density of 3 markers per 1 cM of chromosome. The allele frequency was set to 0.5, and the PIC was thus fixed at 0.375.

We used a dominant disease model with a high phenocopy rate in our experiments. The sample size was 400 chromosomes (200 individuals), of which 200 were control chromosomes. This relatively small sample size was used to study the performance of the method in realistic situations. In the affected sample the proportion of mutation-carrying chromosomes, denoted by A, was either 2.5%, 5%, 7.5%, or 10%, corresponding to overall relative risks of λ=1.2, λ=1.7, λ=2.7, and λ=4.1, respectively, for first-degree relatives (for principles of risk calculations, see studies by Risch [1990], Suarez et al. [1978], and Camp [1997]). These low IBD and λ values were chosen, as the higher are easy to handle with existing methods. We ignored marker mutations in the simulation procedure, but compensated for this by evaluating the performance in presence of missing and corrupted data. Both were introduced by removing or changing alleles randomly and independently. The amount of missing data varied between 0% and 20%, and the fraction of corrupted alleles between 0% and 10%.

We used the Populus simulator package (V. Ollikainen, H. Mannila, R. Kilpikari, M. Koivisto, H. Kärkkäinen, M. Mäkelä, P. Onkamo, S. Smolander, and J. Kere, unpublished data) to obtain artificial data sets for the analyses. The package consists of a pedigree generator and a chromosome simulator, and enables creation of data sets with realistic linkage disequilibrium. A detailed description of population parameters as well as the simulation procedure are presented in appendix B.

Parameters

We performed extensive gene localization experiments with different parameter values. For a basic setting, within which we compared the performance of the method in different data sets, we selected the following parameter values. The maximum length of haplotype patterns was restricted to seven consecutive markers, which corresponds to segments of 6–8 cM. This is close to the average length of shared haplotypes in a population of ∼500 years of age. To allow for reasonable flexibility, at most two gaps were allowed per haplotype, and their lengths were limited to one marker. These parameter values prune patterns which are not biologically conceivable (unreasonably long haplotype patterns, or those consisting mainly of gaps) and, from a practical point of view, they allow faster execution and experimenting with the method than more flexible parameters. With these parameter values, localization time for one simulated data set on a 400-MHz Pentium PC was around one minute. The association threshold for the signed ±χ² measure was set to χ = 9, on the basis of earlier work on similar data and methods (V. Ollikainen, H. Mannila, R. Kilpikari, M. Koivisto, H. Kärkkäinen, M. Mäkelä, P. Onkamo, S. Smolander, and J. Kere, unpublished data) and some experimenting. To ensure that the selection of these particular values is not critical for the method and to assess the robustness of HPM in this respect, we also experimented using patterns with unlimited length, with longer gaps, and without gaps.

Localization Accuracy

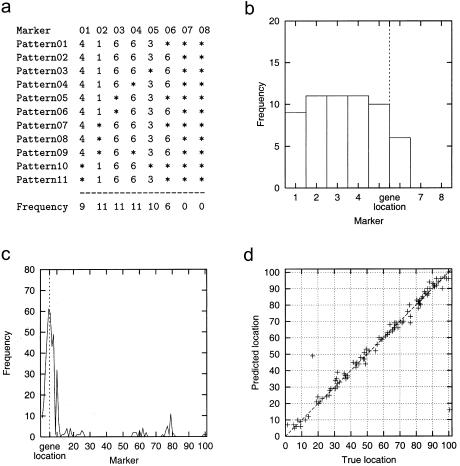
To illustrate the HPM method, figure 1a shows the list of 11 most strongly disease-associated haplotype patterns in a simulated data set with A=10% (10% of disease-associated chromosomes carry the mutation; no missing or corrupted data). The chromosome has 101 markers, but the patterns with strongest association occur between markers 1 and 6. The bottom line gives the marker frequencies for these markers, and the frequencies are also plotted as a histogram in figure 1b. Markers 2-4 have the highest frequency, closely followed by markers 5 and 1. The true gene location is in this data set halfway between markers 5 and 6 (depicted by a dashed vertical line). Figure 1c shows a frequency histogram for the same data set, but this time with all haplotype patterns exceeding the association threshold of 9. Marker 5 has now the highest frequency and is therefore predicted as the gene location; a vertical line shows, again, the true location at position 5.5.

Figure 1.

a, Examples of strongly disease-associated haplotype patterns discovered in a data set with A=10%; only the first 8 markers of 101 are shown. b, Corresponding marker frequencies (“Don’t care” symbols (*) in gaps are included in marker frequencies.) c, Marker frequencies in the same data set with all strongly disease-associated haplotype patterns. d, Plot of the true versus the predicted locations of the DS gene for 100 data sets (A=10%).

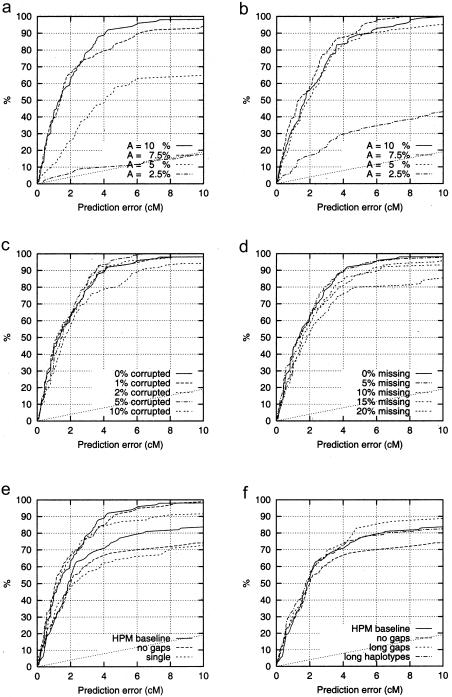
The true versus predicted locations for 100 simulated data sets with A=10% are shown in figure 1d; the data set of figure 1c is represented by a cross at (5.5, 5). Overall, the predicted location shows good agreement with the true location. The localization accuracy and the effect of phenocopies was explored in more detail by plotting curves similar to power graphs: the height of the curve shows the fraction of data sets for which the localization was successful, as a function of the allowed localization error (fig. 2a). The solid line represents the results given by figure 1d: for instance, in 90% of the simulations the error is ⩽4 cM. For A=7.5% the accuracy is near that for A=10%, but for A=5% a clear drop can be observed and for A=2.5% the localization method does not perform significantly better than random guessing. Our explicit aim was to test realistic (small sample sizes) but difficult (2.5%⩽A⩽10%) cases, in order to explore the limits of the method—which in this case and with respect to A seem to be somewhere around A=5%. For larger samples and lower phenocopy rates, the results should obviously be at least as good as those presented here.

Figure 2.

The effect of various factors on prediction accuracy. The y axis shows which fraction of simulated data sets is within the error bound given on the x axis (i.e., y=P[error ⩽ x]). The lowest, dotted curve is the prediction accuracy of random, uniform guesses. a, Effect of A, the proportion of DS mutation carrying chromosomes. b, Effect of doubled sample size (400 disease-associated and 400 control chromosomes). c, Effect of corrupted data. d, Effect of missing data. e, Comparison of prediction methods. The three topmost curves have been obtained with 0% corrupted and 0% missing data; the lower curves with 1% corrupted and 20% missing data. f, Effect of pattern search parameters. “HPM baseline”: haplotype pattern searching as before; “no gaps”: haplotype pattern searching without gaps; “single”: the middle point of single most strongly associated haplotype without gaps is used for predicting the localization; “long gaps”: gaps of up to three markers allowed, “long haplotypes”: no length limit on the pattern lengths.

The effect of sample size was examined by doubling the number of both chromosomes—that is, with data sets of 400 + 400 chromosomes (fig. 2b). Compared to the smaller data set (fig. 2a), the localization accuracy improves significantly for low values of A (A=5%, 2.5%); for larger values of A, there is not much difference. (It is a coincidence that localization accuracy seems slightly better for A=7.5% than for A=10% in fig. 2b.)

The effect of corrupted data, i.e., genotyping errors and sporadic marker mutations, was tested by randomly changing alleles in the data. Figure 2c shows the influence of having ⩽10% of data corrupted (with A=10%). Marker mutations were not modeled in simulations, but the mutation process—involving the coalescence of the mutated allele through generations to several persons with the common mutation in the final study population—should actually make the associations easier to detect than random changes of alleles do. The influence of having up to 20% missing data was explored in a similar manner (fig. 2d, A=10%). The effect of missing data corresponds to that of corrupted data, as could be expected. There is hardly any difference in the accuracy with 0%–5% of data corrupted or missing. Higher proportion (⩾10%) results in a slight decrease in performance. The combined effect of corrupted and missing data contained no surprising interactions.

The HPM method was compared to two simpler alternatives (fig. 2e, A=10%). The first one was to take the single most strongly associated haplotype without gaps and to predict the DS locus to be in the middle of that haplotype. The second was to localize with haplotype patterns without gaps. With correct data (three higher curves), there is not much difference between the performance of the methods for error bounds <4 cM. More differences appear as corrupted and missing data are introduced (lower three curves), and the HPM method seems to outperform the other methods by finding the approximately correct region more consistently.

In order to assess the robustness of the method with respect to the selection of pattern search parameters, simulated data with A=10%, 1% corrupted and 20% missing, was reanalyzed (fig. 2f). The effect of gaps in the patterns was evaluated by either prohibiting gaps (as in fig. 2e) or by allowing the gaps to be up to three markers long instead of just one. In addition, a test was run where the length of the haplotype patterns was not limited. Differences start to appear at error bounds of at least 2–4 cM; allowing longer gaps improves the performance somewhat, whereas prohibiting gaps altogether results in a decreased performance.

Localization Accuracy with Permutation Tests

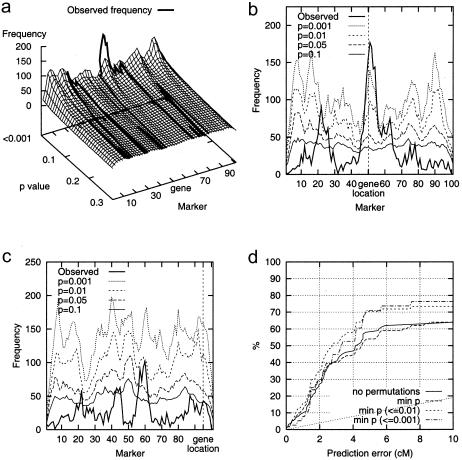
Permutation tests were used to obtain more information about the significance of observed marker frequencies. Markerwise P values were used to sort markers by their statistical unexpectedness, not to test the statistical significance of the findings. The experimental results obtained with 1,000 random permutations show that the peaks observed in marker frequencies in the vicinity of DS locus typically clearly surpass those produced by background LD. The permutation surface for a simulated data set with A=7.5% is shown in figure 3a; figure 3b gives similar information in two-dimensional form. The true DS gene location was at point 50.2, and the lowest P values, P<.001, were obtained around it at markers 46–56. Figures 3a and 3b represent a typical successful case: the marker frequency is highest close to the DS locus, and permutation tests confirm this finding. An unsuccessful localization is in turn shown by figure 3c; the highest marker frequencies and the best markerwise P value, ∼.01, are obtained for marker 60, but the true DS locus is at position 95.0.

Figure 3.

Permutation tests with a simulated data set with A=7.5%. a, The permutation surface. The height of the surface at point (i,p_i) is the marker frequency of marker m_i that has an estimated markerwise P value of p_i. The observed frequency is plotted on the surface by projecting it from the marker-frequency plane onto the permutation surface. The closer the line gets to the ‘back wall’, the more significant is the marker frequency. b, Marker frequencies for different P values. The solid line shows the observed marker frequencies in the simulated data; the dashed lines have been plotted by connecting marker frequencies for which the markerwise P values are the same. c, Marker frequencies for different P values in an unsuccessful localization. The solid line shows the observed marker frequencies in the simulated data; the dashed lines have been plotted by connecting marker frequencies for which the markerwise P values are the same. d, The effect of permutation tests on prediction accuracy, with 100 data sets where A=5%. The solid line represents localization accuracy without permutations, and the dashed lines show the prediction accuracy with the smallest marker-wise P value (“min p”), or with the smallest P value at most .01 or .001. If the smallest P value is >.01 or .001, no prediction is made at all; the fraction on y axis is computed among the predictions made. The lowest, dotted curve is the prediction accuracy of random, uniform guesses.

We performed the following experiments in order to see if the prediction accuracy can be improved by permutation tests. We predicted the location of the DS gene to be at the marker with the smallest P value instead of the most frequent marker. Optionally, given a threshold for the P value, we made a prediction only if the best P value was below the threshold (and otherwise replied “don’t know”). The localization accuracy is somewhat improved by employing permutation tests (figure 3d, A=5%). The improvement was less evident with A=7.5%, and with A=10% this modification had practically no effect. For A=2.5%, again, there is no improvement with the sample size of 100 affected individuals.

SNP Data

We performed experiments with artificial SNP data to test the utility of the HPM method with biallelic markers. An increased density of markers was used (3 SNPs per 1 cM) to maintain the overall information content roughly at the same level with the microsatellite markers. A higher density is also motivated by the willingness to increase the density of markers in an interesting region. Additionally, it is expected that genomewide scans at higher densities of SNPs will be possible in the near future. Missing information was simulated by randomly removing 12.5% of the alleles. This was done in order to mimic the effect of haplotyping ambiguities with SNP markers, expected to occur whenever a family trio, both parents and the only offspring, are heterozygous in a given locus. The pattern search parameters were modified slightly, to account for the higher density of markers; the maximum length of a haplotype pattern was 21 markers (∼7 cM). The maximum number of gaps was two, and the maximum length of a gap was one marker.

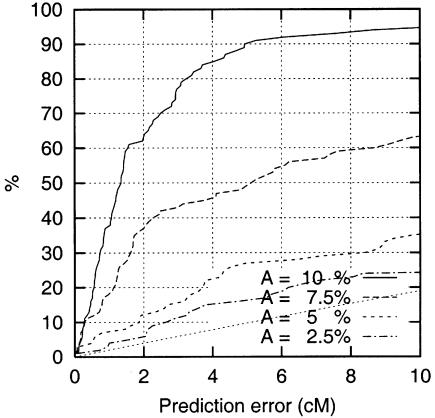
The results (fig. 4) show that the HPM method performs well with the simulated biallelic data. For A=10%, the accuracy is close to that of complete microsatellite data (fig. 2a), despite the 12.5% of missing data; with smaller values of A the accuracy drops somewhat faster than with complete microsatellite data. Overall, the localization accuracy with 3 SNPs per 1 cM in these data sets is close to that of a map with 1 microsatellite per 1 cM.

Figure 4.

Effect of A, Proportion of DS mutation–carrying chromosomes, in the SNP data.

Real HLA Data

We applied our method to a real data set, consisting of affected sib-pair families with type 1 diabetes from the United Kingdom (Bain et al. 1990) that were genotyped for 25 polymorphic microsatellite markers. These markers covered a 14-Mb region including the entire HLA complex. The HLA-DQB1 and DRB1 loci, located in the center of these 14 Mb, are known to be the primary constituents of the major type 1 diabetes–susceptibility locus mapped to this region, designated as IDDM1. This data set was originally generated to apply the currently available tools of association fine mapping, in order to investigate the accuracy this locus could be mapped with. Using the multiallelic association test T_sp (Martin et al. 1997), it has been demonstrated that the HLA-DQB1 and DRB1 loci could be mapped with surprising accuracy, despite the tremendous strength of LD in that area (Herr et al. 2000).

To test HPM in a setting similar in sample size to the simulated cases, only 200 of the original 385 affected sib-pair families were used, and one of the affected offspring was selected randomly in each family. The control chromosomes were generated by including only the nontransmitted alleles or haplotypes. HPM was applied to this data set using the same parameters as described for the analysis of the simulated microsatellite data.

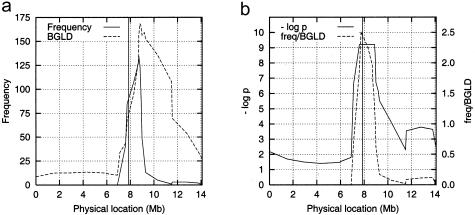
The results (fig. 5) demonstrate that the method was capable of mapping the disease locus to the marker located closest to HLA-DQB1 and DRB1, that is marker D6S2444, even though background LD in the HLA and the telomeric end of the map was very strong (Herr et al. 2000). A comparison to the results of the T_sp analysis (Herr et al. 2000) shows that the mapping accuracy was similar with both approaches even though we used less information with HPM.

Figure 5.

Results on the real HLA data. a, Marker frequencies and background LD (BGLD), as measured by the markerwise mean of the 10 highest frequencies obtained by 10,000 permutations. b, Negative logarithm of the markerwise P values. The vertical line shows the gene location. The flat interval of −log p≈9.21 is the upper limit of the score, due to the limited number of permutations. The ratio of the marker frequency to BGLD (dashed curve) was used for estimating the gene location inside this interval.

Discussion

We have introduced HPM, a new, nonparametric approach to LD mapping. We presented experimental results with realistic, simulated data with both microsatellite and SNP markers, and with real data from a complex disease in an old nonisolate population. To our knowledge, this is the first time when data mining has been shown to be a working approach in LD mapping with genetic-marker data.

The HPM method seems to offer good possibilities for fine mapping, for example in proving DS loci when multiple candidate genes are screened with a dense map of markers after finding initial positive linkage. Our results indicate that the proposed method is robust to missing and erroneous data. It is suitable for application in complex disease mapping with high etiologic (allelic and locus) heterogeneity, as it can cope with a high degree of phenocopies. The power is good even with small data sets (100 affected and 100 control individuals); however, an increase in sample size (e.g., 200 affected and 200 control individuals) increases the power considerably, especially if the proportion of mutation carrying chromosomes (A) is very low. With a moderate sample size of 200 affected individuals we were able to reliably localize genes with first-degree relative risks as low as λ=1.7.

Even though the simulation results are for a population isolate, the method itself does not require the study population to be an isolate, as the experiments with the real data show. At least moderate LD should exist between consecutive markers near the disease locus or loci, which means that the average marker distances in the region to be studied should be small with respect to the amount of LD in the study population. For a population isolate with expansive growth through ∼20 generations, as in our simulations, the average microsatellite marker distance of 1 cM throughout the area of interest gave good results. For a typical linkage result, the area to fine map is 20–30 cM, which would in a similar setting require the genotyping of 20–30 markers. To find out which kind of average marker spacing is needed in different study populations, the power of the method should be explicitly studied in different situations. A crude estimate might be obtained by relating 4Nc, the measure for average LD according to Long and Langley (1999), to the power of the localization.

Current statistical methods for LD/association mapping are based on explicit statistical models of LD distribution and likelihood analysis. If the assumed model is correct, the statistical approach is more powerful and is likely to give better estimates of the location. However, if there is no a priori information about the correct inheritance model, the model-based approach may be misleading. The models typically are based on assumptions, which may be much too restrictive in complex disease mapping, about the mode of inheritance, number, and dominance of the DS loci or the age of the mutation. The haplotypes considered in the likelihood-based methods consist of either one marker or a sequence of consecutive markers. There are practical reasons for this: explicit statistical modeling is difficult and computationally heavy, even for these simple cases. Allowing for gaps would only complicate the situation further. The difficulty of explicit statistical modeling is also the reason that these methods are more suitable for monogenic diseases than for complex ones. On the other hand, the rigid statistical models give possibilities for constructing confidence intervals for the location and test statistics for significance testing, which are not straightforward in our approach.

Topics for Future Work

Complex diseases are a major challenge for gene mapping. Most of the genes involved have very small effects. The diseases are characterized by etiologic heterogeneity; the disease may result from different combinations of factors in different families and in different populations. Environmental factors, gene-environment interactions, and gene-gene interactions (epistasis) may further complicate the genetic etiology. This heterogeneity is a major issue when searching for associations between alleles (haplotypes) and the disease status. The complexity makes the finding of DS genes very difficult for explicit statistical modeling approaches, as noted by Terwilliger and Weiss (1998), for example. The power to detect minor genes is low, even if the data include hundreds of families.

Without regard to the yet-unsolved statistical problems, association studies have recently been proposed as a powerful approach for detecting the several weak genetic effects which underlie susceptibility to complex diseases (Collins 1995; Lander 1996; Risch and Merikangas 1996). Improved techniques for high-throughput identification and genotyping of polymorphisms, such as SNPs, offer the possibility of using high numbers of markers in genome screening and candidate-gene scanning in the near future. The sufficient density of such maps, given the population history of modern human populations, has been analyzed theoretically (Chapman and Wijsman 1998; Kruglyak 1999; Long and Langley 1999).

We believe that the approach adopted here may allow analysis of some of these complex characteristics as well. As a nonparametric approach, the method has unique properties compared to other LD methods. For example, it is conceptually rather straightforward to extend the algorithm to find several genes simultaneously. The method was modified to find two genes simultaneously and was tested using simulated data with two interacting genes and phenocopies. Both DS loci were reliably localized (data not shown). The problem of multiple founder haplotypes (allelic heterogeneity in DS locus) is largely bypassed simply by counting separate patterns together in the marker scores. The handling of marker inconsistencies, such as genotyping errors and mutations, might be further improved by allowing approximate pattern matching in the haplotype pattern discovery step. The proposed method also scales well to large data sets of biallelic and multiallelic markers.

In addition to genetic marker data, information on environmental covariates is often collected. These may include nutritional factors, smoking habits, infections diagnosed on the individual etc. Quantitative measurements closely related to the disease diagnosis (which often is only a best agreement with the expert clinicians, not an obvious dichotomy between healthy and affected individuals), like immune response measurements in asthma or serum autoantigens in type 1 diabetes, etc., are also often available. These measurements might actually have a simpler genetic basis than the disease per se, as the disease state may actually result from very complicated and heterogeneous processes. Discrete nongenetic data could be included in the analysis in quite a straightforward fashion, continuous measurements should be discretized first. Finally, data-mining methods might be used as a preprocessing step for more detailed explicit statistical analysis. For example, the haplotype patterns might be used as a sample space for the reconstruction of ancestral haplotypes in DS chromosomes.

Appendix A : A Lower Bound for Pattern Frequency

Given a 2 × 2 contingency table of the numbers of disease-associated (A) and control (C) chromosomes either matching a pattern (P) or not (N), the χ² test statistic for the disease association of the pattern is defined by

where π_ij is the number of chromosomes with properties i and j, π_i the number of chromosomes with property i, and π the total number of chromosomes. Given the number of disease-associated chromosomes (π_A), the number of control chromosomes (π_C), and a lower bound x for the test statistic, we can derive a lower bound for the pattern frequency among the disease-associated chromosomes (π_AP) as follows. Assuming the pattern is disease-associated, we have π_AP·π_CN>π_AN·π_CP. The test statistic is maximized when π_CP=0, implying π_AP=π_P and π_CN=π_C. Then

and

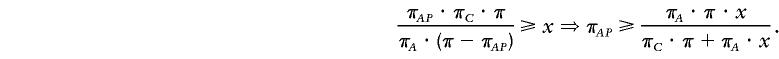The situation is symmetric for protective haplotypes, and the lower bound for π_CP is obtained by simply swapping π_A and π_C in the above result. If disease-associated and protective haplotypes are searched for at the same time, the smaller of π_AP and π_CP can be used as a lower bound for π_P, making the implementation slightly simpler.

Appendix B : Data Generation

The population generator of Populus simulator package was used to generate 100 artificial pedigrees that correspond to the population-specific demographical parameters in the history (table B1). Each of the resulting 100 very large pedigrees contains all individuals that have lived in the population since the date of foundation. Then the chromosome simulator of the Populus package was used to simulate the inheritance of pairs of homologous chromosomes within each large pedigree. Finally, when the inheritance histories of all chromosomal segments were available, markers were assigned to the original founder individuals, which allowed us to unequivocally determine the alleles of each artificial person in the current population. A related approach has been previously proposed for rapid simulations in linkage analysis (Terwilliger et al. 1993).

Table B1.

Parameters Used to Simulate Populations

Parameter	Valuea
Probability of marriage, male (ages 18–32 years)	.9
Probability of marriage, female (ages 17–31 years)	.9
Maximum age at pregnancy (years)	44
Initial age structure:
0 years	.03
1 years	.12
2–5 years	.15
6–15 years	.24
16–45 years	.40
46–75 years	.06
Proportion of descendants in initial population (by age):
0–15 years	.5
15–20 years	.5 →.3b
20–30 years	.3→.2
30–50 years	.2→0
50–75 years	0
Starting year	1500
Initial population size (in 1500)	300
Expected no. of children, by time period:
1500–1775	5.5
1776–1915	5.5→4.0
1916–2000	4.0→1.6
Immigration rate	0
Probability of death (function of birth year and age):
1400–1750:
0 years	.22
1–10 years	.10
11–25 years	.10
26–35 years	.08
36–45 years	.15
46–65 years	.25
66–85 years	.10
1751–1900:
0 years	.15
1–10 years	.085
11–25 years	.085
26–35 years	.18
36–40 years	.1
41–45 years	.05
46–65 years	.2
66–85 years	.15
1901–2000:
0 years	.05
1–5 years	.035
6–15 years	.005
16–35 years	.125
36–65 years	.18
66–85 years	.605

^aParameter values are functions of year and age of each individual.

^bAn arrow denotes linear interpolation within the given ranges.

In the simulations we assigned a single pair of chromosomes to each founder, and set the genetic length of the chromosomes to 100 cM for both males and females. The meiosis was modeled under the assumption of no chiasma interference, which corresponds to Haldane’s model.

In our simulations, we used the Finnish Kainuu subpopulation as our model population. We defined the population to have been founded 500 years ago by a group of 300 individuals, where the total number of independent founders was 198, and the remaining 102 initial settlers were their descendants. This serves as a conservative approximation, since the isolate is estimated to be founded in those times by a relatively small group of individuals migrating from the south (de la Chapelle 1993; de la Chapelle and Wright 1998). For the 100 pedigree replicates, the size of the final population varied between 67,467 and 136,613 individuals; the average size was 101,475, which corresponds well to the current size of the isolate.

In each simulation, a sample of 100 affected and 100 control individuals was picked by a slightly nontrivial procedure. Since we wanted to fix the disease model to a relatively common disease with a dominant model and high phenocopy rate in respect to any single disease-predisposing locus, we decided to set the mutation prevalence to 6/1,000. Thus, in each simulation, the aim was to have ∼600 affected mutation carriers in the final population. To compute the mutation source and locus in a computationally effective way, we first selected 30 random points in the 100-cM chromosomal region that were considered as possible mutation loci. This selection was repeated in each iteration. After the chromosomal segment data were generated, the resulting prevalence for each possible combination of a founder chromosome and a mutation locus was computed. We then picked a combination that produced the desired overall mutation prevalence of 6/1,000 in the final population as accurately as possible. Since there were 198 unrelated founder individuals and 30 possible mutation loci, a total of 11,880 possible source/locus pairs were considered in each iteration, which turned out to be more than enough to produce the desired mutation prevalence accurately. Out of the ∼600 resulting affected carriers, we then picked random samples of 20, 15, 10, and 5 individuals to produce mutated chromosome frequencies of A = ∼10%, ∼7.5%, ∼5%, and ∼2.5%. The rest of the affected sample was chosen from noncarrier individuals to produce the phenocopies. No siblings were allowed to appear in the samples.

It is well known that in case-control studies, closer kinship in the affected sample may cause false positive results because of extra background linkage disequilibrium everywhere in the genome (Terwilliger and Weiss 1998; Hovatta et al. 1999). To overcome this problem, we used family-based pseudocontrol chromosomes. This was done in practice by taking the alleles in the nontransmitted chromosomal segments of the parents of each affected individual and labeling them as control chromosomes. In each simulation, a total sample of 400 chromosomes was taken, of which 200 were affected and 200 control.

We treated the haplotypes obtained from the simulator as given, which corresponds to error-free haplotyping. (However, this is not in any way a prerequisite for applicability of the method, as is demonstrated in experiments with missing and erroneous data.) The entire sampling procedure corresponds to a standard case-control study setup with a pseudo-control sampling approach, where a dominant disease with high prevalence (0.03–0.12) is observed, and the phenocopy rate is high, but unknown at the time.

To accommodate the fact that ever-increasing informativeness of marker maps may soon facilitate whole-genome LD mapping, we used relatively dense and informative marker maps with intermarker intervals of exactly one cM. Since the usefulness of a marker depends solely on its informativeness, we did not want to fix the number of alleles in each marker but instead fixed the informativeness of every marker to 0.7, as measured by the polymorphism information content (PIC). Typically, each generated marker contained 4–8 alleles, whose frequencies were less equally distributed as the number of alleles increased. The markers were created using a brute-force algorithm, where large numbers of markers with variable allele frequencies were produced, but only the small minority with desired PIC was approve.

Data sets used in this study are available electronically (see Electronic-Database Information).