Testing the Robustness of the New Haseman-Elston Quantitative-Trait Loci–Mapping Procedure

Abstract

Variance components (VC) techniques have emerged as among the more powerful methods for detection of quantitative-trait loci (QTL) in linkage analysis. Allison et al. found that, with particularly marked leptokurtosis in the phenotypic distribution and moderate-to-high residual sibling correlation, maximum likelihood (ML) VC methods may produce a severe excess of type I errors. The new Haseman-Elston (NHE) method is a least-squares–based VC method for mapping of QTL in sib pairs (Elston et al.). Using simulation, we investigate the robustness of the NHE to marked nonnormality, by means of the same distributions and worst-case conditions identified by Allison et al. for the ML approach (i.e., 100 pairs; high residual sibling correlation). Results showed that, when marked nonnormality is present, the NHE can be used without severe type I error–rate inflation, even at very small alpha levels.

Mapping of genes for complex traits requires that investigators have the most powerful statistical tests available at their disposal. In the context of a sib-pair study, variance components (VC) models with maximum likelihood (ML) testing are used to detect quantitative-trait loci (QTL). In a recent simulation study, Allison et al. (1999) found that, on the basis of the likelihood-ratio test (Fulker and Cherny 1996), marked leptokurtosis and moderate-to-high residual sibling correlation resulted in excessive type I errors for a VC QTL detection test. This study evaluates the robustness of the “new Haseman-Elston test” (NHE) that models the VC by ordinary least squares (OLS) (Elston et al., in press), rather than by ML.

The NHE entails regressing the cross product of the siblings’ mean centered phenotypes on the proportion of alleles that the pair shares identical by descent (IBD); that is, one fits the following regression model: 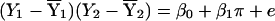, where Y₁ is the phenotype of the arbitrarily defined first sib in a pair, Y₂ is the phenotype of the arbitrarily defined second sib in a pair, 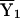is the sample mean of Y (the phenotype) among the first sibs, 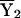is the sample mean of Y among the second sibs, π represents the proportion of alleles that a pair shares IBD, e is a residual or error term for unexplained variation, β₀ is the residual sibling covariance (induced by other genetic and shared environmental influences), and β₁ is the additive genetic variance due to the QTL. After the slope is constrained to be nonnegative, testing the null hypothesis (H₀: β₁=0) is equivalent to testing whether the variance due to the QTL is equal to 0. This can be accomplished using a one-tailed significance test.

It is plausible that the NHE will be more robust than the ML-based VC test, because it is based on OLS regression. In using the OLS-based NHE, one tests the significance of the QTL by dividing the sample estimate of β₁ by its standard error and assumes that, under the null hypothesis, the results will be distributed as t with N-2 df, where N is the number of sibling pairs. This assumption will be met if either of two conditions holds: (1) the population residuals from the NHE regression model are normally distributed, or (2) the mean and the variance of the population residuals from the NHE regression model are finite and the sample size is sufficiently large to ensure that the sampling distribution of the sample estimate of β₁ is normally distributed by the central-limit theorem.

Research suggests that, with many commonly encountered nonnormal distributions, OLS methods are quite robust in terms of type I error rate, with sample sizes of ⩾100 (Sawilowsky et al. 1992). Thus, our design used a sample size of 100 sibling pairs and a residual sibling correlation (r) of .5 as a “boundary condition,” reported as leading to the highest type I error rates for the Fulker and Cherny (1996) ML procedure (Allison et al. 1999). Also, the use of 100 sib pairs probably represents the lower limit of reasonable sample size for sib-pair studies of quantitative traits. IBD status for the sib pairs (π from model 1) was generated, independently of the dependent variable, from a binomial distribution with n=2 and P=.5, where n represents the number of alleles and where P is the probability of alleles being IBD. For convenience, we assumed that we were working with perfectly informative markers.

For comparability to the study by Allison et al. (1999), 13 different distributions were studied. Table 1 shows the population means, variances, skewness, and kurtosis values for the marginal phenotypic distributions and for the mean centered cross products (CPs) for each condition. For each distribution, 100,000 simulated data sets (S) were produced and analyzed, under the null hypothesis of no linkage at the marker locus. Data were generated with the SAS RANNOR function (SAS release 7.0 [SAS Institute 1998]). Linkage was then tested at nominal one-tailed α values of .10, .05, .01, .001, and .0001.

Table 1.

First Four Moments of Sibling Phenotypic Distributions and CPs of Studied Distributions (S = 100,000)

	Sibling Phenotypea				Sibling CPb
Model	Mean	Variance	Skewness	Kurtosis	Mean	Variance	Skewness	Kurtosis
Normal	0	1	0	0	.498	1.259	2.436	12.080
Mixture 1	.118	1.333	.587	1.253	.611	2.936	4.728	34.364
Mixture 2	1.00	1.500	.000	−.111	.754	2.758	2.139	8.138
Mixture 3	.088	1.333	.805	2.467	.617	3.736	6.124	65.524
(G×E) mixture 1	0	2	2	14	.792	15.794	17.214	495.632
(G×E) mixture 2	1	5	.537	1.04	2.349	37.913	3.714	27.274
(G×E) mixture 3	0	2	3	25	.754	21.596	25.145	929.652
χ2 df=2	2	4	2	6	1.979	58.524	11.295	255.341
Laplace	0	2	0	3	1.009	8.916	6.287	86.906
Binary (.5)	.5	.25	0	−2	.083	.056	−.706	−1.501
Binary (.1)	.1	.09	2.67	5.11	.023	.022	4.654	21.436
Extremes	0	3.249	0	−1.727	3.508	2.003	1.766	5.024

^aValues were obtained analytically.

^bValues were obtained by simulation.

First, we validated the program by simulating the data in which the dependent variable (i.e., the CP) was normally distributed, so that the observed empirical α value would match the nominal α value. For the second condition, we simulated data from a bivariate normal phenotypic distribution with a residual correlation of .5 under the null hypothesis, with the CPs as the dependent variable. The NHE assumes that the CPs of sibling mean centered phenotypes are univariate normal; however, the CPs cannot be univariate normal if the phenotypes themselves are normally distributed. Thus, in the case of the NHE, a primary source of nonnormality is the very act of taking CPs.

Several other reasons for nonnormality of the phenotypes exist (see Allison et al. 1999). The presence of “major” genes or oligogenes, which create mixed nonnormal distributions (Schork et al. 1996), was assessed by three mixture distributions due to a biallelic segregating QTL not at the locus under study (Y=G+R, where G is the mean of the genotype at the QTL and R is the normally distributed residual term). In mixture 1, a recessive mode of inheritance was modeled in which the frequency of the increasing allele was .20. For mixture 2, the mode of inheritance was additive, and the two alleles had a frequency of .50. Mixture 3 represented a recessive mode of action in which the increasing allele had a frequency of .15. For each of the mixtures, the within-genotype residual distribution was normal, with a variance of 1.0.

Nonnormality due to gene by environment (G×E) interaction (either interaction between a major or oligogene and the environment or between a polygenic component and the environment) and epistasis (Pooni et al. 1976) was simulated by addition of an interaction term to each of the previously discussed mixture models: Y=G+R+G×R. For these simulations, the residual correlation (expressed as the correlation in the R component) and the phenotype correlation will not necessarily be equal after adjustment for the QTL genotype effects. Moreover, the amounts of variance accounted for by the QTL in G×E mixture 1, G×E mixture 2, and G×E mixture 3 were 7.14%, 10%, and 7.14%, respectively.

To study the effect of intrinsic nonnormality of the phenotype, the marginal distribution of each sibling was set to be χ² with 2 df, which represents a markedly skewed phenotypic distribution and a standard Laplace distribution (a symmetrical but leptokurtic distribution) (Evans et al. 1993). In the study of the effect of dichotomous distributions (i.e., diagnosis of disease X), the parameters underlying mixture 2, described above, served as the basis for the simulation by choosing the cut points necessary to produce two Bernoulli distributions: one symmetrical, with a probability of being affected (P_A) that is equal to .5; and one skewed, with P_A=.10. Once the data were dichotomized for a population residual correlation of .50, the expected sample phenotypic correlation values for P_A=.5 was .34, and for P_A=.10 was .25.

Nonnormal distribution obtained from extreme selective sampling, which follows the “extreme discordant and concordant sib-pair” design (Dolan and Boomsma 1998), was simulated by selection of sib pairs in which neither phenotypic value was located between the 90th and the 10th percentile of a bivariate normal distribution, with a population correlation of .50. Data generation continued until sample size equaled 100 sib pairs. As a consequence of this data-generating strategy, the expected value of the sample correlation increased to .92, meaning that concordant sib pairs constituted the majority of the sample.

In terms of assessment of the empirical type I error rates for the NHE test, sampling error was taken into account by construction of an interval 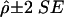, where 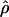is the empirical proportion of rejections and SE is the standard error. With a large sample approximation, 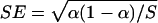, where α is the nominal level of significance and S is the number of simulations.

Table 2 displays the results of the simulations for the 13 different distributions. When normal data were simulated as a test of the validity of the software, type I error rates were consistent with the nominal α values, except for α = .01. This apparent inflation presumably corresponds to sampling error. For the CP of normal phenotypes (CP-normal), type I error rates were consistent with the nominal α values.

Table 2.

Type I Error Rates for Different α Values in the Different Distributions

	Type I Error Rates for α =
Model	.10	.05	.01	.001	.0001
Normal	.09901	.04934	.0120a	.00091	.00008
CP-normal	.10080	.05073	.00983	.00096	.00010
CP-mixture 1	.10255a	.05005	.00914b	.00067b	.00004
CP-mixture 2	.10050	.04970	.00974	.00092	.00006
CP-mixture 3	.10410a	.04977	.00773b	.00053b	.00003b
CP-(G×E) mixture 1	.10928a	.04816b	.00621b	.00045b	.00002b
CP-(G×E) mixture 2	.10181	.05052	.00911b	.00070b	.00004
CP-(G×E) mixture 3	.11350a	.04668b	.00650b	.00040b	.00001b
CP-χ2 df = 2	.10776a	.05017	.00703b	.00026b	.00001b
CP-Laplace	.10250a	.05020	.00843b	.00051b	.00001b
CP-binary (.5)	.09898	.04849	.00981	.00098	.00009
CP-binary (.1)	.10613a	.05060	.00679b	.00026b	.00000b
CP-extremes	.09868	.04925	.00975	.00084	.00008

^aAbove the upper bound of the confidence interval (inflated type I error rate).

^bBelow the lower bound of the confidence interval (conservative type I error rate).

For the CPs of the mixture distributions, the rejection rates for mixture 2 were consistent with the nominal α values. The type I error rates of mixtures 1 and 3 were somewhat conservative toward the tails of the distribution; that is, the proportions of rejections were well below the nominal α values of .01, .001, and .0001. Consistent with other simulation studies using OLS-based statistical models (e.g., Wilcox 1998), these findings may be considered a consequence of the skewed, leptokurtic distribution of mixtures 1 and 3, as compared with mixture 2 (see table 1).

When a G×E component was added to the mixtures, mixtures 1 and 3 produced some inflation of the type I errors for α=.10 and a more conservative pattern for α=.05, .01, and .001 (and even .0001 for mixture 1). For mixture 2, a conservative pattern was noticed for α=.01 and α=.001. Conservative results at these same α values were observed in the χ², Laplace, and binary distributions. In all other cases, the expected type I error rate corresponded to the nominal α.

Results of these simulations indicated that, even under conditions of moderately small sample sizes, strong residual correlation, and marked nonnormality, the NHE test was quite robust; that is, even in these “worst case” scenarios, the NHE test held the empirical type I error rate at or below the nominal α value. Moreover, we repeated all simulations described herein with 50 sib pairs, and we observed results that remained conservative (data not shown). In fact, with nonnormality, results tended to be conservative for smaller α values. Although this might be expected by appeal to the central-limit theorem and knowledge of previous studies of robustness involving tests based on OLS procedures (e.g., see Wilcox 1998), these results stand in marked contrast to those obtained with an ML-based test of the same hypothesis under the same conditions (Allison et al. 1999).

It must be pointed out that these results can be generalized with certainty only to the conditions of this study. It is not certain that this degree of robustness would still be obtained if different pedigree structures, nonindependent sibling pairs, different distributions, or <50 sibling pairs were used. On the basis of other results (Allison et al. 1999), one would not expect less robustness with a lower residual correlation. It is possible that, if the residual correlation were >.5, the degree of robustness might not be as strong, although, in our experience, sibling correlations >.5 are uncommon. Moreover, the NHE was robust, given the smaller α values (e.g., .01, .001, and .0001) commonly used in genetic research. In disciplines where α = .10 is more common, OLS-based procedures such as the NHE would not be considered robust, given the distributions simulated in this study.

The NHE test is simple to implement and can be easily used in standard statistical software such as SAS or SPSS. For multivariate linkage studies, the NHE may be especially useful as the number of phenotypes increases. A multivariate version of the NHE can be adapted, just as it is possible to adapt the original Haseman-Elston test (Allison et al. 1997; Amos and Laing 1993). Although an ML framework is flexible in allowing for multivariate testing, as the number of phenotypes grows large, the number of parameter estimates increases by m+1, where m is the number of phenotypes studied. In contrast, with each additional phenotype, the number of parameters to be estimated by the NHE test will increase only by 1. Thus, with multivariate testing, the NHE may be far more computationally tractable and efficient. Even with univariate testing, the difference in computation speed for the two approaches is dramatic.

It should be pointed out that the OLS solution that comprises the NHE test and the standard ML implementation are not the only options for implementation of VC tests for QTL mapping (see Allison et al. 1999); for example, some investigators are working on implementations of VC QTL procedures in an ML framework in which the data are assumed to be sampled from a multivariate t distribution with k df, where k is a parameter to be estimated. Therefore, although the current results clearly show that the NHE was robust in that type I error rates were not inflated, the more conservative trend toward the upper tail of the referent distribution suggests that it may have low statistical power in many of the situations simulated in this study. Thus, in terms of robustness to violations of normality and residual correlation as well as of statistical power, further research is needed to evaluate how the NHE compares with other QTL-mapping VC procedures.