Introduction
In recent years, the development of new methodology and/or the improvement of existing methodology in gene mapping, specifically that which is targeted toward the localization of genes underlying complex disorders, have led to a proliferation of linkage analysis techniques, most of which have been implemented in user-friendly programs and have been made freely available to the genetics community. A scan through genetic epidemiological journals reveals the almost immediate embracement of these techniques; however, user interpretation regarding the statistical properties of these tests is often insubstantial and occasionally is incorrect. To assist in this interpretation, this review provides both an overview of the underlying hypotheses and an explanation of the different statistical properties of the most-popular techniques. Furthermore, accepted thresholds for genomewide significance and appropriate corrections for multiple testing are discussed.
Traditional LOD-Score Method
Traditional parametric linkage analysis, commonly known as “logarithm-of-odds” (LOD-score) analysis, is based on the likelihood (odds) ratio, which is the ratio (relative probability) between the probabilities of two alternatives LHA/LH0, where LH0 is the likelihood under the null hypothesis of no linkage (recombination fraction [θ] .5) and where LHA is the likelihood of the alternative hypothesis of linkage (θ<.5). For a given set of pedigree genotype data, the likelihood of producing the observed data is calculated given a set of assumptions about the parameters of the underlying genetic model. These parameters include the allele frequencies of the loci involved, the relevant penetrance values, and the θ between loci. Taking the log10 of LHA/LH0 produces the familiar LOD score (Morton 1955). The maximum LOD score (MLS) is thus obtained by testing across different values of θ.
Maximum likelihood–ratio statistics are asymptotically distributed as χ2 values with degrees of freedom equal to the difference in the number of parameters estimated/maximized in the numerator compared with the number of those estimated/maximized in the denominator. In the case of the standard LOD score, θ is maximized in the numerator, whereas in the denominator θ is fixed at .5. However, when testing for linkage is done, the test is declared significant only when 0<θ<.5, thereby reducing the distribution to one tail. Subsequently, the pointwise significance (P value) of a LOD score can be determined using the formula P(LOD)=.5×(χ21>2ln10×LOD), since, under the null hypothesis of no linkage, the asymptotic distribution of a LOD multiplied by twice the natural logarithm of 10 (2ln10, or ∼4.6) is a 50:50 mixture of a point mass at 0 and a χ2 distribution with 1 df (χ21).
Traditionally, a LOD score of >3 has been deemed to indicate significant linkage. A LOD score of 3 indicates that the odds that the loci are linked are 1,000 times greater than the odds that they are not. However, if one randomly chooses two loci in the human genome, those loci are ∼50 times (i.e., 44 autosomes plus two sex chromosomes) more likely to be on different chromosomes. Therefore, even though the data may be 1,000 times more likely to have arisen under linkage compared with nonlinkage, the fact that nonlinkages are 50 times more common than linkages implies that a LOD score of 3 corresponds to odds that are ∼20:1 in favor of linkage. That is, a LOD score of 3 will prove to be spurious in ∼1/20 instances (P=.05). Building on the earlier work of Morton (1955), Lander and Kruglyak (1995) performed calculations based on the mathematical theory of large deviations (Lander and Botstein 1989; Feingold et al. 1993), and they determined that, with the use of LOD-score analysis in human pedigrees, in which the total meiotic crossover rate between genotypes compared is set at one, an exact genomewide significance threshold of P=.05 is achieved at a pointwise P value of P=4.9×10-5, which is equivalent to a LOD score of ∼3.3. They also introduced a pointwise P-value threshold of P=1.7×10-3 (LOD score 1.86) as evidence for suggestive linkage—that is, statistical evidence expected to occur one time at random in a genome scan. Alternatively, other regions of potential interest may be identified using a nominal pointwise threshold of P=.05, which is equivalent to a LOD score of 0.5875.
LOD-score analysis is the most powerful linkage analysis technique when the parameters of the genetic model are known. However, the use of conventional LOD-score methods for analysis of the contribution of genetic factors to complex diseases, for which questions exist regarding disease definitions and the mode of inheritance, leads to an increase in the chance of making a false rejection of linkage (Risch 1990b). Techniques that may be used as alternatives to parametric LOD-score analyses determine allele sharing among affected relatives. Although certain assumptions about the underlying genetic model are made by these methods, allele-sharing techniques are denoted as “nonparametric” since they do not require specification of a genetic model (see Whittemore 1996). In this issue of the Journal, Ott and Hoh (2000) provide a general overview of statistical methods for disease-gene mapping.
Allele-Sharing Methods
The most common allele-sharing technique is the affected-sib-pair (ASP) test, which compares the observed number of ASPs sharing zero, one, or two alleles identical by descent (IBD) with that which is expected under no linkage (proportioned .25:.5:.25). The general approach of ASP analysis is described in figure 1, in which, for simplicity, it is assumed that all four parental alleles can be distinguished. However, restriction of the ASP test to such “fully informative” families will undoubtedly result in a loss of information, because both parents will not always be heterozygous with different genotypes. In such cases, IBD sharing may be equivocal, with sib pairs possibly sharing or not sharing alleles, but their absolute values cannot be directly determined from the observed genotype data. Subsequently, likelihood methods were introduced to provide a satisfactory way of dealing with data for which IBD status cannot be unequivocally determined for all ASPs.
Figure 1.
Nuclear family with an ASP showing IBD-sharing possibilities for a marker where all four parental alleles, denoted as “1,” “2,” “3,” and “4,” can be distinguished. By fixing the first sibling’s genotype (1/3) and by listing the other sibling’s possible genotypes (2/4, 2/3, 1/4, and 1/3), it can be seen that, under Mendelian inheritance (i.e., LH0), siblings are expected to share zero, one, and two alleles with a probability of 25%, 50%, and 25%, respectively. The ASP LOD score is calculated as log10(LHA/LH0). For example, in a population of 100 ASPs, if 10 pairs shared zero alleles (z0=10/100), 50 pairs shared one allele (z1=50/100), and 40 pairs shared two alleles IBD (z2=40/100), then LHA =.110×.550×.440 and LH0 =.2510×.550×.2540. Thus, log10(LHA/LH0) = log10(1.074×10-41/7.007×10-46)=log10(15,325)=4.19.
The main approach of current ASP analyses is the likelihood-ratio method of Risch (1990b, 1990c), which maximizes the likelihood of incompletely polymorphic genotype data with respect to the probabilities of sharing zero, one, or two alleles IBD. Maximization of observed sharing probabilities is performed, using an E-M (expectation-maximization) algorithm (Dempster et al. 1977), by restricting z1 to .5 and z0⩽.25 (or, equivalently, z2⩾.25), where z1 and z0 are the sharing of one and zero alleles IBD, respectively. By fixing z1 at .5, the test follows an additive model and assumes no dominance variance. An additive model assumes that the genetic component of a trait’s phenotypic variance is due to the additive effects of genes at different loci. Subsequently, this model approximates genetic heterogeneity and allows for no interaction between loci (Risch 1990a). Dominance variance occurs when alleles at a locus exhibit dominance-recessive interactions, in which the effect of one allele at a locus is masked by the effect of the other allele. In the special case of siblings sharing both copies of alleles, these siblings will share any dominance relations between the two alleles. Therefore, sharing a similar dominance configuration will also increase the resemblance between siblings. Furthermore, because only one parameter (z0) is maximized in the numerator, an MLS obtained in this way has the same asymptotic distribution under the null hypothesis as does the standard LOD score (Risch 1990c; Holmans 1993).
Later, Holmans (1993) and Faraway (1993) independently showed that maximization of the likelihood ratio in this way could result in parameter values that are not biologically plausible. Risch (1990b) showed that the sharing proportions (z0, z1, and z2) can be expressed in terms of relative risks, by the equations z0=.25/λs, z1=.5λo/λs, and z2=.25λm/λs. The λs, λo, and λm symbols represent the relative risk for a sibling, offspring, and MZ twin of a proband, respectively, where λs/o/m denotes the risk (affection probability) to the sibling/offspring/MZ twin of a proband, divided by the population prevalence. With relative risks expressed in terms of population and dominance variances, it can be shown that λo⩽λs and λm⩾λs (James 1971; Risch 1990a), thus restricting the set of valid sharing proportions to a triangle in the (z0,z1) plane, bounded by the lines z0=0, z1=.5, and z1=2z0. Therefore, Holmans and Faraway suggested that maximization be restricted to the set of sharing probabilities consistent with these possible genetic models; denoted as the “possible triangle” (PT), the set is defined by z1⩽.5 and z0⩽.5×z1.
Restriction to the PT follows a multiplicative model—representing epistasis (interaction) among loci—allows for dominance variance, and has been shown to increase the power of the likelihood-ratio test (Holmans 1993; Holmans and Clayton 1995). Hence, this approach would seem to be more suited to the analysis of complex genetic disorders, for which multiple interacting genes are thought to underlie susceptibility. MLSs obtained in this way (MLSPT) are mixtures of χ2 distributions with 0, 1, and 2 df under the null hypothesis. The exact mixing proportions are complicated and depend on allele frequencies, but they are ∼.402χ20, .50χ21, and .098χ22 (Holmans 1993; Knapp 1997, pp. 150–151; Sham 1998, p. 110). Hence, to obtain the nominal threshold of P<.05, an MLSPT>.74 is required, where P(MLSPT)=.5×P(χ21>2ln10 × MLSPT) + .098 × P(χ22>2ln10 × MLSPT). Moreover, when allele-sharing methods are used in human sib pairs, for which the crossover rate is 2 (i.e., LOD-score analysis in pedigrees concentrates on inheritance between two parents and one child, whereas ASP analysis has twice the potential for crossover, because inheritance from the parents now involves two children), evidence for genomewide suggestive (P=7.4×10-4) and significant (P=2.2×10-5) linkage (Lander and Kruglyak 1995) is reached at MLSPT values of 2.45 and 3.93, respectively. The popular ASP analysis programs ASPEX (Hauser et al. 1996), MAPMAKER/SIBS (Kruglyak and Lander 1995), and SPLINK (Holmans 1993; Holmans and Clayton 1995) perform these ASP tests.
Although, because of their obvious inheritance pattern, X-linked disorders are normally easier to analyze than are autosomal disorders, evidence for heterogeneity and uncertainties regarding penetrance values may make a “nonparametric” approach desirable. Additionally, when a genome scan is performed, it would be useful to ascertain the significance of X-linked markers, in a manner analogous to that used for autosomal markers. Cordell et al. (1995) extended Holmans’ method to X-linked data, showing that it was not appropriate to combine data from brother-brother (bb), sister-sister (ss), and brother-sister (bs) pairs; instead, they introduced a statistic that considers the three groups separately by restricting the maximization to the following genetically valid values: 0⩽z1bb⩽.5, 0⩽z1ss⩽.5, and 0⩽z1bs⩽.5, where z1 represents IBD sharing of maternal alleles. The sum of these three MLS statistics, known as “X-MLSPT,” is a mixture of χ2 distributions with 1, 2, and 3 df, where
 |
Therefore, to obtain the nominal threshold of P<.05, an X-MLSPT>1.18 is required, whereas evidence for suggestive and significant linkage is reached at X-MLSPT values of 3.06 and 4.62, respectively. Only MAPMAKER/SIBS (Kruglyak and Lander 1995) has the PT restriction implemented in this manner. Other ASP programs analyze X-linked data by simply summing all maternal IBD sharing together, so that, under the null hypothesis, z0=z1=.5, and the likelihood is maximized with respect to only one parameter (i.e., z0<.5 or, equivalently, z1>.5), thus giving this (X-)MLS the same properties as the standard LOD score.
Another powerful ASP technique is the mean (t2) test (Blackwelder and Elston 1985), which measures the mean proportion of IBD allele sharing and compares it with that which is expected under the null hypothesis (50%). The test statistic has, asymptotically, a standard normal distribution under the null hypothesis, and, because the alternative hypothesis of linkage is given when IBD sharing is only >50%, the test is one sided. Therefore, accurate P values can be obtained by use of a one-sided t-test, as implemented in the SIBPAL program (S.A.G.E.). It was later shown by Knapp et al. (1994) that the mean test is equivalent to a parametric LOD score obtained under a recessive model, in which the parents are either phenotype “unknown” or (equivalently) are unaffected and in which the penetrance is set close to zero. The SIBPAIR program is based on this technique and thus produces a standard LOD score.
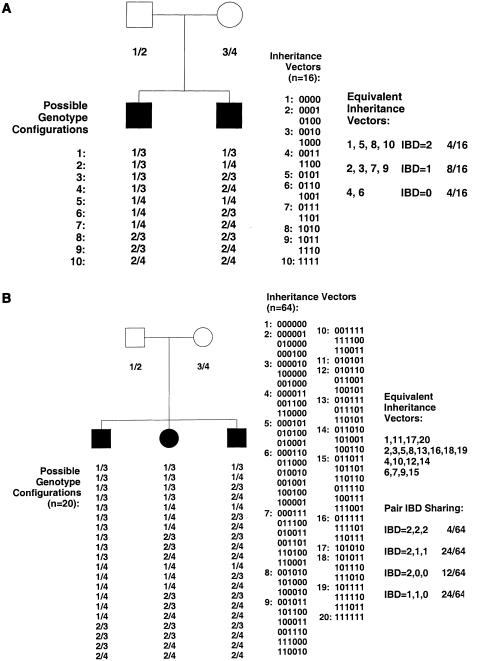
Other popular allele-sharing analysis programs include GENEHUNTER (Kruglyak et al. 1996), GENEHUNTER-PLUS (Kong and Cox 1997), and ALLEGRO (Gudbjartsson et al. 2000), which are also capable of analyzing allele sharing between more-distant relatives by counting all possible inheritance vectors. By calculation of the inheritance-vector distribution conditioned on observed genotype data, the probability distribution is concentrated on certain inheritance vectors—that is, the (likely) inheritance (IBD) pattern(s) is (are) determined (Lander and Green 1987). Figure 2 demonstrates how analysis of allele sharing can be extended to multiple relatives.
Figure 2.
A, Nuclear family with two affected siblings—identical to that shown in figure 1. B, Nuclear family with three affected siblings. Both pedigrees show the possible genotype configurations for a marker where all four parental alleles can be distinguished. The genotypes are denoted as “1,” “2,” “3,” and “4,” and are written in paternal/maternal order. These genotype configurations may also be represented as vectors, where 0 or 1 represents transmission of the paternal or maternal allele, respectively. Representation of inheritance patterns as vectors facilitates their interpretation by computer programs. For example, in panel A, (0,0,0,0) indicates that both siblings have inherited the (grand)paternal allele from both parents, whereas (1,1,1,1) indicates that both siblings have inherited the (grand)maternal allele from both parents. Also, (0,0,0,1) and (0,1,0,0) both indicate that one sibling has inherited one (grand)paternal allele from the father and one (grand)maternal allele from the mother, whereas the other sibling has inherited the (grand)paternal alleles from both parents. Inheritance-vector probabilities may be calculated by enumerating over all possibilities and may subsequently be used in tests examining allele sharing between any set of affected relatives.
GENEHUNTER calculates a nonparametric linkage (NPL) score on the basis of either the Spairs (Weeks and Lange 1988) or Sall statistic (Whittemore and Halpern 1994). Spairs measures the number of alleles shared IBD by a pair of affected relatives, whereas Sall captures information regarding the sharing between larger sets of affected relatives. Basically, Sall calculates the observed IBD probability over all possible configurations and puts extra weight on families in which three or more affected individuals share the same allele. For sibships with only two affected siblings, the two statistics are equal, but, for Sall, sharply increasing weight is given to families as the number of affected individuals sharing a particular allele increases. The Sall statistic is best suited to analysis of dominant loci, since more affected individuals per family are likely to share the same allele with this type of inheritance. Under the null hypothesis and when many similar pedigrees are analyzed, an NPL score is a normally distributed statistic with mean zero and variance one; however, when calculated from a small sample size and/or from pedigrees differing in size, the asymptotic properties of the NPL statistic are unreliable. Therefore, sample-specific NPL significance (an exact P value) is determined using simulation, by means of enumerating (counting of) all possible inheritance vectors and by obtaining the NPL-score distribution under no linkage. However, when inheritance information is imperfect, the variance of the NPL score is <1, thus making the test conservative. Put simply, because the true inheritance pattern is not always known with certainty but significance is evaluated using the null distribution expected in the case of complete informativeness, the NPL score will tend to be conservative, since it will be averaged across the likely inheritance patterns. The degree of conservativeness depends on the number of untyped individuals, marker heterozygosity, and, when multipoint calculations are performed, marker spacing.
To resolve the conservativeness of the NPL statistic when IBD information is incomplete, Kong and Cox (1997) proposed a likelihood approach, which has subsequently been implemented in the GENEHUNTER-PLUS (Kong and Cox 1997) and ALLEGRO (Gudbjartsson et al. 2000) programs. These programs both produce nonparametric LOD scores by maximization of a single parameter (δ) in the numerator, on the basis of observed genotype data. The δ represents the degree of allele sharing in a pedigree, where, under the null hypothesis, δ=0 and δ>0 corresponds to the alternative of excess sharing. Therefore, these nonparametric LOD scores are asymptotically distributed in the same manner as the standard LOD score.
Extended LOD-Score Methods
Recently, there have been a number of studies indicating that LOD-score (parametric) models can be more powerful than “nonparametric” techniques, as long as the mode of inheritance is at least approximately correct. In particular, LOD scores are calculated under a simple dominant (e.g., 50% penetrant) as well as a simple recessive model (Vieland et al. 1992; Durner et al. 1999), with allowance for locus heterogeneity (Barrett et al. 1999), after which the highest score is reported (Greenberg 1989; Hodge et al. 1997). However, heterogeneity (admixture) LOD (HLOD) scores obtained in this way, whether single- or multipoint, are a mixture of χ2 distributions with 1 and 2 df, resulting from the introduction of an additional free (heterogeneity) parameter. In addition, these scores require a correction for testing two inheritance models. The χ2 distribution mixtures are quite complicated; instead, a Bonferroni-type correction (Terwilliger and Ott 1994, pp. 237–238), which is approximately accomplished by adding .3 (i.e., log102) to the significant linkage threshold, is suggested. Alternatively, the standard LOD-score pointwise asymptotic P value should be doubled. Analogously, the P value should again be doubled to correct for the testing of two inheritance models, since testing the same data with two inheritance models increases the type I error. Clearly, the use of P values greatly facilitates adjustment for such multiple-hypothesis testing. Subsequently, analyses using this “MMLS/het” statistic require a corrected pointwise nominal P value of <.0125 (MMLS/het>1.09). Furthermore, P<1.85×10-4 (MMLS/het>2.75) and P<5.5×10-6 (MMLS/het>4.2) are required for suggestive and significant linkage, respectively.
Conclusions
Although only a few different statistical tests have been outlined in this review, it has been clearly demonstrated that LOD scores may vary greatly in their statistical properties and, therefore, in their level of significance. To graphically demonstrate this, the required LOD-score values for common significance thresholds have been calculated (table 1) for the different statistical techniques discussed here. As shown in table 1, the differences can be quite substantial, with some thresholds differing by 1 LOD unit. Moreover, because of these differences, care must be taken to quote the relevant genomewide significance thresholds for the analysis technique used.
Table 1.
Required LOD-Score Values for Common Significance Thresholds
| Significance Threshold | LOD/MLS | MLSPT | X-MLS PT | MMLS/het |
| P<.05 | .59 | .74 | 1.18 | 1.09 |
| P<.01 | 1.18 | 1.38 | 1.90 | 1.71 |
| P<.005 | 1.44 | 1.66 | 2.21 | 1.99 |
| P<.001 | 2.07 | 2.32 | 2.93 | 2.63 |
| P<7.4×10-4a | 2.19 | 2.45 | 3.06 | 2.75 |
| P<2.2×10-5b | 3.63 | 3.93 | 4.62 | 4.20 |
| P<3×10-7c | 5.3 | 5.76 | 6.52 | 5.99 |
Suggestive linkage threshold when allele-sharing methods in human sib pairs are used (Lander and Kruglyak 1995).
Significant linkage threshold when allele-sharing methods in human sib pairs are used (Lander and Kruglyak 1995).
Highly significant linkage threshold when allele-sharing methods in human sib pairs are used (Lander and Kruglyak 1995).
Geneticists have traditionally appreciated the use of LOD scores more than that of P values; this is no more obvious than when P values are converted to LOD scores. However, given the plethora of linkage statistics currently available to the genetics community, it is appropriate to reassess the general format that one uses to report linkage results. In conclusion, it is strongly recommended that, to aid in the interpretation of linkage results, the appropriate significance thresholds plus both the LOD score and, most important, the corresponding P value should be reported in all linkage studies.
Footnotes
A Microsoft Excel spreadsheet, for performing easy calculations of P values for the LOD scores described in this review, is available on request from the author.
Electronic-Database Information
The URLs for data in this article are as follows:
- Alphabetical List of Genetic Analysis Software, http://linkage.rockefeller.edu/soft/list.html (for all programs referenced in this review [plus many others])
- ASPEX package, ftp://lahmed.stanford.edu/pub/aspex
- S.A.G.E. (Statistical Analysis for Genetic Epidemiology), release 2.2, http://darwin.mhmc.cwru.edu/pub/sage.html (for S.A.G.E. computer package available from the Department of Epidemiology and Biostatistics, Case Western Reserve University, Cleveland)
- SIBPAIR, ftp://linkage.cpmc.columbia.edu/software/analyze (program for sib-pair analysis on nuclear families)
References
- Barrett S, Beck JC, Bernier R, Bisson E, Braun TA, Casavant TL, Childress D, et al (1999) An autosomal genomic screen for autism. Am J Med Genet 88:609–615 [DOI] [PubMed] [Google Scholar]
- Blackwelder WC, Elston RC (1985) A comparison of sib-pair linkage tests for disease susceptibility loci. Genet Epidemiol 2:85–97 [DOI] [PubMed] [Google Scholar]
- Cordell HJ, Kawaguchi Y, Todd JA, Farrall M (1995) An extension of the maximum LOD score method to X-linked loci. Ann Hum Genet 59:435–449 [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society, Series B 39:1–38 [Google Scholar]
- Durner M, Vieland VJ, Greenberg DA (1999) Further evidence for the increased power of LOD scores compared with nonparametric methods. Am J Hum Genet 64:281–289 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Faraway JJ (1993) Improved sib-pair linkage test for disease susceptibility loci. Genet Epidemiol 10:225–233 [DOI] [PubMed] [Google Scholar]
- Feingold E, Brown PO, Siegmund D (1993) Gaussian models for genetic linkage analysis using complete high-resolution maps of identity by descent. Am J Hum Genet 53:234–251 [PMC free article] [PubMed] [Google Scholar]
- Greenberg DA (1989) Inferring mode of inheritance by comparison of LOD scores. Am J Med Genet 34:480–486 [DOI] [PubMed] [Google Scholar]
- Gudbjartsson DF, Jonasson K, Frigge ML, Kong A (2000) Allegro, a new computer program for multipoint linkage analysis. Nat Genet 25:12–13 [DOI] [PubMed] [Google Scholar]
- Hauser ER, Boehnke M, Guo SW, Risch N (1996) Affected-sib-pair interval mapping and exclusion for complex genetic traits: sampling considerations. Genet Epidemiol 13:117–137 [DOI] [PubMed] [Google Scholar]
- Hodge SE, Abreu PC, Greenberg DA (1997) Magnitude of type I error when single-locus linkage analysis is maximized over models: a simulation study. Am J Hum Genet 60:217–227 [PMC free article] [PubMed] [Google Scholar]
- Holmans P (1993) Asymptotic properties of affected-sib-pair linkage analysis. Am J Hum Genet 52:362–374 [PMC free article] [PubMed] [Google Scholar]
- Holmans P, Clayton D (1995) Efficiency of typing unaffected relatives in an affected-sib-pair linkage study with single-locus and multiple tightly linked markers. Am J Hum Genet 57:1221–1232 [PMC free article] [PubMed] [Google Scholar]
- James JW (1971) Frequency in relatives for an all-or-none trait. Ann Hum Genet 35:47–48 [DOI] [PubMed] [Google Scholar]
- Knapp M (1997) The affected sib pair method for linkage analysis. In: Pawlowitzki IH, Edwards JH, Thompson EA (eds) Genetic mapping of disease genes. Academic Press, London, pp 150–151 [Google Scholar]
- Knapp M, Seuchter SA, Baur MP (1994) Linkage analysis in nuclear families. II. Relationship between affected sib-pair tests and LOD score analysis. Hum Hered 44:44–51 [DOI] [PubMed] [Google Scholar]
- Kong A, Cox NJ (1997) Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61:1179–1188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and non-parametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander ES (1995) Complete multipoint sib-pair analysis of qualitative and quantitative traits. Am J Hum Genet 57:439–454 [PMC free article] [PubMed] [Google Scholar]
- Lander E, Kruglyak L (1995) Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat Genet 11:241–247 [DOI] [PubMed] [Google Scholar]
- Lander ES, Botstein D (1989) Mapping mendelian factors underlying quantitative traits using RFLP linkage maps. Genetics 121:185–199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Green P (1987) Construction of multilocus genetic maps in humans. Proc Natl Acad Sci USA 84:2363–2367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morton NE (1955) Sequential tests for the detection of linkage. Am J Hum Genet 7:277–318 [PMC free article] [PubMed] [Google Scholar]
- Ott J, Hoh J (2000) Statistical approaches to gene mapping. Am J Hum Genet 67:289–294 (in this issue) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Risch N (1990a) Linkage strategies for genetically complex traits. I. Multilocus models. Am J Hum Genet 46:222–228 [PMC free article] [PubMed] [Google Scholar]
- ——— (1990b) Linkage strategies for genetically complex traits. II. The power of affected relative pairs. Am J Hum Genet 46:229–241 [PMC free article] [PubMed] [Google Scholar]
- ——— (1990c) Linkage strategies for genetically complex traits. III. The effect of marker polymorphism on analysis of affected relative pairs. Am J Hum Genet 46:242–253 [PMC free article] [PubMed] [Google Scholar]
- Sham P (1998) Statistics in human genetics. Arnold, London [Google Scholar]
- Terwilliger JD, Ott J (1994) Handbook of human genetic linkage. Johns Hopkins University Press, Baltimore [Google Scholar]
- Vieland VJ, Hodge SE, Greenberg DA (1992) Adequacy of single-locus approximations for linkage analyses of oligogenic traits. Genet Epidemiol 9:45–59 [DOI] [PubMed] [Google Scholar]
- Weeks DE, Lange K (1988) The affected-pedigree-member method of linkage analysis. Am J Hum Genet 42:315–326 [PMC free article] [PubMed] [Google Scholar]
- Whittemore AS (1996) Genome scanning for linkage: an overview. Am J Hum Genet 59:704–716 [PMC free article] [PubMed] [Google Scholar]
- Whittemore AS, Halpern J (1994) A class of tests for linkage using affected pedigree members. Biometrics 50:118–127 [PubMed] [Google Scholar]