The Disequilibrium Maximum-Likelihood–Binomial Test Does Not Replace the Transmission/Disequilibrium Test

To the Editor:

In a previous issue of the Journal, Huang and Jiang (1999) introduced the disequilibrium maximum-likelihood–binomial test (DMLB) for affected-sibship data. The DMLB is supposed to combine the advantages of the mean test (Blackwelder and Elston 1985) and the transmission/disequilibrium test (TDT) (Terwilliger and Ott 1992; Spielman et al. 1993), in that the DMLB performs well when linkage disequilibrium (LD) is low and has power higher than or equal to that of the TDT when the LD ranges from moderate to strong. If this claim was correct, the TDT would be obsolete. In this letter, we show how to compute exact P values and exact critical values for the DMLB (and for the TDT), and we show that, when these exact critical values are used, the DMLB is never significantly more powerful than the TDT when there is complete LD. The opposite is true: the TDT is often significantly more powerful than the DMLB. Even when LD is at 80% of its maximum, the TDT still outperforms the DMLB when the marker- and disease-allele frequencies are identical. The asymptotic approximation used by Huang and Jiang (1999) can be inaccurate. We show that their choice of the critical value for the DMLB (c_DMLB) is often anticonservative—that is, it violates the false-positive rate—whereas their choice of the critical value for the TDT (c_TDT) tends to be overly conservative. The exact critical values depend on the number of heterozygous parents in the sample, and we are making available (contact the corresponding author) an SAS Institute (1990) program that computes exact critical values. Huang and Jiang (1999) introduce DMLB tests for two different cases of hypotheses. For the sake of brevity, we will focus only on the more important two-sided hypothesis, which is relevant when there is no prior knowledge about which marker allele is in LD with the disease. Let us give a brief description of the TDT and the DMLB for families with two affected children. Suppose that there are n₂ heterozygous B₁B₂ parents in the data set. Let n₂₂ denote the number of heterozygous parents who transmitted allele B₁ to both children, let n₂₁ denote the number of heterozygous parents who transmitted B₁ to one child and B₂ to the other child, and let n₂₀ denote the number of heterozygous parents who transmitted B₂ to both children. Then the TDT statistic is given by with an asymptotic χ²₁ distribution under the null hypothesis of no linkage. The score-statistic version of the DMLB is given by

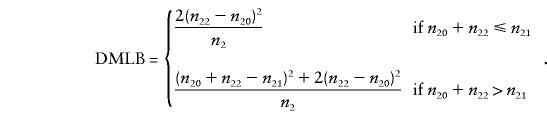Incidentally, we note that 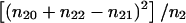equals the mean test for these data. Huang and Jiang (1999) show that, under the null hypothesis of no linkage, the DMLB has the asymptotic distribution .5χ²₁+.5χ²₂. They use this asymptotic distribution to compute the critical value c_DMLB=17.38, corresponding to a false-positive rate of α=.0001. Similarly, under the null hypothesis of no linkage, the TDT has an asymptotic χ²₁ distribution, which can be used to show that, for the same false-positive rate, the critical value of the TDT is given by c_TDT=15.14. These critical values are not ideal, as can be seen from table 1, which lists the exact error rates as a function of the number of heterozygous parents n₂. Fortunately, one does not need to rely on asymptotic approximations, since, under the null hypothesis, one can easily compute exact P values for both tests. However, even if one is not interested in exact P values, one can easily compute the exact critical values that should be used, for families with two affected offspring, to maintain the correct type I error rate. The key observation for these calculations is that, under the null hypothesis, (n₂₂,n₂₁,n₂₀) has a multinomial distribution with parameters n₂ and (p₂,p₁,p₀)=(.25,.5,.25), and the DMLB is a simple function of this low-dimensional distribution. These null distributions can be used to compute the exact critical values for both tests, some of which are listed in table 2. The critical values depend on the sample sizes, but there is no monotonous relationship between the number of heterozygous parents n₂ and the critical values. Since interpolation between the different values of n₂ is difficult, we are making available (contact the corresponding author) an SAS Institute (1990) program that calculates the critical values for both tests.

Table 1.

Exact Error Rates of the DMLB and the TDT Test Statistics When the Critical Values (Corresponding to α=.0001) Proposed by Huang and Jiang (1999) Are Used^[Note]

n2	P(DMLB > 17.38)	P(TDT > 15.14)
30	.0001544	.0000422
50	.0001585	.0000785
100	.0001475	.0000913
300	.0001269	.0001019
500	.0001237	.0000985
700	.0001220	.0001051
1,000	.0001158	.0000902

Note.—The DMLB critical value obviously is anticonservative.

Table 2.

Exact Critical Values for the TDT and the DMLB Corresponding to α, as a Function of n₂

	Exact Values at α =
	.0001		.001		.01		.05
n2	c DMLB	c TDT	c DMLB	c TDT	c DMLB	c TDT	c DMLB	c TDT
30	19.63	15.03	13.43	11.30	8.63	6.70	5.43	4.30
50	18.94	14.46	13.70	10.26	8.38	6.78	5.18	4.02
100	18.17	14.59	13.51	10.59	8.57	6.49	5.29	3.93
300	18.00	15.36	13.12	10.67	8.40	6.83	5.23	3.84

To compare the power of the two tests, we conducted simulation studies for the genetic models studied by Huang and Jiang (1999). We considered four genetic models: additive, dominant, multiplicative, and recessive. Let f₀, f₁, and f₂ be the penetrances of disease genotypes dd, Dd, and DD, respectively, where D is the disease-causing allele. The relative genotypic risks (GRRs) are defined as r₁=f₁/f₀ and r₂=f₂/f₀. Like Huang and Jiang, we considered the following GRR values in the power calculation: (1) for the additive model, r₁=4, r₂=7; (2) for the dominant model, r₁=4, r₂=4; (3) for the multiplicative model, r₁=4, r₂=16; and (4) for the recessive model, r₁=1, r₂=4. We assumed that the biallelic marker and the disease loci are tightly linked (θ=0), and we studied two marker-allele frequencies m (.2 and .5) and three disease-allele frequencies p (.1, .2, and .5). We looked at four different values (1, .80, .50, and .30) of the normalized LD δ_p=Δ/Δ_max, where Δ=P(B₁D)-mp and 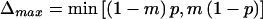. For each genetic model, we determined the approximate number of families N required to yield 80% power for the TDT (Knapp 1999). If N<1,000, then we simulated 100,000 replicates of N families; however, if N>1,000, then each sample was limited to 1,000 families. Both tests were evaluated for the same replicates. For each replicate, we determined the number n₂ of heterozygous parents in the sample and then used it to compute exact critical values for both tests. Since both tests have a discrete distribution, we used a randomized test to reject at an exact false-positive rate of α=.0001.

Table 3 lists the results of our simulation studies. When the marker-allele frequency equals the disease-allele frequency (m=p), the TDT has more power than the DMLB when δ_p⩾.8. Even when δ_p=.5, the DMLB is not consistently more powerful than the TDT.

Table 3.

Comparison of the Power of the DMLB with That of the TDT, When α=.0001

	Power for δp =
	1			.8			.5			.3
Model and p (m)	N	TDT	DMLB	N	TDT	DMLB	N	TDT	DMLB	N	TDT	DMLB
Additive:
.2 (.2)	51	.82	.75	75	.81	.76	173	.80	.80	437	.80	.87
.5 (.5)	95	.81	.73	154	.81	.75	410	.80	.79	1,000	.70	.77
.1 (.2)	68	.82	.78	100	.81	.79	233	.80	.84	596	.80	.92
.5 (.2)	511	.80	.77	772	.80	.79	1,000	.34	.39	1,000	.04	.08
.2 (.5)	123	.81	.77	196	.80	.80	514	.80	.90	1,000	.54	.89
.1 (.5)	177	.80	.80	281	.80	.83	730	.80	.94	1,000	.30	.83
Dominant:
.2 (.2)	71	.81	.76	106	.81	.77	250	.80	.81	642	.80	.88
.5 (.5)	288	.80	.76	461	.80	.77	1,000	.66	.67	1,000	.09	.12
.1 (.2)	82	.81	.78	122	.81	.80	287	.80	.85	741	.80	.93
.5 (.2)	1,000	.55	.52	1,000	.26	.26	1,000	.04	.04	1,000	.00	.01
.2 (.5)	188	.81	.79	300	.80	.82	783	.80	.91	1,000	.26	.66
.1 (.5)	225	.80	.80	356	.80	.85	923	.80	.95	1,000	.19	.69
Multiplicative:
.2 (.2)	25	.84	.78	36	.82	.77	81	.80	.82	201	.80	.91
.5 (.5)	35	.82	.75	61	.82	.79	169	.80	.86	486	.80	.96
.1 (.2)	37	.82	.77	54	.81	.79	123	.81	.86	308	.80	.94
.5 (.2)	235	.80	.82	351	.80	.85	834	.80	.94	1,000	.27	.78
.2 (.5)	50	.82	.78	81	.80	.82	217	.80	.94	612	.80	1.00
.1 (.5)	86	.81	.80	137	.81	.85	357	.80	.96	999	.80	1.00
Recessive:
.2 (.2)	143	.81	.77	211	.80	.78	493	.80	.81	1,000	.62	.72
.5 (.5)	56	.82	.77	92	.81	.79	247	.80	.84	700	.80	.93
.1 (.2)	1,000	.64	.63	1,000	.33	.33	1,000	.05	.05	1,000	.01	.01
.5 (.2)	326	.81	.80	489	.80	.83	1,000	.69	.85	1,000	.13	.42
.2 (.5)	406	.80	.79	636	.80	.82	1,000	.44	.57	1,000	.06	.16
.1 (.5)	1,000	.06	.05	1,000	.02	.02	1,000	.00	.00	1,000	.00	.00

When m≠p and δ_p=1, the TDT is more powerful than the DMLB in all but one case (multiplicative, p=.5, m=.2). However, when δ_p=.8, the DMLB is, “on average,” more powerful than the TDT. When δ_p⩽.5, the DMLB is usually more powerful than the TDT. However, in many cases in which the DMLB is significantly more powerful than the TDT, the required sample sizes are unrealistic (>1,000 families) anyway. Therefore, neither test would be useful in such a setting.

We conclude that, even though tests that can adapt to the degree of LD are a good idea, our simulations have shown that, if the degree of LD is strong (δ_p⩾.80), the DMLB usually is not more powerful than the TDT. For a candidate-gene study in which the typed marker affects the disease risk (i.e., m=p and δ_p=1), the TDT is preferable to the DMLB. In their study, Huang and Jiang (1999) showed that, when the LD is very weak, the mean test has more power than the DMLB. Therefore, the DMLB is most useful when there is moderate LD between marker and disease locus. Unfortunately, in practice, the amount of LD is usually unknown.