The Efficiency of Pooling in the Detection of Rare Mutations

To the Editor:

After citing a variety of uses of pooled testing in genetic studies, Amos et al. (2000) suggested that mutations in individual patients could be detected more efficiently by being tested in pools. A typical mutation-detection protocol requires that many segments of the gene—for example, an amplicon consisting of one or a few close exons—need to be evaluated for detection of a mutation. Thus, even if the mutation has a prevalence of ∼2%, as in the case of BRCA1 or BRCA2 in Ashkenazim (Hartge et al. 1999), the probability that any segment will contain a mutation is much smaller, perhaps on the order of .0005–.005. The use of pools or groups of samples to identify individuals or to estimate the prevalence of such a rare characteristic has been extensively studied in the statistical literature (Dorfman 1943; Sobel and Elashoff 1972; Gastwirth and Hammick 1989; Tu et al. 1995; Brookmeyer 1999). Using the corrected formula (see the erratum by Amos et al. [in this issue]) for the number of runs or tests needed to identify individuals with a mutation, one can fully appreciate the potential of pooling methods. A variant of the grouping procedure is described that in some circumstances leads to greater gains in efficiency when grouped testing is utilized.

The sensitivity of an assay—that is, the probability that a mutation will be detected, given that at least one member of the pool has it—is a potential limiting factor in practice. For screening of individuals to determine their carrier status, the sensitivity should be as close as possible to 100%. For detection of mutations by multiplex single-nucleotide primer extension, 100% sensitivity was achieved in pools of size 10–20 but dropped to 80% in pools of 30 (Krook et al. 1992). When denaturing high-performance liquid chromatography was used to identify BRCA mutations, 100% sensitivity was observed for several amplicons studied in groups of size five to nine (J. Rutter, personal communication). Thus, for the largest pool size for which a mutation detector is 100% sensitive, it is helpful to know the largest mutation prevalence for which pooling is efficient.

Suppose that the prevalence of a mutation in a single unit (exon or amplicon) being studied is π and that n individuals donate samples. For pools of size r, the probability, γ, that at least one member of the pool has a mutation is 1-(1-π)^r. Assume that the test is 100% accurate in classifying a pool as having or not having a mutation. Since Y, the number of runs or tests that need to be done without pooling is n, for any pooling protocol in which the ratio of the expected value (y) of Y:n<1, the strategy saves runs. We denote this ratio by F, for fraction of tests required relative to individual testing; and the efficiency of a pooling method is 1-F, the fraction of tests saved. When the classical single-stage pooling method (Dorfman 1943), which retests, one at a time, the individuals in a positive pool, is used, the expected number of runs needed to completely identify all the mutations in the segment under study in the sample of n individuals is

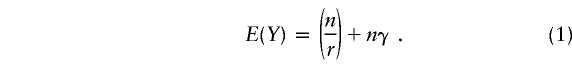The derivation follows. The probability that a pool contains a mutation, which implies that it will test positive, is γ. Since all r individuals in the pool will be tested, a positive pool receives a total of r+1 tests. The probability that a pool is negative is (1-γ). Those pools are classified with one test, so the expected number of tests per pool is (r+1)γ+(1-γ)=1+γr. Since there are  n/r pools, the expected number of tests is given by equation (1). Note that the prevalence, π, enters into equation (1) because it determines the probability, γ, that a pool is positive.

Amos et al. (2000) also considered the situation in which there is a probability β, of a false-positive result in a pool—that is, 1-β is the specificity of the mutation-detection process while the sensitivity remains perfect. The same reasoning that led to equation (1) shows that the expected number, y, of runs or tests is given by

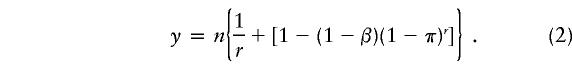From equations (1) and (2), we can calculate the range of values of π for which the ratio of the expected number, y, of tests or runs (Y) to the total sample size, n, is <1, which implies that pooling is at least as efficient as individual testing. We also present the largest π value, π_.5, for which  y/n<.5, which indicates that pooling will result in a substantial savings in the expected number of tests. For the case of perfect tests, these values of π₁ and π_.5 are given by

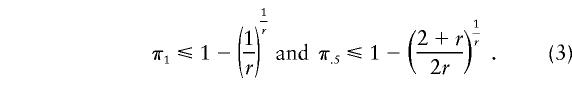When the specificity is 1-β, the equations become

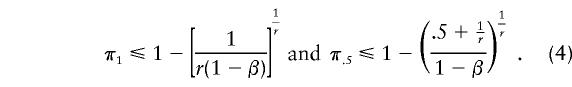In table 1, I present the values of π₁ and π_.5 that are obtained from equations (3) and (4), as a function of r, the pool size. The results for π₁ indicate that pooling in relatively small pools, up to size five or six, can be efficient for values of π⩽.25. Moreover, pools of size ⩽10 can save at least half of the runs, for prevalences ⩽.045, even with a 5% false-positive rate. Indeed, a small lack of specificity does not have a major impact on the range of prevalences for which pooling is useful. For the exons and amplicons occurring in DNA mutation research, in which the prevalence of a mutation at a specific segment being examined is likely to be near .001, pools of 40–100 individual samples would be quite efficient. Of course, this assumes that the sensitivity of the test remains perfect in such samples. Thus, the major limitation in the use of pooling techniques is the maximum size of the group for which the sensitivity of the test is essentially 1.

Table 1.

Mutation Prevalence for Which Pooling Is Efficient, as a Function of Pool Size

	Largest Prevalence for Which  y/n Is
	<1		<.5
Pool Size	β=0	β=.05	β=0	β=.05
2	.293	.275	Not possible
3	.307	.295	.059	.043
4	.293	.284	.069	.057
5	.275	.268	.069	.059
7	.243	.237	.061	.054
10	.206	.202	.050	.045
12	.187	.184	.044	.040
15	.165	.162	.037	.034
20	.139	.137	.029	.027
25	.121	.119	.024	.022
40	.087	.085	.016	.014
50	.075	.074	.013	.012
75	.056	.055	.009	.008
100	.045	.045	.007	.006

For a specific prevalence π, the optimum pool size is obtained by differentiating equations (1) and (2), respectively, and by setting the derivative to 0. When the test used has perfect sensitivity and specificity, r satisfies

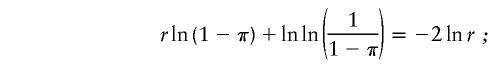when the specificity is 1−β, the optimum pool size r satisfies

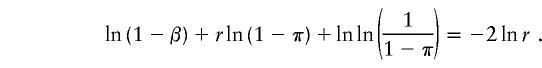The values of r that yield the optimum pool size for a range of prevalences is given in table 2. A small false-positive rate (β=.05) does not have a noticeable impact on the optimal group size but does diminish the efficiency gain in the very-small-prevalence setting when large pools are possible. The results in table 2 indicate that pooling strategies have a greater potential of improving the efficiency of mutation testing than previous results had indicated; for example, when π=.01, the data in table 2 indicate that, for the Dorfman procedure, the optimal pool size is 11 and the expected number of tests is 20%–24% of the number, n, of individuals, depending on whether β=0 or .05.

Table 2.

Optimal Pooling Size and Fraction of Tests Required, Relative to Individual Testing, for Two Pooling Methods

	Optimal Pool Size (% of Tests Required)
	β=0		β=.05
π	Dorfman	One Step	Dorfman	One Step
.2	3 (82.1)	4 (93.1)	3 (84.7)	4 (94.7)
.1	4 (59.4)	5 (60.9)	4 (62.7)	5 (62.6)
.05	5 (42.6)	8 (40.6)	5 (46.5)	7 (41.6)
.01	11 (19.6)	14 (16.0)	11 (24.0)	15 (16.9)
005	15 (13.9)	20 (11.0)	15 (18.5)	21 (11.6)
.001	32 (6.3)	45 (4.7)	33 (11.1)	47 (5.1)
.0005	45 (4.5)	63 (3.3)	46 (9.3)	66 (3.6)
.0001	100 (2.0)	142 (1.4)	103 (6.9)	149 (1.6)

Although a complex multistage sampling protocol may not be appropriate when the optimal pool size is <10 (Amos et al. 2000), a one-step procedure can improve the efficiency of grouping. Consider a pool size r=2m. If the pool tests negative, then all units are mutation free. When a pool tests positive, it is divided into two pools of size m that are tested. For rare mutations, usually only one of the two pools will be positive, so only m further tests are needed. A simple upper bound, y_u, for the expected number, y, of tests used by this one-step method is obtained by assuming that, in a positive pool, if there are two or more positive individuals, both half-groups will test positive and all r units will need to be tested. When the false-positive rate for testing a group of size r is β, it is reasonable to assume that the error rate of the test for a pool with half as many individuals ( r/2) is  β/2. Denote the probability that a pool has exactly one positive individual by η=rπ(1-π)^r-1. In this case, the expected number of tests for a pool is

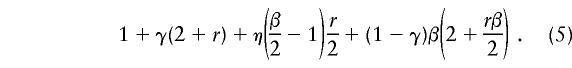The fraction, F, of tests needed relative to individual testing is  1/r times equation (5). When β=0, the upper bound for F for the one-step method becomes

The optimal pool size and fraction of tests with regard to the size, n, of the population screened, as required by the Dorfman and one-step procedures, are given in table 2. When the tests are perfect, the one-step procedure does not yield a substantial increase in efficiency until fairly large pools of a very-low-prevalence mutation can be pooled. The one-step method provides efficiency gains over a larger range of prevalence values and modest pool sizes when there are false-positive pools. This occurs because those pools are truly negative and because there is a very high probability that the two half-pools will be classified correctly by the two tests.

The results indicate that pooling should be quite helpful when a large population is being screened for relatively rare genetic mutations, especially when the prevalence of a mutation in an exon or amplicon is likely to be <.001. As improved technology enables larger pools to be examined (Zarbl et al. 1998), the efficiency of the one-step method should reduce the costs substantially; for example, if the prevalence is .005 and 20 individual samples can be pooled, the number of tests needed is only ∼11% of the number of individuals screened. Greater savings can be achieved, at low prevalences, with multistage (Brookmeyer 1999) or repooling (Munoz-Zanzi et al. 2000) plans.

The formulas for the optimum pool size depend on the prevalence of the mutation in the amplicon assayed. Since this may not be known precisely, one can adopt a two-stage procedure (Hughes-Oliver and Swallow 1994) that changes the pool size on the basis of the estimated prevalence for a partial sample. The results in table 2 can be used to determine the group size for the remaining analyses.

There are several other potential applications of pooling to mutation detection. The methods discussed both here and by Amos et al. (2000) assume perfect sensitivity. In practice, errors occur, so it is useful to use pooling methods to retest a sample of the screened negatives, both to confirm that the sensitivity remains essentially perfect and to ensure that individuals with the mutation are not missed. Such a procedure has been shown to be a cost-effective quality-control method for blood screening (Gastwirth and Johnson 1994). Group testing, without identification of individuals, has also been shown to yield accurate estimates of the prevalence of a rare disease or trait (Gastwirth and Hammick 1989), while preserving the privacy of participants.