Multipoint Genetic Mapping with Uniparental Disomy Data

Abstract

Uniparental disomy (UPD) refers to the presence of two copies of a chromosome from one parent and none from the other parent. In genetic studies of UPDs, many genetic markers are usually used to identify the stage of nondisjunction that leads to UPD and to uncover the associated unusual patterns of recombinations. However, genetic information in such data has not been fully utilized because of the limitations of the existing statistical methods for UPD data. In the present article, we develop a multilocus statistical approach that has the advantages of being able to simultaneously consider all genetic markers for all individuals in the same analysis and to allow general models for the crossover process to incorporate crossover interference. In particular, for a general crossover-process model that assumes only that there exists in each interval at most one crossover, we describe how to use the expectation-maximization algorithm to examine the probability distribution of the recombination events underlying meioses leading to UPD. We can also use this flexible approach to create genetic maps based on UPD data and to inspect recombination differences between meioses exhibiting UPD and normal meioses. The proposed method has been implemented in a computer program, and we illustrate the proposed approach through its application to a set of UPD15 data.

Introduction

Nondisjunction is defined as the appearance of two copies of a single chromosome in a gamete, and it is the result of the failure of the chromosomes to separate during meiosis. Chromosome nondisjunction may lead to uniparental disomy (UPD), in which the chromosome number in an individual is normal but both homologues of a chromosome pair have originated from a single parent (Engel 1980). Genetic conditions that are often associated with UPD15 are Prader-Willi syndrome and Angelman syndrome. Chromosome nondisjunction may also lead to trisomy, the most commonly identified chromosome abnormality in humans (Hassold and Jacobs 1984). In particular, trisomy 21 is responsible for >95% of cases of Down syndrome (Fryns 1987).

Recent studies of trisomy 21 have shown that both altered levels of recombination and altered exchange patterns are associated with maternal nondisjunction (Lamb et al. 1996, 1997a). Analyzing UPD15 cases, Robinson et al. (1998) found a 26% reduction in genetic length, compared with that in controls. Although these studies have revealed that the recombination patterns among meioses leading to nondisjunction may be different from those among normal meioses, information in the collected data has not been fully utilized by the existing methods as reviewed in the following paragraph. The objective of the present article is to develop a general statistical approach that overcomes the limitations of the existing methods in the analysis of UPD data.

Genetic-mapping methods for nondisjoined chromosomes have been discussed by Shahar and Morton (1986), Chakravarti and Slaugenhaupt (1987), Chakravarti et al. (1989), Feingold et al. (2000), and other researchers. In most studies, genetic-map construction is divided into two steps. In the first step, by treating the more proximal marker as a pseudocentromere, pairwise LOD scores are calculated for each pair of markers, via the observed patterns of nonreduction (heterozygous genotype) and reduction (homozygous genotype) of markers along the nondisjoined chromosome pair. In the second step, these pairwise LOD scores are compiled to derive an estimated genetic map. The limitations of such methods are as follows: (1) instead of using multilocus information jointly, they use markers only sequentially, and thus many informative cases are discarded in the pairwise analysis, because not all the markers are typed and informative; (2) the procedures used to compile pairwise LOD scores are ad hoc, and the direction of bias is difficult to evaluate; (3) crossover interference can be accounted for only at the stage at which pairwise distances are combined, although crossover interference has been observed in humans (e.g. Hultén 1974, Broman and Weber 2000); and (4) joint recombination patterns across a set of intervals cannot be recovered from such analysis. Chakravarti et al. (1989) proposed two approaches for multilocus analysis. One approach is to assume that there are, at most, three chiasmata across the region under study, with, at most, one chiasma in a given marker interval. The other approach is to treat the proximal marker as a pseudocentromere relative to the distal marker. The first approach is not applicable either to chromosomes likely to have more than three chiasmata or for studies involving large marker intervals, whereas the second approach implicitly assumes the absence of chiasma interference. More recently, Feingold et al. (2000) have derived multipoint likelihoods for trisomy data under the assumption of no crossover interference. However, the genetic-distance estimates derived by their approach may be biased, because crossover interference does seem to exist during normal human meiosis (Broman and Weber 2000). Given the limitations of the existing methods, our goal in the present article is to develop a multilocus statistical approach that can simultaneously consider all genetic markers for all individuals in the same analysis and that can allow general models for the crossover process to incorporate crossover interference.

The basic idea of our approach is to relate UPD to ordered tetrads, in which four meiotic products can be recovered together and the asci are produced in a linear order corresponding to the meiotic divisions—for example, in Neurospora crassa. Zhao and Speed (1998a) have developed a general framework for the ordering and mapping of genetic markers by using multilocus ordered tetrads. Assuming that phases are known in the parents, Zhao and Speed (1998b) also have derived the relationships between multilocus probabilities for nondisjunction data in experimental organisms—for example, attached X chromosomes in Drosophila (Beadle and Emerson 1935) and half-tetrads in alfalfa (Tavoletti et al. 1996)—and multilocus ordered tetrad probabilities. These relationships can be used to construct genetic maps on the basis of nondisjunction data for any crossover-process model. However, the phases in the parents are generally unknown for UPD, so the results reported by Zhao and Speed (1998b) are not readily applicable to UPD. In the present article, the UPD problem is solved by extending the results reported by Zhao and Speed.

The rest of the present article is structured as follows. In the Methods section, we first derive general relationships between multilocus UPD probabilities and ordered tetrad probabilities. We then discuss how these relationships can be used to make statistical inferences about genetic parameters—for example, genetic distances—related to the crossover process during meiosis leading to UPD. The advantages of our approach are that it can include untyped and uninformative markers in the analysis and that it also can incorporate crossover interference. In particular, we focus on a general crossover-process model in which the only assumption is that there is, at most, one chiasma within each marker interval. We describe how, in this model, genetic parameters can be estimated on the basis of UPD data, by use of the expectation-maximization (EM) algorithm (Dempster et al. 1977). In the Results section, we apply our method to a UPD15 data set. Finally, in the Discussion section, we conclude with comments on our methods and related issues.

Methods

Notation for Multilocus Ordered Tetrad Data

In the present article, markers are denoted by script letters. For example, we use “𝒜” to denote a genetic marker. Alleles are denoted by italic letters. For example, A and a denote two alleles of marker 𝒜. We use [X,Y;Z,W] to denote the observed marker configuration for an ordered tetrad, where X and Y are attached to one centromere and Z and W are attached to the other centromere; for example, [AB,Ab;aB,ab] represents an ordered tetrad with two strands, one each carrying AB and Ab, attached to one centromere and with two strands, one each carrying aB and ab, attached to the other centromere. The centromere is denoted by “CEN.” For patterns between a pair of markers, we use P to denote the parental ditype, where all four strands retain the parental type, T to denote the tetratype, where two of the four strands show recombination, and N to denote the nonparental ditype, where all four strands are recombinants. Throughout the article, we assume the absence of chromatid interference (Zhao et al. 1995b).

For a genetic marker 𝒜 segregating with two alleles A and a, there are six distinguishable patterns for ordered tetrads: I,[A,A;a,a]; II, [A,a;A,a]; III, [A,a;a,A]; IV, [a,A;A,a]; V,[a,A;a,A]; and VI, [a,a;A,A]. Patterns I and VI are called the “first-division segregation”(FDS) pattern, and patterns II–V are called the “second-division segregation”(SDS) pattern (Griffiths et al. 1996). It is easy to see that marker 𝒜 has the FDS pattern when there is no chiasma between CEN and 𝒜 and that it has the SDS pattern when there is exactly one chiasma between CEN and 𝒜 . In general, if there are k chiasmata between the centromere and 𝒜, then the probability that 𝒜 has the FDS pattern is  2/3[ 1/2+(- 1/2)^k] (Mather 1935). Note that marker 𝒜 having the FDS pattern corresponds to pattern P or N between CEN and 𝒜 and that marker 𝒜 having the SDS pattern corresponds to pattern T between CEN and 𝒜.

For ordered tetrads, we distinguish 2×3^n-1 states for n markers in the order CEN-𝒜₁-𝒜₂-…-𝒜_n. Each of these 2×3^n-1 states is represented by J_n=(j₁,j₂,...,j_n), where j₁=0 or 1 corresponds, respectively, to FDS or SDS at 𝒜₁ and where j_r=0, 1, or 2 corresponds, respectively, to P, T, or N between 𝒜_r-1 and 𝒜_r, for r=2,...,n. We denote the probability of ordered tetrad state J_n by p_Jn.

Notation for Multilocus UPD Data

Consider n markers with each marker 𝒜_r, r=1,...,n, being heterozygous with alleles A_r and a_r in the parent undergoing nondisjunction. There can be 0, 1, or 2 copies of allele A_r observed at marker 𝒜_r on the two nondisjoined chromosomes. When the phases in the parent are unknown, we distinguish 2ⁿ distinct states for joint genotypes on the two nondisjoined chromosomes. Each of these states is denoted by I_n=(i₁,i₂,...,i_n), where i_k=0 or 1 corresponds to the kth marker being homozygous or heterozygous. The probability for each pattern I_n is denoted by u_In. Note that, throughout the present article, we use J to denote an ordered tetrad state and I to denote a UPD state. Their corresponding probabilities are denoted by p_J and u_I, respectively.

General Relationships between Multilocus-UPD Probabilities and Ordered-Tetrad Probabilities

Having introduced the notation both for the states of ordered tetrads and UPD and for their probabilities, we now establish general relationships between u_I and p_J. These relationships are important for the following reasons. When a crossover-process model— such as the Poisson model or the more general χ² model (Zhao et al. 1995a)—is specified, ordered-tetrad probabilities can be derived more easily than can UPD probabilities. Therefore, these relationships will allow us to express the likelihood of any UPD state, by using ordered-tetrad probabilities p_J, so that we can use the UPD data to make statistical inferences about the parameters involved in the crossover-process model, such as genetic distances among the markers. The model on which we will focus in the present article is a very general one, which assumes only that, during meiosis, there is, at most, one chiasma in each marker interval. Under this model, joint recombination events during meiosis could be directly inferred if tetrad data were available. This is because (a) the observed parental ditype between two markers corresponds to no chiasmata in this marker interval and (b) the observed tetratype between two markers must be the result of a single chiasma within this interval; however, the presence of only two chromatids in the UPD data prevents us from making such simple inference. Nonetheless, with the general relationships established in the following discussion, we can use UPD data to make statistical inferences about ordered-tetrad probabilities, for any joint-tetrad pattern, at the four-strand stage during meiosis.

Before we establish the general relationships between the p_J and the u_I for an arbitrary number of markers, we will first discuss the relationships involving a single marker and two markers, respectively. In the case of a single marker 𝒜 being heterozygous in the parent, recall that the two states at 𝒜 for UPD data are denoted by I₁=(i₁), where i₁=0 corresponds to marker 𝒜 being homozygous (genotype AA or aa) and where i₁=1 corresponds to 𝒜 being heterozygous (genotype Aa). For ordered tetrads, the two states at 𝒜 are denoted by J₁=(j₁), where j₁=0 corresponds to the FDS pattern at 𝒜 and where j₁=1 corresponds to the SDS pattern at 𝒜. We need to relate the UPD probabilities (u₀,u₁) to the ordered-tetrad probabilities (p₀,p₁).

Meiotic nondisjunction events are classified as meiosis I (MI) nondisjunction if the two copies of the same chromosome are homologous and are classified as meiosis II (MII) nondisjunction if the two copies are sister chromatids (Orr-Weaver 1996). For MI nondisjunction, the FDS pattern at 𝒜 results in UPD being heterozygous at 𝒜, and the SDS pattern at 𝒜 produces a homozygous or heterozygous marker genotype, with equal chance. Therefore, for MI nondisjunction,

For MII nondisjunction, the FDS pattern at 𝒜 always results in a homozygous genotype at 𝒜, whereas the SDS pattern at 𝒜 always results in a heterozygous genotype at 𝒜. Therefore, for MII nondisjunction,

To extend these relationships to two or more markers, we first consider MI nondisjunction. For two markers in the order CEN-𝒜-ℬ, recall that we distinguish four states for the UPD data denoted by I₂=(i₁,i₂), where i_k=0 or 1 corresponds to the kth marker being homozygous or heterozygous, and we distinguish six states for ordered tetrads denoted by J₂=(j₁,j₂), where j₁=0 or 1 corresponds to the FDS or SDS pattern at 𝒜, and j₂=0, 1, or 2 corresponds to P, T, or N between 𝒜 and ℬ. We can show that the relationships between u_I2, the UPD probabilities, and p_J2, the ordered-tetrad probabilities, are

These relationships can be established by examination of the nondisjunction outcomes for each ordered-tetrad pattern. For example, when the notation introduced for ordered tetrads is used, the ordered tetrads [Ab,aB;AB,ab] have equal chances of producing one of the following four UPD patterns: (AA,Bb), (Aa,bb), (Aa,BB), and (aa,Bb). This ordered tetrad corresponds to the ordered-tetrad state I₂=(i₀,i₁)=(1,1), and the four UPD patterns correspond to the UPD states J₂=(j₀,j₁)=(0,1), (1,0), (1,0), and (0,1). Therefore, [Ab,aB;AB,ab] gives rise to UPD states (0,1) and (1,1), with equal chance. Other patterns of ordered tetrads with state (1,1)—for example, [AB,aB;Ab,ab], also give rise UPD states (0,1) and (1,1), with equal probability. When we write these equations in matrix form, we have

In the general case of n markers, we show, in Appendix A, that the multilocus UPD probabilities u_In can be expressed in terms of the multilocus ordered-tetrad probabilities p_Jn, as

The coefficients a[I_n,J_n] in this expression can be obtained in an iterative way, as follows. Write a[I_n,J_n] into a matrix such that the columns are labeled by J_n=(j₁,j₂,...,j_n) in lexicographical order and such that the rows are labeled by I_n=(i₁,i₂,...,i_n) in lexicographical order. Let

then, the matrix A_r+1=(a[I_r+1,J_r+1])_2^r+1×3^r+1 can be obtained by replacing each a[I_r,J_r] in A_r by the 2×3 matrix a[I_r,J_r]E_ir. This establishes the general relationships between multilocus UPD probabilities u_In and multilocus ordered-tetrad probabilities p_Jn, for MI nondisjunction.

For MII nondisjunction, we can similarly derive general relationships between the multilocus UPD probabilities u_In and the multilocus ordered-tetrad probabilities p_Jn:

To find the values for each b[I_n,J_n], write b[I_n,J_n] into a matrix such that the columns are labeled by J_n=(j₁,j₂,...,j_n) in lexicographical order and such that the rows are labeled by I_n=(i₁,i₂,...,i_n) in lexicographical order. Let

Using a proof similar to that which we give, in Appendix A, for MI nondisjunction, we can show that the matrix B_r+1=(b[I_r+1,J_r+1])_2^r+1×3^r+1 can be obtained by replacing each b[I_r,J_r] in B_r by the 2×3 matrix b[I_r,J_r]E_ir, where the E_ir matrices are the same as those used the MI nondisjunction case.

A General Model for the Crossover Process

The general relationships discussed above allow us to incorporate any crossover-process model to analyze UPD data, provided that we can evaluate multilocus ordered-tetrad probabilities. To make the underlying chiasma process as general as possible, here we focus on a crossover process model that has only one restriction on the joint recombination probabilities: across the set of markers being studied, there is, at most, one chiasma in each marker interval. This assumption is likely to be true if the markers are sufficiently close to each other. Under this model, there are only two possible types between two markers for an ordered tetrad: parental ditype (P) and tetratype (T). These two types correspond to exactly 0 and 1 chiasma between two markers.

For this model, we distinguish 2ⁿ distinct states for ordered tetrads involving n markers. Each of these 2ⁿ states can be represented as J_n=(j₁,j₂,...,j_n), where j_r=0 or 1 corresponds to P or T between 𝒜_r-1 and 𝒜_r (𝒜₀=CEN), for r=1,...,n. The probability of state J_n is also denoted by p_Jn, as for the general case. The model parameters for this model are the joint ordered-tetrad probabilities, excluding the possibility of nonparental ditype in any marker interval. Under this model, the general relationships between UPD probabilities and ordered-tetrad probabilities in equation (1) reduce to

for MI nondisjunction. The coefficients c[I_n,J_n] can be obtained in an iterative way. Write c[I_n,J_n] into a matrix such that the columns are labeled by J_n in lexicographical order and such that the rows are labeled by I_n in lexicographical order. Let

The matrix C_r+1=(c[I_r+1,J_r+1])_2^r+1×2^r+1 can be obtained by replacing each c[I_r,J_r] in C_r by the 2×2 matrix c[I_r,J_r]G_ir. It is easy to see that the difference between this special case and the general case discussed above is that, in both E₀ and E₁, we delete the last column, to obtain G₀ and G₁.

For MII nondisjunction, we can similarly derive the relationships between the multilocus UPD probabilities u_In and the multilocus ordered-tetrad probabilities p_Jn, as

Write d[I_n,J_n] into a matrix such that the columns are labeled by J_n in lexicographical order and such that the rows are labeled by I_n in lexicographical order. Let

The matrix D_r+1=(d[I_r+1,J_r+1])_2^r+1×2^r+1 can be obtained by replacing each d[I_r,J_r] in D_r by the 2×2 matrix d[I_r,J_r]G_ir.

UPD-Data Representation

For UPD data, many markers may be untyped or uninformative. At any given locus, in addition to using R (reduced) and N (nonreduced) to denote homozygous genotype and heterozygous genotype for the two chromosomes when the marker is heterozygous in the parent, we use M to denote an untyped or an uninformative marker. Therefore, each UPD individual can be represented as a character string using R, N, and M—such as “…NRNMN….”

Maximum-Likelihood Estimates of Multilocus Ordered-Tetrad Probabilities p_Jn If There Is at Most One Chiasma within Each Marker Interval

Assume that we have collected a sample of individuals with UPD, each of whom is typed at some of the n genetic markers. For the model discussed above, we can use the EM algorithm to estimate the model parameters, which are the multilocus ordered-tetrad probabilities p_Jn. For either MI- or MII-error cases, we start the EM algorithm with initial estimates of the multilocus ordered-tetrad probabilities p⁰_Jn. The E-step computes the expected number of each possible ordered-tetrad state J_n conditional on the observed UPD data and the initial values p⁰_Jn. The M-step then maximizes the likelihood of this “expected” data set and thus generates updated estimates of p_Jn. These new estimates are fed back into the E-step, and the algorithm iterates until the estimates converge. Details concerning the E-step and the M-step are described in Appendix B.

Once we obtain the maximum-likelihood estimates of ordered-tetrad probabilities p_Jn, we can use these parameter estimates to examine different aspects of the crossover process leading to nondisjunction. The estimate of p_Jn is denoted by . We use the three-marker case (the three markers are in the order CEN-𝒜₁-𝒜₂-𝒜 ₃) as an example to illustrate the principles. First, the estimated probability for each ordered-tetrad state, with either parental ditype or tetratype in each marker interval, is the estimated probability, over the chromosomal segment studied, of the joint recombination events, with parental ditype corresponding to no chiasmata, and with tetratype corresponding to one chiasma, in each marker interval; for example, the joint probability that there is one chiasma between CEN and 𝒜₁, no chiasmata between 𝒜₁ and 𝒜₂, and one chiasma between 𝒜₂ and 𝒜₃ can be estimated by . Second, we can estimate the frequency, across the whole chromosomal segment studied, of having a given number of chiasmata; for example, the estimated probability of having two chiasmata in the whole region is . Third, we can examine the joint distribution of the recombination events in all marker intervals conditional on a given number of chiasmata in the whole region. For example, the probability that the two chiasmata occur in the CEN–𝒜₁ and the 𝒜₂–𝒜₃ intervals conditional on having two chiasmata in the whole region can be estimated by 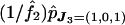. Last, we can estimate the genetic distance between each pair of consecutive markers, 𝒜_r and 𝒜_r+1, by .

We employ the bootstrap method to approximate the uncertainties in the parameter estimates discussed above (Efron and Tibshirani 1993). For the bootstrap method, we first simulate B sets of UPD data, each having the same sample size as that of the observed sample. In the simulations, we first calculate the estimated probability of each UPD state I_n, 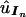, via the estimated ordered-tetrad probabilities and the general relationships established in equation (2) or equation (3). Then each simulated observation is a random sample from a multinomial distribution with all possible UPD states as outcomes and with their associated probabilities being 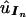. We can estimate the parameters of interest from each simulated data set in exactly the same way as we estimate these parameters from the observed data. If genetic distances are the parameters of interest, we use 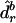to denote the estimated genetic distance in the rth marker interval for the bth simulated data set. From the B bootstrap samples, the standard error (SE) for the estimated genetic distance in the rth marker interval, 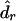, can be estimated by

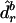where is the mean of the values.

Results

Maternal UPD15 is found in ∼25% of patients with Prader-Willi syndrome (Nicholls et al. 1989; Robinson et al. 1991). It has been found that the nondisjunction event leading to UPD15 is predominantly due to a maternal MI segregation error and that there is a maternal age effect (Robinson et al. 1998). In this section, we apply the methods discussed in the previous section, to analyze one UPD15 data set consisting of 81 cases of UPD15. The data set analyzed here represents only a subset of the 115 cases analyzed by Robinson et al. (1998), because of the exclusion both of trisomy cases and of some UPD cases that were typed entirely outside the Robinson lab and that therefore included a largely different set of markers.

Because markers for the centromere of chromosome 15 were not available, we used markers D15S541, D15S542, and D15S543 to infer the meiotic stage of origin. These markers are the markers most proximal to the centromere. Because there is no known crossing-over between them, as is also the case in the study by Robinson et al. (1998), we treated them as one marker and were able to determine meiotic stage of origin for each case. Of the 81 cases of UPD, 12 were identified as being due to MII errors. In our analysis, we considered 10 markers spanning the interval CEN–D15S87 that were in the order CEN-GABRB3-D15S24-ACTC-CYP19-D15S98-D15S108-D15S131-D15S114-D15S100-D15S87. In light of the presence of many untyped and uninformative markers in the data set, we chose these markers because they had the lowest amount of missing information. The overall percentage of untyped and uninformative markers for these 10 markers, across all individuals, was 44%.

Because there were 12 cases due to MII errors, we present here only our results on UPDs that were due to MI errors. For the 69 MI cases, we estimated the ordered-tetrad probabilities p_Jn by using this 10-marker data set. As discussed in the Methods section, the 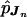can be used to examine different aspects of the recombination process leading to UPD. In table 1, we summarize the estimated genetic distances based on the 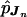values among the 10 markers. The SEs were estimated on the basis of the bootstrap method, with 1,000 simulated samples. The estimated total genetic distance from CEN to D15S87 was 101.4 cM, with a SE of 11.5 cM. We also estimated the SEs by using the jackknife method, and the results were very similar (data not shown). Using sequential pairwise analyses, Robinson et al. (1998) estimated tetratype frequency and genetic distance for each interval, on the basis of the number of observed exchanges (transitions from nonreduced to reduced markers, or vice versa). The total genetic distance between CEN and D15S87, on the basis of MI nondisjunction events, was estimated by summation of the estimated lengths from all intervals. Although Robinson et al. (1998) used this different method to analyze 97 cases with MI errors (a superset of the 69 cases analyzed here), their estimate of the total genetic length, 95.8 cM, was similar to our estimate, 101.4 cM.

Table 1.

Estimated Genetic Distances on the Basis of 10-Marker UPD Data, for 69 Cases Due to MI Error

	Genetic Distance ± SEa(cM)
Marker	MI UPD	Soton Map
CEN	…	…
GABRB3	.0 ± .0	3.8
D15S24	3.3 ± 1.9	11.9
ACTC	4.8 ± 2.5	12.5
CYP19	17.3 ± 4.6	17.4
D15S98	10.1 ± 4.4	15.9
D15S108	7.8 ± 4.1	11.5
D15S131	19.3 ± 4.5	19.4
D15S114	5.0 ± 3.1	4.2
D15S100	16.7 ± 5.5	38.4
D15S87	17.1 ± 5.2	13.0
Total	101.4 ± 11.5	148.1b

^aSEs are estimated from 1,000 bootstrap samples. The “Soton Map” entries, which are shown for purposes of comparisons, are estimated from normal female meioses compiled by The Genome Database.

^bBecause of rounding error, entries do not sum to exactly the total shown.

In table 1, we also compare the estimated genetic distances based on UPD data, using these 10 markers with the female genetic map derived from normal meioses maintained at The Genetic Location Database. There is a reduction in genetic distance for some intervals, and the total genetic distance based on UPD data is almost one-third shorter than that based on normal meioses. The largest reduction occurs in the D15S100–D15S87 interval. To allow formal statistical testing using the approach developed in the present article, we need to apply the same statistical model to standard pedigree data from normal meioses—for example, data from CEPH pedigrees. Because such implementations and comparisons are beyond the scope of the present article, which focuses on the developments of a general model for UPD data from nuclear families, we will address this issue in a separate report. Nevertheless, by using the genetic distance estimates and their SEs, we can see that the reductions in three marker intervals—D15S24–ACTC, ACTC–CYP19, and D15S100–D15S87are likely to be significant. If we use alternative models that use only genetic distances to derive all multilocus UPD-pattern probabilities—for example, the χ² model (Zhao et al. 1995a)—rigorous statistical tests can be performed by letting the genetic distances equal the values estimated on the basis of the normal meioses, under the null hypothesis, and allowing them to vary freely, under the alternative hypothesis. Likelihood-ratio tests can thus be performed to test whether the genetic distances significantly differ, between meioses leading to UPD and normal meioses.

As mentioned in the Methods section, in addition to genetic distances, we can also study the probability distribution of recombination patterns by using the estimated ordered-tetrad probabilities. We first estimated the distribution of the number of chiasmata in the UPD data. With the 10 markers used in the analysis, the estimated proportions of tetrads with 0, 1, 2, 3, 4, 5, and 6 chiasmata were 14.5%, 18.8%, 21%, 41.6%, 3.3%, 0.7%, and 0.1%, respectively. At a frequency of 41.6%, tetrads with three chiasmata represented the most common class. This result agrees with the estimate by Robinson et al. (1998), who estimated the proportion of tetrads with three chiasmata as being 48%. For other numbers of chiasmata, the estimates of tetrads with 0, 1, 2, and 4 chiasmata were 21%, 22%, 0%, and 9%, respectively. Although the two sets of estimates generally agree, differences in the methodology cause discrepancies to occur; the largest is for the class of tetrads with 2 chiasmata, for which Robinson et al. reported 0% and we report 21%. Because our estimates were based on a very general and comprehensive framework, our approach may provide better estimates than those provided by the approach adopted by Robinson et al. (1998).

One major advantage of our approach is that it allows us to examine the joint distribution of recombination events along the chromosome conditional on a given number of chiasmata. In table 2, we summarize such conditional distributions of the chiasmata among the 10 intervals. When there was a single chiasma in the whole region, it occurred only within the last two marker intervals. For the 2-chiasmata case, the mode of the first chiasma (>50%) was in the fifth marker interval, whose genetic length was estimated at only 10 cM, and the second chiasma was distributed with approximately the same proportion in the sixth, seventh, and the ninth interval. In contrast to the 1-chiasma case, in which the last interval had >30% of the chiasmata, only 8% of the tetrads had 1 chiasma in the last interval when 2 chiasmata occurred on the tetrads. When there were 3 chiasmata, the most common pattern was that the first chiasma occurred in the fourth interval, the second chiasma occurred in the seventh interval, and the third chiasma occurred in the last interval. The exchange patterns conditional on a total of four chiasmata in the region were much less reliable because they were derived from only 3.3% of the total cases.

Table 2.

Conditional Exchange Patterns for Chiasmata When Total Number of Chiasmata on Tetrads Is k = 0, 1, 2, 3, and 4

	1	2	3	4	5	6	7	8	9	10
	Frequency, Conditional on k, in Interval
k (distribution):
0 (.145)	…	…	…	…	…	…	…	…	…	…
1 (.188)	.00	.00	.00	.00	.00	.00	.00	.00	.68	.32
2 (.210):
First	.00	.19	.01	.08	.56	.07	.00	.04	.05	.00
Second	.00	.00	.00	.00	.05	.37	.26	.00	.25	.08
3 (.416):
First	.00	.05	.20	.62	.09	.04	.00	.00	.00	.00
Second	.00	.00	.00	.13	.05	.04	.72	.04	.03	.00
Third	.00	.00	.00	.00	.00	.01	.01	.12	.26	.59
4 (.033):
First	.00	.12	.03	.27	.06	.52	.00	.00	.00	.00
Second	.00	.00	.09	.06	.15	.06	.67	.00	.00	.00
Third	.00	.00	.00	.03	.09	.06	.06	.64	.09	.00
Fourth	.00	.00	.00	.00	.00	.03	.00	.03	.48	.45
	Map Distance(cM)
Total	.0	3.3	4.8	17.3	10.1	7.8	19.3	5.0	16.7	17.1

Discussion

Recent studies of nondisjunction data on humans have revealed that both altered levels of recombination and altered exchange patterns may be associated with nondisjunction, at both MI and MII (Lamb et al. 1996, 1997a; Robinson et al. 1998). However, these studies have not been able to fully utilize the genetic information in the collected data in their analysis, because of the limitations in the existing methods. To address this problem, in the present article we have developed a general framework within which to analyze UPD data. Our multilocus approach is based on the relationships that we have established between multilocus UPD probabilities and multilocus ordered-tetrad probabilities. All genetic markers, including untyped and uninformative markers, are simultaneously utilized to study the recombination patterns leading to UPD.

In principle, our approach allows us to incorporate any crossover-process model, to analyze multilocus UPD data. In the present article, we have focused on a very general model, which assumes only that there is, at most, one chiasma in each marker interval on the tetrads. For this particular model, we have implemented an EM algorithm to estimate multilocus ordered-tetrad probabilities on the basis of the observed UPD data, in a computer program that will be made available at our Web site (Hongyu Zhao's Lab of Statistical Genetics). Provided that there are many markers available, so that the chance of having more than one chiasma in a particular interval is small, this model will capture most of the recombination events. This assumption is likely to hold for most of the marker intervals in the UPD data analyzed in the Results section, although it would be more helpful to analyze additional markers in the four intervals with the largest genetic distance—that is, intervals ACTC–CYP19, D15S108–D15S131, D15S114–D15S100, and D15S100–D15S87. We have also illustrated how to use the estimated ordered-tetrad probabilities to estimate genetic distances among markers, how to estimate the distribution of the number of chiasmata in the chromosomal region under study, and, given a certain number of chiasmata in the region, how to estimate the joint conditional distribution of recombination events.

Weinstein (1936) presented methods for inferring, from the observed recombination patterns, the frequency of tetrads of various ranks (i.e., zero, single, and multiple exchanges) in a population of Drosophila. On the basis of the methods of Weinstein (1936), Lamb et al. (1997b) estimated chiasma distributions for the human female chromosome 21. In another study, Lamb et al. (1997a) applied the principles of Weinstein’s methods to the analysis of trisomy data. They first divided the whole chromosome into intervals that were long enough to have a few informative markers in each interval and short enough to have only 1 chiasma. Then they scored either recombination or its absence across each interval, using observed marker information. When there was ambiguity, a single recombination event was split between the two adjacent intervals. Compared with the method discussed by Lamb et al. (1997b), the advantages of our approach are that (1) we directly work on the UPD data themselves, without making inference about whether a recombination event has occurred in a marker interval and (2) missing data are incorporated in a more sophisticated way, through the application of the EM algorithm. The same approach can be applied to the analysis of ovarian teratomas (Ott et al. 1976). With some modifications, this method has been extended to the analysis of trisomy data on humans (J. Li and H. Zhao, unpublished results). In the case of the Poisson model for the crossover process, results from our extended approach were identical to those discussed by Feingold et al. (2000).

In our classification of UPDs as being due to either MI errors or MII errors, we used D15S541, D15S542, and D15S543 to infer the meiotic stage of nondisjunction origin. By means of this rule, 12 of the 81 cases were identified as being due to MII errors, and 69 cases were identified as being due to MI errors. Because these markers are near but not at the centromere, there may be errors involved in the assignment of origin (Robinson et al. 1993). Therefore, when these markers are used, one would expect some proportions of true MII errors to be misclassified as MI errors, and vice versa. If there is no difference, in exchange patterns, between MI UPD data and MII UPD data, then our estimates of probabilities for exchange patterns are still unbiased. However, the estimated recombination patterns would be biased if significant differences exist between MI nondisjunction events and MII nondisjunction events. These significant differences would be detected by comparison of exchange patterns estimated from “apparent” MI cases and “apparent” MII cases, because the majority of the cases in each group would represent correctly classified cases. In our data set, there were only 12 cases due to MII errors, preventing us from making meaningful comparison. On the other hand, we may treat the “apparent” cases of MI as a mixture of “true” cases of MI and “false” cases of MI. If the mixture proportion is known a priori, then valid statistical inference can still be drawn from such data.

In addition to the general crossover model discussed in the present article, the general relationships between UPD probabilities and ordered-tetrad probabilities allow us to consider any model for the crossover process, as long as ordered-tetrad probabilities can be easily evaluated. The major limitation of such an approach is that the amount of computation increases exponentially with the number of genetic markers analyzed. This may impose potential computational problem if the number of markers is very large. Under the χ² model for the crossover process (Zhao et al. 1995a), hidden Markov models can be used to evaluate the probability of any UPD pattern (H. Zhao and J. Li , unpublished results). The advantage of the hidden-Markov-model approach is that the amount of computation increases linearly with the number of markers, allowing the inclusion of hundreds of markers in the analysis. Another advantage of the χ² model is that many fewer parameters are involved in the model. Therefore, when the crossover-process model is correctly specified, we may obtain more-accurate estimates of genetic parameters of interest and may derive more-powerful tests for hypotheses concerning the recombination process—for example, the hypothesis concerning whether recombination is reduced among meioses leading to nondisjunction. When the χ² model was applied to the same UPD data set, the estimated genetic distances generally agreed with those estimated in the present article, although the estimated distances under the χ² model were larger across a few longer marker intervals. When the likelihood-ratio test was performed to test the null hypothesis of no recombination reduction in UPD meioses, the result was inconclusive, probably because of the small sample size of this data set. Because the mathematical treatments of the UPD data under the χ² model are very different from the approach that we have presented here, the general methods for the χ² model and the results derived from them will be reported in a separate article. Although the χ² model or other models with a few parameters are, in general, computationally attractive, the danger in using them is the possibility that the model assumptions may be incorrect, leading to biased estimates for the genetic parameters of interest. Because the only assumption that underlies the model discussed in the present article is that there is, at most, 1 chiasma in each marker interval, this approach is very likely to yield the most unbiased description of the recombination events during meiosis, if the distances among the markers are sufficiently small. The results from other models can be compared with those from this approach, to assess the goodness of fit of the other models.

Appendix A : Matrix A_n: Proposition and Proof

Proposition A. For MI nondisjunction, the matrix A_n that relates multilocus UPD probabilities and multilocus ordered-tetrad probabilities can be obtained by use of the procedure described in the text.

Proof. When n=1, the FDS pattern yields only the heterozygous pattern (N) and the SDS pattern yields both the heterozygous pattern (N) and the homozygous pattern (R), with the same probability. Therefore,

Suppose that the proposition holds when n=r; that is, u_Ir=Σ_Jra[I_r,J_r]p_Jr, where A_r=(a[I_r,J_r])_2^r×3^r. Consider 𝒜_r+1,

When i_r=0—that is, it is R at 𝒜_r—the tetrad from which the UPD is derived must have the SDS pattern at 𝒜_r. For the parental ditype (j_r+1=0) and the nonparental ditype (j_r+1=2) between 𝒜_r and 𝒜_r+1, it should be homozygous (R) at 𝒜_r+1—that is, i_r+1=0; and, for the tetratype between 𝒜_r and 𝒜_r+1, it should be heterozygous (N) at 𝒜_r+1—that is, i_r+1=1. Therefore,

When i_r=1, then, (1) if j_r+1=0 or 2, then i_r+1=1, and, (2) if j_r+1=1, then i_r+1 has the same probability to be 0 and 1. Therefore,

Note that the lexicographical order is still preserved. This completes the proof of the proposition.

Appendix B : The EM Algorithm for the Maximum-Likelihood Estimates of Multilocus Ordered-Tetrad Probabilities, When It Is Assumed That There Is, at Most, 1 Chiasma within Each Marker Interval

We describe here the EM algorithm for MI nondisjunction data; the algorithm for MII nondisjunction data is similar.

• 1. E-step: Denote the current estimates of ordered-tetrad probabilities by p^c_Jn. Our data reconstruction is performed in two steps: (a) calculate the expected number C_In of each possible UPD state I_n, given the observed data and the current estimates p^c_Jn; and (b) calculate the expected number D_Jn of each possible ordered-tetrad state J_n, on the basis of C_In.

• (a) It is straightforward to calculate the multilocus UPD-state probabilities, I_n, via the relationships established in equation (2). For each individual in the observed sample, if there is no untyped or uninformative marker, this sample case corresponds to a particular UPD pattern I_n=(i₁,i₂,...,i_n), where i_k=0 or 1 for 1⩽k⩽n. So the contribution of this sample case to pattern I_n is 1, and that to all other patterns is 0. If there are h (1⩽h<n) untyped or uninformative markers for an individual, this case corresponds to 2^h different string patterns. Denote the positions of these untyped or uninformative markers by m₁,m₂,...,m_h; the 2^h different UPD patterns can be represented by l_n=(l₁,l₂,...,l_n), where, if k∈{m₁,m₂,...,m_h}, then l_k can take value 0 or 1, and where, if k∉{m₁,m₂,...,m_h}, then l_k takes a fixed value f_k of 0 or 1. Therefore, the contribution of this individual to each of the 2^h different states can be calculated by u_ln/Σ_{lm1,lm2,...,lmh}u_ln, and the contribution of this individual to all other patterns I_n besides these 2^h patterns is 0. If we go through the whole data set in this fashion, we can obtain the expected number C_In for each possible UPD state I_n.
• (b)
  With the relationships between u_In and p_Jn in equation (2), we calculate D_Jn for each ordered-tetrad state, on the basis of the C_In values obtained in step (a), as follows:

  

• 2. M-step: The updated estimates of the multilocus ordered-tetrad probabilities p_Jn are p^new_Jn=D_Jn/S, where S is the sample size. Repeat the E-step and the M-step until convergence is obtained.