Inferring the in vivo looping properties of DNA

Abstract

The free energy of looping DNA by proteins and protein complexes determines to what extent distal DNA sites can affect each other. We inferred its in vivo value through a combined computational–experimental approach for different lengths of the loop and found that, in addition to the intrinsic periodicity of the DNA double helix, the free energy has an oscillatory component of about half the helical period. Moreover, the oscillations have such an amplitude that the effects of regulatory molecules become strongly dependent on their precise DNA positioning and yet easily tunable by their cooperative interactions. These unexpected results can confer to the physical properties of DNA a more prominent role at shaping the properties of gene regulation than previously thought.

The cell is a densely packed dynamic structure made of thousands of different molecular species that orchestrate their interactions to form a functional unit. Such complexity poses a strong barrier for experimentally characterizing the cellular components: not only the properties of the components can change when studied in vitro outside the cell, but also the in vivo probing of the cell can perturb the process under study (1). Here we use computational modeling to obtain the properties of the in vivo unperturbed components at the molecular level from physiological measurements at the cellular level. Explicitly, we infer the in vivo free energies of DNA looping from enzyme production in the lac operon (2).

The formation of DNA loops by the binding of proteins at distal DNA sites plays a fundamental role in many cellular processes, such as transcription, recombination, and replication (3–5). In gene regulation, proteins bound far away from the genes they regulate can be brought to the initiation of transcription region by looping the intervening DNA. The free energy cost of this process determines how easily DNA can loop and therefore the extent to which distal DNA sites can affect each other (5).

In the lac operon, there is a repressor molecule that regulates transcription by binding specifically to DNA sites known as operators and preventing the RNA polymerase from transcribing the genes. DNA looping allows the repressor to bind to two operators simultaneously, leading to an increase in repression of transcription. This increase, characterized by the repression level, can be connected to the free energy of looping DNA by a recent model for transcription regulation by the lac repressor (6). The distance between operators determines the length of the DNA loop and affects the repression level through the changes in the free energy of looping. For interoperator distances from 57.5 to 98.5 bp, Muller et al. (7) systematically varied the distance between two operators in increments of 1 bp and measured the in vivo repression levels under conditions similar to wild type. These physiological measurements of enzyme production in Escherichia coli cell populations allowed us to infer here the in vivo looping properties of DNA with unprecedented accuracy.

Background and Methods

Transcription Regulation in the lac Operon. The lac operon consists of a regulatory domain and three genes required for the uptake and catabolism of lactose. Binding of the lac repressor to the main operator O1 prevents the RNA polymerase from binding to the promoter and transcribing the genes. There are also two auxiliary operators outside the regulatory region, O2 and O3, to which the repressor can bind without preventing transcription. They enhance repression of transcription by increasing the ability of the repressor to bind O1. This effect is mediated by DNA looping, which allows the simultaneous binding of the repressor to the main and one auxiliary operator (2).

To avoid the formation of multiple loops, experiments are typically performed with just the main and one auxiliary operator, as in the case of Muller et al. (7). In such a case, there is transcription when the system is in a state in which

1. none of the operators is occupied, or

2. a repressor is bound to just the auxiliary operator;

and there is no transcription when

• (iii) a repressor is bound to just the main operator,

• (iv) a repressor is bound to both the main and the auxiliary operators by looping the intervening DNA, or

• (v) one repressor is bound to the main operator and another repressor to the auxiliary operator.

In Fig. 1, we illustrate these five possible states for the lac constructs used in the experiments of ref. 7, which consisted of the main operator O1 and just an upstream auxiliary operator, Oid, with the sequence of the ideal operator.

Fig. 1.

Schematic representation of the five possible states for lac repressor binding to two operators for the lac constructs used in the analyzed experiments from Muller et al. (7). The lac Z gene, downstream the main operator, is repressed when the lac repressor (in gray with black contour line) is bound to the main operator (states iii, iv, and v); and unrepressed when the main operator is unoccupied (states i and ii). The thick black line represents the DNA, and the two lac operators are shown as white (auxiliary operator) and highlighted (main operator) boxes. The thick dotted line indicates the different lengths of the spacer DNA between operators.

Repression Level. The repression level, R_loop, is a dimensionless quantity used to measure the extent of repression of a gene. It is defined as the ratio of the unrepressed transcription rate (t_max) to the actual transcription rate (t_act): R_loop = t_max/t_act. The actual transcription rate is the unrepressed transcription rate times the fraction of time that the main operator is free. Therefore, the repression level is the inverse of the probability that the system is in the states i and ii

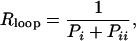where P indicates the probability for the system to be in the state denoted by its subscript.

Statistical Thermodynamics Analysis. Statistical thermodynamics connects the probability P_k of a state k with its standard free energy ΔG_k through 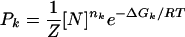, where [N] is the concentration of repressors expressed in moles; n_k is the number of repressors considered in the state k; RT is the gas constant, R, times the absolute temperature, T; and Z = Σ_kP_k is the normalization factor (8).

This relationship between probabilities and free energies leads to

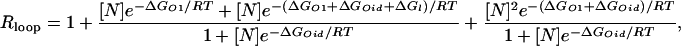where ΔG_O1 and ΔG_Oid are the standard free energies of binding of the repressor to the O1 and Oid operators, respectively, and ΔG_l is the free energy of looping (6).

The free energy of looping is defined from the free energy of the looped state iv, ΔG_iv, which can be decomposed in binding to O1 and Oid and looping contributions: ΔG_iv =ΔG_O1 +ΔG_Oid +ΔG_l (Fig. 2). The free energies of the other states are ΔG_i = 0, ΔG_ii = ΔG_Oid, ΔG_iii = ΔG_O1, and ΔG_v = ΔG_O1 + ΔG_Oid.

Fig. 2.

Cartoon of the lac repressor (in gray with black contour line) bound simultaneously to the main (O1) and one auxiliary operator (Oid, with the sequence of the ideal operator), which are represented by white rectangles. Binding of the repressor to O1 represses the lac Z gene in the experiments (7). The simultaneous binding to O1 and Oid with free energies ΔG_O1 and ΔG_Oid, respectively, competes with the unfavorable process of forming a loop (ΔG_l). By using this type of lac constructs, Muller et al. (7) measured the in vivo repression of the lac Z gene as a function of the distance between the centers of the O1 and Oid operators.

For a strong auxiliary operator ([N]e^–ΔGOid/RT ≫ 1), as in the experimental conditions analyzed (7), for which [N]e^–ΔGOid/RT ≈ 135, the previous expression simplifies to R_loop = 1 + (e^–ΔG_l^/RT + [N])e^–ΔG_O1^/RT. When the auxiliary operator is not present (ΔG_l = ∞), the repression level is given by R_noloop = 1 + [N]e^–ΔG_O1^/RT.

Results and Discussion

The mathematical expressions connecting the repression level with the molecular properties for a strong auxiliary operator, R_loop = 1 + (e^–ΔG_l^/RT + [N])e^–ΔG_O1^/RT, and for no DNA looping, R_noloop = 1 + [N]e^–ΔG_O1^/RT, have the remarkable property that they can be combined to give the free energy of looping ΔG_l as a function of the physiologically measurable quantities R_loop and R_noloop:

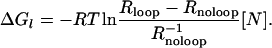[1]

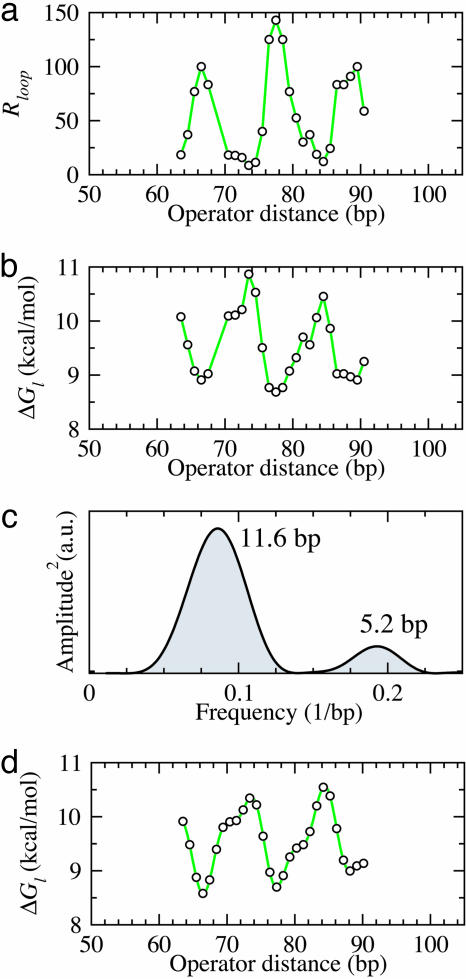
We used this expression with measured repression levels (7) (Fig. 3a) to obtain the in vivo free energies of looping DNA by the lac repressor for different distances between operators (Fig. 3b). This mathematical transformation reveals a wealth of details that were not evident in the repression level curves (7, 9). As expected, the free energy oscillates with the helical periodicity of DNA (7, 9–11) because the operators must have the right phase to bind simultaneously to the repressor. The free energy in a cycle, however, behaves asymmetrically, increasing much faster (≈3 bp) than decreasing (≈8 bp) as the length of the loop increases. A Fourier analysis of the oscillations (Fig. 3c) indicates that, in addition to the component with the helical period (≈10.9 bp), there is a second representative component with period of ≈5.6 bp, which leads to the observed asymmetry (Fig. 3d). This second component has a strong statistical significance (see Appendix I: Statistical Reliability of the Half-Helical-Period Component) and is also present for other experimental data (see Appendix II: Corroboration of the Main Results).

Fig. 3.

From enzyme content of E. coli populations to in vivo DNA looping free energies. (a) Measured repression levels, R_loop, as a function of the distance between operators from Muller et al. (7). (b) Inferred free energies of looping using Eq. 1 and R_loop as in a, with R_noloop = 135 and [N] = 75 nM (7). (c) Fourier analysis of the operator distance dependence of the free energy. (d) Behavior of the two main periodic components of the free energy of looping: ΔG_l(l) = 8.79 – 0.68sin(2π l/10.9 – 0.94) – 0.30sin(2π l/5.6 – 2.32), where l is the distance between operators.

Previous in vivo experiments and analysis for longer loops (>100 bp) used continuum elastic models of DNA to fit the observed repression levels (12–14). Therefore, the conclusions that can be extracted from those studies are constrained by the properties of the DNA models used, which are unable to account for the asymmetry we observe in the oscillations for short loops (Fig. 3b). Our analysis, in contrast, does not depend on any underlying DNA model and is able to capture previously undescribed properties, not considered by current DNA looping models. Recent structural and computational studies on DNA (15, 16) indicate that the loop can be bent and twisted nonuniformly because of different contributions, such as, for instance, the anisotropic flexibility of DNA, local features resulting from the DNA sequence, and interactions with the lac repressor and other DNA binding proteins. Therefore, the behavior we observe might result from the detailed molecular structure of DNA (15, 16) or the intrinsic elasticity of the lac repressor (17).

Another remarkable property of the free energy is that the amplitude of the oscillations is ≈2.5 kcal/mol. Such an amplitude, which is much smaller than predicted from current DNA models (15, 18) and similar to the typical free energies of interaction between regulatory molecules (19), demonstrates that the effects of regulatory molecules are strongly dependent on their precise DNA positioning and at the same time easily tunable and modifiable by their cooperative interactions.

Calibrated models, such as the one we have used here, are widely used in physics and engineering as measuring tools. A well-known example is the measurement of the temperature from the height of the liquid column of a thermometer. In the prototypical model of a thermometer, the temperature in degrees Celsius is given by

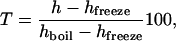where h is the height of the column, and the subscripts label the heights at which water boils and freezes (20). Our results show that analogous measuring tools can also be implemented in cellular systems to infer molecular properties from the observed physiological behavior. Explicitly, the lac operon can function as a sensor to measure in vivo free energies of DNA looping. The results we have obtained with this combined computational–experimental approach challenge the universality of current continuum elastic DNA models at short distances and point to an active role of the physical properties of DNA at shaping the properties of gene regulation.

Appendix I: Statistical Reliability of the Half-Helical-Period Component

To study the effects of noise in the measurements, we consider that the free energy ΔG′_l(l) for a loop length l is affected by a random quantity ξ(l) with zero mean: ΔG_l(l) = ΔG′_l(l) + ξ(l).

The Fourier transform of the deterministic and random components at the frequency v_1/2 of the half-helical-period component are defined as

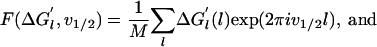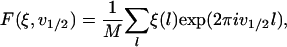respectively, where M is the number of measurements.

Fig. 4.

Corroboration of the main results. (a) Measured repression levels, R_loop, as a function of the distance between operators from figure 4a of Becker et al. (21). (b) Inferred free energies of looping ΔG_l(l), using Eq. 1 and R_loop as in a, with R_noloop = 5 and [N] = 15 nM. (c) Fourier analysis of the operator distance dependence of the free energy. (d) Behavior of the two main periodic components of the free energy of looping: ΔG_l(l) = 9.58 – 0.72sin(2π l/11.6 – 3.08) – 0.28sin(2π l/5.2 – 3.31), where l is the distance between operators.

The power spectrum is defined as the squared modulus of the Fourier transform. Therefore, the relative contribution of the measurement noise is

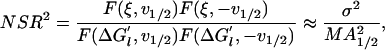where 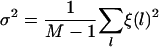is the variance of the random contribution to the measured free energies, and 2A_1/2 is the amplitude of the half-helical-period component.

From the variance of the free energies in table 2 of ref. 6, one can estimate σ = 0.15 kcal/mol. From the data of Muller et al. (7), we obtain 2A_1/2 = 0.30 kcal/mol (Fig. 3d), v_1/2 = 5.6 bp (Fig. 3c), and M = 41 (Fig. 3a). Therefore, the relative contribution of the measurement noise to the power spectrum at the 5.6-bp frequency is NSR = 0.16, which indicates that only 16% of amplitude of the half-helical-period component can be attributed to measurement errors and that the probability of obtaining the 5.6-bp peak of the power spectrum just by chance is effectively zero.

The reliability of the half-helical-period component is much higher than that of single measurements because the evaluation of this component incorporates all of the 41 measurements of the free energy for the different loop lengths. For large M, approximately M > 10, the error can be approximated by a Gaussian distribution, and the probability of obtaining a periodic component as high as A_1/2 because of the measurement errors is given by

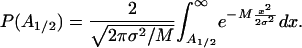Only for high values of the measurement error does this probability become appreciable. For instance, in the previous case, even if the measurement errors had a standard deviation of σ = 0.3 kcal/mol, the probability of obtaining a periodic component with amplitude of 0.30 kcal/mol or higher as a result of the measurement noise would be <0.2% [P(0.3) = 0.0014].

Appendix II: Corroboration of the Main Results

The main results we have obtained based on the classical experiments of Muller et al. (7) are corroborated by the application of our method to the recent experimental data of Becker et al. (21). The experiments of Becker et al. differ from those of Muller et al. (7) mainly in quantitative details. Becker et al. (21) used a weaker main operator, a lower number of repressors per cell, and measured the repression levels for fewer loop lengths. Because all these differences have a tendency to increase the statistical fluctuations, the results obtained with this recent data (Fig. 4) are expected to be slightly less precise than the ones we obtained in Fig. 3.

Similarly as we did in Fig. 3, we used Eq. 1 with the measured repression levels of ref. 21 (Fig. 4a) to obtain the in vivo free energies of looping DNA by the lac repressor for different distances between operators (Fig. 4b). A Fourier analysis of the oscillations (Fig. 4c) also reveals the component with the helical period (≈11.6 bp) and a second representative component with period ≈5.2 bp, which lead to the asymmetric behavior (Fig. 4d).