The Extent of Linkage Disequilibrium in Four Populations with Distinct Demographic Histories

Abstract

The design and feasibility of whole-genome–association studies are critically dependent on the extent of linkage disequilibrium (LD) between markers. Although there has been extensive theoretical discussion of this, few empirical data exist. The authors have determined the extent of LD among 38 biallelic markers with minor allele frequencies >.1, since these are most comparable to the common disease-susceptibility polymorphisms that association studies aim to detect. The markers come from three chromosomal regions—1,335 kb on chromosome 13q12-13, 380 kb on chromosome 19q13.2, and 120 kb on chromosome 22q13.3—which have been extensively mapped. These markers were examined in ∼1,600 individuals from four populations, all of European origin but with different demographic histories; Afrikaners, Ashkenazim, Finns, and East Anglian British. There are few differences, either in allele frequencies or in LD, among the populations studied. A similar inverse relationship was found between LD and distance in each genomic region and in each population. Mean D′ is .68 for marker pairs <5 kb apart and is .24 for pairs separated by 10–20 kb, and the level of LD is not different from that seen in unlinked marker pairs separated by >500 kb. However, only 50% of marker pairs at distances <5 kb display sufficient LD (Δ>.3) to be useful in association studies. Results of the present study, if representative of the whole genome, suggest that a whole-genome scan searching for common disease-susceptibility alleles would require markers spaced ⩽5 kb apart.

Introduction

Whole-genome–association studies using anonymous single-nucleotide–polymorphism (SNP) markers are proposed as a means to search for complex disease-susceptibility genes. However, the feasibility of such studies is presently under debate and is crucially dependent on the extent of linkage disequilibrium (LD) across the genome. There are known to be abundant SNPs spaced throughout the genome that could be used as markers (Human Genic Bi-Allelic SEquences, Human SNP Database at the Whitehead Institute for Biomedical Research/MIT Center for Genome Research, The SNP Consortium Ltd, and CGAP Genetic Annotation Initiative). The SNP Consortium had the original goal of generating a map of 300,000 SNPs (averaging 1 every 10 kb), but it now expects at least to double this (Roberts 2000). Independently, the U.S. National Human Genome Research Institute proposed a 5-year plan to generate a high-resolution SNP map of 100,000 anonymous SNPs. The question remains as to how the markers for such a study should be spaced to maximize coverage while minimizing the amount of genotyping—and hence the cost. Because empirical evidence—which is essential to inform this debate—is very sparse, the present large study has been designed specifically to generate such data.

Whole-genome–association studies require allelic association (resulting from LD) to be detected between the anonymous markers used and the disease-causing allele, so that markers that are physically close to the disease-causing allele will be recognized as being more common among the subjects with disease than among the control subjects. The main questions relating to the markers are (1) whether there is a strong relationship between the distance between two markers and the degree of LD between them and (2) whether this relationship is the same in all populations or whether recently founded populations display LD across greater distances. A third question—when one considers not just LD but also the identification of disease alleles—is the nature of these alleles. Are they, for example, recent or ancient, unique or multiple? Although it is possible that common diseases may be caused by multiple rare disease alleles, it will be very difficult to identify rare low-penetrance alleles by association studies. Therefore, our main focus is on the search for common disease alleles, which we assume will be ancient and similar in behavior to the common SNPs used to detect them.

Kruglyak (1999) used population simulation to suggest a marker design for a whole-genome approach. He used several assumptions: (1) that the human population remained small (N=10,000) until expansion beginning 5,000 generations ago, (2) that all SNPs had arisen only once from a single mutation, and (3) that all SNPs are neutral to selection. The simulations indicated that all common SNPs must be ancient (>10,000 generations old) and that marker pairs >3 kb apart would not demonstrate useful LD. Additionally, unless founder populations were derived from a very tight bottleneck (so that any now-common variant would have been introduced by only a few original founders), they would not be more useful than would other populations when the numbers of markers or subjects needed for an entire scan are considered.

The few existing empirical studies suggest that these predictions may not always be borne out in practice. Peterson (1995) studied microsatellite markers in anonymous regions of chromosome 4 in 50 people from the Finnish founder population. Although tightly linked loci more often showed strong LD, she also found LD between some markers that were >1 Mb apart. Laan and Paabo (1997) also studied microsatellite loci, in a 12.5-Mb region of chromosome Xq13 in males from the Saami, Finnish, Estonian, and Swedish populations with different demographic histories. They detected the most extensive LD (even between markers >10 Mb apart) in the Saami, an isolated founder population that has not undergone recent expansion. Using common SNPs and microsatellites, several researchers have found significant LD between markers separated by distances of 100 kb to several megabase pairs (sometimes approximated as cM) (Peterson et al. 1995; Collins and Morton 1998; Huttley et al. 1999; Wright et al. 1999). Founder populations have proved very useful for the assigning linkage of some complex diseases, such as type 2 diabetes in Mexican Americans (Hanis et al. 1996) and combined hyperlipidemia in Finns (Pajukanta et al. 1998). However, two very recently published papers have suggested that the Finnish and Sardinian populations, at least, do not display more LD than do other populations when markers that are presumed to be ancient are considered (Eaves et al. 2000; Taillon-Miller et al. 2000).

Only a few long-distance physical maps of SNPs are known. In the present study we have used three long, high-resolution, genomic maps in which the marker order is known with certainty. These lie in different chromosomal regions relative to the centromere and telomeres (fig. 1). We have examined the LD relationships between these markers in four populations with different demographic histories. The populations are the East Anglian British (considered to be outbred) and three founder populations: the Afrikaners, the Ashkenazim, and the Finns of Kuopio. We have determined two measures of LD (disequilibrium coefficients D′ and Δ) between all marker pairs and have compared the values obtained across physical distances and between populations, in an attempt to identify the important criteria for designing whole-genome scans. We specifically selected markers with rare-allele frequencies >.1, since these have greater polymorphism-information-content values, which improve the power to detect LD (Terwilliger et al. 1998), and they are most comparable to the common disease-susceptibility polymorphisms that association studies aim to detect.

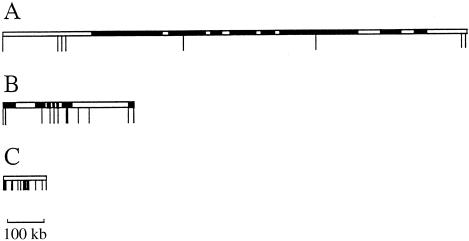
Figure 1.

Relative positions of markers used in each chromosomal region. The blackened sections of the vertical bars correspond to the markers, and the shaded boxes on chromosome 13 and 19 represent gene footprints. Details of each marker, in the order shown, are given in table 1. A, Region 1 (chromosome 13q12-13). Of the eight markers within 1.3 Mb around the BRCA2 gene, the first and sixth markers are microsatellites with bimodal allele distributions. B, Region 2 (chromosome 19q13.2). A 380-kb region with 12 SNP markers including the two SNPs that create the ApoE protein polymorphism is depicted. C, Region 3 (chromosome 22q13.3-ter). Eighteen SNPs in 120 kb are depicted. There are no known genes in this region. All markers were specifically selected to have rare-allele frequencies >.1.

Subjects and Methods

Population Samples and Their Demographic Histories

The East Anglian population consisted of 376 unrelated females taking part in the EPIC study of diet and health (Day et al. 1999), a population-based study conducted in the county of Norfolk in the East Anglian region of southeastern England. Britain and Scandinavia were the last regions of Europe to be populated by Neolithic farmers ∼6,500 years (260 generations) ago (Cavalli-Sforza et al. 1994). Within East Anglia during the past 2,000 years there has been admixture with Mediterranean peoples (Romans), Germanic peoples (Angles and Saxons), Scandinavians (Vikings and French Normans), and people from The Netherlands. The original Neolithic inhabitants may have been largely displaced to more-westerly regions of the British Isles. The population size is estimated to have been 50,000 people at the start of the last millennium, but the marshy geography of the region has meant that the total population has been dispersed as small, isolated communities until the last four or five generations. The population of East Anglia is now ∼500,000 people.

The Afrikaner population was drawn from 115 parent-offspring triads, of whom only the 230 unrelated parents were used in this study. Parents were considered eligible if all four grandparents of their offspring were of Afrikaner ancestry. The Afrikaners are mainly descended from Dutch, German, and, to a lesser extent, French immigrants to the South African Cape. By 1687 the founding population consisted of 90 families. However, there have also been more-recent emigrations (Theal 1964). Although cultural isolation has been strongly encouraged, the degree to which this has been practiced is not known. There are now ∼2 million people of Afrikaner ancestry in South Africa.

The Ashkenazi population consisted of 517 individuals, who were unselected responders from a cohort of 1,200 recent immigrants to Israel from the former Soviet Union (predominantly from the cities of Gomel and Kiev). The Ashkenazim are a European Jewish population who are thought to have migrated to Europe from the Middle East almost 2,000 years ago, although it has also been suggested that they are descended from a tribe of Europeans who converted to Judaism (Koestler 1976). Cultural isolation within this population has also been encouraged. The present worldwide population of Ashkenazim is estimated to be 20 million, but the relevant size of the Ashkenazi population in Gomel and Kiev is unknown.

The Finnish population consisted of 432 unrelated women who had benign breast disease and were residents of the city of Kuopio, ∼300 km northeast of Helsinki. The southern and coastal regions of Finland are considered to have been populated by ∼1,000 founders ∼2,000 years (80 generations) ago. However, migration to the more northern and eastern parts, which include Kuopio, occurred 400–500 years ago (20–25 generations) and involved a smaller subgroup of the Finnish founder population (de la Chapelle 1993; Peltonen et al. 1999). The present size of the population in this region is ∼500,000. Until very recent generations, this population has been geographically isolated.

All DNA samples were extracted in each population's country of origin and were rendered anonymous before analysis.

Markers and Maps

The maps (fig. 1) are 120–1,300 kb in length and have 8–18 biallelic polymorphisms. The marker maps have very different densities, reflecting the various SNP-finding strategies currently in use. No method aimed to comprehensively identify all the SNPs in the region.

Region 1 (chromosome 13q12-13)

Markers were identified as a by-product of the human genome–sequencing project (Sanger Centre). This region on a contig of 14 overlapping clones originally derived from two separate alleles. In 2 of 13 instances, the overlaps contained multiple mismatches as a result of genuine sequence differences between the two clones. Sequence changes that generated RFLPs were chosen, and the allele frequencies were checked in 20 further alleles. We also used two previously identified microsatellite markers that had been sequenced within the contig. The distributions of allele sizes for these markers are bimodal, and, for consistency with the SNPs, we treated these as biallelic (short repeats vs. long repeats) in our analyses. We also used the only common SNP that generates an amino acid substitution (N372H) within BRCA2.

Region 2 (chromosome 19q13.2)

This map was created by GlaxoWellcome as part of a project to identify an SNP in every 100-kb segment (bin) of a 4-Mb region of chromosome 19 (Lai et al. 1998; Martin et al. 2000). A subset of 12 adjacent markers over a region of 380 kb was chosen as being the most densely mapped area within this long region.

Region 3 (chromosome 22q13.3-ter)

This map was generated by the same method used for region 1 during the sequencing of chromosome 22 (Dunham et al. 1999). However, the region chosen for this analysis was a particularly long (120-kb) overlap of two clones from different alleles within the contig (E.D., unpublished data); hence, it gives a much denser map. All the potential SNPs that created RFLPs were identified, and the rare-allele frequency was determined in 20 further individuals.

Genotyping Methods

Details of the markers used and the primers required for their assay are shown in table 1.

Table 1.

Details of Markers and Their Relative Map Positions and Allele Frequencies in Four Populations

		Allele Frequencya
Region and Marker	Position(kb)	EA	Afr	Ash	KF	PCR Primer Sequences	Probe Sequences or RFLP (Fragment Sizes [bp])
Region 1 (13q12-13)b
D13S260	0	.40	.40	.49	.44	F: AGATATTGTCTCCGTTCCATGAR: CCCAGATATAAGGACCTGGCTA	Microsatellite
13-123	160	.31	.33	.45	.35	F: CTGTGGATTTCTGATGGCCTR: AACCACTGTGGGTTTTGAGG	RsaI (197,170, 27)
13-032	170	.29	.34	.38	.33	F: TGGAATTGAGATACAGTGGR: TGCATACACACAATTAGGTC	HincII (170, 140, 30)
13-42	180	.30	.34	.41	.36	F: TGGGTCCTGTGCTTTTCTGAGR: GGAAATGGGTTGAACAAAGGAA	A1: AACCCTCGTAAGTTCCTTAGGCGTTTTTA2: CAACCCTCGTAAGTTCCTTAGGCATTTTT
B2N372H	525	.28	.33	.32	.23	F: CTGAAGTGGAACCAAATGATACTGAR: AGACGGTACAACTTCCTTGGAGAT	A1: TCAAATGTAGCACATCAGAAGCCCTTTGAA2: ATTCAAATGTAGCAAATCAGAAGCCCTTTGA
D13S171	900	.22	.27	.27	.19	F: CCTACCATTGACACTCTCAGR: TAGGGCCATCCATTCT	Microsatellite
13-G	1,325	.42	.46	.49	.39	F: GTATCATACACACACTCACACAGATGTTTR: GTTCAAGGCCAGTCAGCCA	A1: AACCTAATCAAGCTCCAAGGTAAAATCAAATAGAACA2: ACCTAATCAAGCTCCATGGTAAAATCAAATAGAAC
13-H	1,335	.38	.38	.39	.29	F: GCATCTCTCTTGTATGTGATCTCTCATTR: AACAGAGAGAAGACAGGAAAACTAGACC	A1: TTTGAAGATAAAAGGCGAGTGATGAGTGTCA2: CTTTTGAAGATAAAAGGTGAGTGATGAGTGTCC
Region 2 (19q13.2)c
111(ApoC4)	0	.48	.47	.49	.42	F: CCCTCTGGTTCCACCTAGCATR: TCCAGCGACTCATCTTTAGCTTT	A1: AAGGAACCCTGAGCCCCCCACA2: AAGGAACCCCGAGCCCCCC
112 (ApoC4)	5	.36	.36	.37	.45	F: CTATGACGACCACCTGAGGGAR: GCTGTCTTTGGATTCGAGGAA	A1: TGGGTCCGCTCACCAAGGCCA2: TGGGTCCGCGCACCAAGG
(ApoC2)	115	.48	.46	.49	.46	F: TGGCTGTGGAGCGGAAGTR: GGCAGGCTGTCCTCACCA	A1: AACCACTATAAAGCCTCTCTGTGCCCGA2: CAACCACTATAAATCCTCTCTGTGCCCG
(ApoC1)	140	.44	.38	.45	.41	F: AATTCTCCCATCCCACTTTTACCR: CGCTCCCGGTCCTGG	A1: TCCAAGACGATCGACAGAACCACCA2: TCCAAGACCATCGACAGAACCACC
(ApoE) 112	150	.18	.18	.11	.19	F: GGGCGCGGACATGGAR: ACCTCGCCGCGGTACTG	A1: AGGCGGCCGCACACGTCA2: CGGCCGCGCACGTCC
(ApoE) 158	155	.08	.06	.08	.04	F: CCTGCGCAAGCTGCGTAAGR: CGCGGATGGCGCTGA	A1: ACTGCCAGGCGCTTCTGCAGA2: CTGCCAGGCACTTCTGCAGGTC
86 (PRR)	185	.21	.21	.21	.15	F: GGCAGTTTATGTGTGACCTGGAR: TAGGCCGGCGTGGTCA	A1: CCCTCCCGCCCCCGACA2: CCCTCCTGCCCCCGACCTG
87 (PRR)	190	.44	.44	.43	.50	F: GGAACACTGCCTCCCACTTTCR: CAGCCCTAGAGACGGGAGAA	A1: CCAGTGTGCCGTTCCACCTCCA2: TCCAGTGTGCTGTTCCACCTCCC
1046	220	.47	.50	.36	.48	F: TTTTGCCTGTCCTCATTTACACAR: CCCATTTGACAGAAGAAGAGACTCA	A1: CGGGGCACGTCCCCAGCA2: CGGGGCATGTCCCCAGCC
2050	250	.33	.34	.39	.33	F: GACAGGGCATTCTGGTGGAAR: AAGATCACAGGGCTGGCAAG	A1: AGAATTTGGGACCCCAGCCCAGA2: AGAATTTGGGAACCCAGCCCAGC
42079	360	.41	.42	.36	.45	F: TGGGAGATTGAGGCTGTAGTGAR: AGACAGGGTCTCCACTGTGTTG	A1: TGATCATGCCACTGCACTCCAGCA2: ATCATGCCGCTGCACTCCAGC
(PVR)	380	.12	.10	.06	.14	F: CACCATAAATCACATCATTAGCATGAR: CATTCATCTCTAAGCCCTTGGAATA	A1: CCAAGACTCCCAGATCAGCTACCAGA2: CCCAAGACTCCAAGATCAGCTACCAGG
Region 3 (22q13.3-ter)d
70109	0	.24	.29	.29	.26	F: TGAGCAGCCAAGTCTGGACR: ATCCGTGGGTGGAAGGAG	MseI (359, 185, 174)
70332	0.2	.23	.30	.41	.26	F: CTCTGTTCTAGAAGCTGCTCCCR: GCCTTCCTCCAGGAGAGTG	PstI (374, 199, 175)
77634	7.5	.20	.17	.13	.16	F: AACCCAGATGGGTGTTGTCTR: GTCTGGTGCGGTGCTAATG	HindIII (352, 171, 181)
82348	12.2	.14	.14	.12	.14	F: CCATCCTGGGCATTTCAGR: TGACCTTTGTGCAGCCTTC	NcoI (350, 201, 149)
96809	26.7	.21	.16	.21	.20	F: CAGCCACTCCTGACCGCTR: TGTCTGACGGAGAGTTGGGC	A1: CTGCTCTCCTGTAACTGTGACTCAAAGTCCA2: CTCTCCTGTAACTGGGACTCAAAGTCCAC
100008	29.9	.11	.06	.10	.12	F: CAGAGGGAGGGCCTGTCTR: GCAGCTTAGCACCAGCAAG	ClaI (374, 278, 96)
117101	46.9	.06	.04	.10	.10	F: GGCAAATTACTGGGTACTCAGCR: ACAGCTCAGCTTGGCTGG	TaqI (360, 256, 104)
124878	54.8	.32	.37	.29	.32	F: TGTCAAGGACGTCAACAAGGR: GTGTCCCCGCTCTTTCTTC	MspI (357, 191, 166)
132845	62.7	.09	.12	.15	.07	F: CACCCTCCCGCTGCAGR: ATTGAGTTGCTTAGTTTGATTCATGAG	A1: CCACCGCGCCCGGC A2: CACCACCGTGCCCGGCT
133043	62.9	.11	.16	.20	.08	F: TGGAAGAATGACATATTTGTGGATTCR: TGGAAAACAATAATGACCTGCTGT	A1: ATCTGGTCACAATTGATGGCCCATCA2: ATCTGGTCACAACTGATGGCCCATC
136459	66.4	.43	.49	.39	.40	F: GACCCCTGAGCACACAAAGCR: GGCTCCAATTTTGTCCTGTCC	A1: CACCAGCATAAGTCAATCCGAGTGGGA2: CACCAGCATAAGTCGATCCGAGTGGG
136817	66.7	.42	.49	.38	.38	F: AGGAGGTGATGGGCTTTGR: GAAGAAATGAAAACACCGAGCAG	A1: CTGGACGGGTGCTCCAGACCTTCA2: AGCCTGGACGGGTACTCCAGACCTT
138208	68.1	.11	.13	.20	.17	F: TCCTCAGGGTTCAGCCATGR: GCCTTATCCACAACAGCCAAG	A1: CTTCTTAAGGCTGGGTGATTTCCCATCA2: TTCTTAAGGCTGGGTAATTTCCCATCG
143855	73.7	.48	.43	.42	.47	F: CCAGAGTTGGGACCTGGAATACR: CCCTCTTGCTGGGCCAT	A1: TCAAAGTCATATTTCCCTAACGCCCTTAGAA2: TCAAAGTCATATGTCCCTAACGCCCTTAG
146924	76.8	.45	.43	.35	.45	F: AGAAGGGAGTGGTGTGGCAGR: CTCAGGTGATCCACCCACCT	A1: AGTGGCTCACATCGATAATCCCAGCA2: AGTGGCTCACATCCATAATCCCAGC
165653	95.5	.39	.36	.40	.42	F: AACCTTGTCCAGGCCTTCCTR: CAGCAGCCCCAAAACACAG	A1: CCAAGAAACACACAGCTCGTTCATAACTTTCA2: CAAGAAACACACAGCCCGTTCATAACTTT
188866	118.8	.19	.25	.12	.24	F: TAAGACGAGGAAGTCAGCAATGGR: CACATGCCAGGACGGACAT	A1: CCCGCACAGGACTAGAGTCAGGACAA2: CCGCACAGGACTGGAGTCAGGAC
190224	120.1	.21	.24	.14	.24	F: GAGGAAGATGACAACAGAAACGAGR: GGAACTTGGCAGGGAGGTC	A1: CGCTCAGCAGGTGCCCCAA2: CGCTCAGCTGGTGCCCCA

^aEA = East Anglians; Afr = Afrikaners; Ash = Ashkenazim; KF = Kuopio Finns.

^bAround BRCA2.

^cAround APOE.

^dBacterial artificial chromosome bK343C1.

RFLP

PCRs were carried out using AmpliTaq Gold (PE Biosystems), according to the manufacturer's instructions, and the primers (MWG Biotech) listed in table 1. The PCR fragments were then digested with the corresponding enzyme (New England Biolabs) at the appropriate temperature, and the digested fragments were separated on 3% agarose gels (Gibco-BRL).

Microsatellites

D13S260 and D13S171 were first PCR-amplified using AmpliTaq Gold (PE Biosystems), according to the manufacturer's instructions. One of each pair was labeled with a fluorescent dye (FAM or TET) (PE Biosystems). Fragments in the range of 227–243 bp were obtained for D13S171, and fragments of 158–174 bp were obtained for D13S260. A multiplex of both PCR products, together with a GeneScan-500 TAMRA size marker and loading buffer (PE Biosystems) was made and loaded onto a single lane of Sequagel-6 matrix (National Diagnostics) and was detected on a model 373 Sequencer (PE Biosystems). Fragment sizes were analyzed using GENOTYPER software (PE Biosystems).

Taqman

PCRs were carried out using 1× Taqman universal PCR master mix, 900 nM forward and reverse primers, and 200 nM/probe, in a 25-μl reaction. Amplification conditions on an MJ tetrad thermal cycler (Genetic Research Instrumentation) were as follows: 1 step at 50°C for 2 min, followed by 1 step at 95°C for 10 min, and then 30 cycles of 95°C for 15 s and 62°C for 1 min. The two probes for each assay were labeled with VIC, for one allele, and with FAM, for the other allele. The completed PCRs were then read on an ABI Prism 7700 Sequence Detector and were analyzed using the Allelic Discrimination Sequence Detection software (PE Biosystems). Because no controls were included (apart from two no-template controls), the genotypes were manually assigned under dye components.

Statistical Methods

We used two distinct measures of disequilibrium, D′ and Δ, between marker pairs (Devlin and Risch 1995). Each has advantages and disadvantages. Δ has the advantage that population genetics predicts a relationship with recombination fraction: for a panmictic population of constant size N_e, the expected value of Δ² (under the competing effects of recombination and drift) is related to the recombination fraction θ by the formula EΔ²=(1+4N_eθ)^-1. In association studies, Δ is also related to the power of LD mapping—in the sense that the sample size required to detect an association in a case-control study using an anonymous SNP marker linked to a disease-susceptibility gene is increased by a factor of ∼1/Δ², compared with that required when the “true” disease-associated polymorphism (where Δ is the LD coefficient between the two polymorphisms) is used. However, Δ has the disadvantage that the maximum value achievable is dependent on the allele frequencies; therefore, markers can have low Δ values even if no recombination events have occurred between them. D′ has been suggested as an alternative measure because it can vary between 0 and 1 for any combination of allele frequencies; removal of the strong dependence on allele frequency may be expected to give a stronger relationship with genetic distance.

Because only genotype data on unrelated individuals were available, two-locus haplotype frequencies were estimated using the expectation-maximization algorithm (Weir 1996). These estimated frequencies were then used to compute Δ and D′ for all possible pairs of loci within one chromosomal region.

Evidence for differences in the average D′ between populations at different distances were assessed by computation of the statistic S=Σ(D^′_i-D^′)²N_i, where D′_i is the D′ in population i and N_i is the size of population i. The null distribution of S was evaluated by simulation, in which the genotype of each individual was reassigned by random permutation and S was recomputed 10,000 times. We also evaluated the distribution of D′ values for all possible pairs of unlinked markers—this is subsequently referred to as “baseline” LD. The Mann-Whitney one-sided U-test was used to compare the distributions of the D′ in each distance group with the distribution for all possible unlinked marker pairs. This test ignores the nonindependence of the D′ values.

Regression analyses were performed to formally analyze the relationship between D′ and distance. Population genetics predicts that the relationship between LD and distance (or recombination) should be of the following form: D^′=a/[1+b(distance)], where a and b are parameters to be estimated.

Under this model, if there is no relationship between D′ and distance, then b will be effectively 0 For each marker pair, there are four D′ values, one from each population, and one corresponding distance. We denote this group as a “D′ set.” The statistical significance of the fit of the model when b is estimated, compared with b fixed at 0, is evaluated by random permutation of distances in the D′ sets and refitting of the regression.

To determine whether this relationship is dependent on the chromosome of origin, an additional parameter is included in the regression, and the D′ set includes an indicator for chromosome of origin: D^′=a/[1+(b+c)(distance)]. In this calculation, b is the coefficient if the chromosome of origin is 19, and c is the additional factor if the chromosome of origin is 22. (Chromosome 13 is not used in this analysis, and, because too few data points are available, only distances ⩽120 kb are analyzed, so the two chromosome regions have equivalent lengths). To evaluate statistical significance, chromosome of origin was randomly permuted in the D′ sets. In both regressions, 2,000 permutations were performed to estimate the level of statistical significance.

Results and Discussion

Allele Frequencies and Hardy-Weinberg Equilibrium (HWE)

Marker-allele frequencies are similar among the four populations (see table 1); however, because of the large sample sizes, 31 of 38 markers show differences that are significant at the 5% level. The fixation-index statistic averaged over all the markers in all four populations is .0067, and the maximum observed is .017. This is compatible with the values that Cavalli-Sforza et al. 1994) reported for differences between European populations (.016±.002).

The genotypes of all SNPs were tested for conformity to HWE in each population (data not shown). Only one marker (133033, on chromosome 22) appears to deviate from HWE in all four populations. We have since shown this to be an artifact due to a previously unknown rare SNP within 28 bp of marker 133033, which caused miscalling in the Taqman assay. Of the remaining 37 markers, 8% in the East Anglians showed significant deviation (P<.05) from HWE, 8% in the Finns, 19% in the Afrikaners, and 24% in the Ashkenazim. Thus, in both the Afrikaner and Ashkenazi samples, we see more deviations from HWE than we would have expected. Deviation from HWE could be an artifact if poor DNA quality were to lead to difficulties in genotyping, but we have no cause to suspect this in these samples.

LD in the Four Study Populations

The proportions of all marker pairs with significant D′ values are 23% in the East Anglians, 19% in the Afrikaners, and 36% in the Ashkenazim and the Finns. The higher values in the Ashkenazim and the Finns may reflect larger sample sizes—and hence greater power to detect statistically significant values. Only for marker pairs <5 kb apart are mean D′ values in the four populations significantly different from one another (P=.003). Pair-wise D′ values are positively correlated for all pairs of populations (correlation coefficients .41–.64), with no clear differences by marker distance. This reflects the common origin of most haplotypes.

We have concentrated on SNPs with a minor allele frequency >.1 because we expect that these will have characteristics similar to those of the common disease-susceptibility polymorphisms that genomewide association studies are intended to detect. In results similar to those of two recent studies (Eaves et al. 2000; Taillon-Miller et al. 2000), we find little evidence for major differences in the extent of LD among the European populations studied, and this suggests that no large European population will prove to have a specific advantage for association studies focused on ancient, common disease-susceptibility alleles (see the LD and Physical Distance subsection). This is perhaps not surprising, given that common polymorphisms are probably ancient, predating the formation of modern human populations.

LD and Physical Distance

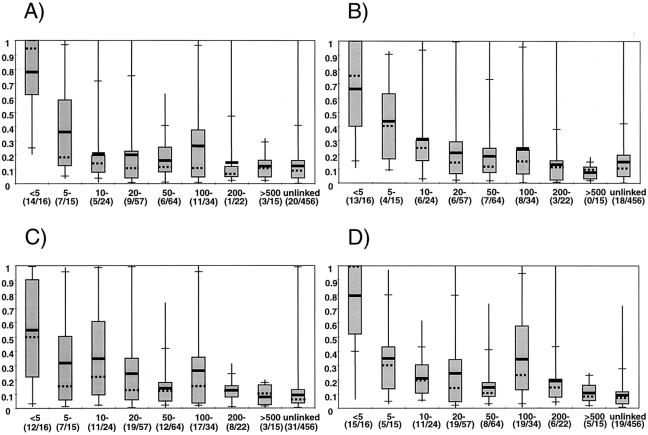
We have summarized the relationship between LD and physical distance as distributions of all D′ values (fig. 2), mean D′ (fig. 3), and proportion of marker pairs with Δ>.30 (fig. 4), against physical distance between marker pairs, for all permutations of pairs. The statistics D′ and D show generally similar patterns. For marker pairs ⩽200 kb apart, the D′ values are significantly higher than those for unlinked pairs (the baseline), in all four populations (all P values ⩽.05) (fig. 2). At 200–500 kb, the Finns still show highly significant differences from baseline (P=.0003), but all other populations show at least borderline differences from baseline at this distance (P⩽.06). For marker pairs >500 kb apart, no population shows any significant difference from baseline (all P values >.25)

Figure 2.

Distribution of D′ LD measure with physical distance (in kb). A, East Anglians. B, Afrikaners. C, Ashkenazim. D, Finns. The black horizontal bars represent the mean D′, whereas the median is represented by a dotted line. The boxes represent the upper and lower 75th percentiles. The horizontal tick marks correspond to the upper and lower 95th percentiles. The proportion of pairs with significant D′ for each distance group is shown in brackets, and the denominator also shows the number of data points in each distance group. Note that the distance groups correspond approximately to a logarithmic scale

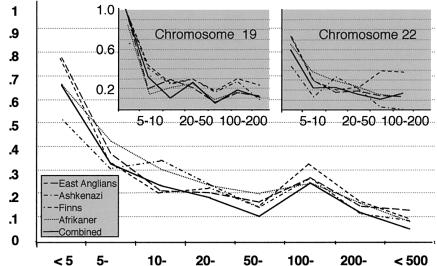
Figure 3.

Mean D′ score by distance (in kb), for all three regions combined. Inset shows the same curves for the individual regions of chromosomes 19 and 22. The asymmetric distribution of the distances between markers across the chromosome 13 map does not generate a continuous curve, so it is not shown here.

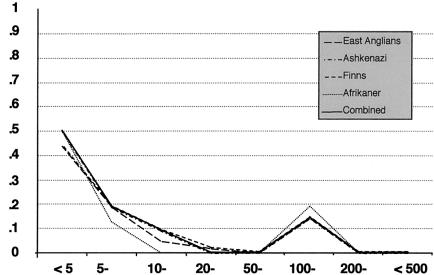
Figure 4.

Proportion of marker pairs with Δ>.3 by distance (kb)

For the combined population samples, mean D′ declines from .68 for marker pairs <5 kb apart to .05 for marker pairs 200–500 kb apart (fig. 3). The regression (see the Subjects and Methods section) provides evidence for an inverse relationship between D′ and distance (b=.0338; P<.0005). The mean D′ is higher for markers 100–200 kb apart than it is for those either 50–100 kb or 200–500 kb apart, although any reason, other than chance, for this finding is presently obscure. There is some evidence for a difference, in the rate of decline of LD, between the chromosome 19 region and the chromosome 22 region (fig. 3) The addition of a chromosome effect to the regression model reveals evidence that LD in the chromosome 22 region declines slightly more rapidly than it does in the chromosome 19 region (c=.485; P=.0005).

To obtain accurate estimates of LD, we used large sample sizes (>230 individuals). Small sample sizes provide estimates of LD that are biased upward, since values of LD must always be positive. This can lead to an underestimation of the rate of decay of LD with increasing physical distance. In general, we find that LD declines rapidly with distance. The mean D′ value for markers 5–10 kb apart is less than half that for markers <5 kb apart (fig. 3). In this respect, our conclusions are consistent with the simulations by Kruglyak (1999), who showed that, when a theoretical population-genetics model is used, a rapid decline in LD at distances >3 kb results. However, Kruglyak’s results also predict that there should be no detectable LD between marker pairs separated by ⩾10 kb, whereas our results indicate both significant LD between marker pairs ⩽20 kb apart and some evidence for LD above baseline, even at distances of 500 kb. These differences could reflect a more complex early demographic history than that modeled by Kruglyak. There is a potential concern that some of the observed LD may be artifactual, resulting from population stratification; however, we find no evidence of significant LD among pairs of unlinked markers (fig. 2), which would have been evidence for such stratification (Lautenberger et al. 2000). Our data also contradict those of Jorde et al. (1994), which suggest that there is little correlation between LD measures and physical distance, for markers ⩽50 kb apart. In contrast, we see a strong relationship between distance and the proportion of markers in LD, at all distances. This difference could be because Jorde et al. studied multiallelic microsatellite markers, which are more mutable—and hence have many newer alleles—rather than the older, common SNPs used here. Taillon-Miller et al. (2000), using SNP markers, found extensive LD in some regions of the X chromosome and much less LD in another region, results suggestive of a recombination hotspot in the second region; whereas the three autosomal regions that we have looked at show uniform, but much less extensive, LD and no evidence for recombination hotspots.

Despite the strong relationship between LD and distance, we find a high proportion of physically close marker pairs that are not in strong LD with one another. As shown in figure 4, at 5 kb apart, ∼50% of marker pairs are not in sufficient LD (Δ>.3) (see the Subjects and Methods section) to be useful for association studies. At 20–50 kb apart, virtually no marker pairs display “useful” levels of LD, in any of the populations. Of course, it is possible that our results are not typical of the distribution of LD over the whole genome. An important issue is whether LD is likely to be greater across coding sequences. None of the markers in this study fall within the same exon, so it is not possible to compare LD within and between exons. However, it is possible to compare both the number of genes in each map and the footprint that their exons leave on the region. There are eight known or predicted genes in chromosome 13q12 (Sanger 2000). The exons of these comprise only 54.8 kb (3.9%) of the region, but they are arranged across ∼80% of the 1.3 Mb studied. In chromosome 19q13.2, there are six known genes: the APO C4/C2/C1/E gene cluster, PRR, and PVR. Nine of the 12 SNPs studied in this region fall within these genes; however, the total amount of coding sequence and its footprint within the region is uncertain. There are no predicted genes or coding sequence within the chromosome 22q13.3-ter region that we studied. The rate of decline of LD with distance is a little slower in the regions on chromosomes 19 and 13 than in the region on chromosome 22 (fig. 3), but it is not clear that this can be attributed to differences in the amount of coding sequence. Our data are generally consistent with other reported data, across coding regions. Thus, Clark et al. (1998) examined all base substitutions detected in a 9.7-kb fragment of the LPL gene in 71 subjects. They found that only 36% of pairs were in strong LD. One interesting exception may be the BRCA1 gene, in which all common coding SNPs across almost 100 kb are in very strong LD (Friedman et al. 1994; Durocher et al. 1996; Dunning et al. 1997).

One way to assess the usefulness of LD for mapping is to assume that one of the markers is the functional (disease-causing) polymorphism, and to ask what increase in sample size would be required for detection of a disease association if a neighboring polymorphism in LD were typed instead. A practical upper limit to the increase in sample size is probably 10-fold for most disorders (Kruglyak 1999), which corresponds to 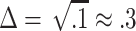; on this basis, only about 50% of marker pairs in our study are in “useful” LD at <5 kb (fig. 4).

The existence of a strong inverse relationship between LD and physical distance means that a complete-genome scan for disease association is theoretically possible. However, if our results are representative of the whole genome, they indicate that a very dense map of markers will be required. We estimate that ∼600,000 markers will be required across the genome. Thus, association studies based on polymorphisms within all known genes, once they are all mapped, rather than on the whole genome, may ultimately prove to be a more effective strategy.