Removing the Sampling Restrictions from Family-Based Tests of Association for a Quantitative-Trait Locus

Summary

One strategy for localization of a quantitative-trait locus (QTL) is to test whether the distribution of a quantitative trait depends on the number of copies of a specific genetic-marker allele that an individual possesses. This approach tests for association between alleles at the marker and the QTL, and it assumes that association is a consequence of the marker being physically close to the QTL. However, problems can occur when data are not from a homogeneous population, since associations can arise irrespective of a genetic marker being in physical proximity to the QTL—that is, no information is gained regarding localization. Methods to address this problem have recently been proposed. These proposed methods use family data for indirect stratification of a population, thereby removing the effect of associations that are due to unknown population substructure. They are, however, restricted in terms of the number of children per family that can be used in the analysis. Here we introduce tests that can be used on family data with parent and child genotypes, with child genotypes only, or with a combination of these types of families, without size restrictions. Furthermore, equations that allow one to determine the sample size needed to achieve desired power are derived. By means of simulation, we demonstrate that the existing tests have an elevated false-positive rate when the size restrictions are not followed and that a good deal of information is lost as a result of adherence to the size restrictions. Finally, we introduce permutation procedures that are recommended for small samples but that can also be used for extensions of the tests to multiallelic markers and to the simultaneous use of more than one marker.

Introduction

The transmission/disequilibrium test (TDT) introduced by Spielman et al. (1993) has become a popular family-based test of linkage between a marker and a susceptibility locus. The attractiveness of the TDT is a result of both its validity in structured populations and its power, which can be much greater than that of conventional linkage tests. The TDT has been extended to multiallelic markers (Bickeboller and Darpoux 1995; Sham and Curtis 1995; Schaid 1996; Spielman and Ewens 1996), to families without parental genotype information (Curtis 1997; Boehnke and Langefeld 1998; Monks et al. 1998; Schaid and Rowland 1998; Spielman and Ewens 1998), and to quantitative traits (Allison 1997; Rabinowitz 1997; Schaid and Rowland 1999). Although the TDT and its extensions that use parental information were designed as tests of linkage in the presence of association, they are also tests of association in the presence of linkage, for samples of unrelated parent/child trios. The advantage of the TDT, in this context, is that it is not sensitive to population stratification in the parental population, which can be a problem for the usual case-control test. For extensions to families without parental-genotype information, the TDT is a valid test of association in the presence of linkage only if samples contain unrelated sibships with exactly two children (one that is affected and one that is unaffected, for tests involving a susceptibility locus). If samples contain larger sibships, then these tests are valid only as tests of linkage.

Tests of association are often used for a candidate gene. Also, once a chromosomal region has been designated, through use of a linkage test, as being of interest, association tests done with the use of markers in the region may be useful for further localization of the susceptibility locus or QTL, since association is thought to exist in human populations for small distances—typically, <2 cM. When the TDT and its extensions are used to test for association, data sets must contain unrelated families of minimal size (one child for families with parental genetic information and two children for families without this information). If families with arbitrary numbers of children have been sampled, then strategies must be used to reduce the data set. One is always reluctant to discard data, because of the probable loss of power; however, if methods are not used to adjust for the correlation between siblings that results from the marker and the QTL being linked, then the false-positive rate for tests of association will be unknown and will be larger than expected.

Martin et al. (1997) generalized the TDT as a test of association in the presence of linkage for a susceptibility gene, for families with an arbitrary number of affected children and with available parental marker–genotype information. More recently, Horvath and Laird (1998), using sibships of arbitrary size, developed a test of association for a susceptibility gene when parental data are missing. In both cases, the authors used the family as the independent sampling unit, to avoid the elevated false-positive rate caused by correlation between sibs. In the present study, we extend the ideas of Martin et al. (1997) and Horvath and Laird (1998), and we propose three tests that can be used for quantitative-trait data and that use information from all children. These tests are valid tests of linkage and association, regardless of the number of children sampled. Throughout the present study, we assume that linkage is present and focus on the test for association in the presence of linkage. For the T_QP test, we use genotype information for parents and for all of their children, whereas, for the T_QS test, we use genotypes for all siblings (with no parental information). Finally, for the T_QPS test, we use a combination of these types of family information. Similar to its treatment in the study by Martin et al. (1997) and Horvath and Laird (1998), the family is treated as the independent sampling unit in all three tests.

In the Methods section below, we introduce each of the three test statistics and derive their distributional properties. Specifically, we show that the test statistics are asymptotically standard normal under the null hypothesis of no linkage or no association. We derive their distribution on the basis of the alternative hypothesis of linkage and association, and, assuming that there is Hardy-Weinberg equilibrium at the marker and at the QTL, we provide formulas to be used for sample-size calculations. Additionally, permutation procedures are given that are recommended for small samples but that can also be used for extensions of the three tests to multiallelic markers and to the simultaneous use of more than one marker.

We then compare the T_QP and T_QS tests with two other nonparametric tests. The first test, which was introduced by Rabinowitz (1997), uses parental-transmission information. The second test, which was developed by Allison et al. (1999), is a permutation test for which only sibship information is used. We will denote these tests as T_R and T_A, respectively. Through simulation, we demonstrate that the false-positive rate increases for both of these tests, when nonminimal families are used. We also compare the power of our tests, in which information from all children is used, to the power of the T_R and T_A tests, in which data sets composed of families of minimal size are used. These comparisons demonstrate the validity of our tests as well as what is gained by use of this additional information. We then provide evidence that our permutation procedures for T_QP and T_QS are valid. Finally, we demonstrate that the validity of the T_QP and T_QS tests is not affected by population stratification.

Methods

Notation

Consider a diallelic-marker locus with alleles A₁ and A₂, with population frequencies p₁ and p₂, and a diallelic QTL with alleles Q₁ and Q₂, with population frequencies q₁ and q₂. Let θ denote the recombination fraction between the marker locus and the QTL. Association—also referred to as linkage disequilibrium—is measured with the use of the disequilibrium coefficient for A₁ and Q₁, denoted as D, where D=Pr(A₁Q₁)-p₁q₁ (Weir 1996). Define μ_rs as the trait mean for individuals with QTL genotype Q_rQ_s, and define σ²_E as the trait-distribution variance within one QTL genotype class. The parameter σ²_E represents all phenotypic variation not attributable to the QTL. We will use the parameterization in which the trait mean of the homozygotes is centered at zero, so that μ₁₁=a, μ₁₂=d, and μ₂₂=-a, where a>0. The phenotypic variance resulting from the QTL can be written as 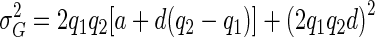. As a measure of the amount of variation caused by the QTL, we use broad-sense heritability, denoted as H², which is the proportion of the phenotypic variance caused by the QTL—that is, H²=σ²_G/(σ²_G+σ²_E) (Falconer and Mackay 1996).

Suppose that there are F families indexed by i. Let the t_i children in the ith family be indexed by j. Unless otherwise noted, all families have the same number of children—that is, t_i=t for all families. Let Y_ij denote the trait value for the jth child in the ith family, and let denote the mean over all children in all families, as computed by . Let X^*_iM (X^*_iF) = 1 if the mother (father) is heterozygous at the marker locus, and let X^*_iM (X^*_iF) = 0 otherwise; denote X^*_iM+X^*_iF as h_i. Let X_ijM (X_ijF) indicate whether marker allele A₁ was transmitted to the jth child by the mother (father), and define as the mean of the t_i values of X_ijM+X_ijF. See figure 1 for an example of notation.

Figure 1.

Example of notation for a family with three children

The null hypothesis is H_o:no linkage or no association, whereas the alternative hypothesis is H_a:linkage and association. The part of the hypotheses concerning linkage is straightforward; however, the part concerning association requires further detail, because of the possibility of population stratification. If there is no population stratification, then the null hypothesis is that there is no linkage or association in the parental population. Alternatively, if there is population stratification, then the null hypothesis is that there is no linkage or association in any of the subpopulations from which parental chromosomes might originate. For clarity of presentation, it is assumed, throughout the present study, that the parental population is homogeneous; however, computations can be extended to a more-complicated population structure. An example is given in Appendix A. For a more-detailed discussion, the reader is referred elsewhere (Ewens and Spielman 1995). When the hypotheses are expressed in terms of parameters, we have H_o:θ=.5 or D=0 versus H_a:θ<.5 and D≠0. In the present study, we assume that the marker and the QTL are in tight linkage and that only the test of association is of interest. For our theoretical derivations and simulations, we assume that the marker and the QTL are both in Hardy-Weinberg equilibrium. This assumption is made for computational convenience and is required only for power calculations.

Test Statistics

We begin with the case for which parental-genotype information is available. If there is no association between the marker allele A₁ and the QTL allele Q₁, then what is transmitted, at the marker locus, to a child from a marker-heterozygous parent neither affects that child’s quantitative trait nor is related to anything that affects the quantitative trait, regardless of whether the marker and QTL are linked. One measure of the marker/QTL relationship is the covariance between the quantitative trait and a variable representing transmissions at the marker locus (Rabinowitz 1997). Consider a family with one parent that is heterozygous at the marker locus—that is, h_i=1. Without loss of generality, suppose that the mother is heterozygous. For each family, the covariance between X_ijM and Y_ij should be zero under the null hypothesis. Since the expectation of X_ijM is .5, an estimate of the covariance is . Likewise, for a family with h_i=2, the covariance between X_ijM+X_ijF and Y_ij should be zero. The expectation of X_ijM+X_ijF is 1; therefore, an estimate of the covariance is 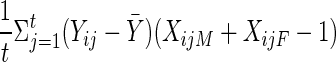. For the ith family, these estimates of covariance can be written, in our notation, as random variable U_i:

Suppose that our data set contains families with at least one parent that is heterozygous at the marker locus; in this instance, for a random family, we have U_i corresponding to h_i=1 or h_i=2. In Appendix B, it is shown that the expectation of U_i for such families is

Hence, we see that the expectation of U_i will be zero, if at least one of the following four scenarios is true:

• 1. The marker and QTL are unlinked (i.e., θ=0.5).
• 2. There is no association between the marker and the QTL (i.e., D=0).
• 3. The QTL has no effect on the trait (i.e., a=d=0).
• 4. a+d(q₂-q₁) is 0 without a=d=0.

Scenario (4), although possible, is not a likely scenario. Scenario (3) contradicts the definition of a QTL so that only scenarios (1) and (2) are pertinent. Furthermore, scenarios (1) and (2) jointly compose the null hypothesis; therefore, discounting scenario (4), the null hypothesis will be true if and only if E(U_i)=0. Although we have assumed, throughout this discussion, that the population is homogeneous—that is, there is no stratification—it is not difficult to show that, if there is population stratification, the expectation of U_i will be zero if there is no association or no linkage within each subpopulation (see Appendix A).

If alleles A₁ and Q₁ are positively associated—that is, if D>0—then, since Q₁ causes high quantitative-trait values (because a>0), we would expect the covariance to be positive. In other words, high trait values will often occur with transmissions of allele A₁, and, therefore, the expectation of U_i will be positive. Similarly, if the A₁ and Q₁ alleles are negatively associated (D<0), we would expect the covariance to be negative. From equation (1), we can see that this is, indeed, often true; however, it is possible to see a negative covariance resulting from a positive association or a positive covariance resulting from a negative association. Nonetheless, in all of these situations, the expectation of U_i will not be equal to zero.

It is thus reasonable to construct a test of association and linkage, on the basis of U_i. We will denote the number of families with one heterozygous parent as F₁ and the number of families with two heterozygous parents as F₂. When the family is noted as the independent unit, a reasonable test statistic is

where 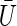is the mean of the F₁+F₂ values of U_i and where Var₀(U_i) is the variance of the random variable U_i, under the null hypothesis. Knowledge of the underlying genetic model would be needed to compute Var₀(U_i) exactly. This type of information will rarely be available; therefore, an estimate must be obtained from the data. Since the expectation of U_i is 0 under the null hypothesis, an estimate of Var₀(U_i) is given as 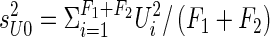. It is noted that the U_i do not have to be identically distributed, as long as their expectation is 0. An example of such a situation arises when sampling families with information on different numbers of children. Using this estimate in our statistic from equation (2), we have

Under the alternative hypothesis, the expectation of U_i will be nonzero, and the estimate of variance will no longer be correct. If the number of families sampled is large, then the distribution of T_QP can be approximated by a normal random variable with a nonzero mean and with unit variance multiplied by a factor that is a function of Var_A(U_i), which is the variance of U_i under the alternative hypothesis, and the expectation of s²_U0 under the alternative hypothesis:

where and 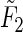are the expected values of F₁ and F₂, respectively. That is,

and

From this approximation, we can compute the power for a given model as well as the average sample size needed to achieve a specified power. Let

and let

so that T_QP≈W_QP×γ_QP. Substituting equations (1), (3), and (4) into the expectation of W_QP from equation (5), we get

Suppose that we are interested in testing the alternative hypothesis that there is positive association (D>0) between the marker allele A₁ and the QTL allele that causes high trait values, and suppose that we are assuming that this corresponds to the expectation of U_i being positive. If we let z_α denote the value such that Pr(Z⩾z_α)=α, where Z is a standard normal random variable, then power is given by

Given a marker and QTL model, along with the type I error rate (α), power can be computed by use of a standard normal distribution.

Of greater interest is the calculation of the sample size needed for a specified power of 1-β—that is, calculation of F for which Pr(T_QP⩾z_α)=1-β. When the above approximation is used, F must satisfy:

Only E(W_QP) is a function of F. Solving equation (6) for F, we get:

It is noted that, although t does not appear explicitly in the formula for F, it will affect the variance of U_i and the expectation of s²_U0. Formulas for these are not shown; however, a program that calculates these quantities—along with power or sample size—is available from the authors (University of Washington School of Public Health and Community Medicine Biostatistics).

Next, consider the case for which no parental-genotype information is available. Since inference of parental genotypes in an unknown mixture of populations is not straightforward, we chose not to infer parental genotypes. We instead used informative families to indicate the presence of at least one parent that is heterozygous at the marker. A family is informative if there are at least two children with differing marker genotypes. The probability of an informative family with t children is

We define the following random variable for the ith family: . This is analogous to U_i with X^*_iM(X_ijM-.5)+X^*_iF(X_ijF-.5) replaced by an estimate. Conditional on the family being informative, the expectation of V_i is

See Appendix C for the derivation. It is interesting to note that

and, so, as t increases, the expected value of Vi approaches that of Ui. Following the same reasoning used in the construction of TQP, we define a statistic on the basis of an estimate of the variance of Vi under the null hypothesis. Without loss of generality, suppose that the first FI of the F families sampled are informative. Under the null hypothesis, the expectation of Vi is zero, so that an estimate of the null variance is s2V0=(ΣFIi=1V2i)/FI. Let be the mean of the Vi for the FI informative families. Our statistic is

T_QS is asymptotically standard normal under the null hypothesis. As was the case for U_i, under the alternative hypothesis, the expectation of V_i will be nonzero, and, for large samples, an approximation can be used to compute power and sample size. Denote the variance of V_i, under the alternative hypothesis, as σ²_VA, and denote the expected number of informative families as . Then the approximate power of the T_QS test, for a test of positive association with type I error α, is given by

where Z is a standard normal random variable. For power equal to 1-β, we have a required sample size of

It is straightforward to combine the two types of family data. Let F_P represent the number of families for which there is parental-genotype information and in which at least one of the parents is heterozygous. Let F_S represent the number of informative families that do not have parental-genotype information. Define the following test statistic as

Our use of this statistic combines the two types of families by giving more weight to the most-sampled type. As before, T_QPS is asymptotically standard normal under the null hypothesis and will have the same properties as T_QP and T_QS. Following the preceeding work for T_QP and T_QS, it is straightforward to compute either the power for a given model or the sample size required for a specified power. The only additional information needed for these computations is what fraction of the families will (or will not) have parental information.

Permutation Procedures

For small samples, permutation procedures can be used to determine significance levels for the T_QP, T_QS, and T_QPS tests. These procedures can also be used to determine either the significance of extensions to multiallelic markers or extensions that utilize more than one marker.

Under the null hypothesis, the probability that a heterozygous parent transmits marker allele A₁ to a child with trait value Y is equal to .5. Thus, if the mother is heterozygous, then, for child j with trait value Y_ij, X_ijM is equally likely to be 0 or 1. If there is only one child, then a permutation procedure can be based on random assignment of X_ijM as being equal to 0 or 1 with equal probability. Complications arise when more than one child in the family has been sampled. These complications are a result of linkage between the marker and the QTL. In the presence of linkage, children with shared marker alleles will have similar quantitative traits, even in the absence of association. This can be taken into account by simultaneous randomization of X_ijM (and, similarly, of X_ijF), for heterozygous parents across the sibship. Consider the X_ijM for family i. Given the vectors T_iM=[X_i1M,X_i2M,⋅⋅⋅,X_itM]^′ and 1-T_iM=[1-X_i1M,1-X_i2M,⋅⋅⋅,1-X_itM]^′, a permutation procedure can be constructed by randomization between T_iM and 1-T_iM. It is easy to show that this procedure is equivalent to randomization of the sign of U_iM. An analogous procedure holds for U_iF with vectors T_iF and 1-T_iF. If the parental contributions to U_i cannot be determined, then the sign of U_i can instead be randomized.

A similar scenario arises when parental-genotype information is not available. First, consider the following form of V_i

where () is the fraction of contributed by the mother (father). Noting that V_i will be nonzero only if at least one of the parents is heterozygous, suppose that only the mother is heterozygous. Randomization between the T_iM and 1-T_iM, for the mother, will be valid under the null hypothesis. While we cannot determine these vectors, this randomization is equivalent to randomization of the sign of V_i. An analogous case exists if only the father is heterozygous. If both parents are heterozygous, then there are four equally likely permutations:

• 1. T_iM and T_iF
• 2. T_iM and 1-T_iF
• 3. 1-T_iM and T_iF
• 4. 1-T_iM and 1-T_iF.

Since we do not know the values for these vectors, we cannot randomize among the four permutations; however, we can randomize between permutations 1 and 4. This is again equivalent to randomization of the sign of V_i.

This results in a unified permutation procedure. Given U_iM, U_iF, U_i, or V_i for a family, a permutation procedure is based on randomization of the sign of the observed value. We suggest use of a Monte Carlo approximation to measure significance. Details are given elsewhere (Monks et al. 1998).

Simulation Parameters

We considered 18 QTL models. Heritability (H²) was equal to .1, .3, or .5. The QTL allele Q₁ had a population frequency of .1 or .5. We studied QTLs with additive, dominant, and recessive modes of inheritance. By setting these parameters, the means for the trait distributions for individuals with QTL genotypes Q₁Q₁, Q₁Q₂, and Q₂Q₂ were uniquely determined. Conditional on an individual’s genotype, the trait distribution is normal, with the appropriate mean and variance, σ²_E, equal to 1.

Marker allele A₁ had a population frequency of .5 or .8 and was completely linked to the QTL. The disequilibrium coefficient was set to 0 for simulations under the null hypothesis, and it was set to its maximum value for simulations under the alternative hypothesis.

We derived formulas for the power of the T_QP and T_QS tests. The powers for the T_R test with t=1 and for the T_A test with t=2 can be computed from the formulas for the T_QP and T_QS tests, respectively. For estimates of significance level, we simulated 1,000,000 data sets, to achieve precision to three decimal places. For estimates of the significance level for the permutation procedures for T_QP and T_QS, we used 10,000 simulated data sets with 99 permutations. For estimates of significance level within a stratified population, we also used 10,000 simulated data sets. All estimates correspond to a one-sided test of positive association, with a significance level of α=.01.

Results

Significance Levels of T_R and T_A for Increasing t

Table 1 contains estimates of the significance level for the T_R test, for a QTL with additive mode of inheritance. Estimates are based on 500 families that all have the same number of children t. We show estimates for t=1,⋅⋅⋅,6. For t=1, the T_R test is valid as a test of association, and, so, our estimates are equal to the actual significance level of 0.01. As t increases, the actual level of significance increases as a result of the nonvalidity of the T_R test. The increase becomes more extreme as heritability, H², increases. In particular, consider the QTL/marker model with Pr(Q₁)=.1 and Pr(A₁)=.5, for sibships of size t=6. The estimate of significance level at H²=.1 is .014, which is much less than the estimate for H²=.3, which is .024. When heritability is .5, the estimate of significance level, .034, is even larger. Estimates of significance are also given, for our T_QP test, for families with t=6. All estimates are equal to .01 and thus support the validity of the T_QP test. The results for a QTL with dominant and recessive modes of inheritance were similar to those presented (data not shown).

Table 1.

Estimates of Significance Level for the T_R Test

			Estimates of Significance Level fora
			TR						TQP
H2	Pr(Q1)	Pr(A1)	t = 1	t = 2	t = 3	t = 4	t = 5	t = 6	t = 6
.1	.1	.5	.010	.011	.011	.012	.014	.014	.010
.1	.1	.8	.010	.011	.011	.012	.013	.014	.010
.1	.5	.5	.010	.011	.012	.012	.013	.014	.010
.1	.5	.8	.010	.011	.012	.012	.013	.014	.010
.3	.1	.5	.010	.012	.015	.018	.021	.024	.010
.3	.1	.8	.010	.012	.015	.018	.021	.024	.010
.3	.5	.5	.010	.012	.015	.018	.021	.024	.010
.3	.5	.8	.010	.012	.015	.018	.021	.024	.010
.5	.1	.5	.010	.014	.018	.024	.029	.034	.010
.5	.1	.8	.010	.014	.018	.024	.029	.034	.010
.5	.5	.5	.010	.014	.019	.023	.028	.034	.010
.5	.5	.8	.010	.014	.019	.024	.028	.034	.010

^aEstimates are based on 1,000,000 simulated samples of 500 families with t children, for a QTL with additive mode of inheritance. Estimates for the T_QP test, with t=6, are also given.

Table 2 contains estimates of the significance level for the T_A test, for a QTL with additive mode of inheritance. Estimates are based on 500 families, all of which have the same number of children. We give estimates for t=2,⋅⋅⋅,6. For t=2, the T_A test is a valid test of association, as our estimates confirm. As t increases, the actual level of significance also increases, as a result of the nonvalidity of T_A. As was the case for T_R, this increase becomes greater as heritability increases. For the same model mentioned above, estimates of significance are .014, .024, and .037 for heritability of .1, .3, and .5, respectively. Estimates of significance are also given, for our T_QS test, for families with t=6; in all cases, the estimates are equal to .01. The results for a QTL with dominant and recessive modes of inheritance were similar to those presented (data not shown).

Table 2.

Estimates of Significance Level for the T_A Test

			Estimates of Significance Level fora
			TA					TQS
H2	Pr(Q1)	Pr(A1)	t = 2	t = 3	t = 4	t = 5	t = 6	t = 6
.1	.1	.5	.010	.011	.012	.013	.014	.010
.1	.1	.8	.010	.011	.012	.013	.014	.010
.1	.5	.5	.010	.011	.012	.013	.014	.010
.1	.5	.8	.010	.011	.012	.012	.014	.010
.3	.1	.5	.010	.014	.017	.020	.024	.010
.3	.1	.8	.010	.014	.017	.020	.024	.010
.3	.5	.5	.010	.014	.017	.020	.024	.010
.3	.5	.8	.010	.013	.017	.020	.024	.010
.5	.1	.5	.010	.017	.024	.031	.037	.010
.5	.1	.8	.009	.017	.023	.030	.037	.010
.5	.5	.5	.010	.017	.024	.030	.037	.010
.5	.5	.8	.010	.017	.024	.030	.037	.010

^aEstimates are based on 1,000,000 simulated samples of 500 families with t children, for a QTL with additive mode of inheritance. Estimates for the T_QS test, with t=6, are also given.

The amount of increase from the expected level of significance, for the T_R and T_A tests, will depend on more than heritability. The QTL model, marker model, number of children, expected level of significance (in this case, .01), and sample size will all affect the increase. Unfortunately, we will not usually know the parameters of our model and, therefore, will not know the impact of nonvalidity. All that can be stated is that the level of significance will be larger than that which is expected.

Comparison of the T_QP and T_R Tests

We have established that the T_QP test is a valid test of association, regardless of the number of children in the family that have been sampled (see the Methods section above). Although it is expected that the T_QP test based on information for all children will be a more-powerful test of association than will the T_R test based on information for a single child, to what extent this will occur is unknown. To investigate this, we compared the power of the T_QP test done with samples of families with t children with the power of the T_R test done with samples of families with one child. Figure 2 contains power curves for the QTL/marker models with additive mode of inheritance and heritability equal to .1, for the T_R test and for the T_QP test, with t = 2–5. It is noted that the T_QP statistic reduces to the T_R statistic when t=1. The four models provide power comparisons over a range of values for the disequilibrium coefficient. Specifically, figure 2A–D shows disequilibrium coefficients equal to .02, .05, .1, and .25, respectively. Panels A–D demonstrate that, as the disequilibrium increases, the sample size required for reasonable power decreases. However, despite the level of disequilibrium, the relationship between the T_QP and T_R tests is clear. Significant information is lost by use of only families of minimal size—that is, families where t=1. As an example, consider figure 2B, for which Pr(A₁)=.5 and Pr(Q₁)=.1. For 80% power, the T_QP test requires 404 families with five children, whereas the T_R test requires 1,813 families or, with respect to genotyping, 2,828 genotypes, compared with 5,439 genotypes, respectively. From a planning standpoint, more than four times as many singleton families, compared with families with five children, need to be collected for 80% power. While it is clear that a good deal of power is gained by use of more than one child per family, it is also apparent that, with each additional child used, there is a diminishing gain in power. The largest gain in power is obtained by use of two children per family rather than one. The increase in power gained from use of three—rather than two—children is also substantial; however, information gained from an increase beyond three children per family continues to diminish. For model 2C, the number of families required for 80% power are 808, 417, 287, 221, and 182 for families with one, two, three, four, and five children, respectively. Approximately half as many families with t=2 are needed, compared with families with t=1. This is a sizable decrease, compared with the ∼20% fewer families required with families with five children compared with those with four children. Although most of the gain in power is derived from increasing t from 1 to 2 and from 2 to 3, it is striking to note that, by use of five children—rather than just one child—per family, only 23% as many families are needed.

Figure 2.

Estimated power for the T_QP and T_R tests of association, for a QTL with additive mode of inheritance and heritability equal to .1. For figures A–D, 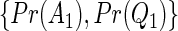was set equal to 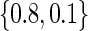, , 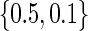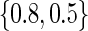and , respectively. The T_QP (dashed lines) test is based on samples of families with two, three, four, or five children (power curves are indicated by increasing power with t), whereas the T_R (dotted line) test is based on families with one child. A solid line indicates power equal to 0.8.

Comparison of the T_QS and T_A Tests

We also compared the T_QS test, in which sibships of size three, four, and five were used, with the T_A test, in which sibships of size two were used. The tests were compared with regard to the QTL/marker models in figure 2 (results not shown). Table 3 contains the values of the ratio F_t/F₂, where F_t is the number of families required for the T_QS test, with samples of sibships of size t, to have 80% power, and where F₂ is the number of families required for the T_A test to have 80% power. Ratios are given for the four models of figure 2, with t = 2–5. The T_QS statistic is equal to the T_A test statistic, when t=2. Conclusions reached from these results are identical to those achieved when T_QP is compared with T_R: considerable information is obtained by use of more than two children per family, and the largest gains in power result from an increase from t=2 to t=3 or from t=3 to t=4. We see that, for each of the models, approximately half as many families are required for T_QS with t=3 as are required for T_A. Approximately one-third as many families are required for T_QS with t=4 as are required for T_A. Both of these decreases in required sample size are considerable; however, we again see that the increase in power and, therefore, the decrease in sample size, diminish as t increases.

Table 3.

Sample-Size Ratios for the T_QS and T_A Tests, at 80% Power

		Ratioa for Models in Figure 2
t		A	B	C	D
2		1.000	1.000	1.000	1.000
3		.506	.510	.511	.522
4		.343	.348	.350	.364
5		.261	.268	.270	.286

^aRatio of the sample size required for the T_QS test, with samples of families with t children, to achieve 80% power to the sample size required for the T_A test, with samples of families with two children. Models correspond to those of figure 2.

Comparison of the T_QP and T_QS Tests

The question arises, with the use of any family-based test, as to how much information is gained by genotyping of parents. To answer this question, we sampled families with a constant number of children t, with t = 2–6. We calculated the number of families, F_P, required for the T_QP test to have power equal to 80%. We then calculated the number of sibships, F_S, needed for the T_QS test to have 80% power. Table 4 contains the F_P/F_S ratio for the 12 marker/QTL models with an additive mode of inheritance for t = 2–6. Now the statistics T_QP and T_QS are composed of random variables U and V, respectively. Since V is an estimate of U, the statistic T_QS is expected to be more variable than is T_QP and, thus, is expected to result in a less-powerful test. The F_P/F_S ratio should therefore be <1. As t increases, the estimate V will improve, and, so, the ratio should increase to one. The results support this. For each of the 12 models, the ratio is smallest for t=2, and it increases with t. Consider, as an example, the model with H²= .1, q₁= .5, and p₁=.5. For t=2, the ratio is .524. In other words, the T_QP test requires only 52.4% of the families that are required for the T_QS test. However, if families with six children were sampled, the T_QP test would require 86.3% of the families required for the T_QS test, thus bringing into question how much effort should be given toward collection of parental genotypes. A few ratios were >1. After further investigation, we have found that, for higher values of heritability, it is possible to have the ratio >1 (results not shown). We also computed the F_P/F_S ratio for the same 12 marker/QTL models with dominant and recessive modes of inheritance (data not shown). Identical conclusions were reached.

Table 4.

Sample-Size Ratios for the T_QP and T_QS Tests, at 80% Power

			Sample-Size Ratioa
H2	Pr(Q1)	Pr(A1)	t = 2	t = 3	t = 4	t = 5	t = 6
.1	.1	.5	.526	.705	.795	.849	.885
.1	.1	.8	.522	.699	.788	.841	.876
.1	.5	.5	.524	.700	.792	.850	.863
.1	.5	.8	.525	.707	.795	.847	.881
.3	.1	.5	.580	.783	.880	.931	.967
.3	.1	.8	.571	.770	.868	.924	.957
.3	.5	.5	.573	.762	.844	.889	.957
.3	.5	.8	.578	.777	.870	.926	.971
.5	.1	.5	.636	.858	.956	1.000	1.040
.5	.1	.8	.630	.850	.951	1.005	1.035
.5	.5	.5	.604	.793	.870	.900	.944
.5	.5	.8	.636	.847	.938	.981	1.021

^aRatio of the sample size required for the T_QP test, with samples of t children, to achieve 80% power to the sample size required for the T_QS test. All models are for a QTL with additive mode of inheritance.

Permutation Procedure for T_QP and T_QS

We provide evidence that our permutation procedures for T_QP and T_QS are valid, by estimation of the significance levels for the T_QP and T_QS tests for the 36 marker/QTL models. Estimates were based on data from 200 families with a constant number of children t. The range of the t value was 1–5, with the exception that T_QS was not applicable for t=1. The 36×5 marker/QTL/sampling models were numbered from 1–180. Figure 3 contains a plot of the estimates of significance levels. Two SD lower and upper bounds are indicated. The significance-level estimates fall satisfactorily within two SDs of .01. This is the case for both the T_QP test (fig. 3A) and the T_QS test (fig. 3B).

Figure 3.

Estimates of the significance level for the T_QP and T_QS tests for the 36 marker/QTL models. Estimates are given for samples of 200 families of constant size t, where t = 1–5. The 36×5 models were numbered 1–180. Note that T_QS is not applicable for t=1.

Validity of the T_QP and T_QS Tests under Stratification

To demonstrate that the T_QP and T_QS tests are valid when there is population stratification, we simulated a population that is a mixture of two homogenous subpopulations. We considered the scenarios where .5 and .75 of our sampled families are from subpopulation 1. For the 12 QTL/marker models with heritability of .1, we simulated samples of 500 families with five children, for all possible assignments of one of these models to subpopulation 1 and of another of the models to subpopulation 2 (132 possibilities). Table 5 contains the mean estimate of the significance level, across these 132 models, for both the T_QP test and the T_QS test, when subpopulation 1 comprises .5 and .75 of the population. We have also given 95% confidence intervals for each mean. Two of the confidence intervals do not contain the expected significance level of .01. We attribute this to our χ² approximation. The estimates deviate from .01 by very little. Furthermore, the deviation is in the opposite direction of that which would be expected as a result of problems with stratification.

Table 5.

Estimates of Significance Level for the T_QP and T_QS Tests in a Stratified Population

Proportion of Sample from		Meana Estimated Significance Level ( 95% CI) for
Subpopulation 1	Subpopulation 2	TQP	TQS
.50	.50	.0097 (.00957, .00991)	.0097 (.00955, .00989)
.75	.25	.0099 (.00975, .01009)	.0100 (.00981, .01015)

^aThe mean estimated significance level for the 132 marker/QTL models (see text for details). Estimates are based on 10,000 simulated samples of 500 families with five children, for a QTL with heritability of .1.

Discussion

Family-based methods have previously been introduced for testing association of markers or candidate genes with a QTL. These tests avoid the increase in the false-positive rate that occurs in the typical case-control test if there is population stratification. However, the current family-based association tests have sampling restrictions that result in a loss of information. However, if these sampling restrictions are not followed, then the false-positive rate of the tests will increase. Furthermore, we have demonstrated, through simulation, that the amount of increase in the false-positive rate will be model dependent. Since the true underlying model is rarely known, a researcher will be unaware of the true effect of nonvalidity. This problem will be compounded as more and more markers or candidate genes are tested, since a researcher will have no sense of how many of their positive results may be in error.

We have developed three tests that are valid tests of association (and linkage) without the sampling restrictions of current tests. In addition, we have shown that a great deal of power is acquired by use of all children. In fact, for all three of our tests, the power increases when more children are used. If association tests are to be performed with the use of a previously obtained data set, then this would imply that all children should be used in the test of association. If a study is being designed, then other considerations, such as ascertainment and genotyping costs, will determine whether fewer large families or more small families should be sampled. For the majority of the models we have considered, the use of families with parental-genotype information will allow for a more-powerful test than will tests in which only sibship information is used. The size of this increase in power is largely dependent on how many children have been sampled. As the number of children in the family increases, the power gained by having parental information diminishes. In practice, a data set will contain families with and without parental genetic information. While one strategy would be to ignore the parental information and to use the T_QS test, we would recommend the use of our T_QPS test. Scenarios do exist where use of sibship information only can result in a more-powerful test than will use of the available parental-transmission information; however, these models generally have high heritability. Although we have shown that considerable power can be obtained by sampling more than the minimal number of children per family, it may be that current tests could be used, in conjunction with special reduction strategies, to reduce families or sibships to minimal size. One strategy would be to randomly sample the minimal number of children from each family and to compute the significance level on the basis of this reduced data set. Other strategies might sample the minimal number of children but might specify that they have extreme trait values (e.g., largest in family, a discordant pair, etc.). These methods should account for some of the power difference seen with use of all children compared with use of the minimal number of children needed (one for T_R and two for T_A). We are currently investigating these strategies.

For simplicity, we have assumed that all families have an equal number of children. If samples of families with an arbitrary number of children are available, then our statistics have the same algebraic form, and only the interpretation of the statistic changes. The mean of the random variable studied (U_i when parental information is available and V_i when sibship information is used) is now a weighted mean across family size, and the variance of the random variable is also a weighted variance across family size. The asymptotics rely on the number of families within each class, where class is defined by family size. If any of the classes have few families, then the normal approximation will be poor, and we would recommend the use of our permutation procedures.

The tests that we have proposed are for a diallelic marker; however, they are easily extended to multiallelic markers. There are two straightforward extensions. A statistic can be computed for each marker allele, and, as an overall statistic, the maximum of their absolute value or the sum of their squares can be used. The permutation procedures can then be used to measure significance. In addition to extensions to multiple alleles, it is possible to extend these methods to the use of multiple tightly linked markers. One could compute a statistic for each marker and then could define an overall statistic—perhaps the maximum or sum across markers. The permutation procedure can be used to measure significance, by simultaneously shuffling across the markers (Lazzeroni and Lange 1998; McIntyre et al., in press).

We have not included a technical discussion of costs. A researcher will have to weigh the genotyping and ascertainment costs, to determine whether resources should be spent on sampling additional children or on sampling parental-genotype information. In terms of power, for our models, larger families with parental-genotype information provide the greatest power; however, costs will determine the ‘‘optimal’’ sampling scheme. Allison (1997) has provided a discussion of costs associated with ascertainment, genotyping, and phenotyping.

Appendix A: Effect of Population Stratification on the Expectation of U_i

Consider a population that is composed of B subpopulations, where the probability of a random family from subpopulation b is φ_b. Suppose that there is random mating within each of the subpopulations, so that each subpopulation will have an expectation and variance of U_i specific to that subpopulation’s allele frequencies and linkage-disequilibrium coefficient. Denote the expectation and variance as μ_b and σ²_b, respectively. The expectation and variance of U_i, for a random family, are therefore E(U_i)=Σ^B_b=1φ_bμ_b and

Under the null hypothesis, there is no association, within each subpopulation, between alleles at the marker locus and the QTL. It follows, from equation (1) in the text, that the expectation of U_i, for each of the subpopulations, is 0—that is, μ_b=0 for b=1,...,B. Thus, the expectation and variance of U_i, for a random family, are 0 and 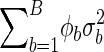, respectively. The estimate of variance used in the construction of T_QP is an estimate of this variance, so that T_QP will be asymptotically standard normal under the null hypothesis. A discussion of the effects of population stratification and admixture is provided elsewhere (Ewens and Spielman 1995).

Appendix B: Derivation of the Expectation of U_i

Families with one or two heterozygous parents provide within-family information about association between alleles at the marker locus and QTL. We begin by considering families with one heterozygous parent. Without loss of generality, assume that the mother is heterozygous for the marker. Then the random variable U_i reduces to 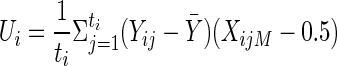. Let p_i|r be the conditional marker-allele probability Pr(A_i|Q_r). Denote the mother’s marker/QTL haplotypes as H_iM1 and H_iM2. Let tr→Q_r represent the event that allele Q_r has been transmitted to the given individual. Denote the probability that a marker-homozygous parent transmits the QTL allele, Q₁, to a child, by use of , where , and denote the probability that it transmits a Q₂, by use of 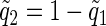. Conditional on X^*_iM=1, X^*_iF=0 and with the assumption that 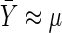and t_i=t,

We obtain the same derivation for families in which only the father is heterozygous. Thus, for families with one heterozygous parent:

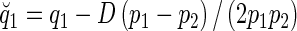For families with two heterozygous parents, we need the probability that a marker-heterozygous parent transmits the QTL allele, Q₁, to a child. Denote this probability as , where , and denote the probability that a Q₂ is transmitted as 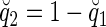. We can write U_i as the sum of two components:

Thus, conditional on X^*_iM=X^*_iF=1 and assuming that the parents are of the same genetic background, we have E(U_i)=2E(U_iM). The above derivation can be used to compute the expectation for U_iM, with one alteration. Transmissions from the other parent are now from a heterozygous parent, and, so, (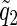) must be replaced by (). From this, we get

Using equations (B1) and (B2), we can derive the expectation of U_i for a family with at least one heterozygous parent:

Thus, we have

Appendix C : Derivation of the Expectation of V_i for an Informative Family

As was the case for U_i, the random variable V_i is the sum of two components, one from the mother (V_iM) and one from the father (V_iF):

where 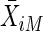() is the part of 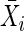corresponding to the mother (father). There are three types of family defined by the number of heterozygous parents. Obviously, if family i has no heterozygous parents, then E(V_i)=0. Next, consider families with exactly one heterozygous parent. Without loss of generality, suppose that the mother is heterozygous. Then, conditional on X^*_iM=1, X^*_iF=0 and letting and t_i=t, we have

Thus, we have

For families with two heterozygous parents, we have E(V_i)=2E(V_iM) (with the assumption that the parents are from the same population). However, E(V_iM) is not that of equation (C1), since we are conditioning on two heterozygous parents. It can be shown that, conditional on there being two heterozygous parents,

The T_QS test is recommended when parental information is not available, and, so, there will be no knowledge of how many of the family’s parents are heterozygous. All that can be determined is whether a sibship is informative for the marker. Thus, we need the expectation of V_i, conditional on a family being informative. Using equations (C1) and (C2), we get

where