A Coalescent Approach to Study Linkage Disequilibrium between Single-Nucleotide Polymorphisms

Summary

We present the results of extensive simulations that emulate the development and distribution of linkage disequilibrium (LD) between single-nucleotide polymorphisms (SNPs) and a gene locus that is phenotypically stratified into two classes (disease phenotype and wild-type phenotype). Our approach, based on coalescence theory, allows an explicit modeling of the demographic history of the population without conditioning on the age of the mutation, and serves as an efficient tool to carry out simulations. More specifically, we compare the influence that a constant population size or an exponentially growing population has on the amount of LD. These results indicate that attempts to locate single disease genes are most likely successful in small and constant populations. On the other hand, if we consider an exponentially growing population that started to expand from an initially constant population of reasonable size, then our simulations indicate a lower success rate. The power to detect association is enhanced if haplotypes constructed from several SNPs are used as markers. The versatility of the coalescence approach also allows the analysis of other relevant factors that influence the chances that a disease gene will be located. We show that several alleles leading to the same disease have no substantial influence on the amount of LD, as long as the differences between the disease-causing alleles are confined to the same region of the gene locus and as long as each allele occurs in an appreciable frequency. Our simulations indicate that mapping of less-frequent diseases is more likely to be successful. Moreover, we show that successful attempts to map complex diseases depend crucially on the phenotype-genotype correlations of all alleles at the disease locus. An analysis of lipoprotein lipase data indicates that our simulations capture the major features of LD occurring in biological data.

Introduction

One of the important goals of modern genetics is to understand the genetic basis of disease. A first step toward that enterprise is locating the gene(s) involved in the generation of a disease phenotype. Knowing the genetics might lead to early diagnosis of risks and possibly even to treatment. Particularly successful were attempts to link RFLPs as markers to certain diseases (Gusella et al. 1983). Although attempts to locate disease genes with an underlying Mendelian segregation pattern were, by and large, successful, little progress was made in the analysis of complex diseases characterized by multiallelic inheritance, low penetrance, and late onset (Collins et al. 1997).

More recently, single-nucleotide polymorphisms (SNPs), which are widely spread throughout the genome (Cooper et al. 1985), have been considered to be suitable tools for association studies (Collins et al. 1997; Landegren et al. 1998). Much of today's research effort goes into the search for SNPs, to build a marker map that spans the whole human genome. The ultimate aim is to provide at least one SNP within each gene. Special activities are under way to find diallelic markers that are variable in most human populations, since such ubiquitous markers facilitate sampling for large association studies.

Different scenarios are imaginable in which SNPs are helpful in locating a gene that produces phenotypically different individuals. The best case occurs if one of the alleles of the SNP creates the disease phenotype. However, this event is unlikely, since most genes are highly polymorphic (Nickerson et al. 1998). The second-best case, again very improbable, is absolute linkage between the disease allele and the SNP. More likely are situations in which we observe only a certain amount of linkage disequilibrium (LD), which can be defined as the difference in the SNP allele-frequency distribution, conditional on whether the wild-type allele or the disease allele is present at the locus (Terwilliger et al. 1998). To evaluate the statistical significance of this difference, a test method is required that compares an observed LD with the LD distribution for an unlinked marker.

Here we assess the probability of detecting a strong association of one or more SNPs with a specified phenotype—for example, a disease. To this end, we simulate the empirical distribution of LD between a disease gene and one or more SNPs, compared with the distribution in a sample of unaffected individuals. To explicitly take into account the demographic history of the sample of affected and unaffected individuals, a coalescent approach is applied (Hudson 1991; Donnelly and Tavaré 1995). The coalescent approach is much more efficient than is simulation of the evolutionary history of a population forward through time.

Contrary to other studies (Thompson and Neel 1997; Rannala and Slatkin 1998; Kruglyak 1999), we do not assume that the mutation to a disease phenotype arose at a fixed point in time, nor do we require that the mutation occurred only once. Thus, our approach mimics situations in which the disease shows allelic heterogeneity. Moreover, the coalescent process allows the efficient estimation of the amount of LD for disease prevalences ranging from rare diseases to common diseases, where prevalence reflects the frequency of chromosomes carrying the disease locus in the population.

Therefore, we provide a unifying framework for dealing with the evolutionary dynamics of marker-disease association for a variety of population histories. Here we present an approach that utilizes most of the known properties of marker loci and disease loci, to evaluate the chances of success of a case-control study.

Methods

For a case-control study, the coalescent theory traces the common ancestry of the locus of interest in affected and unaffected individuals. To reduce the number of parameters, several simplifications are necessary.

First, we fix the prevalence of the disease and the distribution of marker alleles. These distributions can be estimated from given data. Second, we require that they not change throughout time. Note that it is also possible to include the assumption of a time-dependent distribution of markers in our approach. However, this would increase the variance in our results. At least for SNP markers, the assumption of a constant distribution in time seems to be justified by the fact that SNPs are polymorphic in all populations and that therefore they are probably a result of an old mutation that predates the origin of the populations. Moreover, it seems safe to assume that there is little or no selection against the disease allele, as long as we are dealing with common diseases or with diseases having a late age at onset.

Simulation of the genealogy of a sample of size n_W (the number of wild-type chromosomes) and size n_D (the number of disease-carrying chromosomes) is carried out in two successive steps. In the first step, a random genealogy of the entire sample of n_W+n_D chromosomes is generated. Subsequently, the evolution of the SNP is superimposed on the resulting genealogy, thus allowing for mutations and recombination events. Finally, the amount of linkage disequilibrium is computed. The following sections describe each step in more detail.

Building a Genealogy

Throughout the simulations, we consider a large Wright–Fisher population. N(t) denotes the number of wild-type chromosomes at time t (with respect to the disease locus), with f×N(t) being the number of mutant chromosomes (i.e., disease carriers) in the population, where f>0 specifies the relative frequency of the affected chromosomes with respect to the wild-type chromosomes. N(0) and f×N(0) define the number of wild-type and disease chromosomes of the contemporary population. Note that the prevalence—that is, the number of chromosomes carrying the disease locus of interest, f/(1+f)—is independent of the time t and is constant. Moreover, our experimental setup does not require that the sample size n_D reflect the frequency of the disease in the population.

To produce a genealogy, we start with a sample of size n_W+n_D. Going back in time, we find that three events are possible: (1) the coalescence of two wild-type chromosomes, (2) the coalescence of two disease chromosomes, and (3) the mutation of a disease gene to a wild-type gene. Thus, in cases (1) and (2), either the sample of wild-type chromosomes is reduced by one or the disease sample size is reduced by one, whereas, in case (3), the wild-type sample is increased by one and the disease sample is decreased by one. This event is important in the generation of a genealogy that reflects the common history (at the locus of interest) of the affected and unaffected individuals. Since wild-type individuals and disease carriers represent different allelic states at the disease locus, they cannot coalesce. Only when a disease carrier mutates back to a wild type, going back in time, is it possible for the two to coalesce. The process stops when only one lineage is left, the most recent common ancestor (MRCA) of the sample.

Figure 1 sketches the most simple situation: a constant (CONST) population and a sample of n_W=5 wild-type chromosomes and n_D=5 chromosomes showing the disease phenotype. In the wild-type population, the chromosomes coalesce independently of the coalescence events in the population of chromosomes carrying a disease allele. Wild-type and disease lineages can coalesce only in the wild-type population—that is to say, the chromosome carrying the disease allele has to mutate back to the wild type (fig. 1, horizontal dashed line). The two wild-type lineages can now coalesce to form the MRCA. This intuitive description is made more precise in the following.

Figure 1.

Schematic view of the coalescent process in a CONST population consisting of wild-type chromosomes (left) and disease allele–carrying chromosomes (right). From each contemporary group a sample size of five is drawn. Two chromosomes from a sample coalesce at some point in time. Only individuals having the same allelic state can coalesce. Thus, to produce the MRCA of the entire sample, the ancestor of the disease-carrying alleles must mutate back to a wild type (horizontal dashed line).

Let n_W(t) and n_D(t) be the number of wild-type and disease chromosomes at time t that are ancestral to the sample—that is, n_W(0)=n_W and n_D(0)=n_D. Then, according to typical coalescence arguments (Hudson 1991; Donnelly and Tavaré 1995), the rate at which two wild types or two disease chromosomes coalesce equals

and

Mutations from a disease gene to a wild type happen at rate

where μ is the mutation rate of the disease gene per generation. If we label the points in time when one of the three events happened as T₀=0<T₁<T₂…, and if, for each i, we denote by t_i=T_i+1-T_i, the time interval of no change in the number of lineages, then the t_i are distributed approximately according to the following probability-density function

If U is a unit uniform random variable, then solving

for t_i will generate a variate randomly sampled from equation (4) (Donnelly and Tavaré 1995). For equation (5), depending on the population demography, either analytical solutions or numerical solutions are possible.

Once t_i is found, the event that occurs at t_i is determined according to the following probabilities:

the probability for a coalescent in the wild-type sample is

and the probability for a coalescent in the sample with the disease is

Thus, given a scenario about the demographic development of a population, this approach generates a genealogy of a sample of wild-type and disease chromosomes with respect to the population history.

The coalescent approach makes it possible to study the potential to locate a single locus that contributes to a complex disease—for example, a multilocus disease. The genealogy of a complex disease is simulated by assuming that a proportion p₁ of the individuals showing the disease are genotypically wild types at the locus of interest. Thus, a sample of n_D affected individuals is a mixture of p₁n_D wild-type alleles and (1-p₁)n_D disease alleles at that specific locus.

Similarly, one can imagine that, in a sample of individuals showing the wild-type phenotype, a proportion p₂ of them are carrying a disease allele at the specific locus but that the disease either is not manifest at the time of the study or has only low penetrance. Thus, a sample of n_W individuals comprises (1-p₂)n_W true wild-type alleles and p₂n_W disease-allele carriers.

If p₁ and p₂ are known, then the construction of the genealogy is carried out by adjusting the sample sizes for the simulations; that is, the wild-type sample has size n^′_W=(1-p₂)n_W+p₁n_D and the disease sample has size n^′_D=p₂n_W+(1-p₁)n_D. Once the genealogy is built, p₁n_D individuals from the n^′_W-simulated wild types are randomly assigned to the simulated sample of individuals who show the disease. And, vice versa, p₂n_W individuals of the simulated sample of affected individuals are assigned to the simulated wild-type sample. Thus, the genealogy reflects the true relationship among the individuals in the sample, and the reshuffling process after each simulation mimics the uncertainty of a correct assignment to the two categories.

Evolution of the SNP

Once a genealogy is specified, the evolution of SNPs is superimposed on the genealogy. The goal of this exercise is to obtain a sample of wild-type and disease chromosomes, in which each chromosome is associated with a haplotype of SNPs.

Consider a collection of l diallelic markers (SNPs) 1,2,…l, where s_i∈{0,1} defines the (allelic) state of marker i. We assume that markers are ordered along the chromosome where the disease gene is located, marker 1 being next to the gene, marker 2 being second closest, and so on. All the markers are located downstream of the disease locus of interest. The set {0,1}^l comprises all 2^l haplotypes that can be constructed from the markers. Thus, a haplotype of markers constitute a (0,1) sequence of length l.

Let 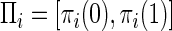be the stationary frequency of marker i(i=1,…,l), and let Λ={λ(s):s∈{0,1}^l} be the stationary distribution of marker haplotypes in the population. By assignment of the haplotype frequencies, the LD between the marker loci is set.

Furthermore, m_i defines the mutation rate (per generation) of marker i, and r_i,i+1 specifies the recombination rate (per generation) between marker i and i+1, where s₀∈{W,D} is the (allelic) state of the disease locus of interest. To simulate evolution of mutation and recombination events, each branch length of the genealogy is rounded to the next smallest integer.

The state of the markers at the MRCA is determined by drawing randomly from the haplotype distribution Λ. If a mutation occurs at marker i, the current state of the marker mutates to the remaining state. A single recombination between markers i and i+1 replaces the current haplotype (s_i+1,s_i+2,…,s_l) by another haplotype randomly chosen from the corresponding equilibrium distribution—that is, the probability to select haplotype (s_i+1,…,s_l) equals

If exactly k recombinations occur and if recombination j∈{1,…,k} happens immediately downstream of the site i_j∈{1,2,…,l} and i₁<i₂<i₃…<i_k, then the haplotype segments (s_i1,s_i1+1,…s_i2-1), (s_i3,s_i3+1,…,s_i4,s_i4-1), and so forth are exchanged for a segment from the corresponding distribution of haplotypes—that is, equation (9) is modified accordingly. The whole process is repeated until the state of the markers at the next branching point of the genealogy is determined.

The outcome of the simulation is a set of n_W+n_D haplotypes consisting of n_D disease genes and their marker haplotypes and of n_W wild-type haplotypes. This set constitutes a random sample of the distribution of the marker alleles in the sample of wild-type chromosomes and disease-carrying chromosomes, conditional on the genealogy.

On the basis of this sample, the amount of LD, d, is calculated for the haplotypes. Let h_W(s) and h_D (s) be the frequencies of haplotype s∈{0,1}^l in the wild-type sample and the disease-carrying sample, respectively; then,

Note that d takes a value between 0 and , the latter being obtained when the wild-type chromosomes and the disease chromosomes are fixed for different SNP haplotypes. The properties of d are well known (Nei 1987).

Simulation Conditions

So far, we have not specified the simulation conditions. First, we need to define the demographic history of the population, to build a genealogy. We define a class of population histories that starts with a given number of chromosomes, N(0), and that shrinks exponentially while going backward in time until time τ (Weiss and von Haeseler 1998). From that point onward, the population remains constant, at a size of . With these parameters, N(t), the number of chromosomes at time t, is defined as

The influence of three population histories on the amount of LD is studied. The first model, CONST, assumes a constant population of 20,000 chromosomes. The second scenario, which uses a population that expanded a long time ago (OLD-EXP), supposes a population of current size of 12×10⁹ chromosomes, representing an autosomal locus in a population of 6 billion people. It started to grow τ=2,800 generations ago, from a population of 20,000 chromosomes—that is, ρ=6×10⁵. Thus, the Paleolithic expansion is modeled. The third case, which uses a population that expanded recently (REC-EXP), assumes that the population started to grow, as a result of the agricultural revolution, from an initial 20,000 chromosomes in the recent past (τ=550) to its present size of 12×10⁹ chromosomes. The disease:wild-type ratio is set to f=1.0.

Experiments were carried out for l=1 marker or l=2 markers. If l=2, the recombination rate between markers was equal to r₁₂=3×10^-5, which is the range over which SNP haplotypes can be typed with one PCR.

To study the influence of population history on the amount of LD, we simulated a sample of n_W=200 wild-type chromosomes and n_D=200 affected chromosomes. The mutation rate of each marker, as well as that of the disease locus, was set to 10⁻⁶/locus/generation. This rate is reasonable for the disease locus; the mutation rate of an SNP does not affect our results as long as it is smaller than the recombination rate (data not shown). For simplicity, we further assumed that Π_i=(.5,.5) for each marker i and that Λ=(.25,.25,.25,.25)—that is, the marker loci are in linkage equilibrium. The recombination frequency varies between 5×10^-5 and 10⁻³, in increments of 5×10^-5.

The influence of the disease:wild-type ratio on equation (10) was investigated by changing f from .01,.02,…,.1 to .1,.2,…,1.0, thereby fixing the recombination rate to 10⁻⁴, whereas the rest of the simulation conditions remained unchanged.

We also examined the effects of different mutation rates at the disease locus. Hence, the rate varied between 10⁻⁷ and 10⁻³/locus/generation, and the recombination rate was set to 10⁻⁴.

To analyze the effect of incomplete genotype-phenotype correlation, p₁ was varied over 0,.1,…,.9. For each choice of parameters, 1,000 genealogies were generated and the relevant statistics were computed.

Results

For most of our work, we compared LDs derived from a CONST population with LDs obtained from expanding populations that started to grow at some well-defined point τ in the past. As can be expected, the simulation results with respect to d and the probability of finding significant LD showed a different picture for OLD-EXP and REC-EXP populations versus a CONST population. Moreover, the amount of LD as defined in equation (10) obviously depends on the rate of recombination between marker locus and disease locus. This observation was virtually independent of the details of the population history. For the sake of clearness, the recombination rate was converted to distances (in kb), following the convention that 1 cM corresponds to 1 Mb. In other words, 1 kb amounts to a recombination rate of 10⁻⁵.

Single Diallelic Markers

If only one diallelic marker (SNP) is considered, then the amount of LD (see fig. 2) declines rapidly as the marker moves farther away from the disease gene. Figure 2 also shows that most information, in terms of d, is lost within the first 5 kb away from the disease locus. If the marker is 5 kb away, then, irrespective of the population history, the average d value decreases to ∼37% of the theoretically maximal value of 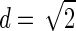for a single SNP. For distances >5 kb, the decline of d depends on the population history. τ (the time when the expansion started) governs this decline. A population with a small τ value (i.e., a REC-EXP population) behaves, by and large, like the CONST model. The LD between marker and disease locus decreases at an intermediate rate between that of the CONST simulation and that of the OLD-EXP simulation. In a CONST population, the average d value monotonically decreases from .56, for a closely linked marker (5 kb), to .19, for a marker 100 kb away. A value of .057 was estimated for an unlinked SNP, which was already achieved for the OLD-EXP model for recombination distances >85 kb. Thus, in a growing population, the potential information about allelic association between a disease allele and a marker is rapidly lost.

Figure 2.

Average LD between an SNP and a disease gene, as a function of the recombination rate. Different demographic histories were simulated: CONST, REC-EXP, and OLD-EXP. The standard errors of the simulations are also shown.

Although the mean d values give some idea about the factors generating LD, it is more insightful to study the (simulated) distribution of d values for different recombination rates, to evaluate the potential usefulness of an SNP for mapping attempts. Figure 3 displays the results in a CONST population for a marker not linked to the disease gene and for markers that are 5, 50, and 100 kb away from the disease locus. All distributions show a maximum at d=.1 and decrease as d increases. Although the probability to observe a d value >.4 is <.001 for an unlinked marker, even for remotely linked markers—for example, 100 kb away—the probability to observe d values >.4 is not negligible. The d distribution for a marker closest to the disease gene (5 kb) extends over the whole range of possible d values; the resulting distribution appears to be almost uniform across the range of possible d values. Very much the same picture emerges if the scenarios OLD-EXP and REC-EXP are analyzed. However, the probability of finding large d values is even smaller than that in the CONST scenario (data not shown).

Figure 3.

LD distribution between the marker (SNP) and the disease gene for the CONST model. The markers were 5, 50, and 100 kb away from the disease gene or were unlinked.

The simulated distributions for a marker a given distance away and an unlinked marker allow an analysis of the power to detect significant association. The distribution of the unlinked marker serves as the null hypothesis (H₀), and the distribution of a marker some distance away from the disease locus represents the alternative hypothesis (H₁). From these distributions, it is straightforward to construct power curves—that is, the probability of detecting a significant association for a marker a fixed distance away from the disease locus. Figure 4 shows the resulting power curves based on a single SNP for the CONST, REC-EXP, and OLD-EXP scenarios. The significance level was set to α=.005. This level is apt for an experimental design in which 10 disease-candidate genes are analyzed with 10 independent markers. The multiple tests carried out for each potential candidate gene would then lead to a nominal significance level of 5%. The significance level chosen here may be a bit too liberal, but, for the sake of argument, we have adopted this value, following standard statistic procedures. For a real study, the significance level should be adjusted according to the costs involved when one is making an incorrect declaration of association. In such situations, α=.0001 is probably more appropriate.

Figure 4.

Power of a single SNP to detect significant LD, as function of distance (recombination rate) to the disease gene. Populations either were CONST or were REC-EXP or OLD-EXP.

However, if the distance of the marker to the disease gene is ∼5 kb, then the probability of detecting a significant linkage is ∼73% in the CONST and REC-EXP scenarios. The power to detect association drops quickly as the distance between the marker and the gene increases. A marker 100 kb away from the disease locus has only a 32% chance to suggest association if the population size is constant. In an expanding population, the power drops more quickly, again dependent on τ, the time when expansion started. In the OLD-EXP population, the power falls to <10% if the distance between marker and disease locus is >40 kb. For a REC-EXP population, the decline in power is less pronounced.

Haplotypes as Marker

Although the detection of LD when only one diallelic marker is used appears to be difficult or restricted to situations in which the marker is in very close association with the disease gene, microsatellites having more than two alleles have been successfully employed to show high amounts of LD (Laan and Pääbo 1997). From this perspective, it is interesting to study the potential to detect a significant association if more than one SNP is used. Hence, we carried out simulations for the CONST, REC-EXP, and OLD-EXP scenarios under the assumption that we can construct haplotypes from two SNP markers that are close to each other (see the Simulation Conditions subsection, above). From two SNP we can construct four haplotypes, which allows the computation, according to equation (10), of the d value. The simulation indicates that the mean d value, as a function of the distance between marker and disease locus, is always larger than the corresponding value for a single SNP (data not shown).

More impressive is the change in the shape of the distribution of d values for markers at selected distances from the disease gene (see fig. 5). Although the distributions in the one-SNP case monotonically decreased, the distributions are now bell shaped, with the exception of the distribution for an unlinked marker; the latter distribution is similar to that of a single SNP. The shape of the distribution and the movement of the mode are already indications that it should be easier to detect association. Thus, the power to detect significant association is substantially enhanced. Using, again, a significance level of α=.005, we estimate a power of 95% in the CONST scenario for the 5-kb marker. This power drops to 69% for the 100-kb marker. Also, in expanding populations (i.e., REC-EXP and OLD-EXP), the power is as high as 92% for the 5-kb marker, but, at a distance >50 kb, it quickly drops to 10% for the OLD-EXP model and stays >35% for the REC-EXP model.

Figure 5.

Empirical LD distributions between a 4-allelic marker (i.e., haplotypes were reconstructed from two SNPs) and a disease gene in a CONST population. The SNP distances of the markers closest to the disease gene were 5, 50, or 100 kb.

Thus, a marker system with more than two alleles or haplotypes is much more efficient in pinpointing any significant association. These results are corroborated by empirical and theoretical analysis (Ott and Rabinowitz 1997; Terwilliger et al. 1998; Kruglyak 1999).

Multiple Disease Alleles

An important question in association studies relates the number of alleles that result in the disease phenotype. In common diseases, it is likely that different alleles in the same gene cause the same disease phenotype. The classification based on the disease phenotype does not result in the identification of a single allele at the disease locus.

Therefore, the disease carriers are not necessarily identical by descent (IBD). Since our model has not incorporated an IBD assumption, we studied the influence that different alleles leading to the same phenotype have on the average d value. To carry out simulations with more disease alleles, we simply increased the mutation rate of the disease gene, assuming that each mutation leads to a new disease-causing allele. Again, we do not specify when these mutations occur. However, we require that the recombination rate between the marker and every disease-causing allele is the same; that is, mutations leading to a disease phenotype should be close to each other—for example, on one recombinational unit.

Figure 6 shows the change in d values as the mutation rate increases. Irrespective of the population history, a high mutation rate causes a smaller d. If the mutation rate is >10⁻⁵, we observe a dramatic decline in the d value. Still, in a CONST population, the average d value is always larger than the corresponding value for the OLD-EXP and REC-EXP populations. The d value for REC-EXP is between the d values for CONST and OLD-EXP. Again, the behavior of d depends on the time τ when the expansion started.

Figure 6.

Average LD between an SNP and a disease gene, as a function of the mutation rate of the disease gene and three population histories: CONST, REC-EXP, and OLD-EXP. The distance between the disease gene and the marker is 10 kb, the sample consists of 200 affected and 200 wild-type chromosomes, and the frequency of the disease allele is .5.

To assist in the understanding of this result, table 1 displays the average number of mutations that lead to a disease allele, for the three population histories. Most important is the transition from a mutation rate of 10⁻⁵ to one of 10⁻⁴. If the mutation rate equals 10⁻⁵, then the number of mutations and the number of different disease alleles, although high, do not lead to a substantial decrease in the d value. If the mutation rate is increased by a factor of 10, then the number of mutations increases approximately fivefold. This large number of mutations decreases the d value drastically.

Table 1.

Average Number of Mutations for Different Mutation Rates and Different Disease Frequencies (Prevalences) and Population Structure

	Mutation Rate per Gene and Generation
Population History and Prevalence	10−7	10−6	10−5	10−4	10−3
CONST:
.5	1.01±.11	1.12±.36	2.11±1.05	9.72±2.76	48.37±5.45
.05	1.00±.03	1.01±.11	1.11±.35	2.11±1.04	9.74±2.74
REC-EXP:
.5	1.02±.15	1.22±.51	3.14±1.48	19.48±4.05	118.69±7.56
.05	1.01±.11	1.14±.32	2.05±1.40	11.35±3.07	84.79±7.18
OLD-EXP:
.5	1.06±.25	1.62±1.00	6.93±2.57	52.60±6.41	195.54±2.53
.05	1.04±.21	1.42±.76	5.29±2.01	40.44±5.67	185.78±4.62

In OLD-EXP and REC-EXP populations, the same mutation rate generates more disease alleles with descendants in the sample than it does in a CONST population. But, because the population is expanding and the genealogy after expansion shows a more or less starlike shape (Slatkin and Hudson 1991), mutations (up to six) that occur during expansion are most likely to affect a single chromosome in the sample and do not dramatically influence the d value that is generated by the old disease allele in the sample. But, if too many mutations occur, the resulting disease-carrying haplotypes share no common history, and they cannot show a high d. For example, if the mutation rate equals 10⁻³, then the d value for the OLD-EXP population equals the value observed for an unlinked marker, thus reflecting the fact that almost every disease carrier exhibits its private allele. In a CONST population, the situation is different. If a mutation has occurred, the mutation is likely to give rise to a disease allele that is represented more than once in the sample. Thus, although different alleles cause the disease, each disease allele occurs frequently in the sample. Accordingly, it takes fewer disease alleles for a similar reduction in LD. But, because expanding populations also accumulate a greater number of different disease alleles, chances are still higher to detect significant association in a CONST population, even when the mutation rate is high.

The number of disease alleles that can exist while still showing a large d value is surprisingly high. For example, in the case of the OLD-EXP scenario, if the mutation rate equals 10⁻⁷, then the disease gene is almost always IBD, with an average of d=.453. If the mutation rate is increased by a factor of 100, then we observe, on average, seven disease-causing alleles, but the d value is reduced to only .424.

Influence of the Prevalence of the Disease

So far, we have assumed that the disease allele has an extremely high occurrence, of 50%. In this section, we analyze the influence of f, the relative frequency of the disease-carrying chromosome, on the d value for three population histories.

Figure 7 shows the results of the simulations. As the ratio of disease phenotype to wild-type phenotype increases, the average d value decreases, and, therefore, the power to suggest association is reduced. Thus, assuming that disease and wild-type chromosomes occur at the same frequency actually results in the worst-case scenario. This effect is substantially less pronounced in the OLD-EXP scenario. Although the d value is still higher with lower f, the effect is small. This suggests that OLD-EXP populations are least suitable for the mapping of rare diseases. The effect of prevalence on the expected number of mutations that generate disease alleles can be seen in table 1. In the CONST scenario, especially, a low prevalence reduces the number of mutations substantially.

Figure 7.

Average LD between an SNP and a disease gene if the prevalence varies and population histories (CONST, REC-EXP, and OLD-EXP) are different. The distance between the disease gene and the marker is 10 kb, the sample consists of 200 mutant and 200 wild-type chromosomes, and the mutation rate of the disease locus is 10⁻⁶. The vertical line marks a change in scale on the horizontal axis.

Other Factors Influencing the Detection Probability

So far, we have discussed the behavior of the d value between one locus that carries disease-causing alleles and the SNP. To account for more-complex situations, with genotype-phenotype correlation <1, we simulated a sample in which p₁n_D individuals showing the disease phenotype are carriers of the wild-type allele at the locus of interest. In real data, this might occur either if multiple genes can cause the disease or if the disease phenotype also has nongenetic causes. In the later case, p₁ is, for example, the frequency of individuals who developed the disease because of environmental factors.

As explained in the Methods section, it is straightforward to build this model into the simulations. Figure 8 shows the result of this on the average d value, as a function of p₁, the proportion of wild-type alleles falsely assigned to the disease-showing group. Note that the case in which p₁=.0 reflects the simulations that we have carried out so far. With increasing p₁, the average d value drops almost linearly, irrespective of the population history. If p₁=.9, then the average d is close to the value for unlinked markers. Thus, complex diseases add an additional difficulty in the localization of disease genes. This result is, of course, not surprising, but the simulations carried out here allow us to add a quantitative component.

Figure 8.

Average d values between an SNP and a disease gene, for varying percentages of chromosomes with disease phenotype and wild-type genotype (p₁). The effect of this misclassification is shown for different population histories (CONST, REC-EXP, and OLD-EXP). The distance between the disease gene and the marker is 10 kb, the sample consists of 200 mutant and 200 wild-type chromosomes, the frequency of the disease allele is .5, and the mutation rate of the disease locus is 10⁻⁶.

The effect of low penetrance or late onset on the average d value is similar to the effect in complex diseases studied above. In this case, one simply assumes that p₂n_W individuals who are carrying the disease allele do not exhibit the phenotypic features of the disease and are therefore classified as wild type.

An Illustrative Example

Simulation studies include simplifications that cannot always be maintained for real data. To verify the basic idea of our approach, we analyzed sequence data from a population-genetic study of the human lipoprotein lipase gene (LPL [Clark et al. 1998; Nickerson et al. 1998]. However, we should be aware that the LPL data were generated for different purposes; therefore, the results are not directly comparable to the simulated results. On the other hand, the analysis gives some qualitative insights into what to expect from real data.

The data set consists of 61 SNPs in which each allele occurs at least three times in the sample. Each of these SNPs was treated as a putative disease gene; one state of the SNP was considered to be a disease-causing allele, and the alternative state was defined as the wild type. The remaining SNPs were used as markers. For marker-and-gene pairs that are physically ≈1 kb (637 pairs), ≈5 kb (424 pairs), or ≈8 kb (166 pairs) apart, the resulting d value was computed. As was also observed under the idealized simulation conditions, the average d value for the LPL data decreases to .49 (at 1 kb), .33 (at 5 kb), or .27 (at 8 kb).

The distribution of d values resulting from this type of data analysis is displayed in figure 9. The shape of the resulting curves resembles our simulation results (see fig. 3). However, we count more marker-and-gene pairs with d values <.1 than are predicted by the corresponding 5-kb simulation. Therefore, it is much more difficult to detect a significant association in this sample. This observation suggests that the physical distance does not reflect the true recombination rate, which is supposedly higher and therefore might indicate the existence of a hotspot of recombination.

Figure 9.

Distribution of LD between fictitious marker-and-gene pairs, for the LPL data (Clark et al. 1998; Nickerson et al. 1998), that are 1, 5, and 8 kb apart. For details, see the text.

To investigate this phenomenon further, we constructed haplotypes from two SNPs that were close together (<5 kb apart) and were ∼5 kb away from the putative disease gene (7,090 trios). The resulting distribution of d values is displayed in figure 10, together with the simulated distribution of a marker 15 or 20 kb away from the disease gene in a REC-EXP population. The average d value of .47 for the LPL analysis falls between the averages from the two simulations, which are .49 and .44 for the 15- and 20-kb cases, respectively. Moreover, among the three scenarios studied, the d-value distribution of a REC-EXP population with a marker pair 15 kb away from the disease gene shows the best least-squares fit to the empirical LPL d-value distribution, whereas the least-squares fit for an OLD-EXP population is substantially worse. Thus, when all due caution is observed, it appears that a recombinational hotspot is hidden somewhere in the LPL gene, which causes the average d value to be similar to the d value that we obtain from simulated markers 15 and 20 kb away from the gene. Moreover, a simple least-squares fit indicates that the individuals from the LPL sample are reasonably well described by a REC-EXP population. However, we did not explore the full complement of possible population histories, and, therefore, the analysis, although promising in its own right, must be viewed with great care.

Figure 10.

Distribution of d values for the LPL data and for a recently expanding population (REC-EXP), when markers are 15 or 20 kb away from the disease gene. Distributions are based on the haplotypes derived from two SNPs.

Discussion

Our results indicate the complexities involved in attempts to map common disease genes. We performed various simulation studies to investigate the effect that (a) distance (recombination rate) between the marker and the locus of interest, (b) population histories, (c) mutation rates, (d) prevalences of the disease, and (e) complex diseases have on the amount of LD. Our analysis, although by no means complete, indicates that the influence of population history on the d value is most substantial. A CONST population always leads to a higher chance of detection of significant association, if the other parameters are unchanged. However, even for a CONST population, the power of our method to compute the haplotype-distribution differences between wild-type and mutant groups is not impressively high except when the marker (SNP) is close (≈5 kb). Thus, it is quite difficult for a diallelic-marker system to locate a disease gene unless the human genome is closely packed with markers. Especially in OLD-EXP and REC-EXP populations, significant association over long distances is rare, as also has been observed by others (Slatkin 1994; Kruglyak 1999). In other words, on the basis of the average mammalian-gene length of 17 kb (Lewin 1994), one SNP per gene does not suffice for detection, with a high probability, of significant linkage. Thus, it is necessary to assess more than one marker per gene. On the other hand, this approach quickly raises the multiple-hypothesis–testing issue.

Although, at a significance level of .005, respectable power is achievable if the marker and the disease gene are closely linked, a whole genome scan with 100,000 SNPs requires a significance level of 5×10^-7 if it is to result in a P value, for the first-order statistic, of ∼5%. The power loss associated with such high levels of significance makes such attempts futile. Attempts that consider LD information from all markers simultaneously are more likely to be successful in such a situation, although the multiple-testing problem remains for these approaches. A possible way to proceed has been proposed by Wiuf and Donnelly (1999). Another sensible strategy is the application of our test procedure to a collection of markers in the vicinity of a set of candidate genes. However, the problem of multiple testing is reduced if haplotypes can be used as markers. We show that it is more sensible to reconstruct haplotypes from two or more SNPs. If this is possible, the power is substantially enhanced.

Our simulations deal mostly with the situation in which the prevalence of the disease in the population equals 50%. As has been shown, this is the worst-case scenario. If the prevalence drops to ⩽10%, then the probability to detect significant association is increased. For example, the average d value for a disease with a frequency of 10% and 10 kb away from the marker is larger than the d value for a disease with a frequency of 50% and 5 kb away from the marker. Thus, it seems easier to locate common diseases that occur at frequencies of ⩽10% in the population. On the other hand, on the basis of our simulations, the optimism that a case-control study with a complete map of SNPs that cover the entire human genome can provide an easy way to map complex diseases is not justified. Thus, our results corroborate results from a similar study (Kruglyak 1999).

Our simulations show that, in more-complex cases—for example, if more than one gene causes the phenotype of interest and, therefore, many people carrying a wild-type gene at one locus of interest are classified as disease carriers—the LD will be further reduced. In such situations, it is much harder to detect a haplotype-distribution difference between wild-type and mutant individuals.

Further difficulties arise from the assumption of a demographic history of the population, which is generally not known and is difficult to infer. To overcome this problem, one strategy might be to infer the population history by using a coalescence-based approach (Griffiths and Tavaré 1994a, 1994b; Kuhner et al. 1995; Weiss and von Haeseler 1998)—by analyzing, for example, either data from mitochondrial hypervariable regions I and II, which are known from worldwide population studies (Burckhardt et al. 1999), or data from other genomic regions, such as variation in either the Y chromosome (Hammer et al. 1997) or the Xq13 region of the X chromosome (Kaessmann et al. 1999). Moreover, the analysis of more than one genomic region, in order to elucidate the demographic history of a population, may help to reduce the large confidence intervals associated with a coalescence-based approach. Nevertheless, once the history is more or less unraveled, the methods outlined here may be applicable to the inference of which conditions are most promising for a disease of interest, to justify a mapping attempt in a population.

Our simulations are based on a great many simplifications, which need to be carefully considered in a real application. However, the LPL analysis shows that, on a qualitative level, the behavior of the d value bears similarities to that in the simulation studies. But, on a more quantitative level, deviations are, in fact, substantial. One reason for these deviations is the nonuniform distribution of SNP-allele frequencies in the LPL data, which reduces the probability of a high LD. In our simulation, we assume a 1:1 ratio of SNP alleles, which is not always true in the LDL data. Moreover, the relatively small sample size of 71 individuals (Clark et al. 1998; Nickerson et al. 1998), as well as the fact that d values derived from the different marker-and-gene pairs are not truly independent measurements, contributes to the observed discrepancy.

Comparing, in a REC-EXP population, the empirical d distribution for 2-SNP haplotypes that are 5 kb away from a putative disease locus, we observed that the average d value of the LPL data falls between the averages observed for 2-SNP haplotypes that are 15 or 20 kb away from the disease locus. Thus, it seems plausible that the physical distance does not reflect the true recombination rate. This estimate is also interesting from an evolutionary point of view, because the result alludes to a recent expansion of humans. This observation certainly deserves a more exhaustive investigation. It would be desirable to develop a method that is based on the approach pursued here, in order to estimate the true recombination rate between a large sample of population-based sequences. Finally, the fact that our simplifying assumptions provide a reasonable description of real data raises hope that our simulations will put us in the position to model the evolution of LD for other population histories and marker configurations.