New Estimates of Intergenerational Time Intervals for the Calculation of Age and Origins of Mutations

Summary

Intergenerational time intervals are frequently used in human population-genetics studies concerned with the ages and origins of mutations. In most cases, mean intervals of 20 or 25 years are used, regardless of the demographic characteristics of the population under study. Although these characteristics may vary from prehistoric to historical times, we suggest that this value is probably too low, and that the ages of some mutations may have been underestimated. Analyses were performed by using the BALSAC Population Register (Quebec, Canada), from which several intergenerational comparisons can be made. Family reconstitutions were used to measure interval lengths and variations in descending lineages. Various parameters were considered, such as spouse age at marriage, parental age, and reproduction levels. Mother-child and father-child intervals were compared. Intergenerational male and female intervals were also analyzed in 100 extended ascending genealogies. Results showed that a mean value of 30 years is a better estimate of intergenerational intervals than 20 or 25 years. As marked differences between male and female interval length were observed, specific values are proposed for mtDNA, autosomal, X-chromosomal, and Y-chromosomal loci. The applicability of these results for age estimates of mutations is discussed.

Introduction

The time interval between two successive generations is not a fixed parameter. Among human populations, maternal age generally varies from 15 years to 50 years, whereas paternal age may reach higher limits (Shryock and Siegel 1976). Because some age groups are more favorable to fertility, age difference between parents and their children is, in most cases, contained within a shorter interval. Still, it is interesting to consider the potential value of a reliable estimate of this interval’s mean length.

In the numerous studies dealing with age estimates of mutations, much attention is given to the calculation of the number of generations or the time period elapsed since a particular event took place (a new mutation, a significant migration movement, isolation, admixture, etc.). However, the estimation of intergenerational intervals is rarely addressed, despite this variable’s direct impact on results. In fact, most authors use the mean value of 25 years (recent examples include studies by Moisio et al. [1996]; Thompson and Neel [1996, 1997]; Varilo et al. [1996]; Labuda et al. [1997]; and Kittles et al. [1998]), while others use the lower value of 20 years (Comas et al. 1996; Slatkin and Rannala 1997). A lack of details regarding the calculation of these intergenerational intervals exists, because precise estimations can only be obtained in populations for which reliable demographic records are available (which is not the case for prehistoric populations).

In agreement with a study by Forster (1996) that yielded a mother-daughter interval of 30 years in a sample of 17th–19th century North German and Danish rural women, and in keeping with Cavalli-Sforza and Bodmer (1971), who suggested a value of 29 years for female generation length (albeit without further justification), we show that using ⩽25 years as a mean value for intergenerational intervals may in fact be an underestimate. By using data from the BALSAC Population Register, which contains information on a relatively large and complete population for several centuries, we analyzed the values and distribution of thousands of intergenerational intervals in ascending and descending lines. Particular attention was given to the difference between maternal and paternal lineages. New values for intergenerational intervals are suggested, and their reliability and impact on the age estimates of mutations are discussed.

Material and Methods

Saguenay Population and the BALSAC Population Register

The Saguenay region (pop. 296,000) is located on the north shore of the St. Lawrence River, northeast of Quebec City. French Canadian settlement in this region began in the late 1830s (Roy et al. 1988). The predominantly Catholic population (98%) maintained a high growth rate up until the early 1960s, averaging 3.3% per year between 1860 and 1960 (Pouyez and Lavoie 1983). This rapid growth was primarily the result of high fertility levels.

The BALSAC Population Register was initiated in 1972 (Bouchard 1992; Bouchard et al. 1995). The main purpose of this database is to support research aimed at describing the formation and evolution of Quebec’s population by using information on individual and family life courses. Initially, the register was constructed to encompass the entire population of the Saguenay region, from 1842 to 1971. All parish records dating from this period have been computerized and linked, and the register is now being expanded to all regions of Quebec for the 19th and 20th centuries. The linkage process of these records is carefully performed. The entire data set is submitted to various validation and consistency checks at each step of the family reconstitution to minimize the occurrence of false links, such as those resulting from illegitimacy or adoptions (Bouchard 1986). It is estimated that the proportion of accurate links is >99% (Bouchard 1989). At present, the database contains nearly 2,000,000 records, of which 700,000 have already been linked (Bouchard 1998).

An important feature of the BALSAC register is that it allows researchers to conduct longitudinal studies covering several generations. For instance, intergenerational studies of the Saguenay population can be performed for up to five or six generations. With the expansion of the database, this time span will increase as well.

Family Reconstitution of Saguenay Male and Female Cohorts

Family reconstitution of all parents born in the Saguenay region between 1850 and 1880 was performed by using data from the BALSAC Population Register. Birth and marriage dates were used to calculate ages at various events. Mother-child and father-child birth intervals were analyzed separately.

Nearly 20,000 births were recorded in the Saguenay population between 1850 and 1880; however, because of factors such as child mortality and outward migration of surviving children, less than half (44%) of that number subsequently married in the region. Of those who married in the region, 3,290 females and 3,367 males had at least one child who also married in the region. Fertility was high: on average, these parents had 9.5 children, half of whom married in the Saguenay. Intergenerational intervals between parents and children were investigated. Several family life-cycle events were considered to estimate the intervals: ages at marriage, ages at the births of the first and the last children, and mean ages at the births of all children were measured. The relation between some reproduction parameters (numbers of children and married children) and mean age at childbearing was analyzed. In addition, some intergenerational comparisons were done.

BALSAC-RETRO Genealogical Database

BALSAC-RETRO is a peripheral database of the BALSAC Population Register (Jomphe and Casgrain 1997). It was developed through various research projects involving genealogical analyses (for example, see Heyer and Tremblay 1995) and is still expanding. At present, the database contains linked information on more than 120,000 marriages going back as far as the late 16th century.

Genealogical Sample

The ascending genealogies of 100 randomly chosen individuals (50 couples) who were married in the Saguenay region between 1900 and 1974 were used for this study. These genealogies have an average depth of 9 generations, but many lineages go as far back as 12 or 13 generations. Overall, 237,822 ancestors were identified in the 100 genealogies, corresponding to 15,752 distinct individuals with a mean number of appearances of 15.

Intergenerational intervals were calculated by use of the difference between marriage dates of parents and children. As marriage dates were not available in all instances (mainly for earlier records), we were able to calculate 10,558 distinct intervals, among which 4,960 were male intervals (on the basis of sex of the child) and 5,598 were female. Distributions of male and female intervals were analyzed separately. As we were also interested in the variability of the mean intervals among the 100 genealogies, we computed the mean interval length within each genealogy, counting an interval as many times as it appeared. We also measured the mean length of intervals among the maternal (mother-daughter) and paternal (father-son) lineages. Lastly, intervals in the descending lines of founding ancestors who married before the year 1700 were examined. As 17th-century founding ancestors contribute to >80% of the contemporary Saguenay gene pool (Heyer et al. 1997), the relationship between the average length of the intergenerational intervals in these founders’ descending lines and their genetic contribution to the 100 Saguenay individuals was investigated.

Results

Age of Parents at Various Family Cycle Events

Figure 1 shows the relative distribution of the 6,657 Saguenay parents according to their ages at marriage, their ages at the births of their first and last children, and their mean ages at the births of all their children. These results clearly show the relatively large fertility period characterizing the 19th-century Saguenay families. In most cases, the first child was born during the year after marriage; the average age of the mother at the birth was 22 years, and that of the father was 24 years. Owing to mortality rates during the reproductive period, the variability of the age at the birth of the last child is larger than that of the age at the birth of the first child. Saguenay women gave birth to their last child at the average age of 39 years, but most surviving women remained fertile until their late 40s. As expected, the age of fathers at the birth of their last child reached higher limits than the mothers’ (average: 44 years) and showed more variability.

Figure 1.

Distribution of parents according to their ages at various events.

The long time span separating the births of first and last children shows that the intervals between generations vary greatly. This is quite typical of a natural-fertility population in which virtually no contraception methods are used. As a result, the average interval between parents and children, measured here by using the mean age at childbearing, reached 30 years for mothers and 34 years for fathers. Figure 1 also indicates a mean age at childbearing >30 years for half of the mothers (34 years for fathers). Mean age was ⩽25 years for only 13% of mothers and 5% of fathers; the percentage of parents with a mean age of <20 was practically nil.

Mean Age at Birth of Children and Mean Numbers of Children and Married Children

The relationship between average intergenerational intervals and reproduction levels is shown in figure 2. The mothers with the highest fertility had an average maternity age of 29–32 years. These mothers had 11 children, on average, and represent 40% of all mothers. Mothers with a mean age at childbearing of ⩽25 years had ⩽6.3 children, on average. The mean number of children rises with the average paternity age until ∼40 years. At that age, fathers had nearly 12 children, on average. Between the mean paternity ages of 32 years and 44 years (60% of all fathers), the average number of children is always >10. At age 25 years, this number barely reaches four.

Figure 2.

Mean numbers of children and married children according to parents' mean age at birth of children.

Because only half of all children married in the region, it is also useful to consider the average number of these married children. This parameter is interpreted as an effective reproduction index, because most of these children will themselves bear children, thereby contributing to the gene pool of the region. As figure 2 shows, the relationship between the average number of married children and the average age at childbearing is very similar to the previous one. The highest levels of reproduction belong to mothers whose average maternity age was 29–32 (∼5.5 married children) and to fathers whose average paternity age was >32 and <44 (⩽6.5 married children). Again, these parents represent a large portion of all parents. At the opposite, mothers and fathers whose average age at childbearing was <26 years had fewer than three married children, on average.

Intergenerational Comparisons

To compare the parents’ reproductive behavior with that of their children, we calculated the same parameters among the second and third generations, the latter of which numbered over 100,000 members. Results (not shown here) indicated that intergenerational intervals between second and third generations were almost the same as those between first and second generations. Except for the average numbers of children and married children, which were seen to decrease slightly, there were no significant changes in the distribution of ages at childbearing.

Distribution and Mean Values of Intergenerational Intervals in the 100 Ascending Genealogies

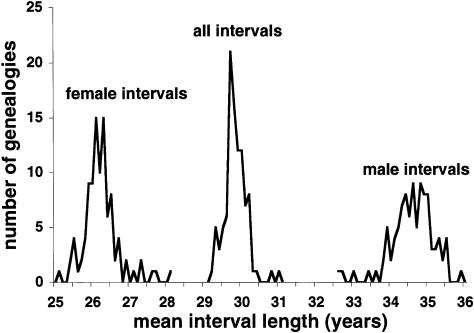
The distribution of the 10,558 intervals between parents’ and children’s marriage dates found in the 100 Saguenay ascending genealogies appears in figure 3. The highest frequencies were found between 25 and 35 years; 46% of all intergenerational intervals were in that bracket. Of the remaining intervals, <21% of the intervals were <25 years, whereas 33% were >35 years (the longest interval was 79 years). On average, the interval length was 31.7 years.

Figure 3.

Distribution of the 10,558 distinct intergenerational intervals in the genealogies.

Figure 3 also shows that important differences appeared when male and female intervals were considered separately. The variances of the two distributions were similar, but, on average, female intervals had a shorter length: 28.9 years, compared to 34.5 years for male intervals. In both cases, the proportion of intervals >25 years was high: 68% of female intervals and 92% of male intervals. It is also interesting to note that 44% of the male intervals were >35 years.

There was a certain variability in the average intergenerational-interval length among the genealogies, though the differences were relatively small (figure 4). Three-quarters of the genealogies had a mean interval length of 30.2–30.7 years (a mere 6-mo difference). This range was slightly larger when male and female mean intervals were considered separately: in 76% of the genealogies, the mean female interval was between 25.8 and 26.6 years (mean 26.2), and, in 75%, the mean male interval was between 34.2 and 35.3 years (mean: 34.6). Though the genealogies were not fully independent (a number of ancestors appeared in more than one genealogy), these results indicate that there was a strong stability in the average intergenerational time span.

Figure 4.

Distribution of the 100 genealogies according to mean length of intergenerational intervals.

Maternal and Paternal Lineages

Mother-daughter and father-son lines were investigated to determine whether there were differences in intergenerational intervals between female- and male-only lines over a large number of generations. To minimize random variations, only those genealogies where at least five intervals could be calculated were taken into account; thus, calculations included 97 genealogies for maternal lines and 87 for paternal lines. Results yielded a mean interval length of 26–32 years for >80% of maternal lineages (mean for all lineages: 28.7 years). For the same proportion of paternal lineages, the mean interval length was 31–38 years (mean for all lineages: 35.0 years).

Variability of Interval Lengths in 17th-Century Ancestors' Descending Lines

Among ancestors with a recorded date of marriage, we identified 457 distinct founders who married before the year 1700. Intergenerational intervals in the descending lines of each of these ancestors were measured. The distribution of these ancestors according to the mean interval length of their descending lines is presented in figure 5. Again, most of the mean interval lengths hovered around 30 years: 68% were between 28.5 and 31.5 years. None of the ancestors’ descending lines had a mean interval length <25 years, and some of them reached as high as 37 years.

Figure 5.

Distribution of the 457 founders according to mean length of intergenerational intervals in their lineages.

As mentioned previously, the early founders of the Saguenay population contributed a major part of the contemporary gene pool. However, among these founders, the individual genetic weights vary greatly, since a few individuals explain a large proportion of the total genetic contribution. For instance, the top 5% of the group have a combined genetic contribution corresponding to 55% of the founders’ total genetic contribution. It takes only 30% of all founders to reach 90% of the founders’ total contribution, meaning that most founders have a very low contribution. We wondered whether there could be a link between a founder’s contribution and the mean interval length in his descending lines. Can we assume, for example, that if the mean interval length in the descending lines of a given founder has a lower value, the genetic contribution of this founder should be higher than average? According to the results appearing in figure 6, there is no such relation. Those founders with the shortest interval lengths did not have a higher genetic contribution. Also, founders with the highest intervals lengths did not have the lowest contributions. In fact, the highest genetic contributions were associated with average interval lengths (∼30 years).

Figure 6.

Relation between founders' genetic contribution and mean length of intergenerational intervals in their lineages.

Discussion

Table 1 summarizes the findings mentioned previously. Regarding the average length of intergenerational intervals, both methods (family reconstitutions and ascending genealogies) clearly indicate that this average length is significantly higher than the widely used value of 25 years. This latter value corresponds, in fact, to the average parental age at birth of the first child (23 years for mothers and 26 years for fathers).

Table 1.

Summary of Intergenerational Intervals Measurements

Measurement	Mean Value (years)
By family reconstitutions:
Mothers:
Age at first birth	22.8
Mean age at children's births	30.3
Age at last birth	38.7
Fathers:
Age at first birth	26.2
Mean age at children's births	34.4
Age at last birth	43.7
By genealogical reconstructions:
Distinct intervals:
All intervals	31.7
Female intervals	28.9
Male intervals	34.5
Mean value per genealogy:
All intervals	30.4
Female intervals	26.2
Male intervals	34.6
Maternal lineages	28.7
Paternal lineages	35.0
Founders' lineages	30.2

The observed differences in the mean values obtained when calculations were performed on the basis of distinct intervals, and when they were performed on the basis of the mean interval length within each genealogy (where a parent-child interval was counted as many times as it appeared in the genealogy) showed the impact of the variability in the number of appearances of each ancestor. In table 1, we observe an important difference in the results obtained with the two methods of calculation for female intervals (means 28.9 and 26.2), indicating that for the most frequent female ancestors, the average interval was shorter. As the most frequent ancestors are found primarily among the first settlers of the colony, their shorter intervals can be explained by historical context: it has been shown that in the first decades of the colony, a shortage of women led to a noticeable decrease in the age at marriage (Charbonneau et al. 1993).

As indicated in table 2, our results point toward an average value of 32 years for intergenerational time intervals. This value should be increased to 35 years in studies focusing on Y-chromosome loci, whereas studies concerned with mitochondrial DNA should use a value of 29 years. As for X-chromosomal loci, the proposed value of 31 years is obtained from the weighted average of male and female intervals, as two-thirds of X chromosomes are transmitted by mothers and one third by fathers.

Table 2.

Intergenerational Intervals by Type of Locus

Type of Locus	Intergenerational Interval (years)
Autosomal	32
X chromosomal	31
Y chromosomal	35
Mitochondrial	29

We therefore suggest that a minimal value of 30 years would constitute a more appropriate estimate of intergenerational time intervals than 20 or 25 years. To our knowledge, intergenerational time intervals seldom have been measured and never before on such a large sample. Choosing an average value of 30 years between generations, instead of 25 years, increases the time depth for a given number of generations by 20% (50% if compared with 20 years). This difference may have a significant impact on mutation-age estimates.

Demographic Characteristics of the Quebec Population from the 17th to the Early 20th Century and Applicability of the Results

Although some demographic parameters of the Quebec population from the 17th to the early 20th century may differ from those of other populations, we can assert that this population was living in a demographic context very similar to the one characterizing many ancient populations. This context includes high fertility (nearly natural fertility levels), high mortality (at least in comparison with present-day standards), and a relatively low age at marriage. From the available data, we know that several European populations in the last 500 years have been living under similar conditions (Rallu and Blum 1991). However, we cannot measure precisely the extent to which these conditions can be applied to older populations.

According to some paleodemographic studies, mortality was probably higher, on average, in prehistoric times than it was in the past few centuries (Alesan et al. 1999; Boquet-Appel and Bacro 1997). However, the estimation of mortality levels based on findings from human skeletons remains a perilous exercise and is subject to high risks of error (Konigsberg and Frankenberg 1992; Saunders et al. 1992; Boquet-Appel and Masset 1996). Moreover, high mortality does not automatically reduce the length of intergenerational intervals. The main factor causing a low life expectancy at birth in a population is a high level of infant mortality (Shryock and Siegel 1976). Those who survive beyond infancy might be expected to live much longer, on average. Boquet-Appel and Bacro (1997), working on a sample of Neolithic skeletons, estimated life expectancy at birth between 25 and 28 years while, at age five, it reaches ∼43 years. In the 19th century Saguenay population, children who were still alive at age 15 years (65% of the initial cohort) lived, on average, another 48 years (table 3). In these conditions, only a portion of a given generation contributes to the birth of the next generation, as shown in table 3 (see effective population–size estimates). Incidentally, this participation varies according to mortality hazards in adulthood. All other things being equal, those who die younger have fewer children, and intergenerational intervals in their lineages are shorter. Conversely, those who survive beyond their reproductive life have, on average, higher intergenerational intervals and also the highest number of children. Proportionally, these survivors have a greater genetic contribution to subsequent generations.

Table 3.

Parameters for Population Effective Size and Mortality

Parametera	Females	Males	Both Sexes	Sex Ratio
Population effective size (% of initial cohort):
With children	42.3	38.4	40.3
With married children	34.6	32.7	33.7
With married female children	31.0	29.8	30.4
With married male children	29.8	28.8	29.3
Mortality:
Deaths at age 0–15 years (per 1,000)	323.5	362.7	343.7	1.22
Deaths at age 15–50 years (per 1,000)	215.5	141.2	176.8	.71
Deaths at age ⩾50 years (per 1,000)	461.0	496.1	479.5	1.17
Life expectancy at birth (years)	41.8	42.1	42.0
Life expectancy at age 15 years (years)	45.6	49.9	47.8

^aEffective size and mortality parameters are those of the 19th-century Saguenay cohorts (n=19,782).

Another factor influencing the intergenerational intervals is the average age at marriage. In societies where most of the children are born within wedlock, the higher the age at which people marry, the longer the intervals between generations. In the studied population, age at marriage was relatively low, compared with that in most European populations of the same period (Rallu and Blum 1991), meaning that for these latter populations, the average interval might be >30 years. In societies where marriage or some other ritual does not sanction entry into reproductive life, age at menarche must be used as the starting point of the fertility period. According to several studies, mean menarcheal age has been decreasing in many societies in the past hundred years (Rosenberg 1991; Tryggvadottir et al. 1994). It has also been shown that fertility is low in the initial years after menarche (Becker 1993; Riley et al. 1996). Therefore, children born to women <20 years old would not represent a large portion of all children.

In summary, our results may be more applicable to studies on populations covering a relatively recent period than to those going back to prehistoric times. Nevertheless, without any other reliable evidence on the length and evolution of intergenerational intervals in human populations, we suggest that the average value of 30 years per generation should be chosen instead of the usual 20 or 25 years.