A Two-Stage Variable-Stringency Semiparametric Method for Mapping Quantitative-Trait Loci with the Use of Genomewide-Scan Data on Sib Pairs

Abstract

Genomewide scans for mapping loci have proved to be extremely powerful and popular. We present a semiparametric method of mapping a quantitative-trait locus (QTL) or QTLs with the use of sib-pair data generated from a two-stage genomic scan. In a two-stage genomic scan, either the entire genome or a large portion of the genome is saturated with low-density markers at the first stage. At the second stage, the intervals that are identified as probable locations of the trait loci, by means of analysis of data from the first stage, are then saturated with higher-density markers. These data are then analyzed for fine mapping of the loci. Our statistical strategy for analysis of data from the first stage is a low-stringency method based on the rank correlation of squared trait-difference values of the sib pairs and the estimated identity-by-descent scores at the marker loci. We suggest the use of a low-stringency method at the first stage, to save on computational time and to avoid missing any marker interval that may contain the trait loci. For analysis of data from the second stage, we have developed a high-stringency nonparametric-regression approach, using the kernel-smoothing technique. Through extensive simulations, we show that this approach is more powerful than is a currently used method for mapping QTLs by use of sib pairs, particularly in the presence of dominance and epistatic effects at the trait loci.

Introduction

Genomewide scans are a powerful approach for mapping genes (Collins 1995; Lander and Kruglyak 1995), and they have already been proved successful (Elbein et al. 1999; Krushkal et al. 1999; Niu et al. 1999; Wyst et al. 1999). With the use of this approach, in addition to the collection of data on the trait/disease of interest, genotype data are generated on a large number of markers that are spread—preferably evenly—across the entire genome. Since the collection of pedigree data is difficult, a popular approach is to collect data on sib pairs and to analyze the data with the use of appropriate statistical techniques (Haseman and Elston 1972; Blackwelder and Elston 1985; Amos et al. 1989; Amos and Elston 1989; Lander and Botstein 1989; Goldgar 1990; Haley and Knott 1992; Jansen 1993; Olson and Wijsman 1993; Fulker and Cardon 1994; Olson 1995a, 1995b; Page et al. 1998; Alcais et al. 1999; Allison et al. 1999). Although, for qualitative traits in humans, various statistical methods—both parametric and nonparametric—have been proposed for linkage analysis and although their relative efficiencies have been extensively tested, such methods are still being developed (Olson 1995b; Almasy et al. 1998; Page et al. 1998; Alcais et al. 1999; Allison et al. 1999) and compared (Williams et al. 1999) for human quantitative traits. Parametric methods for mapping a QTL or QTLs involve parametric models, and, thus, they are susceptible to minor deviations in distributional assumptions. The nonparametric methods that are currently used (Haseman and Elston 1972; Kruglyak and Lander 1995a, 1995b) are relatively more robust, but they require specification of the trait model, and inferences based on the proposed statistics rely on asymptotic distributions. In this paper, we propose the use of a two-stage method for locating the most-likely position of a QTL on a chromosome, given trait values and marker-genotype trait values for a set of sib pairs. We first considered that the trait was being determined by a single QTL with environmental effects, and we then extended the proposed procedure to consider the possibility that the trait was being determined by multiple QTLs. When genomewide scans that involve a large number of markers are performed, a preferred strategy is to use a set of low-density markers (e.g., those at 5–10-cM intervals) to identify the region(s) in which the QTL(s) may be located and then to saturate these identified regions with high-density markers (e.g., those at 1–5-cM intervals) to fine map the QTL. This two-stage approach is cost-effective, both computationally and in terms of genotyping. Our proposed two-stage protocol is meant for analysis of sib-pair data generated in this manner. We have used variable stringencies in the two stages of our procedure. A low stringency is used in the first stage, to reduce the possibility of missing any marker interval that may contain the trait loci. At the second stage of fine mapping, we have used a higher stringency to reduce the probability of a false positive error. However, we note that the second stage of our procedure can also be directly used for analysis of sib-pair data, although the computational cost will be higher. In any case, from a study-design point of view, use of a two-stage strategy of data generation and analysis is logically more preferable than is use of a one-stage strategy. In the first stage, we identify the subset of markers that is linked to the QTL, by use of a test statistic based on rank correlation of estimated marker identity-by-descent (i.b.d.) scores and squared difference of sib-pair trait values. In the second stage, we perform nonparametric regression of the squared sib-pair trait difference on estimated i.b.d. scores for the different possible pairs of flanking markers, by use of kernel smoothing (Silverman 1986). We have denoted our procedure as being “semiparametric,” even though we have used nonparametric data-analytic procedures at both stages, because of certain underlying model parameters and assumptions (e.g., allele frequency and Hardy-Weinberg equilibrium). We have compared our semiparametric procedure with the parametric-regression procedure proposed by Olson (1995b) and have shown, by use of Monte-Carlo simulation, that, while the parametric method is marginally more efficient than is our semiparametric method, when there is no dominance effect at the trait locus (loci), the proposed method is much more efficient in the presence of dominance and/or epistasis.

Model

We assume that a quantitative trait Y is controlled by an autosomal biallelic locus with alleles A and a. The expectations of Y, conditional on the three genotypes AA, Aa, and aa, are assumed to be α, β, and −α, respectively. The variance of Y within each genotype is assumed to be equal, σ². No assumption is made regarding the shape of the probability distribution of the trait values. The underlying population is assumed to be in Hardy-Weinberg equilibrium with respect to the trait locus. We assume that the trait locus is in linkage equilibrium with a pair of autosomal, biallelic, codominant flanking marker loci.

Suppose that [(y_j1,y_j2):j=1,2,…,n] are the observed values of the quantitative trait of n independent sib pairs. We assume that the expectation of the correlation coefficient between the trait values of any sib pair is equal, ρ. Let π_j1,π_j2,…,π_jk denote the proportions of alleles shared i.b.d. at k ordered marker loci found on the same chromosome, for the jth sib pair. Let 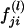denote the probability that the jth sib pair has i alleles shared i.b.d. at the lth marker locus, where i=0,1,2; l=1,2,…,k. Then, the estimator of π_jl is given by 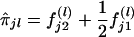; l=1,2,…,k. Haseman and Elston (1972) have explicitly calculated f^(l)_ji for different mating types, and, in the case of missing parental information, they have suggested an algorithm considering phenosets (Cotterman 1969).

Given data on the quantitative trait of the sib pairs and the estimated i.b.d. scores at the k ordered marker loci, our aim is to determine the most-likely interval in which the trait locus is found. We define y_j=(y_j1-y_j2)², j=1,2,…,n—that is, y_j denotes the squared pair difference in the trait values for the jth sib pair.

Coarse Mapping Based on Rank Correlation

The first step is to analyze data generated from a genomewide scan by use of coarsely spaced (at 5–10-cM intervals) markers and to test whether the trait locus shows any linkage to any of the k ordered marker loci considered. When a trait locus and a marker locus are linked, it is expected that siblings with similar trait values will exhibit considerable sharing of alleles at the marker locus. If the trait and the marker loci are unlinked, then, in spite of a significant sharing of alleles i.b.d. between a pair of siblings, their trait values may be largely dissimilar. Thus, a natural test for linkage between the trait locus and the lth marker locus (l=1,2,…,k) is a test for the strength of correlation between y_j's and 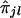's. A nonparametric technique of testing for no correlation between y_j's and 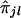's is based on Spearman rank correlation (see Randles and Wolfe 1979). Since 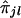can assume only five distinct values (i.e., 0, 1/4, 1/2, 3/4, and 1), it is expected that there will be many ties in 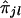values. Thus, we need to use the Spearman rank-correlation formula for the case of ties, which is as follows:

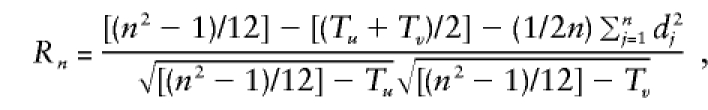where

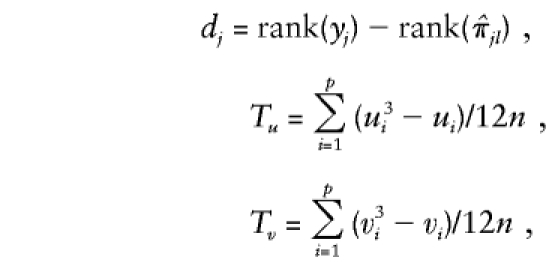with there being p ties in y_j's of lengths u₁,u₂,…,u_p and q ties in 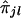's of lengths v₁,v₂,…,v_q.

The test statistic is 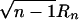, which is asymptotically distributed as N(0,1) under the null hypothesis of no correlation. Thus, for a level α test, the critical region is given by 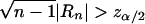, where z_m is the (1-m)th quantile of a standard normal variate. If the null hypothesis of no correlation is accepted for all the k marker loci (with the level of significance adjusted to α/k, to account for the multiple tests), then our conclusion is that the trait locus is most probably not located on the same chromosome as are the k marker loci.

Using the above test procedure, we selected those marker loci for which the null hypothesis of no correlation between y_j's and 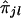's is rejected—that is, those marker loci that show evidence of linkage with the trait locus. In the next section, we will consider two such consecutive marker loci as candidate markers flanking the trait locus.

Fine Mapping Based on Nonparametric Regression

Since, at the first-stage of the genomewide scan, the marker spacing was coarse, the distance between the two markers found to provide the highest evidence of linkage (the highest value of the rank correlation) with the QTL is 5–10 cM. At the second stage, this genomic region/interval is covered with densely spaced markers, and the data thus generated are analyzed for the purpose of fine mapping of the QTL. Let us assume that this region/interval is covered with M densely spaced markers. Consider, without loss of generality, the ordered consecutive densely spaced markers 1 and 2. We propose a nonparametric additive regression model given by

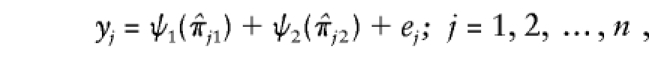where ψ₁ and ψ₂ are real-valued functions of 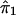and 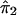, respectively, and where e_j's are random errors. The regression model is motivated by the fact that the estimated i.b.d. scores of siblings at both marker loci 1 and 2 were found to be individually significantly correlated with the squared difference of the trait values (y). However, the nature of dependence, on y_j, of the estimated i.b.d. scores 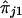and 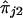is a function of the recombination distances between the marker and trait loci and other biological parameters, such as interference and dominance at the trait locus. Hence, we do not assume any specific form of the functions ψ₁ and ψ₂, but we do assume only general functional forms to model the nature of dependence between 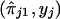and 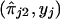. The functional forms are estimated from the data. Estimates of ψ₁ and ψ₂ are obtained in steps and iteratively, with use of kernel-smoothing techniques (see Silverman 1986). In this technique of nonparametric regression, the domains of the explanatory variables are divided into a number of windows. Local smoothing is done within each window, and appropriate adjustments are made to ensure continuity at window boundaries. In step 1, we perform a nonparametric-regression analysis of y on 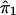(details will be given later) and obtain 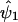, an estimate of ψ₁. In step 2, we replace y by 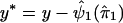. In step 3, we regress y^* on 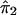to obtain 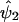, which is an estimate of ψ₂. In step 4, we compute the residual sum of squares given by 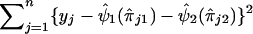. We then restart the process at step 1 and perform a regression analysis of 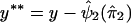on 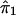. We continue to iterate until 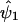and 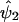stabilize reasonably—that is, the residual sum of squares differs negligibly (<ε, a small predetermined positive real number) in two successive iterations. The stringency parameter, ε, is obviously variable. Let the final residual sum of squares obtained be denoted by CV(1,2) and, in general, by CV(l,l+1), when the lth and (l+1)th marker loci are considered. The most-likely position of the trait locus is given by the interval flanked by the ith and (i+1)th marker loci, where i corresponds to

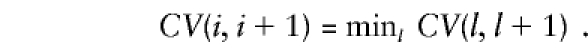To regress y on 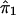, the range of 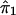is divided into windows of length h. The kernel function that is used is

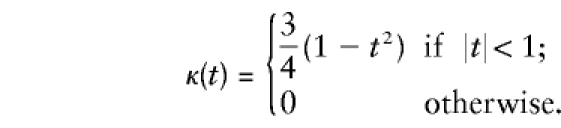The kernel estimator of ψ₁ is given as follows:

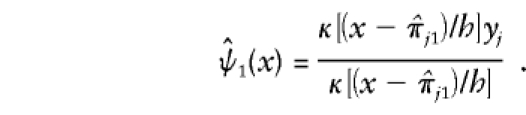Since nonparametric regression tends to overfit data (Silverman 1986), we use the “leave-one-out technique”—that is, we leave out the observation 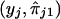in order to predict y_j. The predictor of y_j is given as follows:

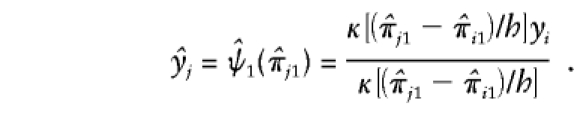For the given window length h, the total error in prediction is given by 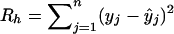. The process is repeated for different window lengths. The optimal window length h^* is given by that h for which R_h is minimum.

A Currently Used Linear-Regression Strategy

Suppose that A and a denote the alleles at the trait locus. Given the genotypes at the trait locus, let the conditional expectation, E(Y), of the quantitative character Y be α, 0, and −α for AA, Aa, and aa, respectively. If 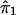and 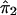denote the estimated i.b.d. scores at the two marker loci flanking the trait locus, Olson (1995b) showed that

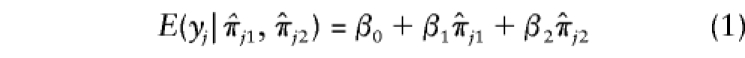for some constants β₀, β₁, and β₂.

Thus, a strategy for determination of the location of the trait locus is based on linear regression of y_j's on the i.b.d. scores of possible pairs of flanking markers. If the lth and (l+1)th marker loci are considered, then y_j is predicted by 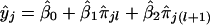, where 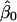, , 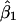and 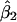are the least-squares estimators of β₀, β₁, and β₂ respectively. Tests for linkage are equivalent to tests of β₁ and β₂, which involve parametric-test statistics. The error sum of squares is given by 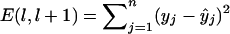. The most-likely interval of the trait-locus location is given by that flanked by the ith and (i+1) markers, if and only if

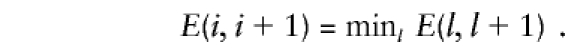Using Monte-Carlo simulations, we have examined the relative efficiencies of the proposed nonparametric procedure and the parametric method developed by Olson (1995b). In regression analysis, to avoid regressional overfits to data, it is statistically desirable to use the leave-one-out technique for prediction of y_j, which is what we have prescribed and have used for the proposed semiparametric-regression procedure. However, in Olson’s (1995b) parametric-regression procedure, this was not prescribed, and perhaps it is not used in practice. For purposes of comparing the proposed method with that of Olson (1995b), we have used the leave-one-out technique for both methods. We have also computed and compared the error sum of squares without use of the leave-one-out technique for Olson’s (1995b) method, although such comparisons are not strictly valid, because it is expected a priori that the error sum of squares obtained without use of the leave-one-out technique will be smaller than that which will be obtained with use of the leave-one-out technique, in view of overfitting.

We note that equation (1) is valid only when there is no dominance at the trait locus. When there is dominance, the conditional expectation on the left-hand side of equation (1) is not a linear function of 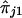and 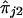. Hence, use of the linear regression given in equation (1) may yield incorrect inferences.

Simulation

To assess the performance of our proposed nonparametric-regression strategy and to compare it with the parametric-regression strategy described in the A Currently Used Linear-Regression Strategy section, we have generated data on trait values of sib pairs and have estimated marker i.b.d. scores for different sets of parameter values. The different steps of the simulation algorithm are described below. In the first step, we generated the trait i.b.d. scores of sib pairs by use of a trinomial random-number generator with cell probabilities of  1/4,  1/2, and  1/4, respectively. In the second step, we generated the trait genotypes of the sib pairs from a multinomial distribution, with cell probabilities given by the conditional probabilities of the generated trait i.b.d scores, given the trait-genotypic pair (given in table 1 of the study by Haseman and Elston [1972]). In the third step, we generated the trait values of the sib pairs from a bivariate normal distribution with appropriate mean vector and covariance matrix, depending on the trait genotypes of the sib pair, as described in the Model section above. In the fourth step, we obtained the squared difference of the trait values of each sib pair. In the fifth step, we generated the i.b.d. scores of the sib pairs for each of the two markers flanking the trait locus, conditional on the generated trait i.b.d. scores from a trinomial distribution (given in table 4 of the study by Haseman and Elston [1972]). In the sixth step, we sequentially generated the i.b.d. scores of the sib pairs for each nonflanking marker, conditional on the generated i.b.d. score of the marker flanking it, from the same trinomial distribution used in the previous step. In the seventh step, we generated the estimated i.b.d. scores of the sib pairs for each of the markers, conditional on the generated marker i.b.d. scores from a 5-nomial distribution (given in table 5 of the study by Haseman and Elston [1972]).

Having generated the required data on n independent sib pairs, we used the proposed test of linkage based on rank correlation to select the possible pairs of flanking markers. We then performed both the nonparametric and parametric regressions to determine the most-likely position of the trait locus. For the nonparametric regression, the stringency parameter ε was kept fixed at .001.

Results

In this section, we denote the trait parameters as follows:

• 1. Effect of the genotype AA on trait values = α.
• 2. Dominance effect of the trait locus = β.
• 3. Frequency of allele A=p.
• 4. Variance of the trait values within any trait genotype = σ².
• 5. Correlation coefficient between the trait values of any sib pair = ρ

Identification of the Probable Interval Locations of the QTL

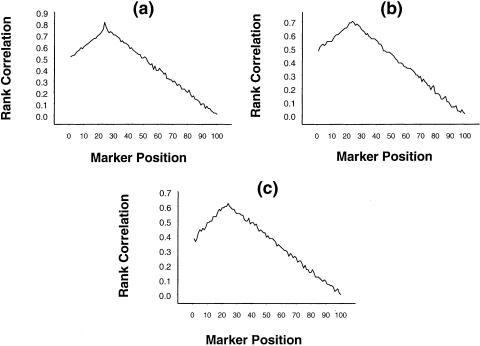
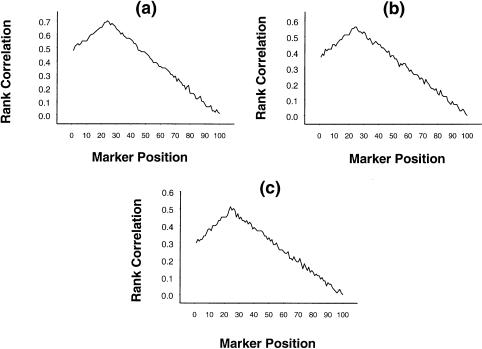
To assess the performance of the rank-correlation statistic in the identification of the interval location of the QTL, we have generated data on 100 ordered, equally spaced markers, such that the recombination fraction between any two consecutive markers is .05. Simulated data were generated under the assumptions that the trait locus is flanked by the 24th and 25th markers and that the recombination fraction between the trait locus and the 24th marker is .02. The trait parameter values used in the simulation were α=5; β=0, 2, or 4; p=.7; σ²=1; and ρ=.6 (or higher). The nature of the absolute rank correlation between the different markers and the squared difference in trait values of the sib pairs is presented in figure 1a–c, for β=0, 2, and 4, respectively. From the figures, we find that the absolute rank correlation increases with the proximity of the considered marker to the trait locus. The peak was at the 24th marker, correctly indicating the approximate location of the trait locus. Though with increase in β (i.e., the dominance effect) the peak becomes less pronounced, the approximate position of the trait locus is fairly clear, even for a high-dominance effect.

Figure 1.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers, with the use of simulation parameter values α=5, σ²=1, p=.7, ρ=.6, and (a) β=0, (b) β=2, and (c) β=4, on the basis of data from 100 sib pairs.

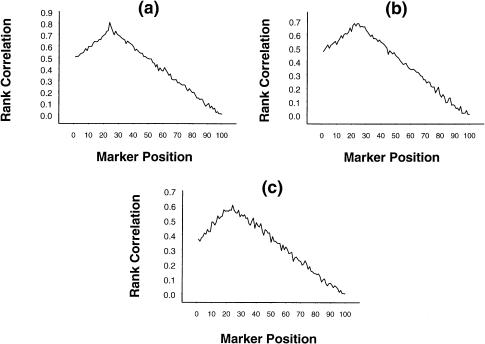
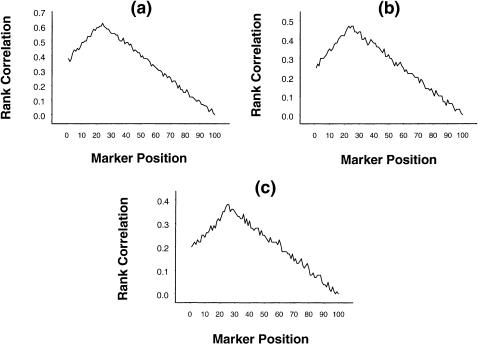
To investigate the effect of changing α, we present, in figure 2a–c, graphs that are similar to those in figure 1a–c but that have α=3 and β=0, 1, and 2, respectively. As is evident from these figures, although the mean values of the rank correlation became slightly smaller, the nature of the graphs and, hence, the qualitative inferences remained unchanged.

Figure 2.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers, with the use of simulation parameter values α=3, σ²=1, p=.7, ρ=.6, and (a) β=0, (b) β=1, and (c) β=2, on the basis of data from 100 sib pairs.

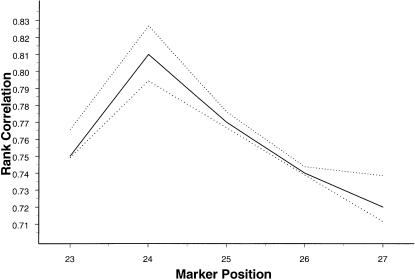
The variation in the values of the rank correlation across the 1,000 simulation replications was extremely small for every set of parameter values. We present, in figure 3, the empirical 95% confidence band for a section of the graph presented in figure 1a. (The empirical confidence bands were so narrow that these are not clearly presentable in figure 1a–c.) This indicates another desirable statistical property of the proposed method.

Figure 3.

Both the mean rank correlation (unbroken line), based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at markers around the true QTL location, and the empirical 95% confidence band (dotted lines) for simulation parameter values α=5, β=0, σ²=1, p=.7, and ρ=.6.

Finer Localization of the QTL

Once the interval in which the QTL may be located has been identified, then, in practice, one saturates this interval with more-dense markers, to arrive at a finer localization of the QTL. To simulate this practice, we consider data on multiple markers that are more densely located within the coarse interval identified at the previous stage. In our simulations, we generated data on a set of M ordered markers. We used the following notations:

• 1. The recombination fractions between the trait locus and the nearest flanking markers 2 and 3, are θ₂ and θ₃, respectively.
• 2. The recombination fraction between markers 1 and 2 is θ₁.
• 3. The recombination fraction between markers 3 and 4 is θ₄.
• 4. The recombination fraction between markers 4 and 5 is θ₅.

We have used simulation parameter values of M=5; α=5; σ²=1; θ₁=θ₂=θ₃=θ₄=θ₅=.01; β=0, 2, and 4; and different parameter values of p and ρ, such that the proportion of variance in the trait explained by the QTL varied between 85%–95 %. For each set of parameter values, we have performed 1,000 iterations. The results are given in table 1. In all the cases, the five markers were found to be linked to the trait locus at the 1% level of significance. Thus, we have four candidate intervals (i.e., those flanked by markers 1 and 2, 2 and 3, 3 and 4, and 4 and 5) in which the trait locus may be located.

Table 1.

Comparison of Nonparametric and Parametric Regressions, Based on Average Prediction Error (Residual Sums of Squares Averaged Over 1,000 Replications), for a Single QTL, with 100 Sib Pairs^[Note]

Candidate Interval	Error in Predictiona
	NP (97.2%)	P1 (98.5%)	P2 (98.9%)
β = 0, p = .5, ρ = .8:
(1,2)	100.56	95.46	92.71
(2,3)	87.65	74.72	70.62
(3,4)	104.29	99.55	97.68
(4,5)	117.03	110.84	107.27
	NP (90.7%)	P1 (82.5%)	P2 (84.1%)
β = 2, p = .9, ρ = .7:
(1,2)	152.76	157.63	155.35
(2,3)	143.37	148.54	146.72
(3,4)	152.90	160.81	157.64
(4,5)	166.29	173.06	171.18
	NP (75.8%)	P1 (43.0%)	P2 (51.5%)
β = 4, p = .7, ρ = .5:
(1,2)	182.45	196.74	193.27
(2,3)	180.34	194.68	191.93
(3,4)	185.74	194.52	193.22
(4,5)	190.59	207.02	203.51

Note.—Simulation parameter values were α=5, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01.

^aNP = nonparametric regression; P1 = parametric regression with the leave-one-out technique; P2 = parametric regression without the leave-one-out technique (i.e., standard parametric regression). Results in parentheses denote the percentages of correct identification of the true interval location.

When β=0 (i.e., there is no dominance effect), equation (1) holds. Thus, it is expected that the parametric approach will be more efficient. We find that, in almost all replications, both of the methods correctly identify the interval in which the QTL is located. Although the parametric regression has a smaller error in prediction, the error in the nonparametric regression is not much larger. The error in prediction is lowest for the parametric regression without use of the leave-one-out technique (P2). As mentioned earlier, this is not unexpected, since, without use of the leave-one-out technique, there is obvious overfitting of the regression model to the data. Since we have, therefore, recommended and used the leave-one-out technique, the apropriate comparison of prediction errors with the proposed nonparametric approach and the parametric approach should be between columns NP and P1. (P2 is presented for completeness, since the leave-one-out technique may not be used in practice—even though it should be used to avoid false inferences from model overfits.) When β=2 or 4, equation (1) does not hold. In the presence of dominance, whereas the nonparametric approach identifies the correct interval in 91% of the cases when β=2, the parametric approach does so in only 83%–84% of the cases. The nonparametric approach has a smaller error in prediction. When β=4 (i.e., when there is a high-dominance effect), the performance of the parametric approach is very poor compared with that of the nonparametric approach. Although with use of parametric regression the percentage of correct identification of the interval is only 43%–51%, the percentage obtained with use of the nonparametric regression is 76%. Under this scenario, the average prediction error is also much higher for the parametric-regression method, compared with the nonparametric-regression method. Thus, we find that, while the nonparametric approach performs almost as efficiently as does the parametric approach when there is no dominance effect, it performs increasingly better than does the parametric approach, as the dominance effect increases.

We have also investigated the effect of changing the values of the parameters α and β. In table 2, we present results similar to those seen in table 1 but with α=3 and β=0, 1, and 2. Qualitatively, the inferences are similar to those derived from table 1; in the absence of dominance, the parametric regression performs better than does the nonparametric regression, but the converse is true in the presence of dominance. We find that, in table 2, the percentages of correct identification are lower and the prediction errors are higher than those in table 1. This is because the proportion of trait variance explained by the QTL is a function of α and β in addition to other parameters; this proportion decreases with reduction in α for fixed values of β and other parameters. In other words, there is a decrease in the efficiencies of performance, both for nonparametric and parametric procedures, as the proportion of trait variance explained by the QTL decreases.

Table 2.

Comparison of Nonparametric and Parametric Regressions, Based on Average Prediction Error (Residual Sums of Squares Averaged Over 1,000 Replications), for a Single QTL, with 100 Sib Pairs ^[Note]

Candidate Interval	Error in Predictiona
	NP (95.2%)	P1 (97.0%)	P2 (97.8%)
β = 0, p = .5, ρ = .8:
(1,2)	104.72	98.44	95.61
(2,3)	92.83	78.69	74.25
(3,4)	106.29	101.54	99.02
(4,5)	122.18	114.84	110.49
	NP (88.4%)	P1 (80.6%)	P2 (82.9%)
β = 1, p = .9, ρ = .7:
(1,2)	162.26	167.05	165.11
(2,3)	147.75	154.68	151.83
(3,4)	164.90	168.32	165.17
(4,5)	179.44	188.69	184.72
	NP (71.5%)	P1 (40.4%)	P2 (43.7%)
β = 2, p = .7, ρ = .5:
(1,2)	196.65	211.76	203.38
(2,3)	188.07	200.55	197.63
(3,4)	199.19	213.01	206.05
(4,5)	212.92	225.47	218.86

Note.—Simulation parameter values were α=3, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01.

^aDefinitions of abbreviations and results in parentheses are the same as those given in table 1.

We have likewise investigated the effect of changes in trait-allele frequencies, for fixed values of α, β, and other parameters. The results are presented in table 3. We find that, as p deviates from .5 (for fixed values of the other parameters), the percentage of correct identification of the interval decreases and the error in prediction increases both for nonparametric- and parametric-regression methods. As was explained in the preceding paragraph, this is not unexpected, because, for fixed values of the other parameters, the proportion of trait variance explained by the QTL decreases as p deviates from .5. With dominance, the nonparametric method performs better than does the parametric method, for all values of the trait-allele frequency.

Table 3.

Comparison of Nonparametric and Parametric Regressions, Based onAverage Prediction Error (Residual Sums of Squares Averaged over 1,000 Replications) for Different Allele Frequencies of the QTL, for a Single QTL, with 100 Sib Pairs^[Note]

Candidate Interval	Error in Predictiona
	NP (90.7%)	P1 (82.5%)	P2 (84.1%)
p = .9:
(1,2)	152.76	157.63	155.35
(2,3)	143.37	148.54	146.72
(3,4)	152.90	160.81	157.64
(4,5)	166.29	173.06	171.18
	NP (92.7%)	P1 (85.3%)	P2 (87.8%)
p = .7:
(1,2)	146.52	153.67	150.29
(2,3)	135.44	143.48	140.03
(3,4)	150.41	155.13	152.45
(4,5)	166.22	176.52	171.38
	NP (94.5%)	P1 (87.0%)	P2 (89.7%)
p = .5:
(1,2)	139.80	146.26	142.97
(2,3)	123.04	137.51	131.58
(3,4)	141.36	150.75	144.84
(4,5)	157.59	168.22	164.17

Note.—Simulation parameter values were α=5, β=2, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01.

^aDefinitions of abbreviations and results in parentheses are the same as those given in table 1.

Assessment of Type I Error

To determine the efficacy of a statistical procedure, it is imperative that the type I error rate be assessed. In the present context, the probability of type I error is the probability of rejection of the null hypothesis of no linkage between the QTL and any of the markers considered, when, actually, the QTL is unlinked to the markers. To assess this, we generated the trait values from the underlying distribution, the details of which have been provided in the Model section above. The sib-pair i.b.d. scores at the various marker loci were generated from a trinomial distribution, independent of the trait i.b.d. scores. This ensured that the QTL was unlinked to any of the markers considered. Such data were generated for 100 sib pairs for each replication; 1,000 replications were performed.

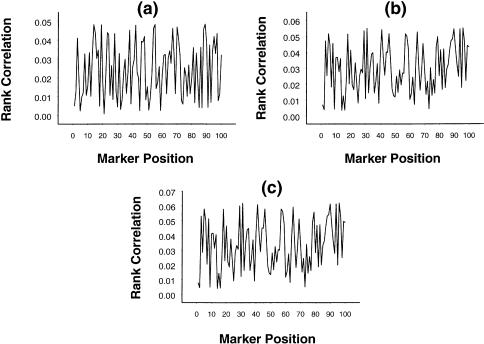
These data were then analyzed with use of the rank-correlation statistic, as is prescribed for the first stage of the proposed two-stage procedure. For the set of 100 ordered markers, the values of the rank correlation, averaged over 1,000 replications, are graphically presented in figure 4. The mean rank-correlation values were all small and were statistically nonsignificant. This inference holds at all levels of dominance at the trait locus. Thus, the empirical estimate of the type I error probability is zero. In practice, a fine-mapping protocol is undertaken only when some “probable” intervals are identified, at the first stage, on the basis of statistically significant values of the rank correlation. However, in the present case, there was no need for further investigation, since the null hypothesis was accepted for all the markers considered.

Figure 4.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers (all of which were unlinked to the QTL), with the use of simulation parameter values α=5, σ²=1, p=.7, ρ=.6, and (a) β=0, (b) β=2, and (c) β=4, on the basis of data from 100 sib pairs.

Effect of Sample Size

To assess the effect of reduction of the sample size on the proposed procedure, we simulated the required data on samples of 50 and 25 sib pairs with varying dominance effect on the trait. The nature of the absolute rank correlations between the trait value and the estimated i.b.d. scores at the 100 generated markers is presented in figures 5a–c and 6a–c, for sample sizes of 50 and 25 sib pairs, respectively. Compared with the rank correlations based on 100 sib pairs [see fig. 1a–c], these rank correlations, in general, decrease with a decrease in the sample size. However, the peak at the 24th marker is prominent, even with the use of 25 sib pairs. Thus, the approximate position of the trait locus is indicated correctly even for small sample sizes. The effect of dominance on the rank correlations is identical to that seen for 100 sib pairs, as discussed in the Finer Localization of the QTL section.

Figure 5.

Mean rank correlation, based on 1, 000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers, with the use of simulation parameter values α=5, σ²=1, p=.7, ρ=.6, and (a) β=0, (b) β=2, and (c) β=4, on the basis of data from 50 sib pairs.

Figure 6.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers, with the use of simulation parameter values α=5, σ²=1, p=.7, ρ=.6, and (a) β=0, (b) β=2, and (c) β=4, on the basis of data from 25 sib pairs.

We repeated the nonparametric regression with the use of samples of 50 and 25 sib pairs, using the same set of parameter values and five markers that we had previously used. The results are presented in tables 4 and 5, respectively. We found that the percentage of correct identification of flanking markers decreases with a decrease in sample size, for both the parametric- and the nonparametric-regression procedures. The rate of decrease is greater when the dominance effect is high (i.e., β=4). As was observed with the use of 100 sib pairs, we found that, with the use of smaller sample sizes, while the performance of the nonparametric-regression approach is similar to that of the parametric-regression approach when there is no dominance effect, the performance of the nonparametric-regression procedure is significantly better when the degree of dominance in the trait is high. Furthermore, the nonparametric method performs increasingly better with decreasing sample size, in the presence of dominance effects.

Table 4.

Comparison of Nonparametric and Parametric Regressions, Based on Average Prediction Error (Residual Sums of Squares Averaged over 1,000 Replications), for a Single QTL, With 50 Sib Pairs^[Note]

Candidate Interval	Error in Predictiona
	NP (95.3%)	P1 (97.6%)	P2 (98.0%)
β = 0, p = .5, ρ = .8:
(1,2)	111.45	107.56	104.87
(2,3)	103.40	100.48	97.84
(3,4)	112.83	109.58	105.53
(4,5)	122.17	118.97	116.04
	NP (84.7%)	P1 (80.2%)	P2 (81.3%)
β = 2, p = .9, ρ = .7:
(1,2)	167.93	170.56	168.01
(2,3)	160.26	165.02	161.36
(3,4)	169.88	172.64	169.90
(4,5)	184.71	191.39	188.55
	NP (70.7%)	P1 (38.8%)	P2 (40.7%)
β = 4, p = .7, ρ = .5:
(1,2)	212.68	216.44	214.85
(2,3)	207.79	215.75	210.26
(3,4)	210.92	214.50	213.13
(4,5)	221.36	229.23	226.39

Note.—Simulation parameter values were α=5, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01.

^aDefinitions of abbreviations and results in parentheses are the same as those given in table 1.

Table 5.

Comparison of Nonparametric and Parametric Regressions, Based on Average Prediction Error (Residual Sums of Squares Averaged over 1,000 Replications), for a Single QTL, with 25 Sib Pairs^[Note]

Candidate Interval	Error in Predictiona
	NP (93.1%)	P1 (95.4%)	P2 (96.2%)
β = 0, p = .5, ρ = .8:
(1,2)	126.04	122.76	119.64
(2,3)	118.48	115.57	112.05
(3,4)	128.16	121.35	120.03
(4,5)	143.74	137.43	134.68
	NP (82.6%)	P1 (75.3%)	P2 (77.0%)
β = 2, p = .9, ρ = .7:
(1,2)	171.28	176.55	174.16
(2,3)	164.09	171.63	167.32
(3,4)	173.37	178.80	175.09
(4,5)	188.48	198.06	195.45
	NP (65.5%)	P1 (34.2%)	P2 (35.9%)
β = 4, p = .7, ρ = .5:
(1,2)	229.53	240.08	237.62
(2,3)	220.49	238.16	233.44
(3,4)	226.86	237.61	233.38
(4,5)	243.35	258.77	255.26

Note.— Simulation parameter values were α=5, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01.

^aDefinitions of abbreviations and results in parentheses are the same as those given in table 1.

Effect of Deviation from Normality

Nonparametric statistical procedures are usually less sensitive to minor deviations in distributional assumptions. Both the linear-regression procedure (Olson 1995b) and the nonparametric-regression procedure proposed here are expected to be robust with respect to the underlying trait distribution of the sib pairs. We note that the test procedure used in Olson’s method (1995b) is based on distributional assumptions. Thus, it is of considerable interest to assess the performance of both of the procedures when there is deviation from the assumed trait distribution. One of the existing methods of evaluating the effect of deviation is to introduce local perturbations in the original distribution. In our previous simulation examples, we had generated the trait values of the sib pairs from a bivariate normal distribution. To assess the effect of the trait distribution deviating from normal on the identification of the location of the interval of the QTL, we perturbed the relevant bivariate normal distributions with an exponential distribution with a mean of 1. To preserve the original mean vector and dispersion matrix of (y_i1,y_i2)'s (i.e., α=5, σ²=1, ρ=.7, and β=0, 2, 4), suitable shifts in location were made. We have considered two different perturbations with different intensities. In the first case, we considered a mixture of 80% of the original bivariate normal distribution and 20% of the exponential distribution with a mean of 1. In the second case, the mixture comprised 50% of each of the distributions mentioned above. With the other parameters (i.e., recombination fractions) remaining the same, we performed both the nonparametric and parametric regressions to identify the most-likely position of the QTL. The results with regard to the percentages of correct identification of flanking interval are given in table 6. When these percentages are compared with those presented in table 1, we find that perturbation added to the normal distribution has a very marginal effect on the ability to correctly identify the QTL-interval location, even when the amount of perturbation is as high as 50%. As was seen in the previous cases, although the nonparametric-regression procedure performs almost as well as does the parametric-regression procedure when there is no dominance, it performs increasingly more efficiently as the dominance effect increases.

Table 6.

Comparison of Nonparametric and Parametric Regressions, for a Single QTL, When the Trait Distribution Is Perturbed with Exponential Distribution^[Note]

		Percentage (%) of Correct Identification of True Interval Location ata
		20% Perturbation			50% Perturbation
Degree of Dominance   (β)		NP	P1	P2	NP	P1	P2
0	.5	95.1	98.3	98.9	94.8	98.1	98.6
2	.9	91.2	81.7	83.2	88.0	81.3	84.0
4	.7	73.6	48.5	50.6	71.7	46.4	48.8

Note.—Simulation parameter values were α=5, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01, ρ=.7.

^aDefinitions of abbreviations are the same as those given in table 1.

Detection of Multiple QTLs

When the trait is controlled by multiple loci, the proposed procedure for detection of a QTL with the use of flanking markers can be easily extended. Suppose that the quantitative trait is determined by two biallelic trait loci (A,a) and (B,b). Let the marginal expectations of trait values for individuals with genotypes AA, Aa, and aa be α₁, β₁, and −α₁, respectively, and let those for individuals with genotypes BB, Bb, and bb be α₂, β₂, and −α₂, respectively. We assume the conditional expectation of the trait, given that the genotypes at the two QTLs are additive. Thus, for example, the expected trait value for an individual with the genotype AABB is α₁+α₂; for an individual with the genotype Aabb, it is β₁-α₂; etc. For ease of exposition and simulation, we assume that the unlinked QTLs are actually on different chromosomes. Furthermore, the QTL are separately assumed to be in linkage equilibrium with a pair of flanking markers. On the basis of the data on trait values of n independent sib pairs and the estimated i.b.d. scores of two sets of ordered markers on two different chromosomes, our aim is to detect both of the QTLs by means of identification of the closest pair of flanking markers on each chromosome. Using the rank-correlation statistic, we can identify the possible pairs of candidate flanking markers on each chromosome and then can invoke either the parametric- or the nonparametric-regression procedure, to select the most-likely intervals where the two QTL are located.

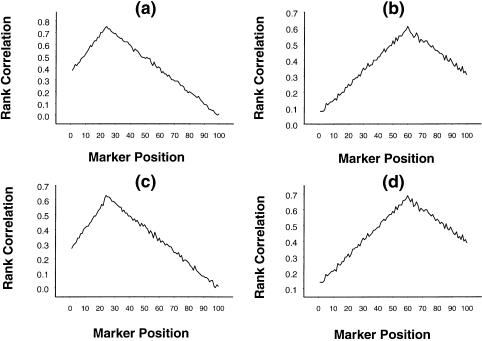
We have performed simulations to assess the performance of the rank-correlation statistic when there are two QTLs and to compare the performance of the parametric- and the nonparametric-regression procedures with regard to correctly locating the flanking intervals. To study the nature of rank correlations, we have generated data on 100 sib pairs, as described previously. We considered 100 ordered markers on each of the two chromosomes, with the recombination fraction between successive markers equal to .05. The first QTL is assumed to be located between the 24th and 25th markers on the first chromosome, and the second QTL is assumed to be located between the 60th and 61st markers on the second chromosome. Two sets of trait parameter values were chosen for generation of simulated data. In both sets, α₁ was chosen to be 5, and the other parameters were chosen such that, in the first case, there was no dominance at either QTL and the first QTL explained the trait variance of 80%, whereas, in the second case, there was a dominance effect only at the first QTL, and it explained the trait variance of 60%. The nature of the rank correlations is presented in figure 7a–d. Although the magnitudes of the rank correlations are, in general, less than those seen in the case of a single QTL, we find that, in both cases, peaks are prominent at the 24th marker on the first chromosome and at the 60th marker on the second chromosome, thus correctly identifying the approximate positions of the QTLs.

Figure 7.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers. Panels a and b pertain to the first and second loci, respectively, when the first locus, without dominance, explains 80% of the variation in trait values; panels c and d pertain to the first and second loci, respectively, when the first locus, with dominance, explains 60% of the variation in trait values.

To compare the parametric- and nonparametric-regression strategies in the case of two QTLs, we have generated data on five markers on each of the two chromosomes. The two sets of simulation trait parameter values were chosen as mentioned in the preceding paragraph. The percentages of correct identification of flanking markers on each chromosome are given in table 7. We find that, in the first case, where there is no dominance effect at either QTL, the percentage of correct identification of both QTLs is, as expected, slightly higher in the parametric procedure. However, the percentage of correct identification of both QTLs by means of the nonparametric procedure is as high as 93.2%, and, for all practical purposes, it is almost as efficient as the parametric procedure. In the second case, where there is dominance at the major QTL, the percentage of the correct identification of both of the QTLs is substantially higher (88.2%) with use of the nonparametric procedure. While the parametric procedure locates the second QTL (which has no dominance effect) in ∼90% of the simulation replications, the first QTL is correctly located in only 61%–73% of the replications. The corresponding figures for the nonparametric procedure are 92% and 87.5%, respectively. Thus, we find that the nonparametric procedure performs more efficiently, even when there is dominance in one of the two QTLs. We note that, in our simulations, whenever the flanking interval has been incorrectly identified, the QTL has been identified in an adjacent interval. Thus, the error in identification may not be of any major practical consequence. We also note that, for given values of the proportions of trait variance explained by the QTLs, there may be several possible combinations of trait parameter values (α's, β's, and p's). An obvious question is whether the performance of the procedures differs for such different combinations of trait parameter values that correspond to the same proportions of trait variance explained by the QTLs. We have investigated this problem and have found that different trait parameter values that conform to the same proportion of variance explained by the major QTL yield almost identical results, in terms of percentage of correct identification of the location of the interval.

Table 7.

Comparison of Nonparametric and Parametric Regressions, for Two QTLs, in the Absence of Epistasis and with 100 Sib Pairs^[Note]

	Percentagea of
Type of Identification (First QTL/Second QTL)	NP	P1	P2
No dominance effect at either QTLb:
Correct/correct	93.2	96.5	97.4
Correct/incorrect	6.8	3.5	2.6
Incorrect/correct	0	0	0
Incorrect/incorrect	0	0	0
Dominance effect at the first QTLc:
Correct/correct	82.2	65.7	69.6
Correct/incorrect	5.3	3.0	3.4
Incorrect/correct	9.8	23.6	21.8
Incorrect/incorrect	2.5	6.7	5.2

Note.—Simulation parameter values were α=5, σ²=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01, and there were 1,000 replications.

^aDefinitions of abbreviations are the same as those given in table 1.

^bTrait variance of 80% was explained by the first QTL.

^cTrait variance of 60% was explained by the first QTL.

We have previously ignored the possibility of epistatic interactions between the two QTLs. Epistatic interactions can be parametrized in a multitude of ways (Kearsey and Pooni 1996). However, to perform some preliminary investigations of the effect of epistatic interactions on the performance of the proposed method, we have considered a specific model of epistasis. This model is prompted by experimental observations in nonhuman organisms, and it has been denoted as the “digenic interaction model” (Kearsey and Pooni 1996). Under this model, the expectations of the trait value remain the same as before, for individuals who are not double homozygotes. For individuals who are double homozygotes, the expectations are as follows: E(Y|AABB)=α₁+α₂+Δ, E(Y|AAbb)=α₁-α₂-Δ, E(Y|aaBB)=-α₁+α₂-Δ, and E(Y|aabb)=-α₁-α₂+Δ. (The symbol Δ is variable for the different double homozygotes, to keep the marginal expectations unaltered.)

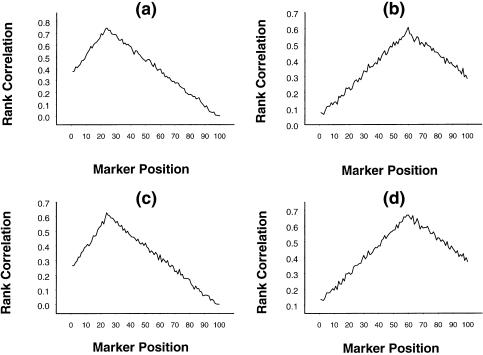
Under this digenic interaction model, simulated data were generated as described previously. The results of the first stage of our procedure are graphically depicted in figure 8a–d, with Δ=1, α₁=5, and other sets of parameter values chosen such that the first locus without any dominance effect explained 80% [fig. 8a and b] and such that the first locus with dominance effect explained 60% [fig. 8c and d] of the total variation in Y. It was observed that, in the presence of epistatic interaction, the magnitudes of the rank correlations are slightly lower than they are in the absence of epistatic interaction. The peaks are pronounced at the right locations of the QTLs. The results of the second stage of the proposed procedure are provided in table 8, and they show that the qualitative inferences are identical to those developed in the absence of epistasis; however, the percentages of correct identification of the interval are marginally lower. Thus, it is clear that the proposed procedure performs well at both stages, even in the presence of reasonable levels of epistatic interaction between the QTLs.

Figure 8.

Mean rank correlation, based on 1,000 replications, between squared difference of trait values of a sib pair and estimated i.b.d. scores at 100 ordered markers. Panels a and b pertain to the first and second loci, respectively, when the first locus, without dominance but with epistatic interaction with the second locus, explains 80% of the variation in trait values; panels c and d pertain to the first and second loci, respectively, when the first locus, with dominance and with epistatic interaction with the second locus, explains 60% of the variation in trait values.

Table 8.

Comparison of Nonparametric and Parametric Regressions, for Two QTLs, in the Presence of Epistasis and with 100 Sib Pairs^[Note]

	Percentagea of
Type of Identification (First QTL/Second QTL)	NP	P1	P2
No dominance effect at either QTLb:
Correct/correct	91.4	94.5	95.6
Correct/incorrect	8.6	5.5	4.4
Incorrect/correct	0	0	0
Incorrect/Incorrect	0	0	0
Dominance effect at the first QTLc:
Correct/correct	78.1	60.8	64.8
Correct/incorrect	6.5	3.3	4.9
Incorrect/correct	12.3	26.4	23.0
Incorrect/incorrect	3.1	9.5	7.3

Note.—Simulation parameter values were α=5, σ²=1, Δ=1, and θ₁=θ₂=θ₃=θ₄=θ₅=.01, and there were 1,000 replications.

^aDefinitions of abbreviations are the same as those given in table 1.

^bTrait variance of 80% was explained by the first QTL.

^cTrait variance of 60% was explained by the first QTL.

Discussion

Recent developments in molecular genetics have resulted in the increasing use of genomewide scans for mapping of traits. Genomewide scans yield huge data sets that require analyses with the use of efficient and robust statistical methods. In this paper, we have proposed a semiparametric strategy for QTL-interval mapping. Given the trait values of the sib pairs and the estimated i.b.d. scores of a set of ordered markers on a chromosome, we have developed a two-stage multipoint linkage method. We first reduce the data on markers, to include only those markers that provide indications of linkage (coarse mapping) to the QTL, using rank correlation. Then, we fine map the QTL. The two-stage approach was prompted by cost-benefit considerations of genotypic-data generation and statistical analyses. Although the adoption of a set of high-density markers in genomewide scans may provide maximal information, it is often prohibitively expensive. A statistically and logically more sound—as well as cost-effective—strategy is to initially use low-density markers (at, perhaps, 5–10-cM intervals) and to identify a set of probable marker intervals in which the QTL(s) may be located. Then, one can saturate these “probable intervals” with higher-density markers (i.e., those at 1–5-cM intervals) and can localize the QTL(s) to finer intervals. In fact, such a strategy has recently been adopted in a sib-pair linkage study of schizophrenia (Williams et al. 1999). The investigators performed a two-stage genomewide scan. In the first stage, the average density of the markers used was 17.26 cM. In the second stage, the intervals identified in stage 1 were saturated with markers with an average density of 5–10 cM. The proposed protocol uses a computationally easy, low-stringency, statistical criterion based on rank correlation, for analysis of low-density-marker data on sib pairs. For analysis of high-density-marker data—that is, for fine mapping—we have proposed a method that is capable of identifying even small “signals” of linkage evidence, because it does not use assumed functional forms for the nature of dependence between squared difference of sib-pair trait values and estimated i.b.d. scores. In fact, in the presence of dominance effects at the trait loci, which may be the rule rather than the exception, functional forms are difficult to derive algebraically. Furthermore, since local smoothing is performed, the efficiency of detecting evidence of linkage in small marker intervals is higher, and variations in values of trait parameters keeping the proportion of trait variance are explained by the QTL(s) at the same level. We have compared the proposed procedure with a currently used parametric-regression procedure (Olson 1995b) and have shown that the efficiency of our procedure in correctly identifying the interval locations increases with an increase in the degree of dominance at the trait locus. Moreover, with the use of the proposed procedure, the percentage of correct identification of flanking markers is not significantly adversely affected with reasonable reductions in sample sizes. We have also shown that the procedure is robust with respect to distributional assumptions.

We emphasize that, if one wishes to perform a one-step genome scan, the data can be analyzed with the use of either the proposed procedure based on rank correlation (which is computationally cheap) or nonparametric regression (which is computationally more expensive). A major advantage of the proposed procedure is that, unlike parametric-linkage methods, it does not involve modeling of epistasis and other trait parameters and, hence, is much more robust with respect to distributional assumptions.