Abstract
Family-based association methods have recently been introduced that allow testing for linkage in the presence of linkage disequilibrium between a marker and a disease even if there is only incomplete parental-marker information. No such tests are currently available for X-linked markers. This report fills this methodological gap by presenting the X-linked sibling transmission/disequilibrium test (XS-TDT) and the X-linked reconstruction-combination transmission/disequilibrium test (XRC-TDT). As do their autosomal counterparts (S-TDT and RC-TDT), these tests make no assumption about the mode of inheritance of the disease and the ascertainment of the sample. They protect against spurious association due to population stratification. The two tests were compared by simulations, which show that (1) the X-linked RC-TDT is, in general, considerably more powerful than the X-linked S-TDT and (2) the lack of parental-genotype information can be offset by the typing of a sufficient number of sibling controls. A freely available SAS implementation of these tests allows the calculation of exact P values.
A serious limitation of the transmission/disequilibrium test (TDT), introduced by Spielman et al. (1993), is that it requires genotype information on both parents, which may be difficult to obtain when the disease of interest has a late age at onset. Therefore, several methods have been proposed recently (Curtis 1997; Boehnke and Langefeld 1998; Horvath and Laird 1998; Schaid and Rowland 1998; Spielman and Ewens 1998; Knapp 1999a; Rabinowitz and Laird, in press) that do not require parental marker genotypes but, instead, use marker genotypes of unaffected siblings. All of these approaches, however, are concerned with autosomal markers and are not directly applicable in the case of X-chromosomal markers. The lack of analogous tests for X-linked markers constitutes an important methodological gap, since there is an increasing list of (putative) disease genes on the X chromosome: examples include MAOA and MAOB, in psychiatric disease ( Karayiorgou et al. 1999; Paterson et al. 1999); the androgen-receptor gene, in prostate cancer (Taplin et al. 1995); and DYT3, in X-linked dystonia parkinsonism (Nemeth et al. 1999).
The purpose of the present article is to describe procedures that can be used to test for linkage between an X-chromosomal marker and a disease, in the presence of linkage disequilibrium between the two loci, when the sample consists of nuclear families for which there is incomplete parental marker–genotype information. As has been done by Spielman and Ewens (1998) and Knapp (1999a), we will assume that there is a specific allele (A), at a marker locus on the X chromosome, that is of particular interest. The first procedure (called “X-linked sibling TDT” [XS-TDT]) modifies the sibling TDT (S-TDT) (Spielman and Ewens 1998), whereas the second procedure follows the logic of the reconstruction-combined TDT (RC-TDT) for an autosomal marker described by Knapp (1999a). Therefore, it will be called the “reconstruction-combined transmission/disequilibrium test for X-chromosomal markers” (XRC-TDT). Like the RC-TDT, the X-linked RC-TDT (XRC-TDT) employs parental-genotype reconstruction and corrects for the biases resulting from the reconstruction. The XRC-TDT does not rely on population marker-allele frequencies; it combines data from families in which parental genotypes are available with data from families in which genotypes of unaffected sibs are available but parental marker information is incomplete. For both the XS-TDT and the XRC-TDT, it is possible to calculate exact P values in the same way as has been described for the RC-TDT by Knapp (1999b).
We will be using the following notation. The sample consists of m nuclear families (parents and offspring). For 1⩽i⩽I, nfai and nmai denote, respectively, the number of affected daughters and affected sons, nfui and nmui denote, respectively, the number of unaffected daughters and unaffected sons, and nfci=nfai+nfui and nmci=nmai+nmui denote, respectively, the total number of daughters and sons, in family i. The number of affected offspring and the number of unaffected offspring are given by nai=nfai+nmai and nui=nfui+nmui, respectively. Finally, nci=nfci+nmci=nai+nui denotes the size of the sibship in family i. In each family, the offspring has been typed at the marker locus, but the marker genotypes for one or more parents may be unavailable in some families. Let Ngai (Ngui) be random variables denoting the number of affected (unaffected) offspring with genotype g, in family i. Genotypes consisting of a single allele correspond to sons, whereas genotypes with two (not necessarily different) alleles correspond to daughters. Small letters (i.e., ngai and ngui) are used to denote the observed values of Ngai and Ngui. Furthermore, let Ngi:=Ngai+Ngui and ngi:=ngai+ngui denote, respectively, the random variable and the observed number of offspring with genotype g, in family i. Because there are, at most, three different alleles segregating in a single nuclear family, and because families without allele A are uninformative for the present purpose, it is sufficient to consider a marker locus with three alleles, A–C, in which B and C may denote different alleles, across families. Tfi:=2NAAai+NABai+NACai denotes the number of A alleles in affected daughters; that is, Tfi counts the number of transmissions of the A allele from both parents, whereas Tmi is this number in affected sons (i.e., Ti=NAai). Finally, Ti=Tfi+Tmi is the total number of A alleles in affected offspring in family i.
The autosomal RC-TDT reduces to the TDT in families in which both parental marker genotypes are available and reduces to the S-TDT when parental genotypes cannot be reconstructed. Therefore, the first step toward adaptation of the RC-TDT to X-chromosomal markers is to describe variants, of both the TDT and the S-TDT, that can be used for X-chromosomal markers.
Adapting the TDT to X-chromosomal markers (a procedure that we will denote as “XTDT”) is straightforward: the XTDT simply counts the number of transmissions and the number of nontransmissions of allele A from heterozygous mothers to their affected offspring. Under H0, a heterozygous mother transmits each of her alleles, with probability .5, to each affected child. (Incidentally, we note that, if the father’s genotype is A, then Tfi, as defined above, is not equal to the number of A transmissions from heterozygous mothers to their affected daughters, because Tfi counts the number of A transmissions from the fathers as well; however, this linear transformation is irrelevant.)
Adapting the S-TDT to X-chromosomal markers (a procedure that we will denote as “XS-TDT”) is slightly less obvious. To illustrate the problem, consider the example of a family with one affected child and one unaffected child. Furthermore, assume that, for this family, nAB=1 and nB=1. Then, there are two possibilities for this family: either (1) the affected child has genotype AB or (2) the affected child has genotype B. The hypergeometric distribution used by Spielman and Ewens (1998) for their S-TDT would assign null probabilities of .5 to each of these two alternatives; however, these null probabilities are not adequate for a disease that has differing prevalences in males and females. Such gender-specific prevalence rates seem to be the rule rather than the exception. If the disease of interest is more frequent in females than in males, alternative (1) has a higher probability than does alternative (2), even if the null hypothesis is true. This example shows that naive adaptation of the S-TDT could inflate the type 1–error rate of the resulting XS-TDT. One way around this problem is to include within the model a parameter for the ratio of the prevalence rates in the two genders; however, since misspecification of this parameter can invalidate the resulting test, we prefer another approach: the sibship of each family is divided into two strata (which we will call “subsibships”), with the first subsibship consisting of daughters and with the second subsibship consisting of sons. The S-TDT is then applied to each of the two subsibships separately; that is, first, the null distribution of Tfi is calculated conditional on nfa, nfu, and the observed marker genotype distribution in the daughters, and, second, the null distribution of Tmi is calculated conditional on nma, nmu, and the observed marker genotype distribution in the sons. If the paternal genotype is missing but the maternal genotype is known, then the male subsibship is analyzed by use of the XTDT. Splitting the sibship into subsibships is justified because, under H0, Tfi and Tmi are independent.
To adapt the RC-TDT to X-chromosomal markers, it is necessary to calculate the null distribution of the number of A alleles in affected offspring, conditional on the event that the number of A alleles can be determined in the missing parental genotypes. Roughly speaking, this means that parental genotypes can be reconstructed; but note that, for both the autosomal RC-TDT and the X-chromosomal RC-TDT, reconstruction does not require the unambiguous determination of missing parental alleles that are different from A. For X-chromosomal markers, three situations have to be distinguished: (a) both parental genotypes are missing; (b) the maternal genotype is missing but the paternal genotype has been typed; and (c) the paternal genotype is missing but the maternal genotype has been typed.
When both parental genotypes are missing, the aim of parental-genotype reconstruction is to answer the following two questions: Is the mother heterozygous for allele A? Is the father’s genotype equal to A? It is possible that, on the basis of the observed genotypes in the sibship, the first of these questions can be positively answered but the second question cannot be answered—that is, it can be determined that the mother is heterozygous but it cannot be determined whether the father is A or not A. This situation occurs if the sons have two different genotypes (say, A and B) but all daughters have the genotype AB (i.e., NAB=nfc). In this case, the parental mating type can be either AB×A or AB×B and is denoted by AB×? in table 1. Knowing that the mother is heterozygous for allele A is sufficient for counting the transmissions and nontransmissions of allele A to her affected sons. For affected daughters in this case, however, it cannot be decided whether all of them received the A allele or the B allele from their mother. Effectively, for this case, only maternal transmissions to sons provide information.
Table 1.
First and Second Moment of T in Families with Reconstructed Parental Genotypes (Both Parental Genotypes Missing) for X-Linked Markers
| Parental Mating Type | R | EH0(T∣R) | EH0(T2∣R) |
| AB×? | (NA>0) and (NB>0) and (NAB=nfc) | 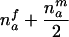 |
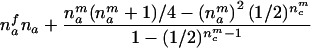 |
| AB×A | (NAA>0) and (NAB>0 or NB>0) | 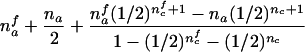 |
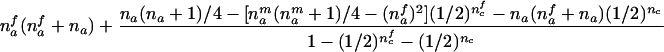 |
| AB×B | (NBB>0) and (NAB>0 or NA>0) | 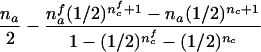 |
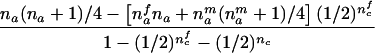 |
| AB×C: | |||
| nmc=0 | (NAC>0 and NBC>0) | 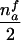 |
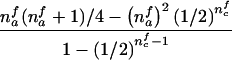 |
| nmc>0 | (NAC>0 and NBC>0) or (NBC>0 and NA>0) or (NA>0 and NB>0 and NAC>0) | 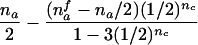 |
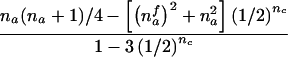 |
The third and fourth column of the first row in table 1 contain expressions for the conditional expectation of Ti and T2i, given that the missing maternal genotype can be reconstructed but that the paternal genotype cannot be reconstructed. The method used to obtain these expressions is very similar to that used by Knapp (1999a) for his table 1, but the algebra is even simpler in the case of X-chromosomal markers. From these expressions (the family index i has been dropped in table 1), it can be seen that the conditional null variance of Ti becomes
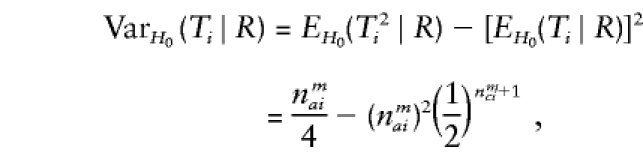 |
which does not depend on the number of affected or unaffected daughters in the family and which is always smaller than the variance in the number of A alleles transmitted to nmai affected sons by a heterozygous mother.
For the three possible parental mating types, the remaining rows in table 1 present conditions that are necessary and sufficient to allow reconstruction of both missing parental genotypes and the conditional first and second moments of Ti. The condition given in table 1 for an AB×C mating is not sufficient for an exact reconstruction (e.g., in case that NBCi>0 and NAi>0, the mating type can be either AB×C or AC×B) but is sufficient for answering the two questions listed two paragraphs above. Note that, for an AB×C mating, table 1 contains two different sets of formulas, corresponding to the situation when there are sons in the family (i.e., nmc>0) and to the situation when there are no sons in the family (i.e., nmc=0).
We now consider the case in which only the maternal genotype is missing. As can be seen from table 2, the null expectation of the number of A alleles in affected offspring in families, when the missing maternal genotype can be reconstructed, always equals the null expectation of this number for families with completely typed parents. However, in the case of na>1, the null variance (given in the fourth column in table 2) is smaller than the corresponding variance for families with typed parents; for families with a single affected child (i.e., na=1), however, these two variances are equal.
Table 2.
Expectation and Variance of T, in Families with Reconstructed Parental Genotypes (only the Maternal Genotype Missing), for X-Linked Markers
| Parental Mating Type | R | EH0(T∣R) | 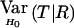 |
| AB×A | (NAA>0 or NA>0) and (NAB>0 or NB>0) | 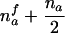 |
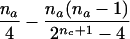 |
| AB×B | (NAB>0 or NA>0) and (NBB>0 or NB>0) | 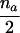 |
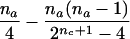 |
| AB×C | (NAC>0 or NA>0) and (NBC>0 or NB>0) | 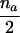 |
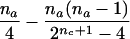 |
When the paternal genotype is missing but the maternal genotype has been typed and is known to be heterozygous for allele A, the number of transmissions of allele A by this mother to her affected sons can be counted and is binomially distributed B(nma, 1/2), under the null hypothesis. The missing paternal genotype is required only in order to count the transmissions to her affected daughters. Therefore, table 3 presents the null expectation and variance of the number Tfi of A alleles in affected daughters, conditional on the event that the missing paternal genotype can be reconstructed. For mating type AB×C, the paternal genotype can be reconstructed if there is at least one daughter; if there is no daughter, the paternal genotype is of no interest. Therefore, the condition for mating type AB×C is empty.
Table 3.
Expectation and Variance of Tf, in Families with Reconstructed Parental Genotypes (only the Paternal Genotype Missing), for X-Linked Markers
| Parental Mating Type | R | EH0(Tf∣R) | 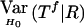 |
| AB×A | (NAA>0) | 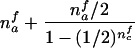 |
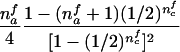 |
| AB×B | (NBB>0) | 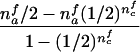 |
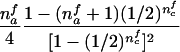 |
| AB×C | … | 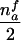 |
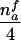 |
Now we are ready to describe the XRC-TDT statistic. As does the RC-TDT, the XRC-TDT can combine families with typed parental genotypes and families with reconstructed parental genotypes. The (autosomal) RC-TDT distinguishes several categories of families. One of these categories corresponds to families in which at least one parental genotype is missing and cannot be reconstructed but in which the condition for the S-TDT is satisfied. For this category, the RC-TDT reduces to the S-TDT. This kind of family, however, does not exist in the context of the analysis of an X-chromosomal marker. In the case that at least one parental genotype is missing and the genotypes of the offspring do not satisfy the conditions given in tables 1–3, the family also cannot be used by the XS-TDT. The reason is that a subsibship is only suitable for the XS-TDT if two different genotypes are being observed; however, the presence of two different genotypes in the daughters always enables the reconstruction of both parents' genotypes, and observing two different genotypes in the sons enables the reconstruction of the maternal genotype (table 1, first row). Thus, the test statistic of the XRC-TDT is given by
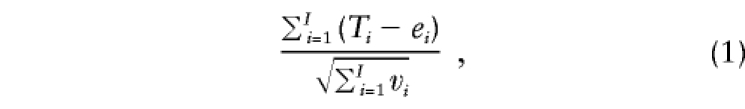 |
where the summation is over all families in the sample in which either (i) both parents are typed and the mother is heterozygous for allele A or (ii) the family belongs to one of the cases described in tables 1–3. The terms ei and vi in test statistic (1) denote the appropriate null expectation and variance—that is, ei=nai/2 and vi=nai/4, in the case of situation (i), and ei and vi, as given by tables 1–3, in the case of situation (ii). The distribution of test statistic (1) is approximately the standard normal distribution under the null hypothesis of no linkage. Alternatively, exact P values can be assigned to this test statistic in the same way as has been described, by Knapp (1999b), for the S-TDT and the RC-TDT.
We conducted a simulation study to compare the power of the XRC-TDT versus the power of the XS-TDT, which splits sibships into subsibships. These simulations closely followed the approach used by Boehnke and Langefeld (1998) and Knapp (1999a). In brief, the disease locus possessed two alleles, D and d, with frequencies p and q,respectively, with penetrances in females 1⩾fDD⩾fDd⩾fdd⩾0 and penetrances in males 1⩾gD⩾gd, not all equal. For the predisposing genotype, the penetrance fDD in females was fDD=.2, .5, or .8. Dominant (fDD=fDd), additive (fDd=(fDD+fdd)/2), and recessive (fDd=fdd) models were simulated; for each model, a disease prevalence (KP) of 5% in both sexes, an attributable fraction of 50%, and fdd=gd were assumed. Then, the disease allele frequency p and the penetrance gD was able to be calculated. The marker consisted of six codominant alleles with population frequencies .4, .2, .1, .1, .1, and .1 and was completely linked to the disease locus. Again, in the manner of Boehnke and Langefeld (1998), the haplotype frequencies were set to yield, for the first marker allele, a frequency difference of C=.15 between randomly selected affected and unaffected individuals. In addition, it was assumed that all remaining marker-allele frequencies are proportionately reduced in affected individuals. Under these conditions, the population frequency (hkD) of the haplotype with marker allele k and disease allele D then was found to be
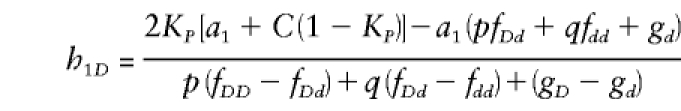 |
and
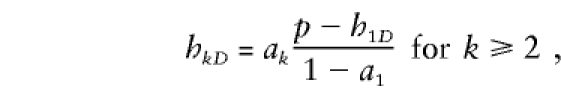 |
where ak denotes the population frequency of marker allele k.
Each simulated sample consisted of families with an identical number, nc, of sibs in each family (with nc=2, 4, or 6), which were ascertained on the basis of the presence of an affected child. The gender of the proband and of his or her siblings was randomly assigned, with probability .5. The number of families per sample was 1,200/nc; that is, each sample consisted of 1,200 children. R=500 replicate samples were generated, under 27 different simulation conditions (i.e., for each combination of mode of inheritance, fDD, and nc). For each replicate sample, exact P values for XS-TDT and XRC-TDT were calculated. For the XRC-TDT, it was assumed that either no parental marker information or only maternal marker information or only paternal marker information was available.
The results of the simulations are presented in table 4, which contains power estimates, at significance level α=.001, for nine disease models. These disease models are denoted as “D,” “A,” and “R”—for the mode of inheritance in females (i.e., dominant, additive, and recessive)—and as “1,” “2,” and “3”—for the value of fDD (i.e., .2, .5., and .8). The XS-TDT does not distinguish between families in which both parental genotypes are missing and families in which only the maternal genotype is missing. No results are given for the XRC-TDT when nc=2 and both parental genotypes are missing in all families. In this case, XRC-TDT and XS-TDT are identical, as can be seen from the formulas given in table 1. For the purpose of comparison with the situation in which parental genotype information is complete, the second column of table 4 gives power estimates for the XTDT for samples of 600 families with a single affected child each.
Table 4.
Simulated Power of the XS-TDT and XRC-TDT, for Sibships with at Least One Affected Sib (α=.001)
|
Simulated Power forb |
|||||||||||||||
| 600 Families with Two Siblings Each |
300 Families with Four Siblings Each |
200 Families with Six Siblings Each |
|||||||||||||
| XS-TDT |
XRC-TDT |
XS-TDT |
XRC-TDT |
XS-TDT |
XRC-TDT |
||||||||||
| Model | XTDTa | Both/Maternal | Paternal | Maternal | Paternal | Both/Maternal | Paternal | Both | Maternal | Paternal | Both/Maternal | Paternal | Both | Maternal | Paternal |
| D1 | .93 | .18 | .96 | .55 | .97 | .44 | .83 | .75 | .70 | .85 | .53 | .73 | .72 | .68 | .76 |
| D2 | .94 | .17 | .99 | .58 | 1.0 | .77 | .97 | .94 | .92 | .98 | .92 | .97 | .97 | .95 | .98 |
| D3 | .93 | .19 | 1.0 | .60 | 1.0 | .86 | .99 | .96 | .97 | .98 | .96 | .98 | .97 | .97 | .98 |
| A1 | .92 | .19 | .92 | .54 | .96 | .33 | .70 | .63 | .55 | .77 | .35 | .56 | .54 | .50 | .58 |
| A2 | .93 | .17 | .97 | .56 | .98 | .54 | .87 | .81 | .77 | .89 | .63 | .82 | .79 | .77 | .85 |
| A3 | .94 | .17 | .99 | .55 | .99 | .72 | .96 | .91 | .87 | .97 | .84 | .94 | .93 | .91 | .95 |
| R1 | .94 | .20 | .72 | .37 | .82 | .30 | .49 | .46 | .39 | .57 | .27 | .37 | .41 | .33 | .45 |
| R2 | .92 | .18 | .74 | .38 | .86 | .38 | .60 | .64 | .59 | .74 | .43 | .52 | .57 | .55 | .59 |
| R3 | .93 | .20 | .74 | .38 | .90 | .47 | .66 | .71 | .68 | .82 | .54 | .62 | .71 | .70 | .75 |
For 600 families with a single affected child each.
Both = both parental genotypes are missing in all families; Maternal = only the maternal genotype is missing in all families; Paternal = only the paternal genotype is missing in all families.
With regard to the situations presented in the table, we make the following four observations. First, the XRC-TDT is usually much more powerful than the XS-TDT. The main reason for this phenomenon is that the XS-TDT partitions the sibships into subsibships, whereas the XRC-TDT can avoid such partitioning. Second, for both XRC-TDT and XS-TDT, families with missing paternal marker data contain much more information than is derived from families with missing maternal marker data. Third, the XS-TDT does not distinguish between families with missing maternal genotypes and families with both parental genotypes missing. (That can be quite different for the XRC-TDT: for sib pairs, families with missing maternal genotype contain much more info than is contained by families with both parents missing; but, for sibships consisting of four or more children, the situation in which maternal genotypes are missing is generally as bad as [or worse than] the situation in which the genotypes of both parents are missing.) Fourth, for the XRC-TDT, 300 sibships consisting of four children each are approximately as good as (and sometimes better than) 200 sibships consisting of six children each. For the XS-TDT, the situation is more complicated and depends on which parent is missing. (An SAS macro (SAS Institute, Inc. 1990) that calculates the XS-TDT and XRC-TDT test statistics, as well as their respective exact P values, can be obtained, via e-mail, from the corresponding author for this report.)
Acknowledgments
We thank Joan Bailey-Wilson for bringing this problem to our attention and for many helpful discussions. S.H. is supported by a scholarship from the BONFOR Research Commission of the Medical University at the University of Bonn (Bonn, Germany).
References
- Boehnke M, Langefeld CD (1998) Genetic association mapping based on discordant sib pairs: the discordant-alleles test. Am J Hum Genet 62:950–961 [DOI] [PMC free article] [PubMed]
- Curtis D (1997) Use of siblings as controls in case-control association studies. Ann Hum Genet 61:319–333 [DOI] [PubMed]
- Horvath S, Laird NM (1998) A discordant-sibship test for disequilibrium and linkage: no need for parental data. Am J Hum Genet 63:1886–1897 [DOI] [PMC free article] [PubMed]
- Karayiorgou M, Sobin C, Blundell S, Blundell ML, Brandi LG, Malinova L, Goldberg P, et al (1999) Family-based association studies support a sexually dimorphic effect of COMT and MAOA on genetic susceptibility to obsessive-compulsive disorder. Biol Psychiatry 45:1178–1189 [DOI] [PubMed]
- Knapp M (1999a) The transmission/disequilibrium test and parental-genotype reconstruction: the reconstruction-combined transmission/disequilibrium test. Am J Hum Genet 64:861–870 [DOI] [PMC free article] [PubMed]
- Knapp M (1999b) Using exact P values to compare the power between RC-TDT and S-TDT. Am J Hum Genet 65:1208–1210 [DOI] [PMC free article] [PubMed]
- Nemeth AH, Nolte D, Dunne D, Niemann S, Kostrzewa M, Peters U, Fraser E, et al (1999) Refined linkage disequilibrium and physical mapping of the gene locus for X-linked dystonia-parkinsonism (DYT3). Genomics 60:320–329 [DOI] [PubMed]
- Paterson AD (1999) Sixth World Congress of Psychiatric Genetics: X-Chromosome Workshop. Am J Med Genet 88:279–286 [PubMed]
- Rabinowitz D, Laird NM. Adjusting association tests for population admixture with arbitrary pedigree structure and arbitrary missing marker information. Hum Hered (in press) [DOI] [PubMed] [Google Scholar]
- SAS Institute, Inc (1990) SAS language: reference, version 6, 1st ed. SAS Institute, Cary, NC [Google Scholar]
- Schaid DJ, Rowland C (1998) Use of parents, sibs, and unrelated controls for detection of associations between genetic markers and disease. Am J Hum Genet 63:1492–1506 [DOI] [PMC free article] [PubMed]
- Spielman RS, Ewens WJ (1998) A sibship test for linkage in the presence of association: the sib transmission/disequilibrium test. Am J Hum Genet 62:450–458 [DOI] [PMC free article] [PubMed]
- Spielman RS, McGinnis RE, Ewens WJ (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed]
- Taplin ME, Bubley GJ, Shuster TD, Frantz ME, Spooner AE, Ogata GK, Keer HN, et al (1995) Mutation of the androgen-receptor gene in metastatic androgen-independent prostate cancer. N Engl J Med 332:1393–1398 [DOI] [PubMed]


