Detection of Disease Genes by Use of Family Data. II. Application to Nuclear Families

Abstract

Two likelihood-based score statistics are used to detect association between a disease and a single diallelic polymorphism, on the basis of data from arbitrary types of nuclear families. The first statistic, the nonfounder statistic, extends the transmission/disequilibrium test to accommodate affected and unaffected offspring and missing parental genotypes. The second statistic, the founder statistic, compares observed or inferred parental genotypes with those of some reference population. In this comparison, the genotypes of affected parents or of those with many affected offspring are weighted more heavily than are the genotypes of unaffected parents or of those with few affected offspring. Genotypes of single unrelated cases and controls can be included in this analysis. We illustrate the two statistics by applying them to data on a polymorphism of the SDR5A2 gene in nuclear families with multiple cases of prostate cancer. We also use simulations to compare the power of the nonfounder statistic with that of the score statistic, on the basis of the conditional logistic regression of offspring genotypes.

Introduction

We have previously considered the use of two likelihood-based score statistics in the evaluation of chromosomal regions for the presence of a locus that alters risk for a disease (Whittemore and Tu 2000). The first statistic, the nonfounder statistic (NFS), is conditioned on the observed or inferred distribution of parental genotypes. This statistic evaluates disequilibrium in the transmission of alleles from parents to affected and unaffected offspring, and it does not use data on parental phenotypes. When all parental genotypes are known and when genotypes of unaffected offspring are ignored, the NFS reduces to one of Schaid's (1996) proposed score statistics, which include the transmission/disequilibrium-test (TDT) statistic (Ott 1989; Terwilliger and Ott 1992; Knapp et al 1993; Spielman et al 1993; Ewens and Spielman 1995; Spielman and Ewens 1996). If not all parental genotypes are known, then use of the TDT can lead to bias (Curtis and Sham 1995). Use of the NFS avoids this problem, since, for each pair of parents, a probability distribution for the parental genotypes is assigned, conditional on the genotype data observed for the entire family.

The second statistic, the founder statistic (FS), compares the observed or inferred parental genotypes with those in some reference population. In contrast to their role in the NFS, parental phenotypes, when known, play an important role in the FS. Moreover, a parent’s contribution to the FS depends not only on his or her phenotype (if known) but, also, on the phenotypes of his or her offspring. Parents with many affected and few unaffected offspring contribute more to the statistic than do parents with few affected offspring.

In the present study, we examine these two statistics when they are applied to nuclear families, with the objective of evaluating the association between disease and a single polymorphism. Although the statistics apply to multiallelic markers, for notational simplicity, we shall assume that the polymorphism consists of two alleles—labeled B₁ and B₂—one of which may confer an increased disease risk. We also assume that interest centers on the etiologic relevance of this polymorphism and not on that of some nearby unmeasured locus. The families may vary in size, and they may also vary with respect to the available information on the genotypes and phenotypes of the family members, with some families having only partial information available. We illustrate the statistics by applying them to data on prostate cancer in nuclear families, in relation to a polymorphism of the gene encoding the enzyme type II 5α-reductase. Finally, we relate the NFS to the statistic discussed both by Spielman and Ewens (1998) and Schaid and Rowland (1998) and known as the “sib transmission disequilibrium test (STDT) statistic”; we then use simulations to compare the powers of the two statistics.

Score Statistics

Family Genotypes

We wish to use the available data on the genotypes and phenotypes of members of N unrelated nuclear families, to test the null hypothesis that the polymorphism with alleles B₁ and B₂ is unrelated to disease risk. We assume that the genotypes of the offspring are known but that the parental-genotype information may be incomplete. In addition, the phenotypes of some family members may be unknown. We shall assign a numerical count to each of the three possible genotypes for an individual. Let c_g denote the count assigned to genotype g, where g=0, 1, or 2 denotes the number of B₁ alleles in the genotype. As discussed in the companion article that appears in this issue of the Journal (Whittemore and Tu 2000), all of the statistics are invariant under linear transformations of the three genotype counts. Therefore, we arbitrarily assign c₀=0 and c₂=1, so that the genotypes B₂B₂ and B₁B₁ receive counts of 0 and 1, respectively. Our assignment for the count c₁ then reflects the weight we give to heterozygotes, relative to weights of 0 and 1 for the two homozygotes. For example, the count c₁=1/2 gives heterozygotes a weight that is intermediate between the two, and the count c₁=1 gives heterozygotes the weight of the B₁B₁ genotype, whereas the count c₁=0 gives them the weight of the B₂B₂ genotype.

Let x_νrs denote the probability that, in the νth family ν=1,...,N, the mother has genotype r and the father has genotype s, given the genotype information available for the entire family r, s=0,1,2. For example, if the parents are untyped but two of their offspring have genotypes B₁B₁ (g=2) and B₂B₂ (g=0), then x_ν11=1. We denote the corresponding marginal probabilities that the mother has genotype r and that the father has genotype s as 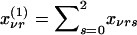and 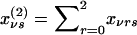, respectively. Appendix A shows the joint probabilities x_νrs, which depend on the prior probabilities η_s that a parent has genotype s, s=0,1,2. Under the null hypothesis of no association with the disease, these probabilities are those of the reference population, which we denote as u₀,u₁,u₂. However, if the polymorphism is associated with the disease and if the families have been selected to contain multiple cases of the disease, then the probabilities are η₀,η₁,η₂ and the two sets of probabilities differ. We shall use the method of maximum likelihood to estimate η₀,η₁,η₂, as described in Appendix A.

Family Phenotypes

We label the n_ν members of the νth family as 1,2,...,n_ν, ν=1,...,N. Indices 1 and 2 denote the mother and father, respectively, and indices 3,...,n_ν denote the offspring. Following the discussion of the companion article (Whittemore and Tu 2000), we assign to individual i the phenotypic value

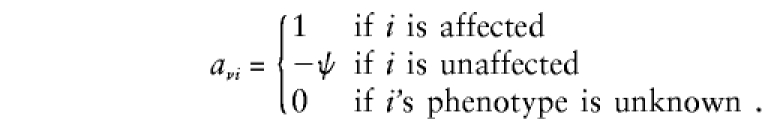Here ψ is a specified number that determines the relative contributions of affected and unaffected individuals to the test statistics. For example, ψ might be chosen as the odds of disease in the general population. Thus, for rare diseases, ψ≪1, so that, in comparison with affected individuals, the unaffected individuals contribute little. In contrast, choosing ψ=1 places equal weights on affected and unaffected individuals, whereas choosing ψ=0 ignores unaffected individuals.

NFS

The NFS of equation (17) in the companion article (Whittemore and Tu 2000) is as follows:

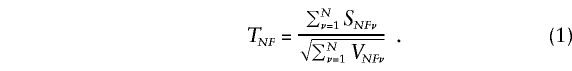For this NFS, the summand S_NFν for the νth family, ν=1,...,N, is given by equation (11) of the companion article (Whittemore and Tu 2000). In Appendix B, we show that

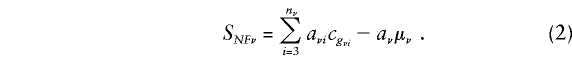In this expression, 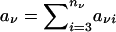is the sum of the offspring-phenotype scores, and μ_ν denotes the null expectation of the count of any one offspring, given the available information on the parental genotypes. Also in equation (1), V_NFν represents the null variance of S_NFν, conditional on the available genotype information for the parents of the νth family. From equation (2), we see that, under the assumption of independence of parental genotypes (i.e., no assortative mating),

Here 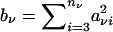, σ²_ν represents the null variance of the genotype count of one offspring, and ξ_ν is the null covariance of the genotype counts of two offspring, for offspring in the νth family.

The null mean μ_ν, null variance σ²_ν, and null covariance ξ_ν of the offspring-genotype scores are as follows:

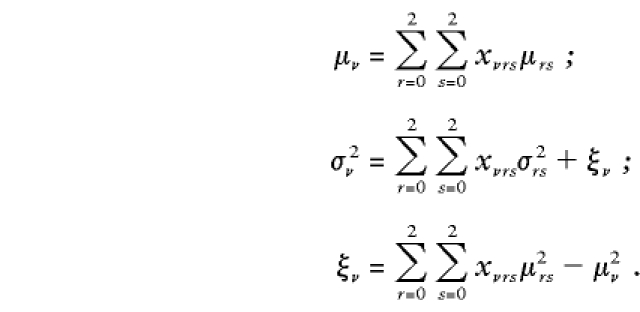Here μ_rs=μ_sr and σ²_rs=σ²_sr denote the mean and variance for an offspring whose parents have genotypes r and s, as shown in the Mean and Variance columns of table 1. When parental genotypes are known, the covariance of offspring genotypes is 0, since parental meioses for any two offspring are independent. Notice that, in the Variance column of table 1, σ²_rs=0 when both parents are homozygous. This implies that, for these parental genotypes, the observed offspring genotype always equals its mean value. From equations (2) and (3), we see that S_NFν=V_NF=0 for families in which both parents known to be homozygous and that, therefore, these families do not contribute to the test statistic.

Table 1.

Mean and Variance of Genotype Count for One Offspring^a and Distribution of Genotypes for n Offspring, Given the Parental Mating Type

Parental Mating Type (r×s)	Mean (μrs)	Variance (σ2rs)	Genotype Probability for n Offspringb (φrs[n11,n12,n22])
B1B1×B1B1 (2×2)	1	0	1if n12=n22=00otherwise
B1B1×B1B2 (2×1)	1/2(1+c1)	1/4(1-c1)2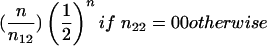
B1B1×B2B2 (2×0)	c1	0	1if n11=n22=00otherwise
B1B2×B1B2 (1×1)	1/4+ 1/2c1	1/16(4c21-4c1+3)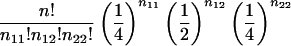
B1B2×B2B2 (1×0)	1/2c1	1/4c21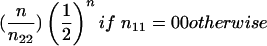
B2B2×B2B2 (0×0)	0	0	1if n11=n12=00otherwise

^aWith c₀=0 and c₂=1.

^bn_ij is the number of offspring with genotype B_iB_j, i, j=1,2, with n₁₁+n₁₂+n₂₂=n.

Under the null hypothesis, T_NF has, asymptotically, a Gaussian distribution with a mean of 0 and a variance of 1. In the special case that parental genotypes are known, ψ=0, and c₁=1/2, T_NF is the statistic for the TDT (Spielman and Ewens 1996). When ψ=0 and c₁=0 or 1, T_NF is the statistic proposed both by Schaid (1996) and Schaid and Li (1997).

FS

The FS described in equation (17) of the companion article (Whittemore and Tu 2000) is as follows:

The summand S_Fν is given by equation (13) in the companion article (Whittemore and Tu 2000). In Appendix B, we show that

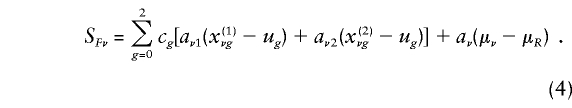In this instance, 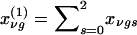and 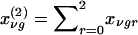are the probabilities that the mother and father, respectively, have genotype g, given the genotypes observed for the family. Also, 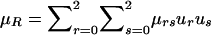is the expected count for an offspring of a random pair of parents in the reference population. Note that each family member with a known phenotype contributes a term to the founder score. Parents contribute the difference between their observed or inferred genotype count and the observed or inferred genotype count of a random individual in the reference population. Offspring, in contrast, contribute the difference between their expected count, given the observed or inferred genotypes of their parents, and the expected count, given that their parents were randomly selected from the reference population. When c₁=1/2, S_Fν reduces to

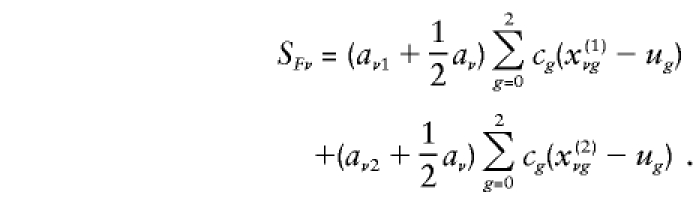In this instance, S_Fν is the difference between the observed or inferred parental counts and their null expectation, summed over the two parents. Moreover, the difference between each parent’s count and its null expectation is weighted by his or her phenotype value plus half the sum of the phenotype values for his or her offspring. The null variance of S_Fν is V_Fν=E[S²_Fν], which we shall estimate with the use of 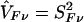. Under the null hypothesis, T_F has, asymptotically, a Gaussian distribution with a mean of 0 and a variance of 1, provided that the reference-genotype probabilities u₀, u₁, u₂ correctly represent those of the parental population.

Total Score Statistic

Unlike the NFS, the FS is vulnerable to bias resulting from misspecification of the parental-genotype distribution, particularly that of the reference-genotype probabilities u₀, u₁, and u₂. Separate evaluation and comparison of the two test statistics may help to quantify how much of an apparent association between parental and reference genotypes is the result of association in the absence of linkage disequilibrium. Presence of a significantly positive or negative FS, in the absence of an NFS with the same sign, suggests that the FS may be biased as a result of misspecification of the parental-genotype distribution. When both statistics have the same sign, it may be desirable to combine them to form the total score statistic

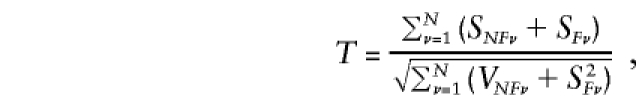where S_NFν, S_Fν, and V_NFν are given by formulas (2), ( 4), and (3), respectively. T has an asymptotic Gaussian distribution with a mean of 0 and variance of 1 under the null hypothesis, provided that the reference-genotype probabilities correctly represent those of the parental population.

Application to Prostate Cancer

We illustrate the test statistics by applying them to genotypes in 126 nuclear families ascertained because of multiple cases of prostate cancer. The genotypes give the number of T (versus A) alleles at a diallelic polymorphism of the steroid 5α-reductase (SRD5A2) gene. This example is taken from an unpublished study (C.-L. Hsieh, I. Oakley-Girvan, R. R. Balise, R. Gallagher, L. N. Kolonel, A. Wu, and A. S. Whittemore, unpublished data). The A/T polymorphism is the result of a missense mutation, known as “A49T,” that replaces alanine (A) at codon 49 with threonine (T). It has been suggested that this mutation increases the risk of prostate cancer by increasing steroid 5α-reductase activity, thereby increasing the rate at which testosterone is converted to its active metabolite dihydrotestosterone (Makridakis et al. 1998; Reichardt et al. 1998).

Table 2 shows the distribution of family structures and phenotypes for the 126 families. Because prostate cancer is a disease of late onset (median age at diagnosis 72 years), only seven fathers and four mothers were available for genotyping. Females with known genotypes were included in the analysis and were assigned a phenotype value a_ν=0. These females contribute information about the parental-genotype distribution. The T allele was found in 11/126 families. This subset of families included 27 typed affected sons, who had frequencies of 6, 10, and 11 for genotypes TT, AT, and AA, respectively, and 7 typed unaffected sons, who had corresponding frequencies of 0, 3, and 4. There were no typed fathers in the 11 families segregating the T allele. We assumed random mating of parents, with respect to the genotypes of the A/T polymorphism, and, for the founder statistic, we assumed the values u₂=.02, u₁=.04, and u₀=.94 for the reference-genotype frequencies. These values were obtained from a sample of 191 white males without prostate cancer (J. Reichardt, personal communication). We treated these genotype frequencies as known constants.

Table 2.

Distribution of 126 Nuclear Families with Multiple Cases of Prostate Cancer, According to Family Structure and Phenotype

	No. of Instances of Father’s Phenotype
No. of Sons Affected/Unaffected	Affected	Unaffected	Unknown	Total
1/1	10	7	0	17
1/2	2	7	0	9
2/0	11	23	3	37
2/1	9	12	0	21
2/2	3	4	1	8
2/3	1	0	0	1
2/4	1	0	0	1
3/0	3	14	2	19
3/1	3	2	0	5
3/2	0	2	0	2
3/3	0	1	0	1
4/0	0	4	0	4
4/1	0	0	1	1
Total	43	76	7	126

Table 3 summarizes the values of the FS, NFS, and total test statistic, for the c₁=1, 1/2, and 0 weight specifications for heterozygotes and for the ψ=1 and π/(1+π) weight specifications for unaffected individuals. We took π to be the prevalence of prostate cancer in the population, which we assumed was 10%. As shown in table 3, the NFS T_NF is significantly elevated (p<.01, one-tailed test) when c₁=0, regardless of how the unaffected individuals are weighted. The c₁=0 weight assignment for heterozygotes compares prevalences of the TT genotype in affected and unaffected sons. Thus, the statistical significance of these NFSs reflects the higher prevalence of TT homozygotes among affected sons, compared with unaffected sons.

Table 3.

NFS, FS, and Total Score Statistics for Association between Prostate Cancer and the T Allele of the A49T Polymorphism of the SRD5A2 Gene in 126 Nuclear Families

	TNF (p)
Weight c1 andWeight Ψ	NFSa	FS	Total
1:
1	.02 (.45)	.50 (.31)	.30 (.38)
.11	−.94 (.83)	.71 (.66)	.02 (.68)
1/2:
1	.90 (.18)	1.10 (.14)	1.39 (.08)
.11	−.00 (.50)	.87 (.19)	.72 (.24)
0:
1	2.50 (<.01)	2.10 (.02)	3.27 (<.01)
.11	2.40 (<.01)	1.28 (.10)	2.63 (<.01)

^aOne-tailed p value, by means of Gaussian approximation.

The FS T_F also is positive when c₁=0, but it achieves statistical significance only when ψ=1. For both values of ψ, however, the total score statistic is significant (p<.01). The FS did not vary appreciably, with respect to choice of the reference-genotype frequencies u₀,u₁,u₂. For example, when we used u₀,u₁,u₂=.01, .03, .96, the FS for c₁=0 changed from 2.19 to 1.96 and from 1.17 to 1.64 for ψ=1 and ψ=.11, respectively. In summary, evaluation of both the FSs and NFSs suggests an association between prostate-cancer risk and homozygosity for the TT allele.

Comparison with Other Statistics

We consider the analysis of genotypes in sibships when all parental genotypes are missing, either by design or as a result of the disease having a late onset. Several authors have proposed ways to use the genotype information of offspring when parental genotypes are partially or completely missing. Curtis (1997) and Knapp (1999) have suggested (a) inclusion, in the analysis, of the types of sibships for which parental genotypes can be reconstructed from genotypes of the offspring and (b) avoidance of bias in the test statistic (Curtis and Sham 1995) by means of conditioning its null distribution on the types of sibships included. However, this approach ignores the information from sibships for which parental genotypes are only partially reconstructable. Martin et al. (1998) have proposed the same type of parental-genotype reconstruction considered in the present study, with the additional assumption that the marker alleles are in Hardy-Weinberg equilibrium. Spielman and Ewens (1998), Schaid and Rowland (1998), and Horvath and Laird (1998) have proposed variants of the score statistics obtained from conditional logistic regression of genotypes of affected and unaffected sibs. These statistics are conditioned on the observed genotypes of the sibs in each family. Such conditioning has several advantages: it avoids the need for parental genotypes; it allows for the inclusion of other covariates, such as exogenous exposures and other genes; and it can be implemented by use of standard software. However, it also has disadvantages: it requires the presence of both affected and unaffected sibs in each sibship, thereby losing all information from, for example, affected sib pairs or trios, and it does not apply to extended families.

In the present study, we compare the theoretical basis and power of the NFS test to those of the test described as an “STDT” by Spielman and Ewens (1998) and Schaid and Rowland (1998). The STDT is based on a standardized difference between genotype counts of affected sibs and counts expected under the null hypothesis of no transmission disequilibrium, conditional on the genotypes observed in the entire sibship. Because of this conditioning, the STDT uses only those sibships with at least one affected sib and at least one unaffected sib. The NFS, in contrast, conditions only on the parental-genotype information provided by the sibs’ genotypes. This weaker conditioning implies that the NFS includes data from sibships with a common phenotype (e.g., affected sib pairs).

A second implication of the different types of conditioning that characterize the two statistics concerns their treatment of information from genotype-concordant sibships. Specifically, the NFS includes a term for such sibships, whereas the STDT does not. Consider, for example, a sibship with one affected sib and k>0 unaffected sibs, all with the genotype B₁B₁. Given the event that all sibs have this genotype, the affected sib has the genotype B₁B₁ with a probability of 1 (as observed); therefore, this sibship does not contribute to the STDT. In contrast, for the NFS, the sibs’ expected genotype counts are obtained by conditioning only on the fact that the parental genotypes could have been either B₁B₁ and B₁B₁, B₁B₁ and B₁B₂, or B₁B₂ and B₁B₂. The contribution to the NFS from this sibship is (1-kψ)(1-μ), where μ is the expected count for an offspring, given that his or her parents have one of these three mating types. Thus, unless ψ=1/k, this sibship makes a contribution to the NFS.

Since the NFS uses information on the geneological relationship of the sibs and since the STDT does not do so, one can expect the NFS to have greater power than the STDT, provided that the parental-genotype distribution is modeled correctly in the NFS. In principle, the modeling assumptions (e.g., random mating and a common distribution for all parents) could be examined by use of likelihood-ratio statistics and, if necessary, could be relaxed by use of a richer model. There is a need to evaluate the trade-off in power, robustness, and bias associated with various model assumptions.

We conducted a small simulation study to compare the power of the NFS and STDT when applied to 100 sib pairs without typed parents. We assumed various values both for the parameters in the models used to generate the sibs’ genotype data and for the parameters used to analyze the data. For some of the simulations, we assumed that all 100 sib pairs had discordant phenotypes, and, for others, we assumed that 80 sib pairs had discordant phenotypes and that 20 sib pairs were affected. A detailed description of the simulations appears in Appendix C.

Simulations under various null models (data not shown) indicated that the type I–error rates for both test statistics closely agree with the nominal rates determined by means of the Gaussian approximation. Table 4 shows power comparisons, under various alternative models, for the two tests. Several outcomes are noteworthy. The first outcome concerns the power of the NFS with the unaffected weight ψ equated to the disease odds in the population (as prescribed by the likelihood theory discussed in the companion article [Whittemore and Tu 2000]), compared with that of the NFS with equal weights for affected and unaffected sibs (ψ=1). The population-odds NFS is slightly more powerful than the equal-weights NFS, when the penetrance of the deleterious allele is low. (In table 4, the penetrance is specified by the parameter β, which represents the increase in disease risk among B₁B₁ homozygotes compared with that of B₂B₂ homozygotes.) This finding agrees with the asymptotic local optimality properties of the score statistic (Cox and Hinkley 1974). However, for a deleterious allele with high penetrance, as measured by β, the equal-weights NFS does better than the population-odds NFS. In any case, the differences in power are small.

Table 4.

Power (%) of NF and STDT Tests of Size α=.001 to Detect Association between Disease and a Diallelic Polymorphism, with the Use of Genotypes for 100 Sib Pairs

				Power for (%)
	True Modela			100 Discordant Sib Pairs			80 Discordant Sib Pairs and 20 Affected Sib Pairs
Frequency of B1	β	c1	Test Statistic	c1=1	c1=1/2	c1=0	c1=1	c1=1/2	c1=0
.2	.25	1	NF, Ψ=1	81	63	1	78	60	20
			NF, Ψ=K/(1-K)b	87	69	1	84	60	17
			STDT	81	68	0	61	40	0
.2	.5	1/2	NF, Ψ=1	84	90	22	81	85	20
			NF, Ψ=K/(1-K)	90	92	22	82	83	17
			STDT	82	87	5	61	71	0
.4	.3	0	NF, Ψ=1	2	70	93	1	70	91
			NF, Ψ=K/(1-K)	1	75	95	1	71	93
			STDT	0	53	81	0	29	62
.1	.3	1	NF, Ψ=1	72	66	1	81	71	1
			NF, Ψ=K/(1-K)	77	69	2	83	67	1
			STDT	72	65	0	69	60	0
.1	.3	1/2	NF, Ψ=1	83	86	9	86	88	13
			NF, Ψ=K/(1-K)	84	83	9	86	86	11
			STDT	81	81	0	68	70	0
.3	.3	0	NF, Ψ=1	1	39	79	0	47	85
			NF, Ψ=K/(1-K)	1	45	83	1	49	84
			STDT	1	20	58	0	15	44
.05	.35	1	NF, Ψ=1	72	67	0	78	68	1
			NF, Ψ=K/(1-K)	66	61	1	71	60	2
			STDT	63	61	0	38	32	0
.05	.8	1/2	NF, Ψ=1	86	88	5	77	78	7
			NF, Ψ=K/(1-K)	80	79	7	69	68	5
			STDT	77	76	0	44	50	0
.2	.4	0	NF, Ψ=1	0	26	61	0	34	81
			NF, Ψ=K/(1-K)	0	18	67	0	34	83
			STDT	0	4	24	0	11	31

^aP(y=1∣g=i)=0.1+c_iβ, where y is an indicator for disease, g = number of B₁ alleles in genotype, and c₀=0, c₁=1.

^bK is the population prevalence of the disease.

The second noteworthy outcome concerns the impact of misspecification of the mode of inheritance, as determined by c₁, on the power of both test statistics. Choosing the weight c₁=1/2 results in considerably more robustness than does choosing either the dominant weight c₁=1 or the recessive weight c₁=0. The weight c₁=0 performs acceptably only when the true model is recessive, and c₁=1 performs reasonably well for additive and dominant models but performs badly for a recessive model.

The third noteworthy outcome concerns the relative power of the NFS and the STDT for discordant sib pairs. In virtually all cases, the NFS outperforms the STDT, although the gain in power is usually small. Both tests do well when the data are generated according to a dominant or an additive model, provided that they are also analyzed with the use of one of these two models. If a recessive model is incorrectly applied to data generated according to a dominant or additive model, then both tests do very poorly. By contrast, when the data are generated by a recessive model (c₁=0), the NFS does considerably better than the STDT, provided that neither assumes a dominant model. Finally, as expected, the NFS does considerably better than the STDT when it is applied to a mixture of discordant sib pairs and affected sib pairs. The STDT pays a high price in power loss for exclusion of the affected sib pairs.

In conclusion, use of the NFS is preferable to use of the STDT for analysis of data that include some sibships with only affected individuals or for instances in which a recessive model cannot be excluded. In addition, if parental phenotypes are known and if one has reliable data from a reference population for comparison of parental-genotype distributions, even more power can be gained by computation of the FS and the total score statistic. The STDT performs relatively well when it is applied to discordant sib pairs without parental genotypes, provided that one is reasonably confident that a recessive model is inappropriate. Its advantages include its ease of application with the use of standard software and its freedom from model assumptions. We plan to evaluate the relative performances of the STDT, the NFS, and the reconstructed parental-genotype statistic of Knapp (1999), for sibships of various sizes and phenotypes.

Discussion

We have applied the two score statistics proposed in the companion article (Whittemore and Tu 2000), to evaluate the relationship between a binary disease and a single diallelic polymorphism, by use of data from nuclear families. This application illustrates several features of the statistics. The NFS extends the TDT and the score statistics of Schaid and Sommer (1994) and Schaid (1996), to allow for unaffected offspring and missing parental genotypes. Missing parental genotypes are replaced by a probability distribution that is conditional on the genotypes observed in the family. The parameters in this distribution are estimated by means of maximum likelihood. This approach provides a set of likelihood-ratio statistics for the testing of various assumptions about parental-genotype frequencies, including random parental mating or Hardy-Weinberg proportions, (i.e., η₂=p²₁, η₁=2p₁p₂, and η₀=p²₂, where p_i is the frequency of allele B_i in the parental population).

The FS reflects the deviation between observed (or inferred) and expected genotype counts in the parental population. At one extreme, if phenotypes have been specified only for parents, then the total score statistic reduces to that for case series and case-control comparisons (Whittemore and Tu 2000). In effect, the parents are the subjects in a case-control study. Since spouses typically share the same ethnic background, this feature could be exploited to avoid bias resulting from population stratification. At the other extreme, if phenotypes have been specified only for offspring, then the FS reflects additional information that is available in the genotypes of parents of offspring with the given phenotypes. If independent data can be used to estimate the marker-allele frequencies in the parental population, then the total score statistic can gain power relative to the NFS, by use of information on the deviations of parental-genotype frequencies from null expectations.

The two proposed statistics have some limitations. First, the FS could be biased by inappropriate assumptions on the parental-genotype distribution (e.g., random mating). In principle, serious departures from these assumptions could decrease the power of the NFS; this issue requires evaluation. The FS can also be biased by a failure to adjust for differences in ethnic distribution between the test families and the reference population. Comparison of FS and NFS provides a check on such bias; the presence of a statistically significant FS in the absence of a similar NFS would be grounds for suspicion. Finally, because the proposed statistics use more of the family data than do other statistics discussed in the Comparison with Other Statistics section, they are more complicated to compute. Software for use in the application of the statistics to data from nuclear families and from unrelated cases and controls is available from the authors.

The two statistics can be extended to multiallelic polymorphisms, to single and multiple markers in situations where the marker and disease locus is distinct from the marker(s) and where the recombination fractions and disequilibrium coefficients among them can be specified, and to more-complex family structures. Extension of the statistics to markers with m>2 alleles is conceptually straightforward, although notationally it is more cumbersome. Now the allele counts c_g are vectors of dimension m-1, the components of which represent the allele count for the ith allele, i=1,...,m-1, where the alleles are placed in arbitrary order and where the last allele is omitted. A family’s contributions to the nonfounder and founder scores are now vectors of dimension m-1, and their variances are (m-1)×(m-1) matrices.

The simulations done in the present study suggest that choosing c₁=1/2 for the heterozygote weight is more robust against model misspecification than is choosing either the dominant model c₁=1 or the recessive model c₁=0. When the disease locus is near the marker locus but is distinct from it, then there is another advantage to the specification c₁=1/2. For this choice, both the NFS and FS are independent of both the extent of gametic disequilibrium and the probability of recombination (θ) between trait and marker loci, and, thus, they have the same form, regardless of whether marker and trait loci coincide. This is not true of any choice c₁≠1/2, nor is it true of the total score statistic. For the latter, the factor 1-2θ determines the weight attached to the contribution from transmission disequilibrium in the offspring, relative to that from association in the parents’ genotypes. Misspecification of θ will not adversely affect the validity of the test statistic; however, it can decrease power by placing inappropriate weight on the parent-offspring transmission of the marker alleles.

Appendix A : Parental-Genotype Probabilities

We wish to describe the joint parental-genotype probabilities x_rs for the mother and father in a nuclear family, conditional on all genotype information observed for the family. To do so, suppose that the family contains n-2 offspring, the genotypes of which are summarized by the vector (n₁₁,n_12,n₂₂), where n_ij denotes the number of offspring with genotype B_iB_j, i, j=1, 2, and n₁₁+n₁₂+n₂₂=n-2. Let φ_rs(n₁₁,n₁₂,n₂₂)=φ_sr(n₁₁,n₁₂,n₂₂) denote the null probability of these genotypes when the parents have genotypes r and s. These probabilities are shown in the Genotype Probability for n Offspring column of Table 1.

If both the mother and the father have been typed with genotypes a and b, respectively, then

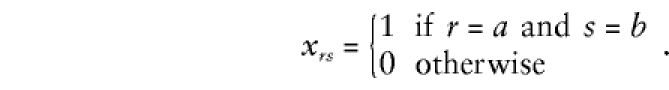If one parent (e.g., the mother) has been typed with genotype a, then

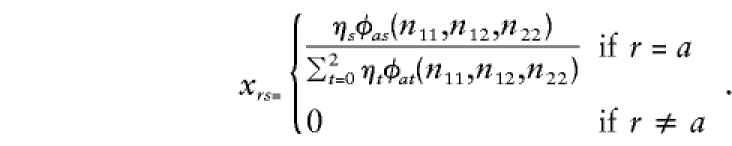In this instance, η_r is the prior probability that a parent has genotype r, r=0,1,2. If neither parent has been typed, then

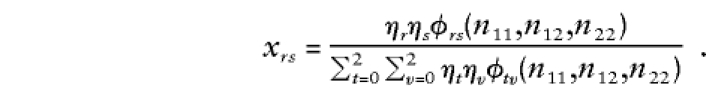The prior probabilities η₀,η₁,η₂ could be taken as the reference probabilities u₀,u₁,u₂, or they could be estimated from the data. To estimate them, we shall apply the method of maximum likelihood to all N families. To do so, we need to know each family's contribution to the likelihood—that is, the probability of the observed genotype data for the offspring and their parents. If the maternal and paternal genotypes are known to be a and b, respectively, then this probability is η_aη_bφ_ab(n₁₁,n₁₂,n₂₂). If one parent is known to have genotype a, then the contribution to the likelihood from this family is 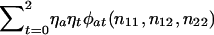. If neither parent has been typed, then the contribution is 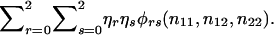The likelihood function is the product of the contributions from the N families. The maximum-likelihood estimates for η₀, η₁, and η₂ are the values that maximize this likelihood function.

Appendix B : Nonfounder and Founder Scores for One Family

In this section, we shall omit the family subscript ν.

Nonfounder score.—For a nuclear family typed at a single diallelic marker, the nonfounder score described in equation (11) of the companion article (Whittemore and Tu 2000) becomes

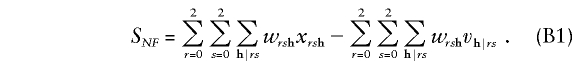Here r and s denote the maternal and paternal genotypes; h=(h₃,...,h_n) denotes the genotypes of the n-2 offspring; x_rsh is the conditional probability that the family genotypes are rsh, given the family-genotype information available; v_h|rs is the null probability of the offspring genotypes h, conditional on the parental genotypes r and s; and 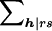denotes summation over all offspring genotypes compatible with parental genotypes r and s. Finally,

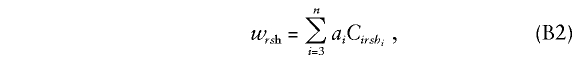where C_irshi is the expected allele count at the trait locus for offspring i, given the marker genotypes rsh for the family. Expression (B1) simplifies in the current application, wherein the trait and marker loci coincide. First, C_irshi=c_hi, so that (B2) becomes

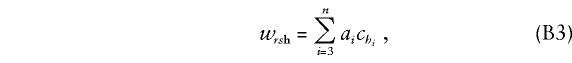which is independent of the parental genotypes. Moreover, since genotypes of the offspring are observed to be, for example, g₃,...,g_n, we have

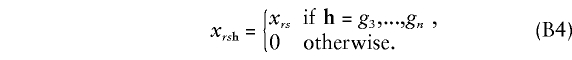Substitution of (B3) and (B4) into the first summand of (B1) and summing it over r and s gives the first summand as Σⁿ_i=3a_ic_gi. The independence of parental meioses implies that v_h|rs factors as

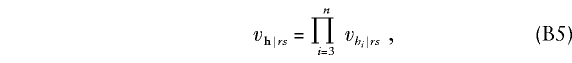where v_h|rs is the null probability that parents with genotypes r and s transmit genotype h to any offspring. Substitution of (B3), (B4), and (B5) into the second summand of (B1) gives the second summand as follows:

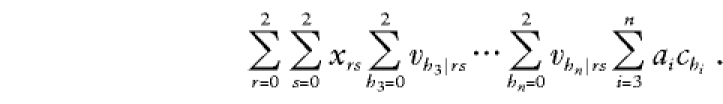After rearranging terms, this becomes aΣ²_r=0Σ²_s=0x_rsμ_rs, where 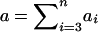is the total phenotype score for the offspring and where 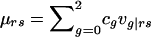is the expected genotype count for an offspring of parents with genotypes r and s. By combining the two summands of (B1) and by letting 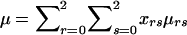denote the family’s expected offspring count, conditional on the genotype information available for the parents, we obtain the nonfounder score S_NF=Σⁿ_i=3a_ic_gi-aμ, in agreement with equation (2).

Founder score.—When trait and marker loci coincide and when the family consists of parents and offspring, the founder score described in equation (13) of the companion article (Whittemore and Tu 2000) is as follows:

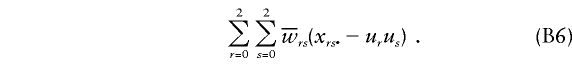Here u₀,u₁,u₂ denote the genotype frequencies in the reference population, and

Substitution of (B7) into (B6) gives expression (4).

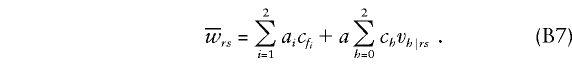Appendix C : Simulations

When the NFS is applied to typed sib pairs with untyped parents, the sibs’ genotypes serve two functions. First, they define one of the six family-genotype structures (FGSs) that determine six probability distributions for the unobserved parental genotypes. An FGS for a nuclear family consists of the number of offspring in the family plus the genotypes of all typed family members. For example, a sib pair with genotypes (g₁,g₂) and untyped parents has one of six possible FGSs, which correspond to the six possible sets {g₁,g₂}: {2,2}, {2,1}, {2,0}, { 1,1}, {1,0}, and {0,0}.

Second, when linked to the sibs’ phenotypes, the sibs’ genotypes contribute to the numerator of the NFS, which is conditioned on the FGS-specific parental-genotype distributions. To accommodate this conditioning, we performed the simulations in two nested steps. In step 1, we generated an FGS for each of the 100 families, and we then computed the corresponding 100 FGS-specific parental-genotype distributions, with use of the methods described in Appendix A. Each of the six FGSs determines a parental-genotype distribution.

In step 2, we generated sib genotypes for each family, conditional on its parental-genotype distribution and conditional on the sib phenotypes. Specifically, if a family had FGS=i and sib phenotypes y₁,y₂, where y_j=1 if the jth sib is affected and where y_j=0 otherwise, j=1,2, we generated sib genotypes g₁ and g₂, with the probability

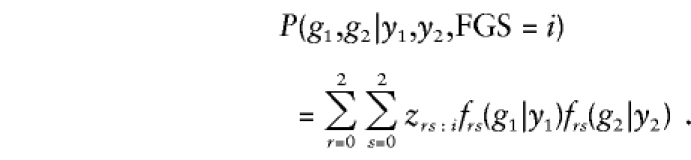In this instance, z_rs:i denotes the probability that the mother has genotype r and that the father has genotype s, given that the FGS is of type i, and f_rs(g_j|y_j) denotes the probability that a sib with phenotype y_j and with parents with genotypes r and s inherits genotype g_j, j=1,2. We then used these genotypes to compute the NFS for various choices of c₁ and ψ.

To evaluate the performance of the STDT statistic for affected-unaffected sib pairs, in step 2, we assigned one of the two genotypes of the ith FGS to the affected sib, and we assigned the other to the unaffected sib, with probabilities conditional on the sibs’ phenotypes. For each set of FGSs generated in step 1, step 2 was repeated 100 times. We then repeated step 1 (and its nested repetitions of step 2) for a total of T₁=10 times. Thus, for each sib-pair phenotype (discordant sib pairs and a mixture of discordant and affected sib pairs) and for each set of parameter values shown in table 4, we performed T₁×T₂=1000 trials. In each trial, we rejected the null hypothesis when a test statistic exceeded 3.09, which is the critical value for a one-tailed test of size α=.001.