Summary
Although it is clear that apoE plays an important role in the genetics of late-onset Alzheimer disease (AD), evidence exists that additional genes may play a role in AD, and estimates of the total contribution of apoE to the variance in onset of AD vary widely. Unfortunately, little information is available on the number and contribution of additional genes. We estimated the number of additional quantitative-trait loci and their contribution to the variance in age at onset of AD, as well as the contribution of apoE and sex, in an oligogenic segregation analysis of 75 families (742 individuals) ascertained for members with late-onset AD. We found evidence that four additional loci make a contribution to the variance in age at onset of late-onset AD that is similar to or greater in magnitude than that made by apoE, with one locus making a contribution several times greater than that of apoE. Additionally, we confirmed previous findings of a dose effect for the apoE ɛ4 allele, a protective effect for the ɛ2 allele, evidence for allelic interactions at the apoE locus, and a small protective effect for males. Furthermore, although we estimate that the apoE genotype can make a difference of ⩽17 years in age at onset of AD, our estimate of the contribution of apoE (7%–9%) to total variation in onset of AD is somewhat smaller than that which has previously been reported. Our results suggest that several genes that have not yet been localized may play a larger role than does apoE in late-onset AD.
Introduction
The search for novel genetic loci affecting liability for Alzheimer disease (AD [MIM 104300]) is proceeding, but there is little information on how many AD loci there may be. To date, four such genes have been conclusively identified. Three of these—APP, PS1, and PS2—have been linked to rare, autosomal dominant forms of AD that generally have an early onset (Goate et al. 1991; Schellenberg et al. 1992; Levy-Lahad et al. 1995a, 1995b; Sherrington et al. 1995). Only one, apoE, has been associated, in multiple studies, with common late-onset AD (Pericak-Vance et al. 1991; Saunders et al. 1993). The apoE gene has three alleles—ɛ2, ɛ3, and ɛ4—with the ɛ3 allele being most common. The ɛ4 allele has been associated with high risk for AD, relative to the ɛ3 allele, in a large number of studies (e.g., Corder et al. 1993; Jarvik et al. 1995; Levy-Lahad et al. 1998), whereas a smaller number of studies have reported evidence indicating that the less-common ɛ2 allele may have a protective effect (Corder et al. 1994; Jarvik et al. 1995). A number of other studies have not estimated an effect for the ɛ2 allele, since their sample sizes for this allele were small. Indeed, the protective effect for ɛ2 was confirmed in a reanalysis that combined a large number of individuals from multiple studies (Farrer et al. 1997).
Although most studies agree that genetic factors other than apoE play a role in late-onset AD, estimates of the relative contribution, to AD risk, of apoE versus these other factors vary widely. One study estimates that apoE accounts for 50% of the “predicted total genetic effect” (Roses et al. 1995), whereas others estimate that apoE accounts for 10%–15% of the total variance in age at onset (Bennett et al. 1995; Slooter et al. 1998). These different estimates may, in fact, be slightly closer together than they appear: the genetic variance (VG) is only a component of the total variance (VP). In a twin study, Bergem et al. (1997) estimated the heritability (narrow sense: VA /VP, where VA is the additive genetic variance) for AD to be 0.6. It is also possible to estimate, by use of the data of Bergem et al. (1997), that the fraction of the total genetic variance (broad sense: VG /VP) has a range of 0.76–0.83. However, since Bergem et al. (1997) do not allow for any censoring and since only a few years have passed since diagnosis of the discordant MZ twin pairs (Bergem and Lannfelt 1997), the broad-sense heritability could well be larger. These results indicate that ⩾30% of the total variance in AD—and possibly ⩾70%—is explained by unidentified genetic loci.
Clearly, 30%–70% is a large fraction of the total variance, but our ability to localize genes contributing to this variance will be determined by the number of such genes and by the contribution of each. If there is a single gene accounting for this variance, that gene should be fairly easy to localize. In fact, it would be surprising if such a single gene existed, since several complete genome screens (Pericak-Vance et al. 1998; Kehoe et al. 1999) have failed to produce any LOD scores >3 for such a gene. On the other hand, if there are many genes of small effect, localization of these genes may prove to be intractable. An estimate of the number of additional genes can give us an indication of how fruitful the search for additional AD genes will be.
In the present study, we estimated the number and effects of additional genes on age at onset of AD, by performing a Monte Carlo Markov chain (MCMC) oligogenic segregation analysis on a collection of families with late-onset AD. This study makes complete use of the available family data. The number of additional quantitative-trait loci (QTLs) involved in age at onset of AD and the relative contributions of each QTL to the variance in age at onset of AD were estimated, while both controlling for and estimating the effects of apoE and sex. Thus, the current analysis also provides a new estimate of the effects of apoE genotype, while controlling for the effects of the other genes and, at the same time, making complete use of the family data. Previously, most estimates of the effects of apoE have been from case-control studies or from family studies treated as case-control studies (Corder et al. 1993; Jarvik et al. 1995; Slooter et al. 1998). In such studies, it is impossible to account for the effects of other genes, since the individuals studied are unrelated (or are assumed to be so) and since other genes involved in late-onset AD have not been conclusively identified. Although our estimates of the effects of apoE have some similarities to previous estimates, we estimate that there are four QTLs, in addition to apoE, that have effects that are as large as or larger than those of apoE.
Subjects and Methods
Sample
Individuals in 75 families (including two Volga German families) with no known PS1, PS2, APP, or TAU mutations were evaluated either by the University of Washington Alzheimer's Disease Research Center, the Oregon Health Sciences University Alzheimer's Disease Center, or the University of Minnesota Alzheimer disease research group. Informed consent was obtained from all subjects. The families contained a total of 742 individuals, with a family-size range of 4–53 individuals. apoE genotypes were available for 419 individuals. Of these individuals, 203 had an age at onset of AD (affected), 201 had a censoring age at which they were last known to be free of AD (unaffected), and 15 had missing phenotype information. Individuals were considered to be missing phenotype data for this analysis if information on either age (age at onset of AD or censoring age) or affectation status was unavailable. Phenotypic data were available for 600 individuals, of whom 282 were affected and 318 were unaffected. Living affected individuals met published criteria for the clinical diagnosis of AD (McKhann et al. 1984). For deceased individuals without autopsies and for five families who were referred from outside our centers and who were not examined by our personnel, the diagnosis of probable AD was established on the basis of detailed medical records that often included consultations by neurologists, neuropsychological testing, computed tomography (CT) or magnetic-resonance imaging (MRI) of the brain, and laboratory testing excluding other causes of dementia. For the sample used here, the mean age at onset was 70.6±7.9 years, with an individual-onset range of 40–89 years. The range of mean onset within each individual family was 63–82 years, and 66 of the 75 families had at least one member with a case of AD confirmed at autopsy, with a total of 132 autopsies conducted in the families. Neuropathologic confirmation of the diagnosis met the criteria published by The Consortium to Establish a Registry for Alzheimer's Disease (CERAD; Mirra et al. 1991) and The Ronald and Nancy Reagan Research Institute of the Alzheimer's Association/National Institute on Aging Working Group (1998). apoE genotypes were determined by use of methods described elsewhere (Hixson and Vernier 1990).
Statistical Methods
To estimate the number of trait loci and the effects of each such locus, the effects of each apoE genotype, and the effect of sex on age at onset of AD, we applied the MCMC methods described elsewhere (Heath 1997; Daw et al. 1999). With the use of these methods, age at onset is modeled as a censored quantitative trait while an oligogenic segregation analysis is performed. Effectively, this is a survival analysis in which the failure curves for each covariate and genotypic group are cumulative normal distributions with the same variance. By using the term “covariate and genotypic group,” we mean to describe all individuals who share a particular multilocus genotype at all QTLs and who share a common value for each covariate. Such groups may also include individuals for whom the apoE genotype and other genetic data are probabilistically inferred from data on other family members. This inference effectively increases our sample size beyond the 419 individuals for whom apoE genotype is available. With use of this model, age at onset is given by: y=M+Xβ+Σki=1Qiαi+e, where M is the “baseline” age at onset, X is the incidence matrix for covariate effects (i.e., a matrix indicating the values at all the covariates; the entries for discrete covariates will be 0's or 1's), β is the vector of covariate effects, Qi is the incidence matrix for the effects of QTL i, αi is the vector of effects for QTL i, e is the normally distributed residual effect, and k is the number of QTLs currently estimated. All these parameters, with the exception of the elements of X determined by the data, are estimated by use of an MCMC process, as detailed elsewhere (Heath 1997; Daw et al. 1999). In brief, this process samples configurations of model parameters randomly but in such a way that these configurations are sampled with a frequency that is proportional to their posterior probability. Thus, after many iterations of this sampling process, the sampled model configurations provide an estimate of the posterior probability distribution over the space of possible parameter configurations. In the analyses presented here, this process was run for 500,000 iterations, and values from every 5th iteration were retained for estimation of posterior distributions.
Covariates of age at onset can be continuous (e.g., weight, height, and blood pressure) or discrete (e.g., sex, ethnic group, and country of birth), and they can include genotype at known genes or candidate genes. Such “genetic covariates” are useful because they allow the known mutation status to be used in the estimation of genotypic effects for a loci. Also, whereas the basic QTL model assumes that a locus is diallelic, a QTL modeled as a covariate can have any number of alleles. Furthermore, since the effect of each genotype at a genetic covariate is estimated independently, no restrictive assumptions are made with respect to allelic interactions at a genetic covariate locus. For example, the estimates of the effects of the apoE ɛ3/ɛ3 and apoE ɛ4/ɛ4 genotypes do not impose restrictions either on each other or on the estimate of the effect of the apoE ɛ3/ɛ4 genotype.
We also considered sex to be a covariate. An additive effect was estimated for males, with the female effect estimated as the baseline. In contrast to the apoE covariate, sex is a relatively simple covariate, with only two values and no missing data. As with the other effects, the sex effect was estimated to be an additive effect—that is, the years' difference between the average onset in males and that in females, after controlling for all other estimated effects.
In addition to providing estimates of the effects of sex and apoE, use of this MCMC method allows us to model the effects of additional genes that may contribute to AD. This not only gives us an estimate of the number of additional genes involved in late-onset AD, but it also gives us estimates of the effects of apoE while controlling for the additive effects of other genes and sex. All four possible models defined by sex and additional QTLs were considered: the effects of apoE genotypes on age at onset were estimated both with and without sex as a covariate and both with and without modeling of additional QTLs. In the analyses where additional QTLs were allowed, we estimated the variance attributed to each of these QTLs as well as the number of such QTLs. We then compared the variances of these QTLs to the variance estimated for apoE, to examine the effect sizes (i.e., the attributable phenotypic variance) for other putative late-onset AD genes and to examine the overall contribution of apoE to the variance of late-onset AD.
For purposes of comparison and for evaluation of our methods, a Kaplan-Meier survival analysis was done. Separate survival curves were computed for each apoE genotype. We were then able to compare these results both with the results that we obtained using the MCMC methods and with those obtained by other researchers using Kaplan-Meier survival analysis.
Results
Number of QTLs
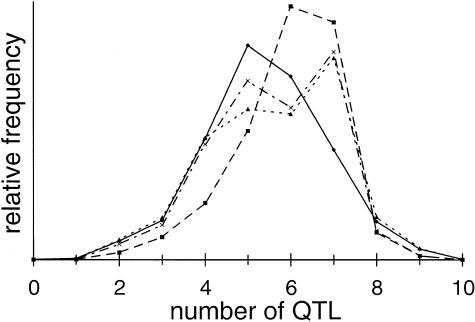
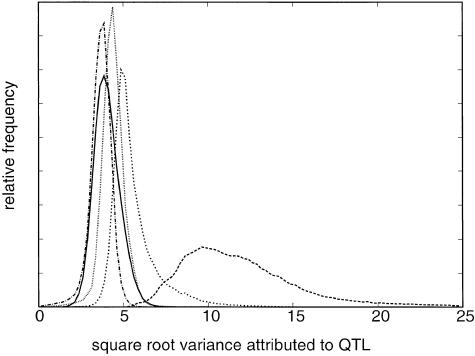
Our MCMC analysis of the 75 available families with late-onset AD found evidence for a number of genes, in addition to apoE, affecting age at onset of AD (table 1). The number of additional genes was estimated to be in the range of four to seven (fig. 1), with four of the QTLs generally having a variance that was as large as or larger than that of apoE. Of these four additional QTLs, one was substantially larger than the rest, accounting for >50% of the total genetic variance (fig. 2 and table 1). This largest QTL was estimated to be an overdominant locus—that is, the effect of the heterozygote genotype was estimated to be the most detrimental. The frequency of the common allele at this locus was estimated to be .60 (.07 SD), and, with the common homozygote fixed as baseline (zero effect), the heterozygote had an estimated effect of −7.8 years (3.0 SD) and the less-frequent homozygote had an estimated effect of +28.8 years (12.3 SD). The next three QTLs all had highly overlapping distributions, and they accounted for ∼13%, ∼8%, and ∼5% of the genetic variance (square-root variance ∼3.5–6 years). apoE accounted for 7%–9% of the genetic variance (square-root variance 4–4.5 years). Because of the overlap, we cannot exclude the possibility that the actual genes being modeled by the 2d-, 3d-, and 4th-largest QTLs are responsible for the same proportion of the actual trait variance as is apoE. The largest QTL, however, was clearly estimated to have larger variance than apoE, with the variance attributed to the largest QTL being greater than that attributed to apoE in >99.9% of the sampling iterations.
Table 1.
Partitioning of Variance of Age at Onset of AD
|
Percent of Total Variance (Square-Root Variance) Attributed to Effects Modeled |
||||
| Source of Variance | apoE, Sex, and Other QTLs | apoE and Other QTLs | apoE and Sex | apoE Only |
| Environment/residual | 1.5% (1.8 years) | 2.5% (2.5 years) | 84.7% (10.9 years) | 85.5% (10.9 years) |
| Sex | .7% (1.2 years) | … | .5% (.9 years) | … |
| Total genetic variance | 97.9% (14.8 years) | 97.5% (15.8 years) | 14.7% (4.5 years) | 14.5% (4.5 years) |
| apoE | 9.2% (4.5 years) | 6.6% (4.1 years) | 14.7% (4.5 years) | 14.5% (4.5 years) |
| Total variance, other QTLsa | 88.7% (14.1 years) | 90.9% (15.3 years) | … | … |
| 1stb | 57.1% (11.3 years) | 64.0% (12.7 years) | … | … |
| 2d | 13.5% (5.4 years) | 13.4% (5.8 years) | … | … |
| 3d | 8.1% (4.2 years) | 7.6% (4.4 years) | … | … |
| 4th | 5.7% (3.5 years) | 5.1% (3.6 years) | … | … |
| 5th | 3.1% (2.6 years) | 2.1% (2.3 years) | … | … |
| 6th | 1.4% (1.8 years) | .7% (1.4 years) | … | … |
| 7th | .4% (1.0 years) | .2% (.7 years) | … | … |
| Smaller QTLs | <.1% (.2 years) | <.1% (.3 years) | … | … |
| Total variance: | 224.4 | 256.6 | 140.1 | 138.5 |
Average total effect of all QTLs other than apoE.
Average effect of each QTL (other than apoE) ranked by effect size.
Figure 1.
The posterior distributions for the number of QTLs, in addition to apoE, affecting age at onset of AD. Distributions were generated in each of the four analysis runs in which additional QTL effects were modeled: 3 runs with apoE and other QTLs (run 1 [unbroken line with diamonds], run 2 [dashed line with squares], and run 3 [dotted line with triangles]) and 1 run with apoE, sex, and other QTLs (dashed and dotted line with X's).
Figure 2.
Posterior distributions for the phenotypic effect (square-root variance) attributed to apoE (unbroken line) and to each of the four largest QTLs (dotted lines and broken lines). Square-root variance is in years.
apoE Effects
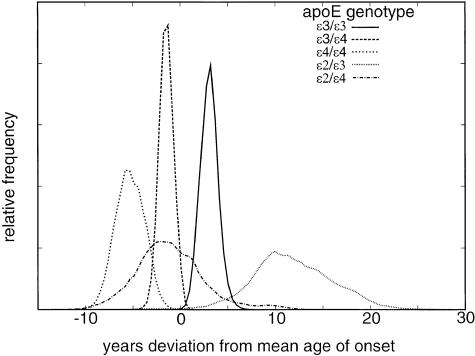
In addition to providing evidence for multiple QTLs, our analysis provides new estimates for the effects of each apoE genotype. These new estimates clearly confirm that apoE genotype affects age at onset of AD. The extreme genotypes—ɛ4/ɛ4 and ɛ2/ɛ3—differ in mean age at onset by ∼17 years (no individuals with the apoE ɛ2/ɛ2 genotypes were available in our data set) (table 2 and fig. 3). The apoE ɛ3 and ɛ4 alleles appear to act approximately additively, with the ɛ3/ɛ4 genotype falling approximately midway between the ɛ3/ɛ3 and ɛ4/ɛ4 genotypes. The ɛ2/ɛ3 genotype is clearly protective, relative to the other genotypes, with mean onset occurring 6–8 years later than that for the genotype ɛ3/ɛ3, which has the next oldest onset. The ɛ2/ɛ3 estimate has a large SD (4–5 years) as a result of the small number of such individuals in our sample. The SD for the ɛ2/ɛ4 genotypic effect is also large as a result of the small sample size. This latter distribution spans those for the ɛ4/ɛ4, ɛ3/ɛ4, and ɛ3/ɛ3 genotypes, although its mean is consistently placed between the ɛ3/ɛ4 and ɛ3/ɛ3 genotypic means. To which of these means the ɛ2/ɛ4 genotypic mean is nearest depends on whether the effects of additional QTLs are allowed: when no other genes are modeled, the ɛ2/ɛ4 genotype mean is estimated to be closer to the ɛ3/ɛ3 genotypic mean; when other genes are modeled, the ɛ2/ɛ4 genotype mean is estimated to be closer to the ɛ3/ɛ4 genotypic mean.
Table 2.
Means and SDs for Estimated Covariate Effects
|
Mean (SD) Estimated Covariate Effecta (years) |
||||||
| apoE Genotype |
||||||
| Effects Modeled | ɛ4/ɛ4 (n=111) | ɛ3/ɛ4 (n=207) | ɛ2/ɛ4 (n=67) | ɛ3/ɛ3 (n=19) | ɛ2/ɛ3 (n=15) | Male (n=331) |
| apoE, sex, other QTLs | −6.8 (1.3) | −1.6 (.7) | −.6 (3.4) | 4.2 (.9) | 10.0 (5.2) | 2.1 (1.2) |
| apoE, other QTLs | −5.3 (1.5) | −1.5 (.7) | −1.0 (3.7) | 3.1 (.9) | 11.8 (4.4) | … |
| apoE, sex | −6.3 (1.4) | −1.9 (.8) | 2.5 (3.7) | 3.8 (1.1) | 11.3 (4.0) | 1.3 (1.1) |
| apoE | −6.2 (1.4) | −2.0 (.8) | 2.3 (3.7) | 3.8 (1.1) | 11.2 (4.0) | … |
Of posterior distribution of effects, relative to sample mean.
Figure 3.
Posterior distributions for mean effect of each apoE genotype when the effects of other QTLs, but not the effect of sex, were modeled. Each curve is generated from 100,000 realizations consisting of every 5th of 500,000 iterations of the MCMC sampler.
Comparison of the results of our MCMC analysis of the effects of apoE on age at onset of AD (table 2) with results that we obtained from Kaplan-Meier survival analysis (table 3) showed that the two methods produced remarkably similar results. The years effect estimated by survival analysis was within one standard error of the effects estimated by use of MCMC methods for each genotype. The difference between the ɛ4/ɛ4 and ɛ2/ɛ3 genotypes was very slightly greater in the Kaplan-Meier analysis than in the MCMC analyses (18.2 years vs. 15.9–17.6 years). Although the results of the two methods of estimation of the effects of apoE are quite similar, the MCMC methods use all family data, can estimate many effects in addition to those of apoE, and can also be used to localize genes when marker data are available.
Table 3.
Kaplan-Meier Survival Analysis
| apoE Genotype |
|||||
| ɛ4/ɛ4 | ɛ3/ɛ4 | ɛ2/ɛ4 | ɛ3/ɛ3 | ɛ2/ɛ3 | |
| Mean age at onset | 71.2 | 75.2 | 77.3 | 81.2 | 89.4 |
| Effecta | −6.4 | −2.4 | −.3 | 3.6 | 11.8 |
| Standard error | (1.3) | (.7) | (2.8) | (1.3) | (4.8) |
Data represent deviation from overall mean.
Sex Effect
Sex also appears to affect age at onset of AD. The mean onset for males was estimated to be 1–2 years later than that for females, after accounting for other additive effects. Although this effect is small, the posterior probability that this effect is positive is 95%. The only discernible effect of the inclusion of sex was an increase in the difference between the ɛ3/ɛ3 and ɛ4/ɛ4 genotypes in the models allowing for the effects of other QTLs (table 2), suggesting an interaction between sex and apoE effects.
The estimated apoE effects were consistent across three MCMC-analysis runs of the same model. With use of a stochastic analysis method, such as the one used in the present study, an important issue is the stability of the results under different starting conditions. Table 4 shows the stability of the estimates of the effects of apoE in separate analysis runs of 500,000 iterations each, in which the effects of apoE genotype and other QTLs are modeled. The range of values between these runs is smaller for each effect than is the range between models shown in table 2. In particular, this indicates that the larger differences in apoE-genotype effects among models seen in table 2 are likely to reflect the different models, rather than the stochastic process (i.e., Monte Carlo error), although all the differences seen between models are within 1 SD of each other.
Table 4.
Effects of apoE Genotypes Estimated in Three Separate Analysis Runs Modeling apoE and Other QTL Effects
|
Mean (SD) Estimated Effect of apoE Genotypea (years) |
|||||
| Run | ɛ4/ɛ4 | ɛ3/ɛ4 | ɛ2/ɛ4 | ɛ3/ɛ3 | ɛ2/ɛ3 |
| 1 | −5.3 (1.5) | −1.5 (.7) | −1.0 (3.7) | 3.1 (.9) | 11.8 (4.4) |
| 2 | −5.4 (1.6) | −1.6 (.8) | −.6 (4.1) | 3.2 (1.1) | 11.4 (4.4) |
| 3 | −5.2 (1.6) | −1.3 (.8) | −1.2 (3.6) | 3.0 (1.2) | 10.7 (4.2) |
Of posterior distribution of effects, relative to sample mean.
The estimate of the number of QTLs appears to be more variable (fig. 1), but the estimates of the effect sizes for the largest four QTLs were consistent in iterations with ⩾4 QTLs present. The remaining QTLs all tended to have a smaller effect than did apoE and, in some cases, the effect was very small. In iterations with seven QTLs, for example, the effects attributed to the two smallest QTLs modeled are probably too small to be detectable in linkage analyses of this data. Some of these smaller QTLs may be artifacts of the MCMC analysis process. In any case, in all runs, the posterior probability of the presence of four to seven additional QTLs was greater than the posterior probability of the presence of any other number of QTLs.
Discussion
Our analysis of familial late-onset AD data provides novel evidence that four additional genes make a contribution to age-at-onset variation that is as large as or larger than that of apoE. This analysis also provides new estimates of the effects of sex and each apoE genotype. Our estimates of the relative direction of the effects of apoE genotypes and sex confirm previous findings and thus support the use of MCMC methods. However, our estimate of the proportion of the total variance attributed to apoE appears to be slightly smaller than previously reported estimates and places new emphasis on the role that additional genes may play in late-onset AD.
The results from our oligogenic model suggest that ⩾4 additional QTLs may each account for at least as much of the variability in age at onset of AD as does apoE. The true number of genes cannot be precisely estimated: multiple genes with similar effects segregating in different families can produce evidence for a single gene with a larger effect; some other effects, such as transmissible environment effects, could potentially mimic genes. Also, an astute reader will have noticed that, in table 1, the total variance estimated is different, depending on whether additional QTLs are modeled. This difference is caused in part by underestimation of the total phenotypic variance, under the data-censoring model, when additional QTLs are not allowed. Underestimation occurs because, when additional QTLs are not modeled, the trait values for censored individuals are constrained to be near those of uncensored individuals, by the assumption of normality in the residual variance. The difference in total variance seen in the two cases is similar to the difference that one would see between estimation of total variance in a sample including only cases and estimation of total variance in a mixed sample that is more representative of the whole population. In addition, the residual variance in the oligogenic analyses may be underestimated. In data collection, only families with multiple affected individuals were ascertained, which could bias the estimate of the environmental variance downward.
The overdominance estimated in the largest QTL could result from a number of factors. The QTL could, in fact, be overdominant. If this were the case, caution would be suggested in the use of methods that have high power only for modes of inheritance in which the heterozygote falls between the two homozygotes. Another possibility is that gene-gene interactions might result in estimation of an overdominant effect. The degree to which this is a problem for gene localization will depend on the degree of the interaction. An additional genetic reason for estimation of overdominance could be the presence of multiple alleles at the trait locus. The model used here allowed for only two alleles at a QTL, so if the actual trait locus has three or more alleles with different effects, as is the case for apoE, the diallelic model could cause an overdominant trait to be estimated. Finally, the results of a previous study (Daw et al. 1999), showed some overdominance as a result of trait-model overfitting. This overfitting was not detrimental to localization of genes.
It might seem surprising that a QTL with the effect of the largest QTL found here has not already been localized. If this QTL does in fact exist, there could be a number of reasons why it has not yet been found. For a simple overdominant trait—that is, a monogenic diallelic trait where the heterozygotes are affected but the homozygotes are not affected—with a 60% frequency for the common allele, the expected identity-by-descent allele sharing at the disease locus between affected siblings is ∼1.3. We believe that the trait is far more complex than this simple overdominant model, and complications such as the presence of multiple alleles at the trait locus, the interactions between those alleles, the presence of other trait loci, and the nongenetic influences on the trait would all tend to reduce this already modest identity-by-descent sharing. Thus, to detect such a locus, marker-allele sharing methods may require a sample far larger than any that have been collected to date. Alternatively, LOD-score methods depend on a model for the disease locus and are known to perform poorly when the model is wrong. Overdominant models are not generally considered when LOD-score linkage analysis is done. If the locus identified here exists, the models used previously may have resulted in low power to detect linkage.
There are several approaches that may be able to localize this trait locus. When we restrict these MCMC methods to prevent them from searching outside the traditional dominant-to-recessive range, these methods have greater difficulty in identification of the putative QTL reported here (data not shown). Although a multiallelic model with interactions could be the true model, it is possible that a single-locus overdominant model will fit the data sufficiently well to localize the gene. When analyzing complex traits, LOD-score methods may benefit from the consideration of a wider range of trait-locus models. Variance component methods, which estimate additive and dominance components for a locus, might also be able to localize such a complex locus. We expect that trait loci detected by means of segregation analysis with use of these MCMC methods can also be localized by means of combined segregation and linkage analysis with these methods.
Our results for the apoE genotypic effects confirmed the generally accepted findings of a dose effect for the ɛ4 allele with respect to the ɛ3 allele (Corder et al. 1993) and also found shifts in age at onset of AD that correspond exactly to the order of the liabilities for AD for each genotype found in some previous studies (Jarvik et al. 1995; Farrer et al. 1997). Consistent with the results of previous reports (Corder et al. 1994), we found that the ɛ2/ɛ3 genotype has a strong protective effect. However, the mean of the posterior distribution for the ɛ2/ɛ4 genotypic effect was found to be between that of ɛ3/ɛ3 and ɛ3/ɛ4 in all our analyses, suggesting that the protective effect of the ɛ2 allele may be largely overcome by the detrimental effect of the ɛ4 allele. Unfortunately, the large overlap that occurs in the distributions of the ɛ3/ɛ4 and ɛ3/ɛ3 genotypes indicates that a sample of families including a larger number of individuals with the ɛ2/ɛ4 genotype than the number seen in the present study is required to resolve the relative effect of this genotype. Additional difficulties in obtaining an estimation of the ɛ2/ɛ4 effect may arise if there are interactions with other loci or if there is linkage disequilibrium with other sites either in or near apoE. Such interactions are suggested by the observation that the mean for ɛ2/ɛ4 is closer to that of ɛ3/ɛ4 when other QTLs are included in the model and that the mean for ɛ2/ɛ4 is closer to ɛ3/ɛ3 when other QTLs are not included. Since previous methods of analysis have not explicitly incorporated additional QTLs into the analysis, this observation of evidence for interactions between apoE and other factors is new. Results described elsewhere (Roses et al. 1994) have shown a difference similar to that found in the present study, with regard to median age at onset for the different apoE genotypes. The difference between the ɛ4/ɛ4 and ɛ2/ɛ3 genotypes found by Roses et al. (1994) was slightly >15 years, which is very close to our finding. This agreement with the results of previous studies increases the confidence in these and other estimates of the effects of apoE, even though other studies did not use full pedigree data, as was done in the present study.
Allelic interaction between ɛ2 and the other apoE alleles is suggested by the results of the present study. Unfortunately, we could not estimate the effects of the ɛ2/ɛ2 genotype, since there were neither any sampled individuals with the ɛ2/ɛ2 genotype nor any individuals in whom this genotype could be clearly inferred. However, the placement of the ɛ2/ɛ3 and ɛ2/ɛ4 effects, relative to the placement of other effects, suggests that the ɛ2 allele does not interact additively with both the ɛ3 and ɛ4 alleles. In a strictly additive system, one would expect either the protective effect of the ɛ2/ɛ3 genotype to be smaller or the ɛ2/ɛ4 genotype to have a larger mean than the ɛ3/ɛ3 genotype. Since these results suggest allelic interaction, in the search for additional AD genes, it may be important to account for apoE genotype, as is done here, rather than use a model based on the simple presence or absence of each of the alleles.
While some previous discussion has focused on whether apoE is a causative locus or a modifier locus for AD, this distinction may be semantic and is irrelevant under the model used here. Our model assumes that everyone will eventually get AD if they live long enough and that the QTLs simply shift the mean age at onset—that is, a highly protective genotype would be modeled as shifting the mean age at onset to a much later age. The ramifications and limitations of this model are discussed elsewhere (Daw et al. 1999). With a disease that occurs as late in life as does late-onset AD, there is no question that the difference of 16–17 years found between the ɛ4/ɛ4 and ɛ2/ɛ3 genotypes represents an important factor in AD liability. Delaying the onset by even as much as a few years would greatly reduce the number of clinical AD cases.
Finally, we confirmed evidence for a protective effect for AD in males. Such a protective effect is consistent with findings from previous studies (Payami et al. 1994; Gao et al. 1998). Although this effect was relatively small (1–2 years), sex could interact with other risk factors, thereby making it more significant in some situations than in others. The precision of the estimates of covariate effects (sex and apoE in the present study) is affected by the number sampled in each covariate group, and the estimates of these effects, relative to the mean, are also affected by the number in each group. However, different numbers in each group do not bias the estimates of the effect of each covariate group relative to each other. For example, the estimate of the male effect versus the female effect is not biased by different numbers of male and female family members sampled. In addition, the estimates are not biased on the basis of whether family members are unaffected or have observed ages of onset, since the censored-data model used (Daw et al. 1999) accounts for this. The differences seen in the estimates of the apoE effects, in a comparison of the model including apoE, sex, and other QTLs with the model including just apoE and other QTLs, suggest an interaction between apoE genotype and sex. This finding is consistent with previously reported results for the risk of AD in a case-control study (Jarvik et al. 1995).
Although these results clearly confirm the important role of apoE in late-onset familial AD, they also suggest that apoE represents only 7%–9% of the total variance in age at onset of familial AD and that it is but one of several important genes. There appear to be ⩾4 additional QTLs that have an effect, at least on a par with that of apoE, on age at onset of familial AD. One of these QTLs appears to have a much greater effect. These results indicate that MCMC methods should be able to localize several novel late-onset AD loci, once a full-genome screen is completed on this data set.
Acknowledgments
Research supported by National Institutes of Health grants AG 05136, GM 46255, and AG 08017 and by Alzheimer's Association grant RG1-96-042.
Electronic-Database Information
Accession number and URL for data in this article are as follows:
- Online Mendelian Inheritance in Man (OMIM), http://www.ncbi.nlm.nih.gov/Omim/ (for AD [MIM 104300]) [PubMed]
References
- Bennett C, Crawford F, Osborne A, Diaz P, Hoyne J, Lopez R, Roques P, et al (1995) Evidence that the APOE locus influences rate of disease progression in late-onset familial Alzheimer's-disease but is not causative. Am J Med Genet 60:1–6 [DOI] [PubMed]
- Bergem ALM, Engedal K, Kringlen E (1997) The role of heredity in late-onset Alzheimer disease and vascular dementia: a twin study. Arch Gen Psychiatry 54:264–270 [DOI] [PubMed]
- Bergem ALM, Lannfelt L (1997) Apolipoprotein E type ɛ4 allele, heritability and age at onset in twins with Alzheimer disease and vascular dementia. Clin Genet 52:408–413 [DOI] [PubMed]
- Corder EH, Saunders AM, Risch NJ, Strittmatter WJ, Schmechel DE, Gaskell PC Jr, Rimmler JB, et al (1994) Protective effect of apolipoprotein E type 2 allele for late onset Alzheimer disease. Nat Genet 7:180–184 [DOI] [PubMed]
- Corder EH, Saunders AM, Strittmatter WJ, Schmechel DE, Gaskell PC, Small GW, Roses AD, et al (1993) Gene dose of apolipoprotein E type 4 allele and the risk of Alzheimer's disease in late onset families. Science 261:921–923 [DOI] [PubMed]
- Daw EW, Heath SC, Wijsman EM (1999) Multipoint oligogenic analysis of age-at-onset data with applications to Alzheimer disease pedigrees. Am J Hum Genet 64:839–851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farrer LA, Cupples LA, Haines JL, Hyman B, Kukull WA, Mayeux R, Myers RH, et al (1997) Effects of age, sex, and ethnicity on the association between apolipoprotein E genotype and Alzheimer disease: a meta-analysis: APOE and Alzheimer Disease Meta Analysis Consortium. JAMA 278:1349–1356 [PubMed]
- Gao S, Hendrie HC, Hall KS, Hui S (1998) The relationships between age, sex, and the incidence of dementia and Alzheimer disease: a meta-analysis. Arch Gen Psychiatry 55:809–815 [DOI] [PubMed]
- Goate A, Chartier-Harlin MC, Mullan M, Brown J, Crawford F, Fidani L, Giuffra L, et al (1991) Segregation of a missense mutation in the amyloid precursor protein gene with familial Alzheimer's disease. Nature 349:704–706 [DOI] [PubMed]
- Heath SC (1997) Markov chain Monte Carlo segregation and linkage analysis for oligogenic models. Am J Hum Genet 61:748–760 [DOI] [PMC free article] [PubMed]
- Hixson JE, Vernier DT (1990) Restriction isotyping of human apolipoprotein E by gene amplification and cleavage with HhaI. J Lipid Res 31:545–548 [PubMed]
- Jarvik GP, Wijsman EM, Kukull WA, Schellenberg GD, Yu C, Larson EB (1995) Interactions of apolipoprotein E genotype, total cholesterol level, age, and sex in prediction of Alzheimer's disease: a case-control study. Neurology 45:1092–1096 [DOI] [PubMed]
- Kehoe P, Wavrant-De Vrieze F, Crook R, Wu WS, Holmans P, Fenton I, Spurlock G, et al (1999) A full genome scan for late onset Alzheimer's disease. Hum Mol Genet 8:237–245 [DOI] [PubMed]
- Levy-Lahad E, Tsuang D, Bird TD (1998) Recent advances in the genetics of Alzheimer's disease. J Geriatr Psychiatry Neurol 11:42–54 [DOI] [PubMed]
- Levy-Lahad E, Wasco W, Poorkaj P, Romano DM, Oshima J, Pettingell WH, Yu CE, et al (1995a) Candidate gene for the chromosome 1 familial Alzheimer's disease locus. Science 269:973–977 [DOI] [PubMed]
- Levy-Lahad E, Wijsman EM, Nemens E, Anderson L, Goddard KA, Weber JL, Bird TD, et al (1995b) A familial Alzheimer's disease locus on chromosome 1. Science 269:970–973 [DOI] [PubMed]
- McKhann G, Drachman D, Folstein M, Katzman R, Price D, Stadlan EM (1984) Clinical diagnosis of Alzheimer's disease: report of the NINCDS-ADRDA Work Group under the auspices of Department of Health and Human Services Task Force on Alzheimer's Disease. Neurology 34:939–944 [DOI] [PubMed]
- Mirra SS, Heyman A, McKeel D, Sumi SM, Crain BJ, Brownlee LM, Vogel FS, et al (1991) The Consortium to Establish a Registry for Alzheimer's Disease (CERAD): Part II. Standardization of the neuropathologic assessment of Alzheimer's disease. Neurology 41:479–486 [DOI] [PubMed]
- Payami H, Montee KR, Kaye JA, Bird TD, Yu CE, Wijsman EM, Schellenberg GD (1994) Alzheimer's disease, apolipoprotein E4, and gender. JAMA 271:1316–1317 [PubMed]
- Pericak-Vance MA, Bass MP, Yamaoka LH, Gaskell PC, Scott WK, Terwedow HA, Menold MM, et al (1998) Complete genomic screen in late-onset familial Alzheimer's disease. Neurobiol Aging 19:S39–S42 [DOI] [PubMed]
- Pericak-Vance MA, Bebout JL, Gaskell PC Jr, Yamaoka LH, Hung W-Y, Alberts MJ, Walker AP, et al (1991) Linkage studies in familial Alzheimer disease: Evidence for chromosome 19 linkage. Am J Hum Genet 48:1034–1050 [PMC free article] [PubMed]
- Ronald and Nancy Reagan Research Institute of the Alzheimer's Association and the National Institute on Aging Working Group, The (1998) Consensus Report of the Working Group on: "Molecular and Biochemical Markers of Alzheimer's Disease." Neurobiol Aging 19:109–116 [PubMed]
- Roses A, Devlin B, Conneally PM, Small G, Saunders AM, Pritchard M, Locke PA, et al (1995) Measuring the genetic contribution of APOE in late-onset Alzheimer disease. Am J Hum Genet Suppl 57:A202 [Google Scholar]
- Roses AD, Strittmatter WJ, Pericak-Vance MA, Corder EH, Saunders AM, Schmechel DE (1994) Clinical application of apolipoprotein E genotyping to Alzheimer's disease. Lancet 343:1564–1565 [DOI] [PubMed]
- Saunders AM, Strittmatter WJ, Schmechel D, St George-Hyslop PH, Pericak-Vance MA, Joo SH, Rosi BL, et al (1993) Association of apolipoprotein E allele ɛ4 with late-onset familial and sporadic Alzheimer's disease. Neurology 43:1467–1472 [DOI] [PubMed]
- Schellenberg GD, Bird TD, Wijsman EM, Orr HT, Anderson LL, Nemens E, White JA, et al (1992) Genetic linkage evidence for a familial Alzheimer's disease locus on chromosome 14. Science 258:668–671 [DOI] [PubMed]
- Sherrington R, Rogaev EI, Liang Y, Rogaeva EA, Levesque G, Ikeda M, Chi H, et al (1995) Cloning of a gene bearing missense mutations in early-onset familial Alzheimer's disease. Nature 375:754–760 [DOI] [PubMed]
- Slooter AJC, Cruts M, Kalmijn S, Hofman A, Breteler MMB, Van Broeckhoven C, van Duijn CM (1998) Risk estimates of dementia by apolipoprotein E genotypes from a population-based incidence study: the Rotterdam Study. Arch Neurol 55:964–968 [DOI] [PubMed]