Summary
Most noninfectious disease is caused by low-penetrance alleles interacting with other genes and environmental factors. Consider the simple setting where a diallelic autosomal candidate gene and a binary exposure together affect disease susceptibility. Suppose that one has genotyped affected probands and their parents and has determined each proband's exposure status. One proposed method for assessment of etiologic interaction of genotype and exposure, an extension of the transmission/disequilibrium test, tests for differences in transmission of the variant allele from heterozygous parents to exposed versus unexposed probands. We show that this test is not generally valid. An alternative approach compares the conditional genotype distribution of unexposed cases, given parental genotypes, versus that of exposed cases. This approach provides maximum-likelihood estimators for genetic relative-risk parameters and genotype-exposure–interaction parameters, as well as a likelihood-ratio test (LRT) of the no-interaction null hypothesis. We show how to apply this approach, using log-linear models. When a genotype-exposure association arises solely through incomplete mixing of subpopulations that differ in both exposure prevalence and allele frequency, the LRT remains valid. The LRT becomes invalid, however, if offspring genotypes do not follow Mendelian proportions in each parental mating type—for example, because of genotypic differences in survival—or if a genotype-exposure association reflects an influence of genotype on propensity for exposure—for example, through behavioral mechanisms. Because the needed assumptions likely hold in many situations, the likelihood-based approach should be broadly applicable for diseases in which probands commonly have living parents.
Introduction
Many diseases are neither purely genetic nor purely environmental but arise through the joint action of genetic susceptibilities and environmental factors. In the study of such diseases, a natural goal is to understand how genetic makeup and exposure history work together to influence susceptibility. Toward that end, interest often focuses on possible synergism—that is, on assessment of whether the effect of genotype on risk changes with exposure level or, equivalently, whether the effect of exposure on risk changes with genotype.
Whether synergism exists can depend on how effects are measured. What qualifies as synergism when effects are assessed, for example, as differences in penetrances may fail to qualify when effects are measured as ratios of penetrances. Thus, when an environmental agent has some effect on risk for every genotype, the measurement scale can govern whether the magnitude of that effect differs among genotypes. Proposed methods for evaluation of genotype-exposure interaction start from a basic model in which the focus is on the relative risk of disease (i.e., the ratio of penetrances) for those with versus those without a particular genotype. Under such models, interaction with exposure is assessed by determining whether the genotype relative risks vary across levels of the exposure. We adopt this statistical definition of interaction, recognizing that it need not correspond to biological interaction (Greenland and Rothman 1998).
For the study of genetic effects, designs based on the genotyping of affected individuals and their parents are highly informative and offer robustness against spurious conclusions induced by hidden genetic structure, such as stratification or admixture. Linkage disequilibrium can be detected by studying heterozygous parents and comparing their rate of transmission of the variant allele with the null value .5, by use of the transmission/disequilibrium test (TDT [Spielman et al. 1993; Spielman and Ewens 1996]). Alternatively, one can compare the genotype distribution of cases versus that expected given their parents' genotypes, by using likelihood-based tests (Self et al. 1991; Schaid and Sommer 1993; Weinberg et al. 1998) or other tests (Flanders and Khoury 1996). Log-linear modeling allows implementation of such likelihood-based analyses of case-parent data and can be extended to examine prenatal effects of maternal genotype and imprinting effects, in addition to effects of inherited genotype on risk (Weinberg et al. 1998; Wilcox et al. 1998; Weinberg 1999b). In addition, data from incomplete triads can be incorporated efficiently (Weinberg 1999a). All these methods share robustness against population structure. They all rely on a key, but often reasonable, assumption that transmission of alleles from parents to offspring follows Mendelian probabilities and that, for each parental mating type, the Mendelian genotype proportions persist among offspring until the ages at which the probands are studied.
Case-parent designs are also useful for studying the joint effects of candidate genes and exposures. Various authors have proposed examination of genotype-exposure interaction by the grouping of case-parent triads according to the exposure status of the case and testing for differences between exposed and unexposed groups. These proposals fall into two types: some, extending the TDT, have used as the basis of comparison the rates of transmission of the variant allele from heterozygous parents to affected offspring (Harley et al. 1995; Maestri et al. 1997; Schaid 1999a); others have used the genotype distribution of cases, given their parents' genotypes (Khoury 1994; Khoury and Flanders 1996; Schaid 1999a; Witte et al. 1999). Recently, Schaid (1999a) studied the power of both types of methods for testing for genotype-exposure interaction in populations without hidden genetic structure.
The purpose of this paper is threefold. First, we show that tests for genotype-exposure interaction that are based on comparison of allelic transmission rates are not generally valid. Second, we describe log-linear models for studying the joint effects of genetics and exposure on risk. For simplicity, we restrict attention to a dichotomous disease trait in relation to a diallelic autosomal candidate gene and a two-level exposure. This log-linear approach is valid for assessing the genotype effects and gene-exposure–interaction effects under certain assumptions about the population under study. Exposure effects cannot usually be estimated with case-parent data. Third, we point out some potential pitfalls in the interpretation of evidence that favors gene-environment interaction and that arises from case-parent designs, and we examine whether tests of fit are helpful in the detection of violations of assumptions.
Notation
Consider a diallelic autosomal candidate gene with one allele designated as the variant allele. Let M, P, and C denote the number of copies of the variant allele carried by the mother, father, and child, respectively, each of which can take values 0, 1, or 2. Let E denote exposure status, which, for simplicity, we take to have two levels, with values 0 or 1 for triads in which the case is unexposed or exposed, respectively. We assume symmetry of mating, so that, for example, (M,P)=(1,2) has the same probability of occurring in the population as does (M,P)=(2,1). Under this assumption, and ignoring possible maternal or imprinting effects on risk, we can treat symmetric pairs such as these as a single joint parental genotype. This pairing gives 6 distinct parental mating types, 3 of which are informative, and 10 distinct categories of (M,P,C), 7 of which are informative (Schaid and Sommer 1993). With a binary exposure, the triads under study can be partitioned into 20 distinct categories (14 informative) based on M, P, C, and E.
Let τ be the transmission rate (the probability that a heterozygous parent transmitted the variant allele, given that the offspring became affected); we use τE and τU when distinguishing between exposed and unexposed offspring, respectively. Let Rc (c=1 or 2) be the relative risk of disease for a person with c copies of the variant allele, compared with a person with no copies; we use REc and RUc when distinguishing between exposed and unexposed persons, respectively. The term “transition ratio” will denote a ratio of conditional probabilities P(C=c|M,P)/P(C=c*|M,P), where c* denotes the fewest copies of the variant allele that are possible for an offspring from the given parental-mating type.
Transmission-Based Approach
One straightforward approach for assessment of interaction, a natural extension of the TDT, looks for differences in transmission rates from heterozygous parents to exposed versus unexposed probands. The method construes the equal-transmission-rate null hypothesis H0:τE=τU as an appropriate no-interaction null (Schaid 1999a) and tests it by using either the usual χ2 test for comparing the two proportions or Fisher's exact test. A related transmission-based conditional logistic-regression procedure has been used by Maestri et al. (1997) and was originally proposed by Harley et al. (1995) in a somewhat different context. Two problems invalidate these approaches—that is, make their type I error rates depart from nominal values.
First, when the variant allele affects risk, transmission rates can differ between exposed and unexposed triads even if exposure has no effect at all on risk, either alone or in concert with the variant allele. In other words, the correct no-interaction null hypothesis—namely, H0:REc=RUc for c=1 and 2—is not equivalent to the equal-transmission-rate null hypothesis actually being tested—namely, H0:τE=τU. This nonequivalence arises from a particular kind of hidden population structure. Ignoring exposure for the moment, one finds that the transmission rate from a heterozygous parent depends on the relative risks R1 and R2 and on the distribution of mating types in the sampled population. Three mating types contribute information about transmissions from heterozygous parents—namely, (1,2), (1,1), and (0,1). Table 1 shows how to calculate the transmission rate as a weighted average of mating-type–specific transmission rates, in which the weights depend on the relative frequencies of the mating types. If one assumes that the variant allele confers some risk—that is, Rc≠1 for some c—then transmission rates will differ across mating types (table 1). Only in the unlikely circumstance that R2=R21 will transmission rates for the three informative mating types be the same. Now consider a structured population in which both the frequency of the variant allele and the exposure prevalence differ among subpopulations in such a way that, in the general population, exposure is correlated with presence of the variant allele. In this situation, weights based on the relative frequencies of the mating types can differ between exposed and unexposed triads. This difference in weights can induce a difference in exposure-specific transmission rates even when the risk parameters R1 and R2 are the same for exposed and for unexposed individuals. In this way, transmission rates from heterozygous parents to exposed versus unexposed probands can differ even under the no-interaction null hypothesis. (One can also concoct scenarios in which interaction exists but transmission rates to exposed and to unexposed probands are equal.)
Table 1.
Rate of Transmission of Variant Allele from Heterozygous Parents, as a Weighted Average of Mating-Type–Specific Transmission Rates across Informative Mating Types
| Informative ParentalMating Type | Proportion of Parents (of Cases) with Given Mating Typea | Proportion of Heterozygous Parents (of Cases) with Given Mating Type | Mating-Type–SpecificTransmission Rate |
| (1,2) | π12 | π12/π12+2π11+π01=w12 | R2/R1+R2 |
| (1,1) | π11 | 2π11/π12+2π11+π01=w11 | R2+R1/R2+2R1+1 |
| (0,1) | π01 | π01/π12+2π11+π01=w01 | R1/1+R1 |
| Weighted averageb | w12 R2/R1+R2+w11 R2+R1/R2+2R1+1+w01 R1/1+R1 |
Under the assumption of mating symmetry, the conditional probability that parents have the given mating type, given that their child is affected; that is πij=P[(M,P)=(i,j) or (j,i)∣D].
This weighted average equals the transmission rate.
As an example in which no interaction exists but transmission rates are unequal, consider a population that consists of two subpopulations each in Hardy-Weinberg equilibrium: one, in which the frequency of the variant allele and the exposure frequency are each .9, constitutes 50% of the population; and a second, in which allele frequency and exposure prevalence are each .1, makes up the remaining 50%. For each subpopulation, assume that exposure does not affect risk and that RE2=RU2=3 and RE1=RU1=1 (recessive, no interaction). Also assume that both subpopulations have the same background risk for unexposed individuals without the variant allele. Then, among triads with exposed probands, mating types (1,2), (1,1), and (0,1) occur in proportions .214, .020, and .013, respectively, whereas, among triads with unexposed probands, they occur in proportions .055, .041, and .223, respectively. The resulting transmission rates are τE=.73 and τU=.58. This difference has nothing whatsoever to do with genotype-exposure interaction, but it will increase, beyond its nominal value, the type I error rate of the transmission-based test of interaction. The genotype-exposure correlation is crucial: if either exposure prevalence or allele frequency were the same in both subpopulations, eliminating the correlation, τE and τU would be the same. This example shows that H0:τE=τU cannot be regarded as equivalent to the no-interaction null hypothesis, H0:REc=RUc for c=1 and 2, when a structured population is under study.
A second problem invalidates the method even when population structure is benign: the test based on transmission rates assumes that transmissions from heterozygous parents are independent events, when, in general, they are not. The dependency arises because triads are ascertained conditional on the offspring's being affected. When both parents of a diseased child are heterozygous, the probability that the mother transmitted the variant allele, given that the father did, is R2/(R1+R2), whereas the probability that the mother transmitted the variant allele, given that the father did not, is R1/(R1+1). These two probabilities differ, thus ruling out independence, except in two special cases: first, when the variant allele has no effect on risk itself and is not in linkage disequilibrium with another susceptibility locus (i.e., R2=R1=1); and, second, when R2=R21. This nonindependence means that the test statistic will generally not have a χ2 distribution under the equal-transmission-rate null hypothesis, nor will it have a noncentral χ2 distribution under alternatives, a fact that has not been fully appreciated. Note the contrast to the TDT, in which, under its null hypothesis that the allele is unrelated to risk, transmissions from heterozygous parents are independent (although nonindependence can arise under alternative hypotheses and can render the noncentral χ2 distribution inappropriate).
To illustrate how these two problems can affect the type I error rate, we carried out simulation experiments, using, in each, 10,000 replications of a study involving 1,000 case-parent triads. Simulations were programmed in GAUSS (Aptech Systems). For the population mentioned earlier, in which transmission rates were unequal under the no-interaction null hypothesis, the usual χ2 test with nominal size .05 had an empirical type I error rate of .474 with a simulation SE of .005. Thus, the two problems together induced a dramatically larger-than-nominal type I error rate in this example. Lack of independence alone can induce either a larger- or a smaller-than-nominal significance level. For a population in Hardy-Weinberg equilibrium, with allele frequency and exposure prevalence each .5 and RE2=RU2=3 and RE1=RU1=1, as before, the empirical type I error rate was .067 with SE .0025 for a χ2 test with nominal size .05. Retaining the same population characteristics except that RE2=RU2= 1/3 and repeating the simulation yielded an empirical type I error rate of .036 with SE .0019. Such effects on type I error rate arise in any analyses of interaction that are based on the counting of transmissions from heterozygous parents, including the conditional logistic-regression approaches of Harley et al. (1995) and Maestri et al. (1997). The magnitude of such effects can change substantially with different subpopulation parameters, with different relative risk parameters, or with different numbers of triads per study.
Log-Linear–Modeling Approach
An alternative way to study genotype-exposure interaction by use of data from case-parent triads is to apply likelihood-based methods to analyze conditional genotype distributions (Schaid 1999a; Witte et al. 1999). With these methods, the unit of analysis is a triad rather than an allele transmitted from a heterozygous parent. Consequently, nonindependence of transmissions is not an issue: so long as no triads have members in common (i.e., a single diseased offspring per family), they will be stochastically independent. The other problem facing interaction tests based on transmissions—namely, differential weighting of mating types across exposures—is also overcome by a properly formulated likelihood analysis based on triads. Here we extend the log-linear approach to incorporate genotype-exposure interaction.
Assuming no maternally mediated and no parent-of-origin effects on risk, one can examine genetic effects alone by fitting counts in the 10 (M,P,C) categories to the following log-linear model (Weinberg et al. 1998; Wilcox et al. 1998 [notation modified from the original]):
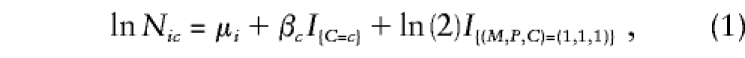 |
where Nic denotes the expected number of triads with C=c and mating type i, where i ranges from 1 to 6 as (M,P) ranges over (2,2), (2,1), (2,0), (1,1), (1,0), and (0,0), respectively. The μi are stratum parameters associated with each mating type; βc=lnRc are logarithms of the relative risk (relative penetrance) parameters associated with C=c, relative to C=0 (so β0=0, by definition); and the indicator function I{relation} takes the value 1 when the relation is true and 0 otherwise. The constant ln2 added in the (M,P,C)=(1,1,1) category, called an “offset” (no parameter is estimated for this term), enforces the Mendelian assumption that two heterozygous parents are twice as likely to produce a heterozygous child as to produce one with either two copies or no copies of the variant allele. Model 1 fits eight parameters, six μi and two βc, to 10 data categories. One could restrict the model to only the informative mating types—(2,1), (1,1), and (1,0)—and get exactly the same inferences (Wilcox et al. 1998), unless some parental genotypes are missing (then, all six mating types are needed [Weinberg 1999a]). On the basis of this model, one can carry out a likelihood-ratio test (LRT) of H0:β1=β2=0 (i.e., no genetic effects), using standard software for log-linear models. This 2-df χ2 test has power that exceeds that of the TDT under either dominant or recessive modes of inheritance (Weinberg et al. 1998; Schaid 1999b) and, like the TDT, is robust against population stratification and admixture. The score test described by Schaid and Sommer (1993) is equivalent to the LRT only in large samples, but results are often close in practice (Weinberg et al. 1998). Estimates and SEs from model 1 are identical to those obtained from a conditional-likelihood approach (Self et al. 1991) or from the condition-on-parental-genotypes approach (Schaid and Sommer 1993) and are readily obtained by use of widely available statistical software.
One can envision fitting model 1 separately to triads with exposed probands and to triads with unexposed probands. A more convenient approach is to formulate a single 16-parameter log-linear model for all 20 (M, P, C, E) categories simultaneously that is equivalent to fitting model 1 separately to each exposure group. Restricting attention to only informative mating types would yield exactly the same inferences, unless some parental genotype data are missing. The encompassing model can be parameterized as
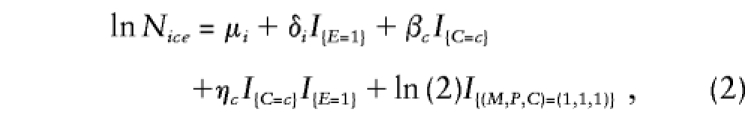 |
where Nice denotes the expected number of triads with (M,P)=i (as described above), C=c, and E=e. Here, the μi are stratum parameters that correspond to the mating-type parameters of model 1 applied to unexposed triads; the μi+δi are the corresponding stratum parameters for exposed triads. The βc are logarithms of the relative risk associated with C=c among the unexposed triads and correspond to the log relative risks that would be estimated by applying model 1 to unexposed triads only; the βc+ηc are the corresponding log relative risks for exposed triads. (Here, β0=η0=0 by definition, since relative risks are compared with risks at C=0.) Consequently, the ηc estimate the two genotype-exposure interaction effects of interest.
To test the no-interaction null hypothesis of interest, H0:η1=η2=0, one calculates a 2-df LRT statistic as twice the difference, in log likelihoods, between model 2 and a reduced version of model 2 in which all ηc are set to 0. This test statistic has approximately a χ2 distribution under the null hypothesis and is equivalent to a test based on a conditional likelihood whose power has been studied by Schaid (1999a).
We have parameterized model 2 under a general genetic-risk model that allows four separate relative risks, depending on the number of copies of the variant allele and on the exposure. Model 2 can easily be tailored to accommodate specific genetic models. For a recessive model, β1 and η1 are eliminated, allowing genetic and interaction effects for two copies of the variant allele only. For a dominant model, replace the four terms for genetic and interaction effects with two terms—namely, βI{C⩾1}+ηI{C⩾1}I{E=1}; for the multiplicative model, in which R2=R21, replace the same four terms, instead, by βC+ηCI{E=1}. For these alternative genetic models, the LRT for interaction has only 1 df and focuses on specific aspects of interaction defined by the genetic model. Model 2 can accommodate triads with one or two missing parents, by adapting the methods of Weinberg (1999a).
The δi parameters are important. By allowing exposed and unexposed triads different sets of stratum parameters through the δi, model 2 properly accommodates the possibility of differential weighting, of mating types, between exposure levels, the problem that we identified earlier as afflicting transmission-based tests of interaction.
Generalizing model 2 from a two-level to a multilevel exposure involves replacing single terms involving I{E=1} with multiple terms involving I{E=e}, for each nonzero exposure level e and introducing additional parameters to accommodate additional exposure levels—namely separate stratum parameters (δie with δi0=0 for each i, by definition) and separate interaction parameters (ηec with η0c=0 for each c and ηe0=0 for each e, by definition).
The log-linear–modeling approach outlined above is flexible and is conveniently implemented with widely available software for Poisson regression (e.g., SAS or GLIM). Moreover, it overcomes the two problems that invalidated the approach based on comparison of transmissions. For example, simulations that use the same data that showed an empirical type I error rate of .474 for the transmission-based χ2 test showed an empirical error rate of .049 (SE .002) when using model 2 to test for interaction.
Limitations on Usefulness
If the assumptions underlying valid statistical analysis of case-parent designs do not hold for the candidate gene under study, results of case-parent analyses, whether via log-linear models or via any other method proposed for case-parent data, can be misleading or biased. We consider those assumptions now.
The Mendelian Assumption
Every method for the analysis of case-parent triad data relies on the fundamental assumption that, for each parental mating type, offspring genotypes in the population follow Mendelian proportions at the ages when probands come under study. With case-parent data, genetic effects are assessed on the basis of whether observed data deviate systematically from what is expected under this Mendelian assumption (Spielman and Ewens 1996). The transmission rate of .5, the TDT's null hypothesis, is derived under the assumption of Mendelian proportions, and the null values of the log-linear model rely on them too. For example, children from mating type (1,1) with 2, 1, or 0 copies of the variant allele are expected to occur in the ratio 1:2:1 in the population at large. These same ratios should occur in case-parent triads when the allele is unrelated to the disease. Observing 50, 100, and 25 triads in mating type (1,1) with 2, 1, and 0 copies of the variant allele, respectively, one would interpret the strong deviation from expected ratios as favoring a genetic effect on disease risk. Model 1 fitted to these data estimates both R1 and R2 as 2. These estimates depend explicitly on the assumed Mendelian ratios in the following sense: if one knew that individuals without the variant allele were half as likely to survive to the age for study as were carriers of that allele, the appropriate ratio would be 2:4:1, and, for that ratio, the data fully support R2=R1=0. Assessing both genetic effects and genotype-exposure interaction requires that this fundamental Mendelian assumption holds separately for offspring genotypes at each exposure level; interaction is inferred when the pattern of deviations from assumed proportions differs between exposure levels.
Deviations from the Mendelian standard can occur (Sherman 1997). Whereas deviations due to asymmetries in gametogenesis, gamete viability, or zygote formation may be rare, those due to differential survival may be more common. For example, certain genotypes may decrease the likelihood of a fetus surviving to birth, distorting away from Mendelian proportions the genotype distribution in living offspring (Tsai et al. 1998). Whenever non-Mendelian transition ratios are the appropriate reference values, tests and estimates based on assumed Mendelian ratios will be biased—whether based on allele transmissions, such as in the case of the TDT, or on genotype distributions within parental mating types.
The Conditional Independence Assumption
Examination of genotype-exposure interactions by use of case-parent data relies on the additional assumption that, conditional on the parents' genotypes, an individual' s exposure status is independent of his or her genotype at the candidate locus. Formally, this conditional independence assumption can be expressed as 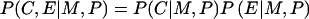 . Appendix A explains mathematically why this assumption is needed.
. Appendix A explains mathematically why this assumption is needed.
One way that conditional independence could fail is if the variant allele itself—or a variant at a linked locus—directly influences a person's propensity for exposure, by affecting that person's appetite or aversion. One example involves alcohol exposure and a variant of the aldehyde dehydrogenase gene, ALDH2, one of several loci involved in the detoxification of alcohol (Enomoto et al. 1991; Shen et al. 1997; Chen et al. 1998). One variant at this locus, ALDH2*2, encodes a protein that converts acetaldehyde to acetate more slowly than do the protein products of other alleles. Carriers of this variant allele tend to avoid alcohol, because a buildup of acetaldehyde after drinking causes discomfort and a flushing reaction.
To see that such situations can distort inferences from case-parent data, consider the artificial data in table 2. These data are expected counts from a population composed of two subpopulations, each in Hardy-Weinberg equilibrium: one, with exposure prevalence and allele frequency each equal to .5, makes up 75% of the population; a second, with exposure prevalence and allele frequency each equal to .2, makes up the remaining 25%. The risk of disease among unexposed individuals without the variant allele who are in the second subpopulation is five times that in the first. In both subpopulations, exposure has no effect on risk itself and R2=R1=1 whether a person is exposed or not. When conditional independence holds, exposure prevalence is .5 and .2 in each subpopulation, respectively. When conditional independence fails, exposure prevalences are .5, .6, or .9 and .2, .4, or .8, as C is 0, 1, or 2, in each subpopulation, respectively. When the conditional independence holds, model 2 correctly finds no evidence of either genetic effects or genotype-exposure interactions (R2=R1=1 at both exposure levels). When the variant allele predisposes carriers to exposure, however, the same analysis wrongly indicates genetic effects within each exposure group (Rc≠1 for c=1 and 2 at either exposure level) and highly significant genotype-exposure interaction (RUc≠REc for c=1 and 2). In this latter case, the variant allele appears to be beneficial among the unexposed but harmful among the exposed. Confronted with such a pattern, an investigator might discount it as biologically problematic or, alternatively, attempt to bolster it by appealing to some hypothetical but plausible mechanism. In general, a pattern in which an allele confers risk among the exposed but reduces risk among the unexposed (or vice versa) should raise the suspicion that the allele under study may influence exposure.
Table 2.
Examples Illustrating Effects of the Conditional Independence Assumption on Estimates and on Fit of Model 2 When Exposure Has No Effect on Risk[Note]
| When ConditionalIndependence Holds |
When Child'sGenotype ModifiesProbability of Exposurea |
|||
| ParentalMating Typeand No. ofCopies ofVariantAllele inOffspring | E = 1 | E = 0 | E = 1 | E = 0 |
| Approximate Expected Count |
||||
| (1,2): | ||||
| 2 | 25 | 30 | 49 | 6 |
| 1 | 25 | 30 | 31 | 24 |
| (1,1): | ||||
| 2 | 15 | 25 | 34 | 6 |
| 1 | 30 | 49 | 41 | 38 |
| 0 | 15 | 25 | 15 | 25 |
| (0,1): | ||||
| 1 | 49 | 126 | 79 | 96 |
| 0 | 49 |
126 |
49 |
126 |
| Estimated R1 |
||||
| 1.00 |
1.00 |
1.55 |
0.76 |
|
| Estimated R2 |
||||
| 1.00 |
1.00 |
2.47 |
0.22 |
|
|
P Value for Test of Genotype-Exposure Interactionb |
||||
| 1.00 |
10−9 |
|||
|
P Value for Test of Fitc |
||||
| 1.00 | .99 | |||
How do biases such as those seen in table 2 arise? Suppose that the variant allele and the exposure have no effect on risk. Then, the Mendelian assumption and the conditional independence assumption together imply that Mendelian transition probabilities hold at each exposure level. Thus, the log-linear analysis, like other comparable likelihood-based analyses, assesses genotypic effects on risk at each exposure level in comparison with the Mendelian proportions. This comparison is appropriate when both key assumptions hold. When the Mendelian assumption holds but conditional independence does not, the comparison is no longer appropriate. Suppose that conditional independence fails so that those individuals in each mating type who have more copies of the variant allele have increased probability of exposure, compared with those with fewer copies. In that situation, exposed probands carrying the variant allele will be overrepresented in each mating type, compared with Mendelian proportions: corresponding unexposed probands will be underrepresented. These distortions in conditional genotype distributions properly reflect the genotype's influence on exposure, but they contradict the Mendelian transition probabilities at each exposure level, leading to the bias seen in table 2. Biases would be in the opposite directions if the variant allele lowered the probability of exposure. The same mechanism would also operate when genetic effects or genotype-exposure interactions did exist, and this would bias inferences in that setting as well.
Exposure Effects
For the study of the joint effects of genotype and exposure on disease risk, case-parent designs can test or estimate genetic effects and genotype-exposure interaction effects, but they cannot evaluate exposure effects. The reason is simple: the data provide no reference values against which to assess how exposure alone may affect disease risk. If one were willing, however, to assume some defensible reference values, then exposure effects could, in principle, be examined with case-parent data, by use of log-linear models. For example, suppose that one viewed sex as a binary “exposure” of interest and was willing to assume a 51:49 male:female sex ratio throughout the population (i.e., in every subpopulation); this effect of sex on disease risk could be studied, provided that all other needed assumptions were satisfied. For this estimation to be valid in stratified populations, the exposure prevalence must be the same in every subpopulation (although allele frequencies may differ). To conduct this analysis, model 2 must be modified by replacement of the original six δi parameters by a single δ parameter, measuring the exposure effect, and inclusion of an additional offset (denoted ω), to become
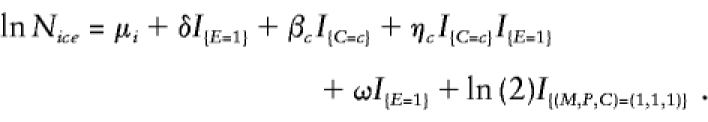 |
Here, ω is set to the natural logarithm of the assumed ratio of exposed to unexposed individuals in the population at large (i.e., the natural logarithm of the odds of exposure). For the example, when males are considered as exposed, ω would be set to ln (51/49).
Detection of Violations of Needed Assumptions
Might the data themselves provide evidence of violated assumptions? Because models 1 and 2 have fewer parameters than (M, P, C) categories, 2- or 4-df (χ2) LRTs of fit can be constructed for models 1 or 2, respectively, by comparing the fitted model with one that has a separate parameter for each data category.
For the moment, ignore exposure. General transition ratios for the informative mating types can be parameterized as indicated in table 3, by use of four values that we denote collectively by vector g=(g1,g2,g3,g4). In particular, gM=(1,1,1,1) corresponds to the Mendelian assumption. Because genetic effects are assessed through certain departures from the Mendelian transition ratios, testing the fit to model 1 can detect only departures that differ from those that the model interprets as genetic effects. Non-Mendelian transition ratios with the form g0=(s/r,s,r,r), where r and s are arbitrary positive constants (table 3), would not register as lack of fit but, rather, as spurious genetic effects, since the mathematical form is exactly that induced by R1 and R2. On the other hand, if g differed in form from g0, then the non-Mendelian ratios might show up as both lack of fit and spurious genetic effects.
Table 3.
General, Nondetectable, and Mendelian Transition Ratios for Informative Mating Types
|
Transition ratioa |
|||
| ParentalMating Typeand Copiesof VariantAllele inOffspring | General | Nondetectableb | Mendelian |
| (1,2): | |||
| 2 | g1 | s/r | 1 |
| 1 | 1 | 1 | 1 |
| (1,1): | |||
| 2 | g2 | s | 1 |
| 1 | 2g3 | 2r | 2 |
| 0 | 1 | 1 | 1 |
| (0,1): | |||
| 1 | g4 | r | 1 |
| 0 | 1 | 1 | 1 |
P(C=c∣M,P)/P(C=c*∣M,P), where c* denotes the fewest copies of the variant allele possible for an offspring from a given parental mating type.
Non-Mendelian transition ratios of this form are not detectable as lack of fit to model 1; s and r are arbitrarily positive constants.
Any deviations from the Mendelian assumption that are caused by differential survival among genotypes may, unfortunately, be close in form to g0. If heterozygote or homozygote carriers of the variant allele exhibit increased or decreased survival relative to homozygotes without the variant allele, then they would likely exhibit similar relative changes regardless of mating type, approximately in accord with g0. Consequently, testing the fit of model 1 will, in practice, likely have little power against deviations from the Mendelian assumption.
Testing the fit to model 2 can detect certain departures from either the Mendelian or the conditional independence assumption. However, these tests suffer the shortcomings already mentioned: for theoretical reasons, some kinds of departures can never be detected; and, for practical reasons, the kinds of departures that seem likely to occur in actual populations are close to the theoretically undetectable forms. If the variant allele increases the probability of exposure, then the effects are likely to be similar across mating types. Even without genetic effects on risk, the resulting distribution of offspring genotypes across mating types may have a form close to g0. When exposed and unexposed groups are studied separately, however, the mating-type–specific offspring distributions in each group will be distorted away from their pooled distribution—but not in a way that registers strongly as lack of fit. The example in table 2 illustrates that even strong departure from conditional independence can be virtually undetectable.
Although the Mendelian assumption is crucial to the testing for genetic effects, it is, interestingly, less crucial to the testing for genotype-exposure interaction. Model 2 can be modified to include parameters for the vector g, by replacing the two genetic effect terms βcI{C=c} by the following four terms: g1I{(M,P,C)=(1,2,2)}+g2I{(M,P,C)=(1,1,2)}+g3I{(M,P,C)=(1,1,1)}+g4I{(M,P,C)=(0,1,1)}. These new parameters relax the Mendelian assumption by estimating the transition ratios fused with genetic effects, so the latter cannot be tested separately. The interaction parameters, however, can still be estimated, and hypotheses involving them can be tested. Moreover, the results for interaction are free of any bias due to non-Mendelian transition ratios, so long as the conditional independence assumption holds and the same vector g applies throughout the population.
Discussion
A strength of the case-parent design is its robustness to hidden genetic population structure in studies that focus on genetic risk. By using the parents, one can minimize errors of inference that arise from genetic population structure, either population stratification or admixture, and that could afflict a case-control study. In addition, parents may be more willing to participate than are randomly selected controls. The principal assumption required for the validity of such analysis is that, for each parental mating type, offspring genotypes follow Mendelian proportions at the ages when probands come under study. Because of the strong belief that this assumption should hold to a close approximation in a variety of circumstances, the method seems to be widely applicable when disease onset is early enough for cases to have living parents.
When exposure comes into consideration, robustness against population structure is no longer guaranteed. We have shown that a correlation between allele frequency and exposure prevalence can produce a difference in transmission rates from heterozygous parents to exposed versus unexposed probands even when genotype-exposure interaction does not exist. Analysis using model 2 successfully overcomes this problem. We have also pointed out that, if a proband's genotype influences his or her probability of exposure, then case-parent data can yield spurious conclusions about genotype-exposure interaction, regardless of the analytic method used. Consequently, whether a particular candidate gene can be safely assumed to have no influence on exposure is something that investigators will have to carefully weigh. On the other hand, when the two key assumptions do hold, exposure effects on risk (although not estimable themselves) will not bias tests or estimates of genetic and interaction effects under either model 1 or model 2.
Our finding that transmission-based tests of interaction are invalid also invalidates many apparently straightforward analyses done to assess differences in genetic risk between subcategories of the population. Questions about possible ethnic or sex differences in genetic risk or about differences in genetic effects among subcategories of disease are questions about gene-by-category interactions. Testing such hypotheses by comparing the transmission rates across groups is not valid, for the same reasons that testing the genotype-exposure interactions that way is not. The ubiquitous problems are that transmissions are not independent in general when both parents are heterozygous and that the equal-transmission-rate null hypothesis differs from the no-interaction null hypothesis. For example, if the population consists of subpopulations in which allele frequency is correlated with the risk of severe disease, then transmission rates can differ between disease subcategories when the effect of the variant allele on disease risk is the same for each disease category. The same thing could occur if the categories were ethnic groups that differed in allele frequency even if each group were in Hardy-Weinberg equilibrium.
Although case-parent designs are often portrayed in terms of parents providing well-matched genetic controls, from another viewpoint, the parents do not explicitly supply “control” information—that is, reference values against which deviations from the null hypothesis are measured. Instead, parents' genotypes provide the ability to stratify triads by mating type. After stratification, reference values are actually provided by the Mendelian assumption. Similarly, Mendelian ratios at each exposure level provide no-interaction reference values. The assumption that genotype does not influence exposure is crucial because, without it, Mendelian ratios would not be appropriate reference values for estimation of genetic effects at each exposure level, even when the Mendelian assumption held overall. Fully relaxing the Mendelian assumption is possible, however: one can still estimate or test genotype-exposure interactions but must forgo any other inferences about exposure-specific genetic effects.
Checking crucial assumptions by use of the data under analysis is a useful goal. Although fully checking the Mendelian assumption requires data beyond those contributed by case-parent triads—perhaps from unaffected siblings (Spielman et al. 1993)—and because the same holds for conditional independence, we had thought that certain egregious departures from assumptions might be detected as lack of fit to the log-linear models. Our analysis suggested that situations so flagrant as to register as statistically significant lack of fit are likely to be rare in practice. Still, routine examination of model fit could provide warnings of some unforeseen problems.
Case-parent designs are useful for the study of genetic and genotype–exposure interaction effects on disease when appropriate methods are used for analysis. Although certain assumptions must be satisfied, we expect that, in a great many circumstances, both the Mendelian assumption and the conditional independence assumption will hold to a close approximation. When hidden population structure is absent, the power and efficiency properties that case-parent designs have for the study of interaction compare favorably with—and can even exceed—those of case-control designs (Schaid 1999a; Witte et al. 1999). When hidden population structure is present, case-parent designs are more robust than case-control designs. Although case-parent designs can yield spurious inferences when the variant allele under study influences exposure, for many kinds of hidden population structure involving exposure and genotype, case-parent designs can provide correct inferences when case-control designs would not. On the other hand, the general inability of case-parent designs to provide any information about the effects of exposure, per se, limits the biological insight that they can provide. Seeing an exposure that was neutral in the absence of the variant allele and deleterious in its presence might suggest a biological mechanism different than that expected if the exposure were beneficial in its absence and neutral in its presence; by precluding the estimation of exposure effects, case-parent designs can never discriminate those two distinct possibilities, whereas case-control designs can.
Analyzing the case-parent triad data via log-linear models provides a useful approach to the study of genetic and genotype-exposure–interaction effects on disease risk. The principal restriction is that disease onset must occur early enough that parents of cases are commonly available for genotyping. The two critical assumptions that we have discussed are likely to be satisfied in many situations. Most important, likelihood-based approaches such as this one overcome difficulties that invalidate transmission-based approaches to the assessment of genotype-exposure interaction.
Acknowledgments
The authors would like to thank Drs. Allen Wilcox and Norman Kaplan for their helpful comments on earlier drafts of this article.
Appendix A : Rationale for the Conditional Independence Assumption
To examine why the conditional independence assumption is required for model 2, we consider first the probabilistic structure of model 1 and then show how taking account of exposure changes that structure. In a random sample of N triads in which the child is affected, one expects to see N×P(M,P,C∣D) triads, where the parental mating type is (M,P) and the child has C copies of the variant allele. Here, P(M,P,C∣D) denotes the conditional probability of a triad with allele counts (M,P,C) given that the offspring is a case. Using Bayes's theorem,
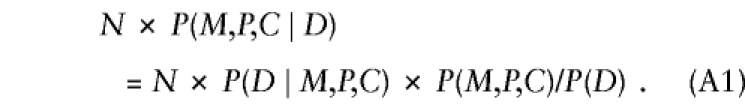 |
In addition to offspring genotype, P(D∣M,P,C) might depend on parental mating type. The latter dependence could arise if the locus under study were in linkage with the actual susceptibility locus, so that the susceptibility allele could be transmitted without simultaneous transmission of the allele under study. Alternatively, if the locus under study is the susceptibility locus itself, then dependence on parental genotype might arise through maternal or imprinting effects. Finally, hidden population structure could induce a dependence of risk on parental mating type. Here, we restrict attention to a susceptibility locus and express 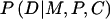 as a product of Rc and a factor that depends on (M,P) alone—that is, P(D∣M,P,C)=RcSMP, where R0=1. This representation embodies the common assumption that the number of copies of the variant allele that a child carries contributes to risk equally regardless of parental mating type. When this assumption is used and P(M,P,C) is reexpressed as P(C∣M,P)×P(M,P), equation (A1) becomes
as a product of Rc and a factor that depends on (M,P) alone—that is, P(D∣M,P,C)=RcSMP, where R0=1. This representation embodies the common assumption that the number of copies of the variant allele that a child carries contributes to risk equally regardless of parental mating type. When this assumption is used and P(M,P,C) is reexpressed as P(C∣M,P)×P(M,P), equation (A1) becomes
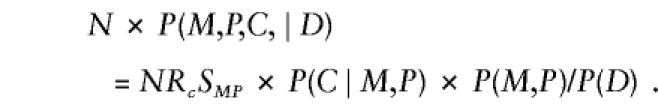 |
Further manipulation yields
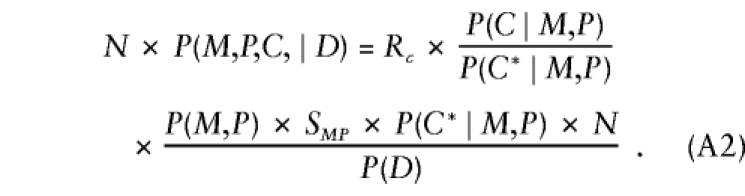 |
Here, C* is the fewest copies of the variant allele that an offspring from a particular parental mating type may have. The first factor on the right-hand side of the equation is the relative risk of disease for a child with C copies of the variant allele, compared with one with no copies; the second factor is the transition ratio from table 3; the third factor is a nuisance parameter that varies only with the mating type in a given study and is accommodated via mating-type–specific stratum parameters. Taking logarithms of both sides of equation (A2) and specifying the log transition ratios as known offsets yields model 1.
Consider next what happens when exposure is included. What we will argue is that to achieve a form analogous to equation (A2) requires an assumption that the child's genotype and exposure are conditionally independent given parental mating type. With exposure included, the analogue of equation (A1) is
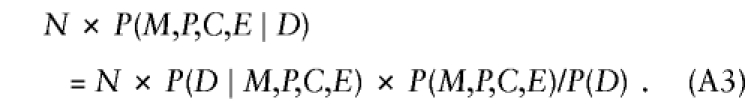 |
Besides child's genotype and exposure, P(D∣M,P,C,E) might depend on parental mating type, through the same mechanisms mentioned earlier, when exposure was ignored. Here we generalize to more than two levels of exposure, by allowing E to take values 0, 1, 2, ..., k indicating exposure level. Again, we restrict attention to a susceptibility locus and express P(D∣M,P,C,E) as a product of (i) REc, the relative risk associated with C copies of the variant allele relative to no copies at exposure level E, and (ii) a factor that depends on (M,P) and E—namely, P(D∣M,P,C,E)=REc×SMPE, where RE0=1 for all values of E. In addition, one can express P(M,P,C,E) formally as
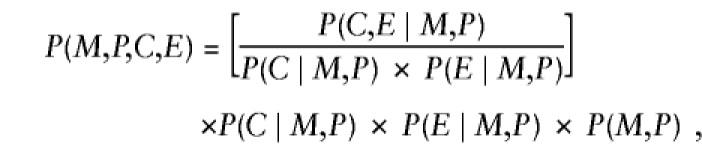 |
where the factor in square brackets—say, ΔEC∣MP—measures the departures from stochastic independence of E and C, given parental mating type (ΔEC∣MP=1 when conditional independence holds). After substitution of these results, further manipulation reexpresses equation (A3) as
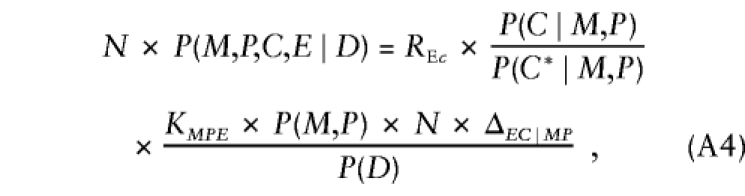 |
where KMPE=SMPE×P(E∣M,P)×P(C*∣M,P). In this representation, the first factor gives the relative risk; the second factor is again the transition ratio; and, aside from ΔEC∣MP, the third factor is a nuisance parameter that depends on parental mating type and exposure alone and is handled through stratum parameters that are specific to combinations of exposure level and parental mating type. Thus, when ΔEC∣MP=1, taking the logarithms of both sides of equation (A4) and specifying the log transition ratios as known offsets yields model 2. When ΔEC∣MP≠1, model 2 cannot correctly represent the probabilistic structure given by equation (A4) and is not valid for analysis of triad data. If the analyst could specify appropriate values of ΔEC∣MP (or some equivalent measure of departure from independence), then model 2 could be modified with appropriate offsets to be valid under that particular conditional dependence relationship. Situations in which ΔEC∣MP could be specified a priori are probably rare.
References
- Chen WJ, Chen C-C, Yu J-M, Cheng ATA (1998) Self-reported flushing and genotypes of ALDH2,ADH2, and ADH3 among Taiwanese Han. Alcohol Clin Exp Res 22:1048–1052 [PubMed]
- Enomoto N, Takase S, Yasuhara M, Takada A (1991) Acetaldehyde metabolism in different aldehyde dehydrogenase-2 genotypes. Alcohol Clin Exp Res 15:141–144 [DOI] [PubMed]
- Flanders WD, Khoury MJ (1996) Analysis of case-parental control studies: method for the study of associations between disease and genetic markers. Am J Epidemiol 144:696–703 [DOI] [PubMed]
- Greenland S, Rothman KJ (1998) Concepts of interaction. In: Rothman KJ, Greenland S (eds) Modern epidemiology, 2d ed. Lippincott-Raven, Philadelphia, pp 329–342 [Google Scholar]
- Harley JB, Moser KL, Neas BR (1995) Logistic transmission modeling of simulated data. Genet Epidemiol 12:607–612 [DOI] [PubMed]
- Khoury MJ (1994) Case-parental control method in the search for disease-susceptibility genes. Am J Hum Genet 55:414–415 [PMC free article] [PubMed]
- Khoury MJ, Flanders WD (1996) Nontraditional epidemiologic approaches in the analysis of gene-environment interaction: case-control studies with no controls. Am J Epidemiol 144:207–213 [DOI] [PubMed]
- Maestri NE, Beaty TH, Hetmanski J, Smith EA, McIntosh I, Wyszynski DF, Liang K-Y, et al (1997) Application of transmission disequilibrium tests to nonsyndromic oral clefts: including candidate genes and environmental exposures in the models. Am J Med Genet 73:337–344 [DOI] [PubMed]
- Schaid DJ (1999a) Case-parents design for gene-environment interaction. Genet Epidemiol 16:261–273 [DOI] [PubMed]
- ——— (1999b) Likelihoods and TDT for the case-parents design. Genet Epidemiol 16:250—260 [DOI] [PubMed]
- Schaid DJ, Sommer SS (1993) Genotype relative risks: methods for design and analysis of candidate-gene association studies. Am J Hum Genet 53:1114–1126 [PMC free article] [PubMed]
- Self SG, Longton G, Kopecky KJ, Liang K-Y (1991) On estimating HLA/disease association with application to a study of aplastic anemia. Biometrics 47:53–61 [PubMed]
- Shen Y-C, Fan J-H, Edenberg HJ, Li T-K, Cui Y-H, Wang Y-F, Tian C-H, et al (1997) Polymorphism of ADH and ALDH genes among four ethnic groups in China and effects upon the risk for alcoholism. Alcohol Clin Exp Res 21:1272–1277 [PubMed]
- Sherman SL (1997) Evolving methods in genetic epidemiology. IV. Approaches to non-Mendelian inheritance. Epidemiol Rev 19:44–51 [DOI] [PubMed]
- Spielman RS, Ewens WJ (1996) The TDT and other family-based tests for linkage disequilibrium and association. Am J Hum Genet 59:983–989 [PMC free article] [PubMed]
- Spielman RS, McGinnis RE, Ewens WJ (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed]
- Tsai AF, Kaufman KA, Walker MA, Karrison TG, Odem RR, Barnes RB, Scott JR, et al (1998) Transmission disequilibrium of maternally-inherited CTLA-4 microsatellite alleles in idiopathic recurrent miscarriage. J Reprod Immunol 40:147–157 [DOI] [PubMed]
- Weinberg CR (1999a) Allowing for missing parents in genetic studies of case-parent triads. Am J Hum Genet 64:1186–1193 [DOI] [PMC free article] [PubMed] [Google Scholar]
- ——— (1999b) Methods of detecting parent-of-origin effects in genetic studies of case-parents triads. Am J Hum Genet 65:229–235 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberg CR, Wilcox AJ, Lie RT (1998) A log-linear approach to case-parent-triad data: assessing effects of disease genes that act either directly or through maternal effects and that may be subject to parental imprinting. Am J Hum Genet 62:969–978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilcox AJ, Weinberg CR, Lie RT (1998) Distinguishing the effects of maternal and offspring genes through studies of “case-parent triads.” Am J Epidemiol 148:893–901 [DOI] [PubMed]
- Witte JS, Gauderman WJ, Thomas DC (1999) Asymptotic bias and efficiency in case-control studies of candidate genes and gene-environment interactions: basic family designs. Am J Epidemiol 149:693–705 [DOI] [PubMed]


