Summary
High-resolution mapping is an important step in the identification of complex disease genes. In outbred populations, linkage disequilibrium is expected to operate over short distances and could provide a powerful fine-mapping tool. Here we build on recently developed methods for linkage-disequilibrium mapping of quantitative traits to construct a general approach that can accommodate nuclear families of any size, with or without parental information. Variance components are used to construct a test that utilizes information from all available offspring but that is not biased in the presence of linkage or familiality. A permutation test is described for situations in which maximum-likelihood estimates of the variance components are biased. Simulation studies are used to investigate power and error rates of this approach and to highlight situations in which violations of multivariate normality assumptions warrant the permutation test. The relationship between power and the level of linkage disequilibrium for this test suggests that the method is well suited to the analysis of dense maps. The relationship between power and family structure is investigated, and these results are applicable to study design in complex disease, especially for late-onset conditions for which parents are usually not available. When parental genotypes are available, power does not depend greatly on the number of offspring in each family. Power decreases when parental genotypes are not available, but the loss in power is negligible when four or more offspring per family are genotyped. Finally, it is shown that, when siblings are available, the total number of genotypes required in order to achieve comparable power is smaller if parents are not genotyped.
Introduction
Increasingly large numbers of single-nucleotide polymorphisms are available in public and private databases (Collins et al. 1997). The emergence of high-throughput methods for their analysis holds promise for saturation mapping of human complex-disease loci (Risch and Merikangas 1996; Chakravarti 1998; Lander 1999). Whereas allele-sharing methods of linkage analysis can localize disease genes to broad chromosomal regions, in complex diseases their resolution is often poor. Accordingly, the effort spent in generating an increasingly fine map provides rapidly diminishing returns when these conventional methods of linkage analysis are used (Kruglyak 1997).
In outbred samples, allelic association due to linkage disequilibrium is expected to operate over very short distances. Appropriately designed tests of association that use family-based controls to account for population substructure can provide direct tests of linkage disequilibrium and efficient fine-mapping tools. These tests should have much greater power when a fine map is available, and their high resolution should be well suited to identification of candidate genes.
The most popular of these family-based tests of association is the transmission/disequilibrium test (TDT), which was introduced by Spielman et al. (1993) as a test of linkage in the presence of allelic association. When either a single affected child is tested in each family or, with appropriate adjustments (Martin et al. 1997), multiple children are tested, it is often used as a test of linkage disequilibrium (i.e., a test of the joint hypothesis of linkage and association). The TDT was designed for the analysis of dichotomous traits, and a number of refinements have been proposed to allow, for example, the use of siblings as controls (Curtis 1997) and increased power in the presence of imprinting or dominance (Weinberg et al. 1998).
It has been shown that tests of transmission disequilibrium require a larger number of families in order to achieve comparable power when siblings, rather than parents, are used to construct controls (Curtis 1997). However, it is not always practical to collect parents, and attempting to deduce parental genotypes is fraught with pitfalls (Curtis and Sham 1995). Ideally, TDT-like tests should use parental genotypes when available and sibling genotypes otherwise, to consider all available information in the most efficient manner possible.
For many complex diseases, quantitative phenotype scores contain more information than is provided by dichotomous traits. Quantitative traits can provide effective descriptions of conditions as varied as asthma, type II diabetes, learning difficulties, and osteoporosis. The use of quantitative traits is well established in linkage studies, and these traits should be equally effective in family-based tests of association. Allison (1997) and Rabinowitz (1997) introduced family-based linkage tests, for quantitative traits; like the TDT, these tests use parental genotypes to construct well-matched controls and that are tests of linkage disequilibrium in simplex families. Fulker et al. (1999) described an analogous test for sib-pair data that does not use parental genotypes.
Here we present a general linkage-disequilibrium test that is applicable to the analysis of quantitative traits in nuclear families of any size and that optionally uses parental genotypes. The method builds on the recent approach of Fulker et al. (1999), in that association effects are partitioned into between- and within-family components. The model also makes use of the powerful and flexible variance-components framework, to construct tests of linkage, linkage disequilibrium, and population admixture that use information from all available offspring. In addition to extending this model to accommodate nuclear families of any size, we derive the expectations of the model parameters and show that a test of the within-family component is indeed free of confounding population-substructure effects, regardless of the composition of nuclear families. We also show that admixture impacts the between-family–component estimate when samples from a number of population strata are combined. This general model encompasses the specific test and study design of Fulker et al. (1999), as well as that of Rabinowitz (1997). The properties of the model in terms of power and error rates are explored in a number of situations, including moderate sample sizes and violation of the multivariate normality assumption underlying variance-components methods. Power and optimal study designs in terms of parental information and family size are also examined.
Maximum-Likelihood Tests of Association
Consider a candidate diallelic marker, M, with alleles arbitrarily designated as “1” (with frequency p) and “2” (with frequency q=1-p) and an additive genetic value a. Note that our usage of the additive genetic value refers to the observed marker, not the trait locus, and that a≠0 only when the marker locus is either the trait locus or in disequilibrium with it. Also, as long as the phase of the association is the same in all subpopulations, a=0 only when there is no linkage disequilibrium. Given a set of i=1…K nuclear families, each with ni children so that the total number of offspring is N=Σini, define the marker phenotype mij and the genotype score gij for the jth offspring (j=1…ni) in the ith family as mij=number of “1” alleles at locus M, and gij=mij-1. If both parental genotypes are known, label their analogous genotype scores giM and giF for the male and female parent, respectively.
Following the usual biometric model (Falconer 1989), we assume that the phenotype scores for the trait of interest are defined by a major-gene effect, familial effects (which include the effects of shared environment and half the additive polygenic variance), and a residual environmental component. The expected mean of the residual resemblance and unique environmental effects are assumed to be 0, so that
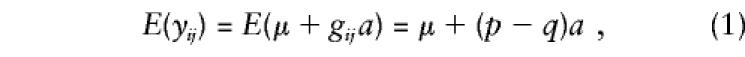 |
and, for the offspring in each family, the ni×ni variance-covariance matrix, Ωi, has elements
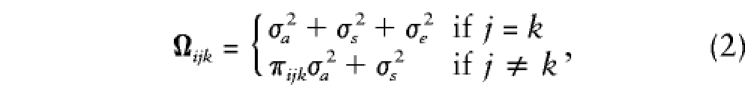 |
where πijk denotes the proportion of alleles shared identical by descent (IBD) between siblings j and k in family i, σ2a is the additive genetic variance of the major gene, σ2s is the residual sibling resemblance, and σ2e is the residual environmental variance component. Note that these expectations do not include any dominance variance, although the general method can easily accommodate such effects (Fulker et al. 1999; also discussed below).
Variance-components approaches allow simultaneous modeling of the means and variances, so that all the information in a set of related individuals can be used to construct a test of association. For a particular means model, such as
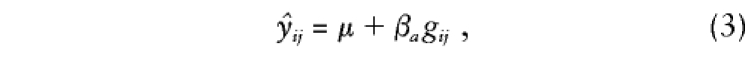 |
and for estimates of all of the variances in Ωi, the likelihood of the data for the complete set of parameters, θ=[μ,βa,σ2a,σ2s,σ2e], is
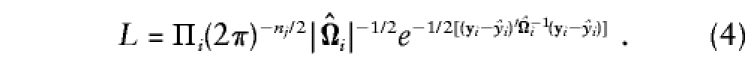 |
Evidence for association can be evaluated by maximization of L with the constraint βa=0 (null-hypothesis likelihood, L0) and without constraints on the parameters (alternative-hypothesis likelihood, L1). Asymptotically, the quantity 2[ln(L1)-ln(L0)] is distributed as χ2, with df equal to the difference in number of parameters estimated. Similar likelihood-ratio tests have been proposed as tests of association between marker and phenotype (e.g., see George and Elston 1987), and, in the absence of population admixture, they are valid tests of linkage disequilibrium, because E(βa)=a. For families with exactly two siblings, this model is the same as the general model of Fulker et al. (1999).
Population Admixture
We allow for the most extreme form of population admixture, in which each family is drawn from a different stratum. Define μi, pi, and qi, the phenotypic mean and allele frequencies for the stratum from which family i was drawn. Assume that within each subpopulation there is random mating and random transmission of parental alleles to offspring and that the total sample of N individuals is centered on mean 0; that is, μ=Σiniμi=0.
In this situation, the expectation given in equation (1) can be expressed as E(yij)=E(μi+gija)=μi+(pi-qi)a, and the alternative hypothesis of no linkage disequilibrium is no longer encompassed in a test of βa≠0. As shown in Appendix A, in this case, E(βa)=Σini(pi-qi)μi/(NVg)+a, where Vg is the variance of the genotypic scores. The numerator of the first term in this expression represents “spurious” association, at the population level, that is independent of linkage.
Orthogonal Decomposition of the Genotype Scores
Fulker et al. (1999) proposed that, for sib-pair data, the genotype score could be decomposed into orthogonal between-family (b) and within-family (w) components, in which only the former is sensitive to population structure and in which the latter is significant only in the presence of linkage disequilibrium. The means model under this specification is
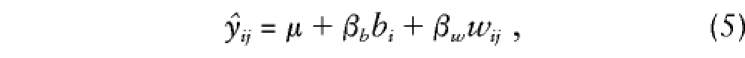 |
where bi and wij are orthogonal between- and within-family components of gij. We extend this model to accommodate any number of offspring, with or without parental genotypes, as
 |
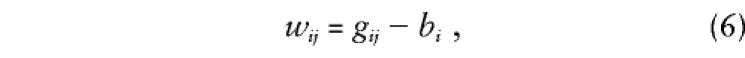 |
so
that bi is the expectation of each
gij conditional on family data and
wij is the deviation from
this expectation for offspring j. Note that, when
bi=(Σjgij)/ni,
all possible siblings are considered and parental data are ignored,
whereas, when
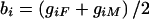 ,
only parental data are used (for an example of how
bi and
wij are scored, with and without
parental data, see table 1).
Positive values of wij indicate that
a child inherits more copies of allele “1” than would be
expected, whereas negative values refer to inheritance of an excess of
allele “2.” For sib-pair data for which parental
genotypes are not available, which is the situation described by Fulker et
al. (1999),
wi1=-wi2 for any
i, so that different alleles are tested in each member of a
sib pair and the distribution of βw is
unaffected by linkage in the absence of association.
,
only parental data are used (for an example of how
bi and
wij are scored, with and without
parental data, see table 1).
Positive values of wij indicate that
a child inherits more copies of allele “1” than would be
expected, whereas negative values refer to inheritance of an excess of
allele “2.” For sib-pair data for which parental
genotypes are not available, which is the situation described by Fulker et
al. (1999),
wi1=-wi2 for any
i, so that different alleles are tested in each member of a
sib pair and the distribution of βw is
unaffected by linkage in the absence of association.
Table 1.
Example Scoring of bi and wij in a Sib Pair[Note]
| Offspring | Parental Information | Sibs only | ||||||
| gi1 | gi2 | P(g) | bi | wi1 | wi2 | bi | wi1 | wi2 |
| One Heterozygous Parent (giF, giM) = (1, 0) | ||||||||
| 0 | 0 | p3q | 1/2 | − 1/2 | − 1/2 | 0 | 0 | 0 |
| 0 | 1 | 2p3q | 1/2 | − 1/2 | 1/2 | 1/2 | − 1/2 | 1/2 |
| 1 | 1 | p3q | 1/2 | 1/2 | 1/2 | 1 | 0 | 0 |
| Two Parents Heterozygous (giF, giM) = (0, 0) | ||||||||
| −1 | −1 | 1/4p2q2 | 0 | −1 | −1 | −1 | 0 | 0 |
| 1 | 1 | 1/4p2q2 | 0 | 1 | 1 | 1 | 0 | 0 |
| 0 | 0 | p2q2 | 0 | 0 | 0 | 0 | 0 | 0 |
| −1 | 0 | p2q2 | 0 | −1 | 0 | − 1/2 | − 1/2 | 1/2 |
| 0 | 1 | p2q2 | 0 | 0 | 1 | 1/2 | − 1/2 | 1/2 |
| −1 | 1 | 1/2p2q2 | 0 | −1 | 1 | 0 | −1 | 1 |
Note.— For the unordered pairs of parental genotype scores (giF, giM)=(1, 0) and (giF, giM)=(0, 0), the table lists possible offspring genotype scores, and their frequency at the population level. The scoring of bi and wij is illustrated for these cases by use of either parental genotypes or sibling genotypes only. Note that the frequency of these mating types is 4p3q and 4p2q2, respectively.
Fulker et al. (1999) suggested that the βw regression coefficient, when estimated in the context of a variance-components model and in the absence of population admixture, provides a direct estimate of the additive genetic value a. Allowing for population admixture and extending the model to allow both for sibships of any size and for the inclusion of parental genotype data, we derive the expectation of βb and βw for each of these two alternative definitions and show that all the “spurious” association between genotype score and phenotype is accounted for by βb and that the βw regression coefficient remains a direct estimate of the additive genetic value a (at the marker).
By use of the normal equations, equation
(5) can be expressed as
y=Xb+e,
so that
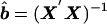 Xy, where X is the design matrix and
Xy, where X is the design matrix and
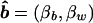 .
X′X and Xy are asymptotically the covariance
matrices between the independent and dependent variables, respectively. To
solve these equations, only the expectations for the
variances, Vb and
Vw, and covariances,
Cb,y and
Cw,y, are required, since
bi and
wij are orthogonal by design. These
quantities are derived in Appendices B and
C.
.
X′X and Xy are asymptotically the covariance
matrices between the independent and dependent variables, respectively. To
solve these equations, only the expectations for the
variances, Vb and
Vw, and covariances,
Cb,y and
Cw,y, are required, since
bi and
wij are orthogonal by design. These
quantities are derived in Appendices B and
C.
Parental Genotypes Available
As shown in Appendix B,
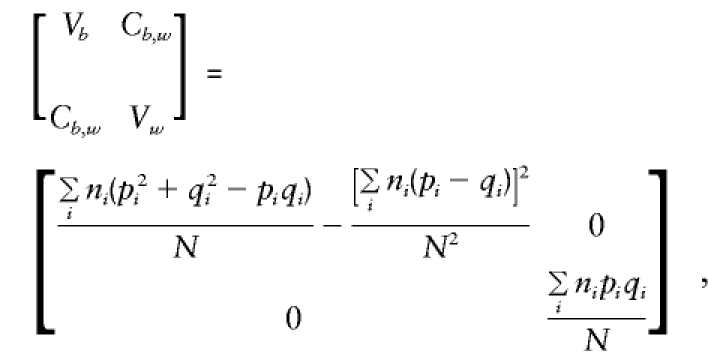 |
and
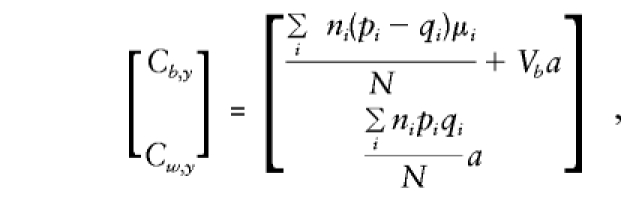 |
so that
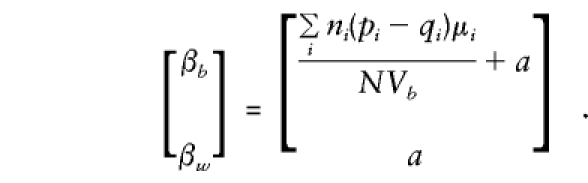 |
Note that all the population-substructure effects in the means, μi, that are apparent in the general specification of E(βa) are included in the expectation of βb exclusively. Whereas βb provides a direct estimate of a only if there is no “spurious” association between g and y (e.g., when all μi are 0 or, since Σiniμi=0, when p and q are constant), βw is independent of any “spurious” effects and remains a valid estimate of a even when there is admixture.
Parental Genotypes Unobserved or Unused
As shown in Appendix C,
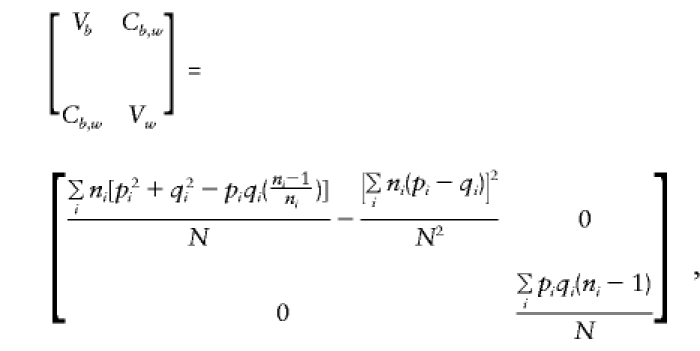 |
and
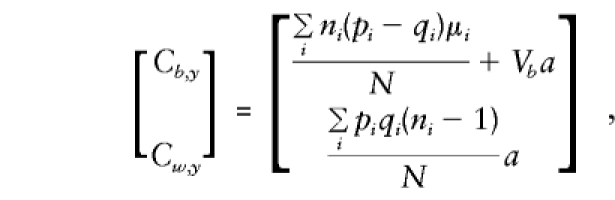 |
so
that, as
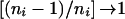 ,
the contribution of each family to
Vb,
Vw,
Cb,y, and
Cw,y approximates that of the case
in which parents are available (given in the previous section). On solution
of the normal
equations,
,
the contribution of each family to
Vb,
Vw,
Cb,y, and
Cw,y approximates that of the case
in which parents are available (given in the previous section). On solution
of the normal
equations,
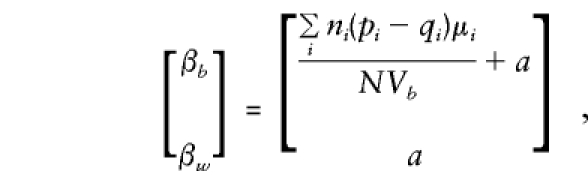 |
so that βw remains a direct estimate of a, independent of population admixture and the number of offspring observed in each family. In contrast, βb is again a direct estimate of a only when there is no “spurious” association between genotype scores, g, and phenotype, y. These expectations show that the admixture test of βb=βw proposed by Fulker et al. (1999) is valid even when parental genotypes are included in analysis and when sibships of size >2 are evaluated.
Simulations
A number of simulation studies were conducted to explore the properties of this orthogonal decomposition of genotype scores as a test of linkage disequilibrium. Data were simulated in nuclear families each having one to eight offspring. Trait values were constructed as the sum of a major-gene effect (with variance σ2a) generated by an additive quantitative-trait locus (QTL), Q, having two equifrequent alleles, a residual sibling correlation (σ2s), and an environmental effect (σ2e), each assigned independently from a normal distribution with mean 0. Except where noted, a diallelic marker locus M, with allele frequencies p=q= 1/2, was simulated with a recombination fraction (θ) of 0. For convenience, the total trait variance σ2=σ2a+σ2s+σ2e was fixed at 100 in all simulations.
Linkage disequilibrium between the trait and marker locus was introduced in the parental chromosomes. When appropriate, disequilibrium was modeled in the usual fashion as D=pM1Q1-pM1pQ1 (pM1Q1 is the frequency of the haplotype with alleles M1 and Q1, and pM1 and pQ1 are the frequencies of alleles M1 and Q1; Lewontin and Kojima 1960), so that Dmax=min(pM1,pQ1)-pM1pQ1, and the standardized disequilibrium coefficient is D/Dmax.
Where noted, population admixture was generated by the mixing of
families drawn from one of two populations (A and B) with different
phenotypic means (μA and μB) and marker
allele frequencies (pA=.7 and
pB=.3) in equal sampling
proportions. μA and μB were selected such
that admixture accounted for 20% of the total phenotypic variance in the
combined population; that is,
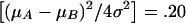
Except where noted, parental genotypes were used to estimate π by use of information available from the single-marker locus (Haseman and Elston 1972). By use of the variance-components model (eq. [2]) and the orthogonal model for the means (eq. [5]), the likelihood was maximized under the null (βw=0) and alternative hypotheses, to calculate L0 and L1, respectively (eq. [4]). As suggested by Searle et al. (1992), the variance-component estimates were constrained to be positive. To examine the benefits of parental information, each simulated data set was examined under the two alternative definitions of bi and wij (see eq. [6]). Only families having at least one heterozygous parent (when parental genotypes were used) or at least two different types of offspring (when parental genotypes were ignored) were included in the likelihood calculations, since other families do not contribute to estimates of βw. For the purpose of our simulations, power and error rates were defined as the proportion of simulations exceeding nominal significance levels for the χ2 distribution under the likelihood-ratio criteria.
It is well known that segregation of a major locus violates the multivariate normality assumption and that maximum-likelihood estimates of the variance components can be biased in small samples (Amos et al. 1996). To characterize the effect that that bias has on the present test, error rates of βw were examined for a range of sample sizes (i.e., 120–1,920 offspring) and family structures (1–8 children), in the following situations: (1) no sibling correlation or major-gene effect (σ2s=σ2a=0) in homogeneous and admixed populations, (2) a large major-gene effect (σ2a=30) or a large residual sibling correlation (σ2s=50), and (3) both residual sibling correlation and major-gene effect (σ2a=20, σ2s=30). Five thousand simulated data sets were examined in each test case. No disequilibrium was modeled in any of these simulations.
The effects that family structure and linkage disequilibrium have on power were examined in a sample of 480 total offspring when σ2a=10 and σ2s=30, by varying D between 0 and Dmax and varying, from one to eight, the number of offspring in each family. In these assessments, the total number of offspring sampled was fixed, so that the number of families varied according to sibship size. Finally, the sensitivity of the test to linkage disequilibrium was estimated for a variety of sample sizes and family structures. Sensitivity was defined as the most stringent significance level that could be obtained with 80% power in simulated data sets in which the trait and marker loci were identical. When power and test sensitivity were examined, 1,000 simulated data sets were analyzed in each case.
Permutation Test
For each family, the vector wi denotes the observed pattern of allelic transmission. In the absence of linkage disequilibrium, the vectors wi and −wi are equally likely, as long as there is no segregation distortion. Construct a random permutation of any set of K families by replacing each wi with either itself or −wi, with equal probability, so that, for any given data set, there are 2K different permutations of the data. The distribution of the maximum likelihood of the data, L1, under the hypothesis of no linkage disequilibrium is the distribution of the maximum likelihoods of these 2K permuted data sets. When the distribution of 2[ln(L1)-ln(L0)] is not well approximated by the χ2 distribution, the distribution of L1 can be estimated by a sampling of a large number of permutations and their respective likelihoods. These empirical P values and the likelihood-ratio criterion were compared in a small sample (120 total offspring) in which the major-gene effect was introduced by simulation of a dominant QTL with equally frequent alleles. In this situation, empirical significance levels should be desirable because both dominance (which both induces nonnormality into the trait distribution and makes the variances model [eq. {2}] incomplete) and the small sample size are expected to reduce the accuracy of asymptotic significance levels. For dichotomous traits, the increased error rates of likelihood-ratio tests in small samples, as well as their spurious effect on power, have been described by Whittaker and Thompson (1999). The rationale for permutation tests in linkage studies has been discussed by Wan et al. (1997).
Type 1–Error Rates
Error rates in estimates of the βw parameter in various test cases are presented in tables 2 and 3. Additional family structures were examined, but the results were intermediate between those tabulated and are not shown. A large major gene and sibling resemblance were selected for description of error rates, to make any possible biases obvious. When one child from each family was considered, error rates were not influenced by population admixture or by the effects of the linked major locus or additional sibling resemblance, so that only a summary error rate over all test cases is reported.
Table 2.
Error Rates When Parents Are Available
|
Error
Rateb When
Total No. of Offspring
Is |
|||||
| Offspring per Family and Test Casea | 120 | 240 | 480 | 960 | 1,920 |
| 1: | |||||
| Overall | 5.5 | 5.3 | 5.4 | 5.1 | 5.1 |
| 2: | |||||
| Null | 5.4 | 5.0 | 5.3 | 4.8 | 5.0 |
| Admixture | 5.6 | 5.4 | 5.4 | 4.6 | 5.7 |
| Sibling resemblance | 4.8 | 5.0 | 4.7 | 4.4 | 5.2 |
| Linkage | 7.0 | 5.4 | 5.7 | 5.0 | 5.3 |
| Composite | 5.6 | 4.8 | 4.9 | 5.4 | 5.1 |
| 4: | |||||
| Null | 5.1 | 5.1 | 4.9 | 4.5 | 4.2 |
| Admixture | 5.0 | 4.9 | 4.5 | 5.2 | 4.7 |
| Sibling resemblance | 4.8 | 5.0 | 4.7 | 4.4 | 4.8 |
| Linkage | 7.0 | 5.4 | 5.7 | 5.0 | 5.2 |
| Composite | 5.6 | 4.8 | 4.9 | 5.4 | 5.3 |
| 8: | |||||
| Null | 4.9 | 5.3 | 5.7 | 4.8 | 5.5 |
| Admixture | 4.5 | 4.4 | 4.9 | 4.2 | 5.2 |
| Sibling resemblance | 4.4 | 4.0 | 4.5 | 4.7 | 4.8 |
| Linkage | 6.5 | 6.2 | 5.9 | 5.8 | 6.1 |
| Composite | 5.2 | 5.3 | 5.0 | 5.2 | 4.7 |
Null = no sibling resemblance, or major-gene effect (s2=h2=0); Admixture = no sibling resemblance, or major-gene effect (s2=h2=0, with population admixture); Sibling resemblance = large sibling resemblance (s2=.5); Linkage = linked major gene of large effect (h2=.3, θ=0); Composite = composite test case (s2=.3 and h2=.2, θ=0). There was no linkage disequilibrium between QTL and marker locus (D=0). For single-child families, only the overall error rate is reported. Each estimate is based on 5,000 replicates.
Shown as the proportion of simulations exceeding the nominal significance level, .05.
Table 3.
Error Rates When Parents Are Unavailable or Unused[Note]
|
Error
Rateb When
Total No. of
Offspring Is |
|||||
| Offspring per Familyand Test Casea | 120 | 240 | 480 | 960 | 1,920 |
| 2: | |||||
| Null | 6.5 | 6.1 | 5.7 | 5.3 | 5.1 |
| Admixture | 6.6 | 6.0 | 4.6 | 4.2 | 4.8 |
| Sibling resemblance | 5.4 | 5.5 | 5.5 | 4.7 | 5.1 |
| Linkage | 7.1 | 5.7 | 6.0 | 5.7 | 5.3 |
| Composite | 5.7 | 5.2 | 5.2 | 5.2 | 4.9 |
| 4: | |||||
| Null | 5.3 | 5.4 | 4.5 | 4.6 | 4.8 |
| Admixture | 5.1 | 4.1 | 4.4 | 4.7 | 4.6 |
| Sibling resemblance | 4.3 | 4.4 | 4.6 | 4.6 | 4.7 |
| Linkage | 6.2 | 6.1 | 5.7 | 5.7 | 5.3 |
| Composite | 5.5 | 6.1 | 5.5 | 5.2 | 4.8 |
| 8: | |||||
| Null | 5.2 | 4.9 | 5.4 | 4.8 | 5.2 |
| Admixture | 4.2 | 4.2 | 4.6 | 4.2 | 5.0 |
| Sibling resemblance | 3.5 | 4.3 | 4.8 | 3.9 | 4.8 |
| Linkage | 7.7 | 6.9 | 5.9 | 5.6 | 5.5 |
| Composite | 6.1 | 5.7 | 5.2 | 5.2 | 5.4 |
Note.— The simulated data sets are the same as those used in table 1, but parental genotypes were not considered during the analysis.
Test cases are as defined in table 2.
Shown as the proportion of simulations exceeding the nominal significance level, .05.
The error rates for the rows labeled “Null” in tables 2 and 3 should be considered as baseline error rates for the other test cases. Not surprisingly, error rates were closer to nominal significance levels in larger samples, where the likelihood-ratio criterion is more accurate. For very large samples, the asymptotic criteria seem to be appropriate regardless of model or sibship size (tables 2 and 3). In smaller samples, error rates are slightly high for the linkage test case and are slightly low for the admixture and sibling-resemblance test cases, an effect that is more pronounced for larger sibships. When only a small number of observations are considered, estimates of the variance components may be biased (see Hopper and Mathews 1982; Amos et al. 1996), so that these error rates are not a specific feature of the present model but may reflect violations of multivariate normality.
As the sample size increases, bias in the maximum-likelihood estimates of variance components should be reduced, and the error rate of asymptotic significance tests should approach its nominal level (Amos et al. 1996). These small-sample biases decrease for more-realistic values of σ2a and σ2s. It is interesting to note that, although some bias remains when the variance components are estimated by maximum likelihood, these biases are much larger if only σ2e is considered: for example, if the linkage information is ignored and a traditional least-squares regression framework is adopted, modeling only σ2e and the association parameters, the error rates exceed 11% at the nominal .05 significance level, for all sample sizes examined in the eight-sib linkage-test case in tables 2 and 3.
When parental genotypes are not available for analysis (table 3), it may appear counterintuitive that, although the biases follow the general trends described above, they appear to be greater in the two-sib case. The reason for this increased bias is that wi is not 0 (and therefore informative) in only a small proportion of sib pairs when parental genotypes are not available for analysis, so that the effective sample size is much less than that actually genotyped.
Power Estimates
Results of the power calculations are presented in table 4 and figure 1. When parental genotypes are available, power depends mostly on the amount of disequilibrium between the trait and marker loci and is largely independent of the number of offspring in each family (table 4). In contrast, when parental genotypes are not available, power depends both on family size and on the level of disequilibrium: larger sibships allow a greater proportion of segregating alleles to be identified (and scored to be not 0 in the respective wij), and, thus, power increases with the number of siblings in each family. As might be expected, for any family size, power is always greater when parental genotypes are available for analysis, since all pairs of segregating alleles are evident in this situation. However, for larger sibships (four or more offspring), it appears that ⩽5% power is lost when parental genotypes are unavailable.
Table 4.
Effects of Family Structure and Linkage Disequilibrium on Power[Note]
| D/Dmaxa (%) | One Sib per Family | Two Sibsper Family | Three Sibs per Family | Four Sibsper Family | Five Sibs per Family | Six Sibsper Family | Eight Sibs per Family | 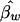 |
| No.
of Families When Total No. of Sibs Is
480 |
||||||||
| 480 |
240 |
160 |
120 |
96 |
80 |
60 |
||
| Power
When Parental Genotypes Are Included in Analysis, for
E(Nw) =
360b |
||||||||
| 0 | .2 | .0 | .1 | .1 | .2 | .1 | .0 | .01 |
| 25 | 2.1 | 1.8 | 2.0 | 2.6 | 3.0 | 2.1 | 2.1 | 1.11 |
| 50 | 19.5 | 22.9 | 24.8 | 26.7 | 26.7 | 27.2 | 23.9 | 2.24 |
| 75 | 69.3 | 72.6 | 74.2 | 76.9 | 76.0 | 76.5 | 75.4 | 3.35 |
| 100 | 97.4 |
97.7 |
98.3 |
98.4 |
98.2 |
98.4 |
98.5 |
4.46 |
| Power
When Parental Genotypes Are Not Included in Analysis, for
E(Nw) =b |
||||||||
| … |
195 |
281 |
322 |
341 |
350 |
358 |
||
| 0 | … | .1 | .1 | .2 | .2 | .0 | .0 | .02 |
| 25 | … | 1.2 | 2.3 | 2.7 | 2.3 | 1.6 | 1.8 | 1.11 |
| 50 | … | 12.8 | 18.7 | 22.6 | 23.5 | 25.2 | 23.1 | 2.25 |
| 75 | … | 44.3 | 64.1 | 69.5 | 71.5 | 73.5 | 73.9 | 3.34 |
| 100 | … | 83.3 | 94.6 | 97.3 | 97.7 | 98.0 | 98.3 | 4.45 |
Note.— Each simulated data set consisted of 480 total offspring, so that the total number of families decreased with increasing sibship size.
Between QTL and marker locus (θ=0). The total trait variance was set at 100, so that the true additive genetic value at the QTL was 4.47.
Power is shown as the proportion of simulations exceeding the nominal significance level, .001. The simulation parameters specified a QTL locus with h2=.1 and a residual sibling correlation s2=.3. Nw = effective sample size, which corresponds to offspring in families in which allelic transmission could be scored.
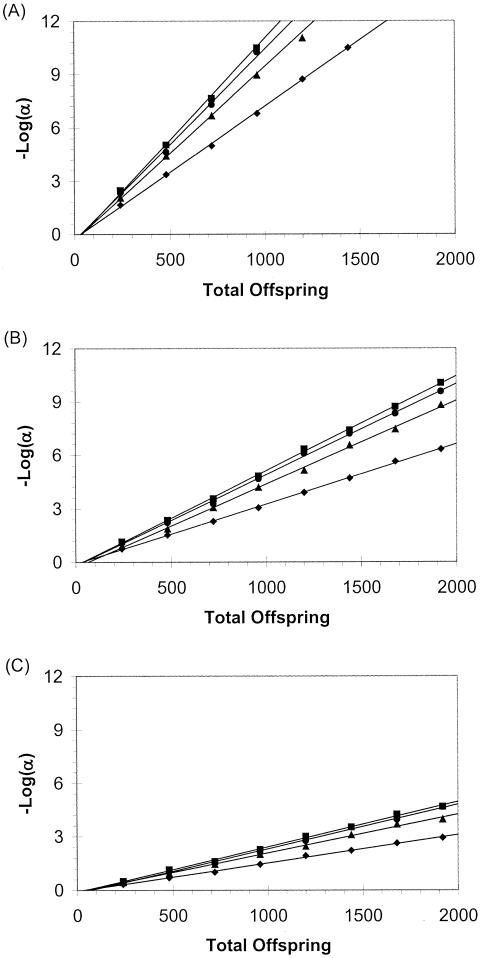
Figure 1.
Sensitivity of the orthogonal test to association. Sensitivity is
defined as
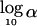 ,
where α is the significance level exceeded by 80% of simulated data
sets. The total number of offspring varied between 240 and 1,920 (in
increments of 240 children). Results were plotted for sib-pair
families in which parental genotypes were available for analysis
(squares) and for sib-pair (diamonds),
sib-triad (triangles), and sib-quad
(circles) families in which parental genotypes were not
available for analysis. The proportion of phenotypic variance attributable
to residual sibling resemblance (s2) was .30. The
major-gene effect (h2) was .10 in panel
A, .05 in panel B, and .025 in panel
C, Each plotted data point corresponds to 1,000 simulated data
sets. For convenience, a least-squares straight line has been
plotted through each set of data points.
,
where α is the significance level exceeded by 80% of simulated data
sets. The total number of offspring varied between 240 and 1,920 (in
increments of 240 children). Results were plotted for sib-pair
families in which parental genotypes were available for analysis
(squares) and for sib-pair (diamonds),
sib-triad (triangles), and sib-quad
(circles) families in which parental genotypes were not
available for analysis. The proportion of phenotypic variance attributable
to residual sibling resemblance (s2) was .30. The
major-gene effect (h2) was .10 in panel
A, .05 in panel B, and .025 in panel
C, Each plotted data point corresponds to 1,000 simulated data
sets. For convenience, a least-squares straight line has been
plotted through each set of data points.
When D/Dmax>50%, it is possible to achieve considerable power for loci accounting for 10% of the phenotypic variance, and estimates of βw are unbiased and essentially exact when there is complete disequilibrium (table 4). The relationship between the apparent additive genetic value of the marker locus, βw, the disequilibrium coefficient, D, and additive genetic effect at the QTL is very close to amarker=aQTLD/pQTLqQTL (Falconer 1989; Fulker et al. 1999). This implies that the proportion of variance explained by the association parameter is a function of the squared disequilibrium coefficient D2 and the additive genetic variance of the trait locus, so that it is not surprising that power is very sensitive to D. When D=Dmax and the QTL and marker-allele frequencies are the same, all of the genetic variance attributable to the QTL will be encompassed in the allelic-association parameter, and estimates of the residual additive genetic variance (σ2a) will equal 0.
Figure 1 shows the most
stringent significance level, α, that can be applied when 80% power
is achieved, as a function of both the total number of offspring sampled
and the additive genetic variance of the QTL, when the trait locus is
observed. As noted previously, when parental genotypes are available, power
does not depend greatly on the number of offspring in each family, so that
only the sib-pair case has been plotted. When parents are
unavailable, it is clear that achievable significance levels rapidly
approach that of the case in which parents are available, as the number of
children in each family increases. When these plots are used, an arbitrary
significance level may be selected for a given sample size and study
design. Alternatively, for a desired number of independent tests and
correspondingly adjusted significance level, an appropriate sample size and
study design may be selected. For example, for the hypothetical genome
screens proposed by Risch and Merikangas
(1996),
α=5×10-8 and
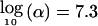 ,
so that, as can be seen in
figure 1A, either
∼350 sib pairs with parents (700 total offspring but 1,400 genotypes)
or ∼500 sib pairs without parental information (1,000 total
offspring/genotypes) or ∼260 sib trios without parents (800 total
offspring/genotypes) are needed for 80% power and a locus that accounts for
10% of phenotypic variance. It is noteworthy that the total number of
genotypes required is smaller when parental information is not used. In
practice, the marker locus and trait locus will often not be identical, so
these represent best-case estimates of power.
,
so that, as can be seen in
figure 1A, either
∼350 sib pairs with parents (700 total offspring but 1,400 genotypes)
or ∼500 sib pairs without parental information (1,000 total
offspring/genotypes) or ∼260 sib trios without parents (800 total
offspring/genotypes) are needed for 80% power and a locus that accounts for
10% of phenotypic variance. It is noteworthy that the total number of
genotypes required is smaller when parental information is not used. In
practice, the marker locus and trait locus will often not be identical, so
these represent best-case estimates of power.
Evaluation of the Permutation Test
To assess the performance of the permutation test, a series of simulations was undertaken in which dominance variance was introduced to skew the phenotypic distribution and to violate multivariate normality. In an attempt to introduce further departures from asymptotic expectations, we omitted the appropriate dominance-variance parameter from the variance-components portion of the model. The results of these simulations are presented in table 5. The performance of the empirical permutation test was examined in 5,000 samples of 120 offspring (in families with 1 to 8 children) when a dominant major gene (H2=.3, s2=.3) was segregating (θ = 0). When D=0, the overall error rate at the .05 significance level was .06 when asymptotic expectations were used but was .05 when empirical significance levels were calculated from 1,000 permutations of each data set. When D=Dmax, power at the .05 significance level was 56% for asymptotic significance levels but was 52% when empirical significance levels were calculated from 1,000 permutations of each data set. For larger samples in which the model is well specified, such as those in table 4, we find no significant advantages in this permutation test.
Table 5.
Error Rates When the Variances Model for Ωijk Is Inappropriate
|
Error
Rate when Total No. of
Offspring Isa |
|||||
| Offspring per Family | 120 | 240 | 480 | 960 | 1,920 |
| When Parental Genotypes Are Available | |||||
| 1 | 5.9 | 5.6 | 5.2 | 5.1 | 5.2 |
| 2 | 6.3 | 5.2 | 5.5 | 5.3 | 5.8 |
| 4 | 6.3 | 5.2 | 5.5 | 5.3 | 5.6 |
| 8 | 6.9 | 6.6 | 6.2 | 5.9 | 5.5 |
| When Parental Genotypes Are Not Available | |||||
| 2 | 7.0 | 5.7 | 5.8 | 5.2 | 5.7 |
| 4 | 6.5 | 6.6 | 6.1 | 6.3 | 6.2 |
| 8 | 8.6 | 7.0 | 6.2 | 6.1 | 5.5 |
Proportion of simulations exceeding the nominal .05 significance level when there is a linked dominant major gene (θ=0, h2=.3) with equally frequent alleles. The model for variances in Ωj did not include a dominance variance component, so that in larger families the error rate is high. This major gene also introduced skewness in the phenotype distribution, violating multivariate normality.
Discussion
The orthogonal model that we propose is a generalization of the one described by Fulker et al. (1999) for sib-pair data. It allows for the optional inclusion of parental data, which greatly increases power, and for the analysis of larger sibships, in which identification of segregating alleles is more efficient. For large sample sizes or when empirical significance levels are calculated by the permutation method described, the test is robust to a variety of biases, including linkage, background familiality, and population stratification. Also, when parental data are used, the test of the within-family–association parameter βw is asymptotically a test of E(wy)=0 and is equivalent to that described by Rabinowitz (1997) without the benefit of the variance-components framework. Other linear models, such as that proposed by Allison (1997), could be used with the variance-components approach, but the orthogonal model is attractive because it both provides direct estimates of the additive genetic value of the marker alleles and can be used when parental genotypes are unavailable. It is important to emphasize that the present approach treats linkage and association separately. Consequently, in contrast to other methods, which provide tests of disequilibrium only in minimal family configurations (Spielman et al. 1993; Allison 1997; Rabinowitz 1997; Allison et al. 1999), the orthogonal method does not detect linkage in the absence of disequilibrium in nuclear families of any configuration.
Although, in our simulations, power depended mostly on the major-gene–effect size and on the total number of offspring available for analysis, in practice it is undesirable to rely on a small number of large families, because they might represent very few alleles. However, moderate-size families (i.e., three to four sibs) might be more attractive than sib pairs, because they provide much greater power when parents are not available and require less genotyping effort when parents are available. The observation that, for multiplex families, the number of individuals that need to be genotyped in order to achieve comparable power is smaller when parental genotypes are not used is important in situations in which genotyping capacity is limited.
Obviously, power is very sensitive to disequilibrium, so that this test and other, related approaches are well suited for the analysis of dense maps. In practice, it may not be practical to use these dense maps for genome screens, but they can be used to follow up suggestive linkages that have been identified by allele-sharing methods on a more sparse map. When a dense marker map becomes available, it can be used to produce multipoint estimates of IBD. In the variance-components side of the model, better IBD estimates allow the fitted variance-covariance matrix to better approximate the true variances and covariances, improving the performance of the model, in terms of both power and error rates.
The model can be easily extended to allow for multiallelic markers with up to X alleles, by inclusion of a separate between- and within-family component for alleles 1 through X-1, and, in this situation, no changes to the variance model should be required. In other situations, it might be appropriate to define either dominance genotype scores or, when imprinting is suspected, separate paternal and maternal genotype scores. These alternative genotype scores can be decomposed into orthogonal components by taking either the sibling average or its asymptotic expectation derived from the parental genotypes. However, these modifications require either changes to the variance model or calculation of empirical P values, by analogous permutation tests.
Hopper and Mathews (1982) have described a number of methods for verifying that multivariate normality assumptions are not grossly violated. The permutation test that we describe should allow this orthogonal model to be applied in situations in which multivariate normality is violated—for example, when the sample size is small or the trait distribution has been skewed by selection (e.g., see Allison 1997) or when the model for variances may be inappropriate. However, asymptotic significance levels are still appropriate in most situations examined here and can be a useful tool in prescreening, to conserve computing resources.
Acknowledgments
We wish to thank Dr. Dan Weeks for helpful comments on an early version of the manuscript. This work has been funded by the Wellcome Trust. G.R.A. is supported by a Wellcome Trust Prize Studentship. W.O.C.C. is a Wellcome Trust Senior Clinical Research Fellow. QTDT, a computer program implementing the orthogonal test of association described herein, is available at the Wellcome Trust Centre for Human Genetics Website.
Appendix A: E(βa) with Allowance for Population Admixture
Consider population admixture by defining μi and pi and qi as the phenotypic mean and the marker-allele frequencies for the population from which family i was drawn (allowing for up to K different subpopulations). Assume that within each subpopulation there is random mating and random transmission of parental alleles to offspring and that the total sample of N individuals is centered on mean 0, so that μ=Σniμi=0. In this situation,
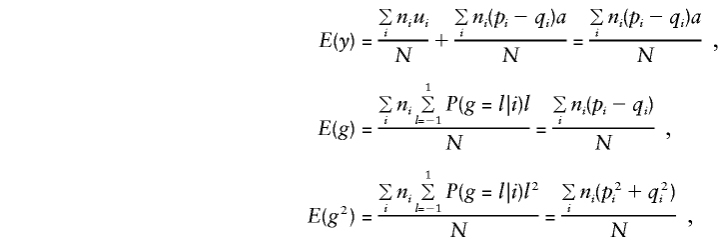 |
and
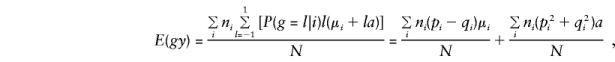 |
so that, for model (3), when the standard expectations Vx=E(x2)-E(x)2 and Cx,y=E(xy)-E(x)E(y) are used, for any x and y,
 |
where
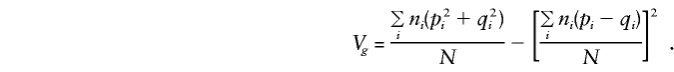 |
These expectations extend those of Cardon (in press).
Appendix B: E(βb) and E(βw) with Use of Parental Genotypes
For the orthogonal model in equation (5), the expectations for Vb, Vw, Cb,y, and Cw,y are required for solution of the normal equations and to obtain expectations for the regression parameters βw and βb.
Let Σz denote the sum over all possible mating types z and note that E(y), E(g), E(g2), and E(gy) are as given in Appendix A. Then, when the mating type frequencies given by Haseman and Elston (1972) are used,
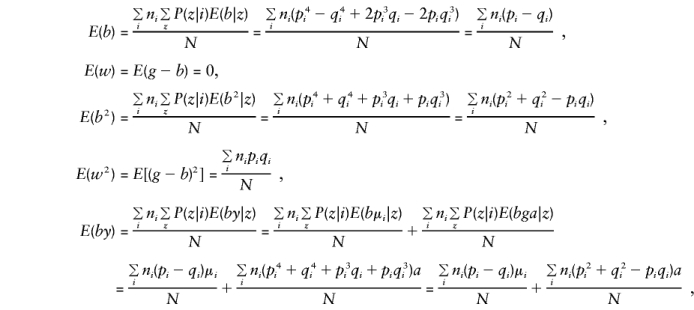 |
and
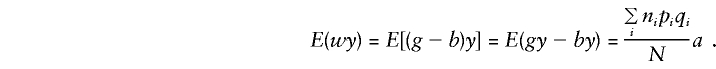 |
These are all the quantities required in order to determine
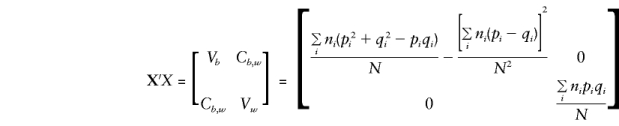 |
and
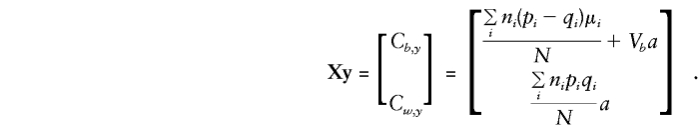 |
So, on inversion and multiplication,
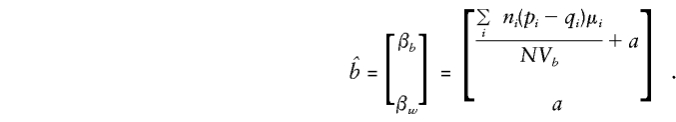 |
Appendix C: E(βb) and E(βw) with Use of Sibling Genotypes Only
When one parent is heterozygous, consider allelic transmission t∼ binomial (ni, 1/2), so that E(t2)=( 1/4)(n2i+ni). When the heterozygous and homozygous parents transmit the same allele t times, |b|=t/ni. Thus, for any family i,
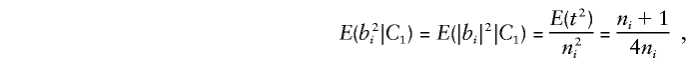 |
where C1 denotes the condition that exactly one parent is heterozygous.
To calculate E(by), it is convenient to separate y into its orthogonal-mean, μ, and major-gene, ga, components. Recall that bi=(1/ni)Σjgij, so that, when one parent is heterozygous, the major-gene component is
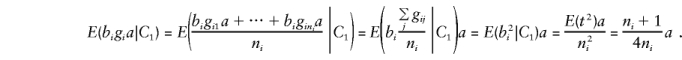 |
When two parents are heterozygous, consider allelic transmission t′∼ binomial (2ni, 1/2), so that E(t′)=ni and E(t′2)=( 1/4)(4n2i+2ni). When allele 1 (or 2) is transmitted t′ times, |b|=|t′/ni-1|. So, for any family i,
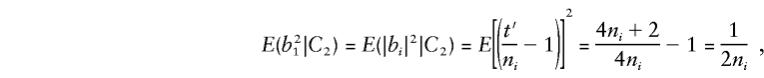 |
and the major-gene component of E(by) is
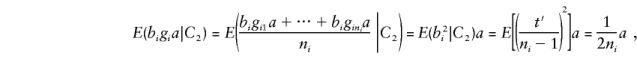 |
where C2 denotes the condition that both parents are heterozygous.
When C1 and C2 are considered, together with E(y), E(g), E(g2), and E(gy) given in Appendix A, and the mating-type frequencies
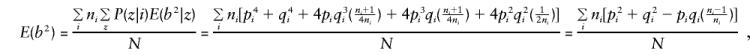 |
and
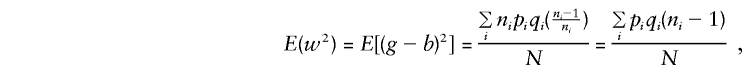 |
and, when the component derivations of E(by) are used,
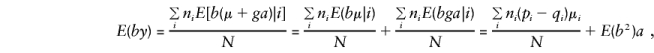 |
and
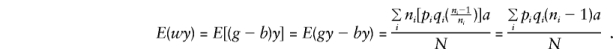 |
Thus,
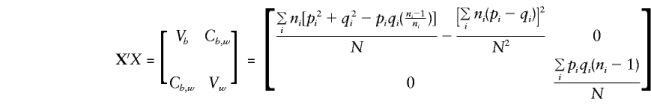 |
and
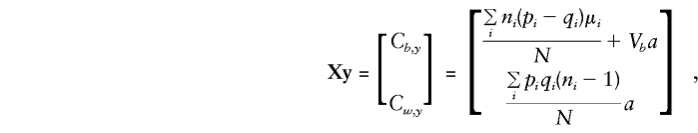 |
so that
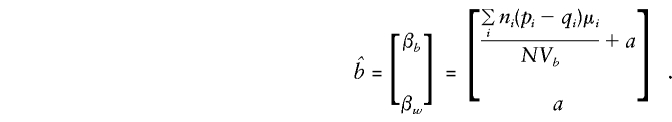 |
Electronic-Database Information
The URL for data in this article is as follows:
- The Wellcome Trust Centre for Human Genetics, http://well.ox.ac.uk (for QTDT computer program)
References
- Allison DB (1997) Transmission-disequilibrium tests for quantitative traits. Am J Hum Genet 60:676–690 [PMC free article] [PubMed]
- Allison DB, Heo M, Kaplan N, Martin ER (1999) Sibling-based tests of linkage and association for quantitative trait. Am J Hum Genet 64:1754–1763 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos CI, Zhu DK, Boerwinkle E (1996) Assessing genetic linkage and association with robust components of variance approaches. Ann Hum Genet 60:143–160 [DOI] [PubMed]
- Cardon LR. A sib pair regression model of linkage disequilibrium for quantitative traits. Hum Hered (in press) [DOI] [PubMed] [Google Scholar]
- Chakravarti A (1998) It's raining SNPs, hallelujah? Nat Genet 19:216–217 [DOI] [PubMed]
- Collins FS, Guyer MS, Chakravarti A (1997) Variations on a theme: cataloging human DNA sequence variation. Science 278:1580–1581 [DOI] [PubMed]
- Curtis D (1997) Use of siblings as controls in case-control association studies. Ann Hum Genet 61:319–333 [DOI] [PubMed]
- Curtis D, Sham PC (1995) A note on the application of the transmission disequilibrium test when a parent is missing. Am J Hum Genet 56:811–812 [PMC free article] [PubMed]
- Falconer DS (1989) Introduction to quantitative genetics. Longman Scientific & Technical, London [Google Scholar]
- Fulker DW, Cherny SS, Sham PC, Hewitt JK (1999) Combined linkage and association analysis for quantitative traits. Am J Hum Genet 64:259–267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- George VT, Elston RC (1987) Testing of association between polymorphic markers and quantitative traits in pedigrees. Genet Epidemiol 4:193–201 [DOI] [PubMed]
- Haseman JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 [DOI] [PubMed]
- Hopper JL, Mathews JD (1982) Extensions to multivariate normal models for pedigree analysis. Ann Hum Genet 46:373–383 [DOI] [PubMed]
- Kruglyak L (1997) The use of a genetic map of biallelic markers in linkage studies. Nat Genet 17:21–24 [DOI] [PubMed]
- Lander E (1999) Array of hope. Nat Genet 21:3–4 [DOI] [PubMed]
- Lewontin RC, Kojima K (1960) The evolutionary dynamics of complex polymorphisms. Evolution 14:450–472 [Google Scholar]
- Martin ER, Kaplan NL, Weir BS (1997) Tests for linkage and association in nuclear families. Am J Hum Genet 61:439–448 [DOI] [PMC free article] [PubMed]
- Rabinowitz D (1997) A transmission disequilibrium test for quantitative trait loci. Hum Hered 47:342–350 [DOI] [PubMed]
- Risch N, Merikangas K (1996) The future of genetic studies of complex human diseases. Science 273:1516–1517 [DOI] [PubMed]
- Searle SR, Casella G, McCulloch CE (1992) Variance components. In: Wiley series in probability and mathematical statistics. John Wiley & Sons, New York [Google Scholar]
- Spielman RS, McGinnis RE, Ewens WJ (1993) Transmission test for linkage disequilibrium: the insulin gene region and insulin-dependent diabetes mellitus (IDDM). Am J Hum Genet 52:506–516 [PMC free article] [PubMed]
- Wan Y, Cohen J, Guerra R (1997) A permutation test for the robust sib-pair linkage method. Ann Hum Genet 61:79–87 [DOI] [PubMed]
- Weinberg CR, Wilcox AJ, Lie RT (1998) A log-linear approach to case-parent-triad data: assessing the effects of genes that act either directly or through maternal effects and that may be subject to parental imprinting. Am J Hum Genet 62:969–978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittaker JC, Thompson DJ (1999) Finite-sample properties of family-based association tests. Am J Hum Genet 64:910–915 [DOI] [PMC free article] [PubMed]