Recombinational and Mutational Hotspots within the Human Lipoprotein Lipase Gene

Summary

Here an analysis is presented of the roles of recombination and mutation in shaping previously determined haplotype variation in 9.7 kb of genomic DNA sequence from the human lipoprotein lipase gene (LPL), scored in 71 individuals from three populations: 24 African Americans, 24 Finns, and 23 non-Hispanic whites. Recombination and gene-conversion events inferred from data on 88 haplotypes that were defined by 69 variable sites were tested. The analysis revealed 29 statistically significant recombination events and one gene-conversion event. The recombination events were concentrated in a 1.9-kb region, near the middle of the segment, that contains a microsatellite and a pair of tandem and complementary mononucleotide runs; both the microsatellite and the runs show length variation. An analysis of site variation revealed that 9.6% of the nucleotides at CpG sites were variable, as were 3% of the nucleotides found in mononucleotide runs of ⩾5 nucleotides, 3% of the nucleotides found ⩽3 bp from certain putative polymerase α–arrest sites, and 0.5% of the remaining nucleotides. This nonhomogeneous distribution of variation suggests that multiple mutational hits at certain sites are common, an observation that challenges the fundamental assumption of the infinite-sites–mutation model. The nonrandom patterns of recombination and mutation suggest that randomly chosen single-nucleotide polymorphisms may not be optimal for disequilibrium mapping of this gene. Overall, these results indicate that both recombinational and mutational hotspots have played significant roles in shaping the haplotype variation at the LPL locus.

Introduction

Coronary artery disease (CAD) is the major cause of death in many countries, and genetic factors play a significant role in determining CAD risk (Sing and Skolnick 1979; Carter et al. 1984; Sing et al. 1995). Because of its central role in regulation of lipid metabolism (Funke and Assman 1995; Fisher et al. 1997), the human lipoprotein lipase gene (LPL) is a candidate for influencing the risk of CAD. To investigate the impact that variation in LPL has on interindividual variation in CAD-related phenotypes, we have sequenced 71 individuals from three populations, for a 9.7-kb region of this gene (Nickerson et al. 1998). Nickerson et al. (1998) described 88 variable sites in the sequenced segment, and Clark et al. (1998) described the haplotype structure of that variation. Ultimately, we wish to use these data for tests of association between observed DNA polymorphism and phenotypic variation both in CAD and in intermediate phenotypes (such as blood cholesterol levels) in the general, rather than the clinical, population. Optimal methods of analysis of genotype-phenotype associations depend on the relative roles of mutation and recombination as sources of haplotype variation at the candidate locus. For example, Long et al. (1998) and Lyman and Mackay (1998) present methodologies that work well when there is much recombination relative to mutations, whereas Templeton et al. (1987), Templeton and Sing (1993), and Templeton (1996) present methods that work well when recombination is rare relative to mutation. In this study, we extend the analysis of LPL variation to quantifying the roles of mutation and recombination in structuring the observed pattern of molecular genetic variation.

Ideally, one should simultaneously estimate recombination events and mutational phylogeny, because haplotype variation is shaped by both an interwoven combination of accumulated mutational changes within haplotype lineages and recombination/gene conversions among these lineages. Two avenues have been proposed to accomplish this task. The first finds the most parsimonious history for subregions of the sequence under study and then detects recombination through phylogenetic incompatibilities among these different subregions (Hein 1990; Hein 1993; Robertson et al. 1995a, 1995b; Jakobsen et al. 1997). A second avenue constructs a null hypothesis on the basis of the phylogenetic concept of homoplasy (Crandall and Templeton 1999). For the purposes of this study, apparent homoplasy refers to the occurrence of multiple changes at a single site within a phylogeny. True homoplasies arise when the same nucleotide site experiences multiple mutational hits. Recombination creates the appearance of homoplasy when a phylogeny is estimated under the null hypothesis of no recombination. However, the homoplasies created by recombination are clustered together on the DNA molecule, whereas true homoplasies are not. The algorithm of Crandall and Templeton (1999) tests homoplasies for clustering under the null hypothesis of no recombination. Significant rejections of the null hypothesis lead to an inference of recombination and/or gene-conversion events.

Although, a priori, true homoplasy may seem unlikely when one deals with sequences with diversity levels that are well below mutational saturation, multiple hits could occur if a small subset of sites have an unusually high rate of mutation. Several studies indicate that most mutations in human DNA come from a small number of highly mutable sites. Approximately one-third of all mutations in human nuclear DNA are transitions from 5-methylcytosine to thymine (Rideout et al. 1990; Jones et al. 1992; Magewu and Jones 1994; Krawczak et al. 1995; Yang et al. 1996; Schmutte and Jones 1998). Methylated cytosines occur exclusively at CpG dinucleotides, which are markedly underrepresented in human DNA, relative to their expected frequencies under the hypothesis of independence of each nucleotide state and relative to all other dinucleotide states. Mutational hotspots have also been reported for mononucleotide-repeat regions, DNA polymerase α–arrest sites, and other rarely occurring motifs in human DNA (Krawczak and Cooper 1991; Todorova and Danieli 1997; Nakagawa et al. 1998; Tvrdik et al. 1998). Multiple mutational hits are therefore possible, as has been inferred for some highly mutable sites (Reiss et al. 1991; Krawczak et al. 1995). Under selective neutrality, the amount of variation at a site should increase with its mutation rate. Hence, mutational hotspots should have an increased chance of segregating variation in a population. We will test for mutational hotspots by examining the distribution of the observed variable sites across categories identified as potentially highly mutable in the mutation studies cited above. Overall, we intend to document the roles of both recombination and mutation in the creation of apparent homoplasies and in the shaping of the haplotype variation observed in LPL.

Material and Methods

Population Samples and DNA Sequencing

We use the data of Nickerson et al. (1998) and Clark et al. (1998) on three human samples of unrelated individuals: (1) a Jackson, MS, sample (n=24) that is part of an ongoing National Heart, Lung and Blood Institute study of hypertension in African Americans, (2) a sample from the FINRISK study from North Karelia (n=24), an area in eastern Finland that has had the world's highest known CAD risk (Tunstall-Pedoe et al. 1994), and (3) a sample from the Rochester Family Heart Study (n=23), a study of cardiovascular disease risk in the Rochester, MN, area.

DNA sequencing was performed on diploid genotypes, according to procedures described in detail by Nickerson et al. (1998). Extensive confirmatory resequencing and data-validation procedures were followed (Clark et al. 1998; Nickerson et al. 1998). Nickerson et al. (1998) published information on a total of 88 variable sites in the 9.7-kb region.

Haplotypes were determined by a mixture of allele-specific PCR (AS-PCR) and the haplotype-subtraction algorithm of Clark (1990), followed by extensive confirmatory analyses (Clark et al. 1998). Length variation at a tetranucleotide repeat was excluded from haplotype determination, since this variation does not fall under the same evolutionary models as do the other variable sites (Clark et al. 1998). Clark et al. (1998) determined the linkage phase of 69 of the remaining 87 variable sites for which the rarer variant was found in at least three chromosomes. These 69 variable sites (table 1table 1) determined a total of 88 distinct haplotypes (Clark et al. 1998).

Table 1.

Sequence Variants Used to Define Haplotypes in the LPL Locus

Sitea	Positionb	Variantc
1	106	C→A
2	110	A→C
3	145	G→A
4	325	T→C
5	343	(TG)3→(TG)4
6	479	T→C
7	551	(A)3→(A)2
8	736	T→C
9	1216	C→G
10	1220	T→C
11	1286	C→T
12	1547	A→C
13	1571	C→G
14	1828	C→G
15	1939	A→G
16	2131	C→T
17	2500	G→A
18	2619	A→G
19	2987	T→G
20	2996	C→A
21	3022	G→A
22	3248	C→G
23	3290	(T)7→(T)8
24	3297	(A)4→(A)5
25	3609	T→C
26	3723	T→C
27	3843	G→A
28	4016	C→G
29	4343	A→T
30	4346	C→G
31	4418	C→T
32	4426	T→C
33	4509	T→C
34	4576	A→T
35	4872	G→A
36	4935	T→C
37	5085	G→A
38	5168	T→C
39	5395	(A)8→(A)9
40	5441	T→C
41	5554	A→C
42	5560	A→G
43	5687	T→C
44	6250	C→T
45	6595	G→C
46	6678	T→G
47	6718	A→G
48	6772	A→G
49	6863	C→T
50	6939	delAAAT
51	7315	G→C
52	7344	A→G
53	7360	A→G
54	7413	T→C
55	7754	A→C
56	8088	insAG
57	8089	G→T
58	8285	C→G
(continued)

Table 1 (continued).

Sequence Variants Used to Define Haplotypes in the LPL Locus

Sitea	Positionb	Variantc
59	8292	A→C
60	8393	T→G
61	8533	A→C
62	8537	A→C
63	8538	(A)3→(A)2
64	8644	T→C
65	8755	G→A
66	8852	T→G
67	9402	A→G
68	9712	G→A
69	9721	G→A
a Site number assigned to each variable character used to define haplotypes in order, 5′ to 3′.
b Position in the baseline sequence (Genbank accession number AF050163).
c Substitution and insertion/deletion variants are reported as the state in the baseline sequence → alternative state (Nickerson et al. [1998]).
		(TG)3→(TG)4

Table 1.

Sequence Variants Used to Define Haplotypes in the LPL Locus. From Nickerson et al. (1998).

Sitea	Positionb	Variantc
1	106	C→A
2	110	A→C
3	145	G→A
4	325	T→C
5	343	(TG)3→(TG)4
6	479	T→C
7	551	(A)3→(A)2
8	736	T→C
9	1216	C→G
10	1220	T→C
11	1286	C→T
12	1547	A→C
13	1571	C→G
14	1828	C→G
15	1939	A→G
16	2131	C→T
17	2500	G→A
18	2619	A→G
19	2987	T→G
20	2996	C→A
21	3022	G→A
22	3248	C→G
23	3290	(T)7→(T)8
24	3297	(A)4→(A)5
25	3609	T→C
26	3723	T→C
27	3843	G→A
28	4016	C→G
29	4343	A→T
30	4346	C→G
31	4418	C→T
32	4426	T→C
33	4509	T→C
34	4576	A→T
35	4872	G→A
36	4935	T→C
37	5085	G→A
38	5168	T→C
39	5395	(A)8→(A)9
40	5441	T→C
41	5554	A→C
42	5560	A→G
43	5687	T→C
44	6250	C→T
45	6595	G→C
46	6678	T→G
47	6718	A→G
48	6772	A→G
49	6863	C→T
50	6939	delAAAT
51	7315	G→C
52	7344	A→G
53	7360	A→G
54	7413	T→C
55	7754	A→C
56	8088	insAG
57	8089	G→T
58	8285	C→G
59	8292	A→C
60	8393	T→G
61	8533	A→C
62	8537	A→C
63	8538	(A)3→(A)2
64	8644	T→C
65	8755	G→A
66	8852	T→G
67	9402	A→G
68	9712	G→A
69	9721	G→A

^aSite number assigned to each variable character used to define haplotypes in order, 5′ to 3′.

^bPosition in the baseline sequence (Genbank accession number AF050163).

^cSubstitution and insertion/deletion variants are reported as the state in the baseline sequence → alternative state.

Estimation and Testing of Recombination

We use the algorithm of Crandall and Templeton (1999) (hereafter called the “CT algorithm”) to detect recombination/gene-conversion events. The algorithm starts by estimating a haplotype “tree” under the null hypothesis of no recombination or gene conversion. We place quotation marks around the word “tree” to emphasize the fact that this “tree” may not be an accurate reflection of evolutionary history if our null hypothesis is rejected. Because different methods of phylogenetic estimation can yield different trees, we used the CT algorithm with three different tree-estimation methods—statistical parsimony, neighbor-joining, and a corrected neighbor-joining procedure—as a check for robustness to “tree” topology.

SP (Templeton et al. 1992; Crandall 1994; Crandall and Templeton 1996) favors those parsimonious solutions that avoid placement of homoplasies on short branches that lie within the “limit of parsimony” (Templeton et al. 1992). For the LPL haplotypes and with just the 69 variable sites in table 1table 1, the limit of parsimony is estimated, by equation (8) of Templeton et al. (1992), to be three mutational changes. PAUP* (Swofford 1997) was used to generate maximum-parsimony trees and then to compare the adjusted character distances with the corresponding patristic distances, to eliminate the maximum-parsimony trees that violate the limits of parsimony. We also used PAUP* to estimate an NJ “tree” on the basis of the number of site differences among haplotypes, rather than specific character states. We frequently found in the NJ “tree” mutational allocations that would not be allowed under any phylogenetic-inference method that utilizes character-state information. Hence, we imported the NJ “tree” into the program MacClade (Maddison and Maddison 1992) and then used the “full search above” option on the terminal clades in the NJ “tree,” which resulted in a corrected-NJ “tree.”

Given a “tree,” we test the null hypothesis of no recombination, by means of associations between the position of apparent homoplasies in the “tree” and the order of their physical positions in the DNA sequence. Recombination and gene conversion result in physically clustered homoplasies being placed on the same branch in the “tree.” The CT algorithm uses this association to identify putative recombinants by tracing pathways through the “tree,” to match the homoplasies clustered on a branch with their occurrences elsewhere in the “tree.” If recombination caused the cluster of homoplasies, the mutations found on this pathway would be expected to fall to one side or the other in physical position on the DNA molecule, relative to the matched homoplasies. A runs test based on a hypergeometric distribution under the null hypothesis of no recombination is used to identify statistically significant recombinants. The algorithm also identifies crossover intervals and candidate parental types. Because a recombinant only obtains part of its sequence from one parental type, the candidate parental types can vary within the sequence portion not contributed to the recombinant. The CT algorithm chooses as parentals from the candidates those haplotypes or nodes that are closest in the “tree” to the putative recombinant, a statistically conservative assumption. For more details, see the work of Crandall and Templeton (1999).

Testing of Gene Conversion

The CT hypergeometric test for recombination is a runs test based on the ideal expectation of two runs under recombination: α matched homoplasious sites from one parental type, defining a run on one end of the physical sequence, followed by a run of β sites (i.e., the mutations on the pathway interconnecting the matched homoplasies) from the other parental type, on the other end of the sequence. Gene conversion is another genetic mechanism for placing a physical cluster of nucleotide states on a new haplotype background. Gene conversion can place a small run of variable sites from one haplotype into the middle of a second haplotype, thereby resulting in three runs by physical location. Gene conversion can also result in only two runs, but such cases are indistinguishable from recombination. Therefore, some of the recombination events identified by the testing procedures given above may actually be caused by conversion events. However, because the CT test is specifically designed for detecting two runs, this test may fail to detect some gene-conversion events. Hence, after the recombination tests are performed, an additional runs test is performed to detect gene-conversion events that have resulted in three or more runs. To test gene conversion with more than two runs, α apparent homoplasies on a “branch” are matched to another region of the “tree,” with β other mutations lying on the pathway between the two “tree” regions, exactly as under the original CT algorithm as described by Crandall and Templeton (1999). The α+β mutations are then ordered by physical position, and the number of runs, say δ, of α and β mutations in the physically ordered sequence is recorded. Under the null hypothesis of no recombination/gene conversion, the probability for the number of runs is given (Mood and Graybill 1963) by

Because gene conversion is tested only after recombination (d=2), equations (1) are used to calculate the probability of δ=2 under the null hypothesis, and then equations (1) are divided by [1-Prob(δ=2)] to obtain the conditional distribution of runs, given that d⩾3—the only condition under which this gene-conversion test is used. By use of conditional probabilities, the power to detect gene-conversion events of three or more runs is lowered, relative to the power to detect recombination events or gene-conversion events that result in two runs. Given that recombination and gene-conversion events are inferred only when a null hypothesis is rejected, both tests will have type II errors in which actual recombination/gene-conversion events are undetected, because too few sites mark the event to yield significance. The problem of type I errors (false inferences of an event) and multiple comparisons is addressed in the next subsection.

Rate and Characteristics of False Positives

Because the CT algorithm uses a large number of individual statistical tests that are dependent in a complex fashion, we use a random-permutation simulation (Edgington 1986) to investigate the rate and the attributes of false positives produced by the CT algorithm. To simulate the null hypothesis of no association between position in the “tree” and physical position on the molecule of homoplasies, we randomly permute the assignments of the estimated mutational changes in the “tree” to specific branches, retaining the overall topology and branch lengths of the original “tree.” The random permutations do have to be constrained, because, with homoplasy, it is possible that the same mutational change will be placed upon a single branch—a biological impossibility. It is also possible for a mutation and its reversal to be placed on the same branch. Although not impossible, such changes are invisible and never occur on any estimated tree. Finally, a mutation and its reversal can be placed upon adjacent branches in such a manner that all character-state methods of phylogenetic inference would simply move the node before the first mutation and eliminate the reversal. Therefore, each random permutation is screened for these difficulties. When a second homoplasy is encountered that would create one of these problems, it is interchanged with the next mutation in the random vector that would eliminate this difficulty. A program in Mathematica (Wolfram 1996) was written to perform these random permutations on the SP “tree.” Each randomly permuted tree then was subjected to the same testing procedures for recombination and gene conversion as were the observed data. Because these simulations do not have any recombination events, we know the “truth” in these permuted data sets—that is, that there are no allocations of homoplasies caused by recombination events. Hence, all inferences of recombination from the permuted data sets are regarded as false positives. Random permutations were generated until the number of inferred false positives was greater than or equal to those found in the observed data to have a comparable number of false positives.

The false-positive rate of the CT algorithm is also estimated by its application to the data of Vigilant et al. (1991) for 135 haplotypes defined by 179 variable sites in 1,137 bp of human mtDNA, a molecule that does not recombine. To obtain an index of the relative false-positive rate of the CT algorithm to that of the methods previously applied to the LPL data (Clark et al. 1998), the Vigilant et al. (1991) data were also analyzed with the program DnaSP (Rozas and Rozas 1997), which is used to calculate the expected number and the minimum number of recombination events, by the methods of Hudson and Kaplan (1985), as well as the intervals in which this minimal set of crossover events occurred. Finally, this program calculates the Hudson (1987) estimator of the ratio of the number of recombination events to mutations in the evolutionary history of the sample. This same ratio is estimated by the CT algorithm by dividing the number of inferred recombination events by the total branch length of the “SP” tree minus the number of homoplasies resolved by the inferred recombination events.

Testing for Mutagenic Sites

We searched the sequences (both strands) for the following potentially hypermutable motifs: CG dinucleotides, mononucleotide runs of length ⩾5, and TG(A/G)(A/G)GA (a DNA polymerase α–arrest motif). The mutagenic effects of α-arrest sites can affect neighboring sites as well. Todorova and Danieli (1997) therefore included nucleotides ⩽5 bp away from the arrest-site motif in their analysis. We will use the more stringent criteria of being ⩽3 bp from the arrest motif.

The frequency of variable sites within each category was counted and standardized on a per-nucleotide basis. The tetranucleotide repeat at position 4823 in the GENBANK reference sequence was excluded from this analysis because of its already known high mutation rate (Nickerson et al. 1998). Of the 9,734 sites in the original reference sequence, this exclusion reduces the number of nucleotides to 9,694. The remaining 87 polymorphisms listed intable 1table 1 of Nickerson et al. (1998) were included in this analysis. Because of polymorphism, all nucleotide states that occurred at a particular site were considered, and if any of them matched one of the aforementioned motifs, the site was regarded as highly mutable. Log-likelihood–ratio tests were performed to test hypotheses about homogeneity of variation across the different site categories.

Results

Tree Estimation

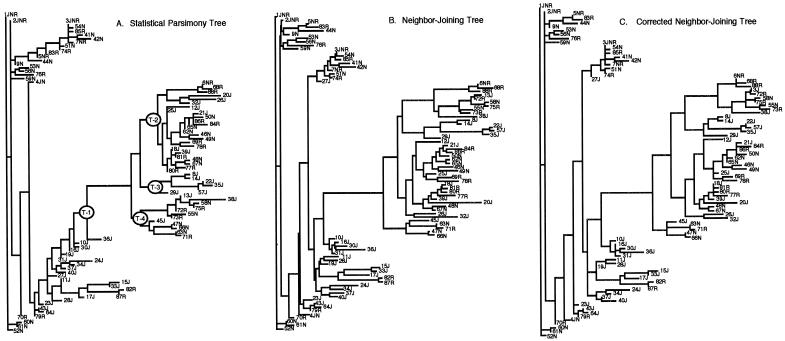
Figure 1 presents the estimated topologies and branch lengths for the SP, NJ, and corrected NJ trees. The SP and NJ methods represent qualitatively different ways of estimating “trees” (cladistic vs. phenetic), so it is not surprising that the topologies of the SP and NJ “trees” differ substantially (fig. 1). The Templeton test option in PAUP* shows that the difference between the SP and NJ “trees” is highly significant (P⩽.0035). The Templeton (1983, 1987) test also reveals differences in allocations of homoplasies at 29 of the 57 variable sites showing any homoplasy at all under either “tree.” The corrected NJ “tree” eliminated 10 homoplasies in the NJ “tree” but still had 8 more homoplasies than did the SP “tree.”

Figure 1.

Evolutionary “trees” of LPL, as estimated by three procedures. In each case, only the horizontal length of branches indicate mutational change, with the length proportional to the number of mutations on that branch. Haplotypes are indicated by a number, followed by one or more letters indicating the populations in which that particular haplotype was present (J = Jackson, N = North Karelia, and R = Rochester). A, Statistical parsimony “tree.” Nodes that define four major clades are indicated by an oval containing “T-i,” where i can be 1, 2, 3, or 4. There are actually 8 “trees” in the statistically parsimonious confidence set, but the differences from the one portrayed here are minor. The full set of SP trees is available at the MDECODE Web site. B, NJ “tree.” C, Corrected NJ “tree.”

Detection of Statistically Significant Recombination and Gene-Conversion Events

Twenty-nine recombination events with tail probabilities <.05 were detected by use of the SP “tree.” Details for each of these 29 recombination events can be obtained at the MDECODE Web site. Each recombination event is assigned a number (1–29), and all subsequent references to a particular recombination event use the numbers given at this Web site. One statistically significant gene-conversion event (P⩽.0011) was detected with three or more runs. This conversion event spanned four variable sites (6, 14, 15, and 18) found on the two widely separated branches going to haplotypes 33J and 20J (fig. 1). In sum, 30 significant recombination or gene-conversion events were detected by the analysis using the SP “tree.”

The analysis using the NJ “tree” detected the same gene-conversion event. Of the 29 recombination events detected in the SP analysis, 2 were not detected in the NJ analysis: events 23 and 24. The remaining 27 events were detected—but, in some cases, not in an identical fashion. For events 4, 6–12, 14, 21, 22, 25, and 29, the parental haplotypes (all inferred nodes in the “tree,” rather than haplotypes in the sample) were different. This result is not surprising, because many haplotypes or nodes can usually serve as parentals and still be consistent with the inferred recombination event. Because the topology of the NJ “tree” was very different from that of the SP “tree,” the CT algorithm identified different parental nodes as closer in the NJ “tree” to the putative recombinant in these cases. These differences do not indicate any biological incompatibility. A more important difference is that the NJ “tree” tended to group into a single clade what are distinct recombinant clades in the SP “tree.” In particular, the NJ analysis grouped together recombination events 3 and 15; 16–18, and 20; and 26 and 28. Two of these combinations (16 and 20; 26 and 28) involved situations in which the recombinant of one event was the parental in the second event in the SP analysis. The remainder involved recombination events that the SP analysis indicated shared one common parental type. Finally, the NJ analysis inferred four new recombination events not detected in the SP analysis.

The corrected NJ “tree” eliminated two of the four recombination events unique to the NJ analysis, split events 3 and 15 back into two events, and split the NJ combination of events 16–18, and 20 into three events (16 and 20; 17; 18). In summary, 28 of the 30 events in the SP analysis were explained by 26 events in the corrected NJ analysis, with 2 events unique to each analysis.

Characterization of False-Positive Rate and Attributes

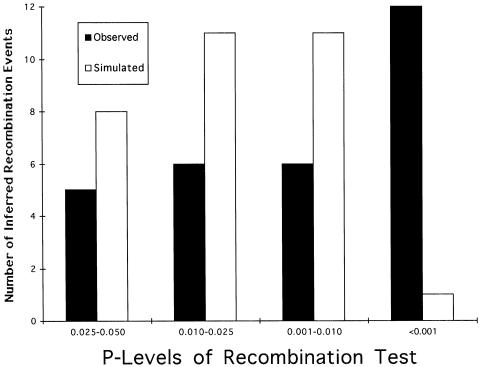
Ten runs of random permutations were needed to obtain 31 false positives, all of which were recombination events. These 31 false positives were then contrasted to the 30 events inferred under the SP analysis. The number of false positives per simulation varied from two to six (fig. 2). The events inferred in the simulated and SP analyses were contrasted for the run lengths of matched homoplasies (fig. 3), tail probabilities (fig. 4), and the distribution of possible crossover-event intervals over the region sequenced (fig. 5).

Figure 2.

Number of false positives under the CT algorithm for inferring recombination events in 10 random permutations of variable-site position across phylogenetic position in the “tree” given in figure 1A.

Figure 3.

Run length of matched homoplasies for 31 false positives under the CT algorithm for inferring recombination events in 10 random permutations of variable-site position across phylogenetic position in the “tree” given in figure 1A.

Figure 4.

Tail probabilities for 31 false positives of the CT hypergeometric test of recombination in 10 random permutations of variable-site position across phylogenetic position in the “tree” given in figure 1A.

Figure 5.

Physical distribution of 31 false positives for recombination in 10 random permutations of variable-site position across phylogenetic position in the “tree” given in figure 1A, and physical distribution of 29 recombination events inferred from the observed data. For each variable site in table 1table 1, the number of recombination events inferred from the observed and permuted data whose potential crossover intervals overlapped that site are indicated on the Y-axis.

Seven false positives were detected in the mtDNA data set of Vigilant et al. (1998) by use of the CT algorithm. Six of these false positives had α=2 (where α is the length of the run of matched homoplasies that define a recombination event), and one had α=3. The P levels varied from .0476 to .001 (the event with α=3). Six of the false positives had inferred crossover intervals close to one end of the sequence or the other, with only the least-supported inference having an interval close to the center (α=2, β=5, and P⩽.0476, with the inferred crossover occurring between positions 234–359 in the 1,137 bp sequenced). The estimated ratio of recombination events to mutational events for mtDNA was .016, versus a true value of 0.

When the mtDNA data were analyzed by the program DnaSP, 413 recombination events were estimated, by means of the procedure of Hudson and Kaplan (1985), to have occurred, with a uniform distribution of crossover intervals over the molecule. The estimated ratio of the number of recombination to mutational events in the evolutionary history of this sample of mtDNA molecules was 7.803, when the estimator of Hudson (1987) was used.

Distribution of Variable Sites over Putative Mutagenic and Remaining Nucleotides

In the 9,694 nucleotide positions examined, 99 CG-dinucleotide motifs were encountered. Since both positions in a CG dinucleotide are subject to the mutagenic effects of a potentially methylated cytosine, these 99 sites correspond to 198 nucleotides. Of these, 19 were variable, yielding a .0960 frequency of variable CG-nucleotide sites. Of these 19 variable sites, 15 were the type of variation most strongly associated with methylated-cytosine mutagenesis—that is, either CG→TG or CG→CA transitions, when both strands are considered.

Four hundred fifty-six base pairs were found within mononucleotide runs of length ⩾5, and 15 of these sites were variable, for a frequency of .0329. One site (at position 8089 in the reference sequence) was associated with both a mononucleotide run and a CG dinucleotide and was polymorphic: C(C/G)GGGGGGG. This was one of the four CG-dinucleotide sites that did not display the type of polymorphism commonly expected from methylated-cytosine mutagenesis.

Twenty-two sites were found that had the polymerase α–arrest site motif of TG(A/G)(A/G)GA. Since we included as potentially highly mutable any nucleotide either within such a motif or ⩽3 bp from it, these 22 sites included 264 bp. Eight variable sites were found within these 264, for a frequency of .0303.

Collectively, these three potentially mutagenic motifs contain 41 of the 87 variable sites and cover 917 bp. (These figures take into account the overlap, noted above, of one CG site with one run of G's). The remaining 46 mutations are therefore found among 8,777 sites, for a frequency of .0052 per nucleotide.

The log-likelihood–ratio test of the null hypothesis that all nucleotides have the same frequency of variation was 99.1 with 3 df (a tail probability of 2.5 × 10⁻²¹). We next tested the hypothesis that the three classes of highly mutable sites have a homogenous frequency of variation. That log-likelihood–ratio test is 12.3 with 2 df (the tail probability is .002), and this rejection is due to the increased variation at CG sites (.0960) versus that at the remaining two categories of highly mutable sites (.0329 and .0303).

Discussion

Amount of Recombination

Twenty-nine recombination events were inferred with the SP “tree” and one gene-conversion event. Given the substantial differences between the SP, NJ, and corrected NJ “trees,” the “trees” shown in figure 1 provide an excellent basis for determining the robustness of the recombination inferences to “tree” topology. In this regard, the greatest discrepancy was between the SP and NJ methods. The NJ “tree” contained many mutational allocations that made no sense under any scheme of phylogenetic reconstruction that takes into account character-state information. These NJ mutational allocations caused much of the discrepancy with the SP results. First, the NJ “tree” had more homoplasies overall than did the SP tree, making false positives more likely under the CT algorithm. Two of the recombination events unique to the NJ analysis were eliminated in the corrected NJ analysis, which reduced the total number of homoplasies by 10. Second, the NJ analysis often combined recombination events that were distinct in the SP analysis. When multiple recombination events occur between parentals that differ by many sites, the resulting recombinants will be quite distant from either parental type, but the number of mutational differences between the SP-distinct recombinants can be small. The character-state data indicate the distinctiveness of these recombinants, but character-state data are ignored by NJ. As a consequence, these distinct SP clades are collapsed into a single NJ clade. The NJ “tree” must then invoke additional homoplasies to reverse the mutational sites that define the distinct SP events, often creating more homoplasies than were resolved by the inferred recombination. After these mutational allocations were corrected, only two NJ combinations remained in the corrected NJ “tree” (16 and 20; and 26 and 28), both involving a recombination event leading to a recombinant haplotype that was a parental in a subsequent recombination event. This indicates that nested recombination events are the least robust inference under the CT algorithm. These results also indicate that pure NJ is not a reliable method for the estimation of intraspecific haplotype trees in regions subject to recombination. On the positive side, our results indicate that most of the errors induced by NJ can be corrected by local branch swapping. We therefore conclude that only the SP “tree” and corrected NJ “tree” are appropriate for recombinational analyses. The SP and corrected NJ “trees” yield similar inferences, sharing 28 inferred-recombinant or converted haplotypes or clades—although the corrected-NJ analysis attributes these 28 recombinant/gene-converted clades to 26 events. Both analyses yield two recombination events unique to their respective “trees,” so only a small fraction of the inferred events are not robust to these different “tree” topologies.

The results noted above imply that 26–28 recombination/gene-conversion events occurred during the evolutionary history of these 142 samples of the LPL gene. Because we infer a recombination event only when there are sufficient data to reject the null hypothesis of no recombination (i.e., when there are at least six differences between the parental haplotypes), some recombination events between evolutionarily close haplotypes will not be detected when there are too few informative sites. The fact that our sample represents a pooling of three populations may accentuate this bias. With restricted gene flow, the more divergent haplotypes would have a lower probability of being heterozygous in the same individual and, therefore, of being parental types—yet these are the very same pairs of haplotypes that should have greatest power in yielding a significant recombination event. However, this pooling bias should be minor, since only 6.5% of the nucleotide diversity in these samples is attributable to among-population differences (Clark et al. 1998). However, the bias caused by the need for statistical significance remains important, so 26–28 events may be an underestimate. Balancing this, however, is the fact that these inferences of recombination were derived from a large number of nonindependent tests. This raises the issue of false positives.

The random permutations of the SP “tree” indicate that, for any given simulation, the CT algorithm infers two to six recombination events that are significant at the 5% level, with two false positives being the most likely outcome (fig. 2). Figure 4 shows that the significance levels of the false positives from the permuted data are significantly skewed toward P values higher than those for the 29 recombination events inferred from the actual data(χ²_3df=11.33, P=.010 under the null hypothesis of homogeneity of the recombination events inferred from the observed data and from the false positives with respect to P values). Hence, a simple readjustment of the significance level would eliminate many of the false positives. For example, using a 2.5% test instead of a 5% test would eliminate five events (6, 11, 12, 19, and 20).

The false positives also differ from the recombination events inferred from the actual data in the run length of the matched homoplasies used to identify the recombination event (fig. 3). Of 31 false positives, 27 have α=2, whereas, of 29 observed recombination events, only 12 have such a low α value, a highly significant difference (P<.0003, when a Fisher's exact test is used to test the null hypothesis of homogeneity of the recombination events inferred from the observed data and from the false positives with respect to α values). All of the recombination events previously identified, on the basis of P level, as potential candidates for false positives also have α=2. Finally, in their distribution over the DNA sequence, the simulated false positives differ dramatically from the observed recombination events (fig. 5). When the physical groupings shown in table 2 are used, the resulting χ² of homogeneity is 29.97 with 3 df, a result with a probability of <10⁻⁶ under the null hypothesis. As can be seen in figure 5, the observed recombination events are primarily clustered in the center of the DNA region, whereas the false positives are primarily clustered at the ends of the region, particularly at the 5′ end. These results, along with the previously noted differences in α values and P levels, imply that almost all the false positives occurred when two apparent homoplasies close to one end of the sequence were placed by chance upon a common branch in the “tree,” resulting in α=2 and a relatively high P level. When such a run of two apparent homoplasies is close to one end of the sequence, we are likely to encounter mutations only on the interior side of the sequence, even with long pathways through the “tree,” thereby increasing the odds of matching the homoplasies and inferring a false recombination event. In contrast, when two apparent homoplasies from the center of the sequenced region are placed upon a common branch, any long pathway through the “tree” has a high chance of encountering mutations on either side of the homoplasy cluster, thereby diminishing the odds of inferring a recombination event. This creates a bias of false positives toward the ends of the sequence and away from the interior. The disproportionate clustering of these false positives in the 5′ end is caused by the increased amount of apparent homoplasy that is associated with the 5′ end relative to the 3′ end in the “tree.” When physical positioning of the inferred crossover event is taken into account, only two of the five candidates previously identified as likely false positives remain as likely candidates: event 6 (P⩽.0278, α=2, crossover 16–19) and event 12 (P⩽.0278, α=2, crossover 5–9).

Table 2.

Distribution of Inferred Recombination Events from the Observed Data and from Simulated Data

		No. of Recombination Events
Quartile	Variable Sites in Quartile	Observed Data	Simulated Data
1	1–17	3	21
2	13–34	21	2
3	35–51	2	4
4	52–69	3	4

These conclusions are reinforced by the analysis of human mtDNA. Seven false-positive recombination events were detected in the mtDNA. The mtDNA is based on 179 variable sites (which determine the resolution of recombination detection), rather than 69, as for LPL. After adjustment for the number of variable sites, both the mtDNA and permuted LPL data yield a false positive rate of .04 per variable site. As in the permutation analysis, the mtDNA false positives primarily consisted of events with large P values, for which α=2, that were concentrated at the ends of the sequence. This indicates that the false-positive rate and the attributes of false positives are not strongly dependent on a particular tree or even on a particular data set. This further reinforces our conclusions that only events 6 and 12 are likely candidates for being false positives.

In contrast to the false-positive rate of .04 per variable site for the CT algorithm, the false-positive rate for the Hudson and Kaplan (1985) method is 2.31 per variable site for the mtDNA. Similarly, the estimated ratio of the number of recombinants to the number of mutations in the evolutionary history of the mtDNA sample is 7.803 when the Hudson (1987) estimator is used, versus 0.016 for the CT algorithm. Hence, the methods of Hudson and Kaplan (1985) and Hudson (1987) are poor measures of recombination under biologically realistic conditions.

In summary, the results of the random-permutation runs indicate that only events 6 and 12 are likely false positives, given the SP “tree.” Furthermore, events 23 and 24 were sensitive to the use of the SP “tree.” Eliminating these four events still leaves 25 recombination events, and the corrected-NJ analysis would reduce this number to 23. In addition, all analyses detect a gene-conversion event to yield a total of 24–26 recombination/conversion events. Hence, recombination/gene conversion is common within this region of the LPL gene and has played a major role in shaping the variation at this locus. Our results are discrepant with the inference by Clark et al. (1998), based on the Hudson (1987) estimator, that recombinational events were nearly as likely as mutational events in the evolutionary history of this sample of LPL sequences. By counting the number of mutational events left in the SP “tree” after eliminating the homoplasies caused by recombination and gene-conversion events, we now estimate that mutational events are nearly seven times more likely than recombination/conversion events (when all 30 inferred events in the SP analysis are used).

A Recombinational Hotspot

The Hudson and Kaplan (1985) procedure also implies that recombination was uniformly distributed throughout the sequenced portion of the LPL gene (Clark et al. 1998). In contrast, figure 5 shows that the inferred crossover events are clustered between variable sites 19 (2987 in the map of Nickerson et al. 1998) and 35 (4872 in the LPL map). Minor modes exist both 5′ and 3′ to this major mode of recombination. This apparent hotspot in the central part of the region cannot be an artifact of the CT algorithm, which, as shown in figure 5 and by the mtDNA analysis, is biased to allocate false positives away from the center. Moreover, the hotspot remains if we retain only the events held in common by the SP and the corrected-NJ analyses and regardless of whether 27 or 25 events are counted.

Further evidence for a recombinational hotspot comes from the observation that the long branches in the “tree” that interconnect the nodes labeled “T-1”–“T-4” in figure 1 had not a single inferred recombination event within them but had extensive recombination across them. Hence, these long branches in the “tree” seem to represent a true phylogenetic structure untouched by recombination, a subject that will be treated in more detail in another study. Also, although not shown, the chimpanzee sequence connects within these long branches (between T-1 and the node leading to T-2–T-4). Hence, evidence from both an outgroup analysis and the length of these branches suggests that the branches interconnecting these nodes are very old—yet they contain no detectable recombination events. By looking at the site positions of the mutations that interconnect T-1–T-4, we can infer in the sequence a location that displays an absence of recombination. When the sequenced interval is split into halves (sites 1–34 vs. sites 35–69), only 2 sites on these long branches are in the 5′ half, whereas 20 are in the 3′ half (χ²=14.8 with 1 df, P<.0001). These results clearly identify an area of little to no recombination, immediately 3′ to the recombinational hotspot shown in figure 5.

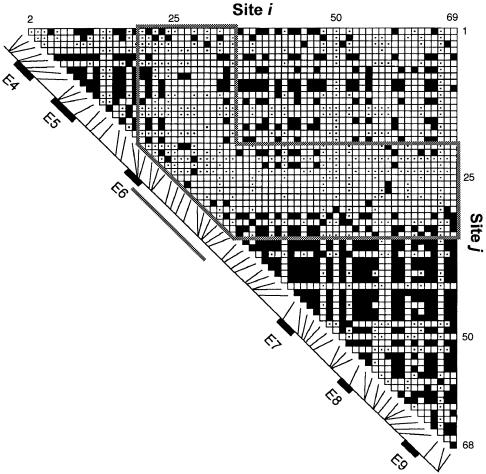
More evidence for the recombinational hotspot comes from the pattern of pairwise linkage disequilibrium reported by Clark et al. (1998). Figure 6 is a redrawing of figure 5 from Clark et al. (1998), but overlaid now with the hotspot boundaries (variable sites 19–35). The hotspot boundaries in this disequilibrium table contain an L-shaped segment that has few significant pairwise disequilibrium statistics, whereas the segments just 5′ and 3′ of this hotspot contain many significant pairwise associations. Ignoring, in figure 5 of Clark et al. (1998), all cells for which the sample sizes were to small to yield a significant disequilibrium even if absolute disequilibrium existed, one finds that, within the 5′ end, 57 (49%) of 117 pairwise disequilibrium tests were significant; in the 3′ end, 291 (59%) of 496 were significant; but, within the hotspot region and between the hotspot and the 3′ and 5′ ends, only 130 (19%) of 696 pairwise disequilibrium tests with adequate sample sizes were significant.

Figure 6.

Plot showing pairwise linkage disequilibrium, indicated by a blackened square, for site pairs with a significant Fisher's exact test (P<.001) and no correction for multiple comparisons. The labels on the X- and Y-axes indicate the site numbers, as given intable 1table 1. However, the numbers for sites 12 and 54 in table 1table 1 are not included, because their phasing was not determined. In comparisons of site pairs in which both sites have rare nucleotides, there can be complete disequilibrium (one of the four possible gametes having a count of 0)—yet the Fisher's exact test can be not significant. Site pairs that lack the power to test a significant association are indicated by a dot in the center of the square. The diagonal line, with exons 4–9 labeled, indicates the location of each varying site along the gene. The thick solid lines outline the maximal boundaries of the recombinational hotspot.

Because it has been hypothesized that runs of short repeats of nucleotides may serve as foci for recombination, we also examined the locations of repeat-length polymorphisms, relative to the hotspot. In this regard, the hotspot region contains two unique features in the 9.7 kb sequenced. First, between sites 34 and 35, a tetranucleotide-repeat polymorphism is found that is associated with more alleles than is any other site (Nickerson et al. 1998). Second, the only pair of tandem, variable mononucleotide runs exists at sites 23 and 24. Moreover, these adjacent runs consist of complementary nucleotides (a run of T's followed by a run of A's). Both of these unusual nucleotide-repeat polymorphic sites are within the recombinational-hotspot boundaries. This association does not imply causation, but this result does indicate that further work should be done on the association of these sites with the recombinational hotspot.

In summary, the evidence for a recombinational hotspot is multifaceted and strong. Thus, the results of the current analysis are discrepant with the analyses based on the procedures of Hudson and Kaplan (1985) and Hudson (1987). The Hudson and Kaplan (1985) and Hudson (1987) procedures perform poorly with human mtDNA, as has already been noted elsewhere (Hey and Wakeley 1997). Hey and Wakeley (1997) have noted that the “critical assumption” of these statistics is “the infinite sites mutation model.” This model regards true homoplasies as an absolute impossibility. The mtDNA data clearly violate the infinite-sites model (Hey and Wakeley 1997), but many researchers demonstrate an implicit belief that the infinite-sites mutation model is appropriate for nuclear DNA, by their application of infinite-sites statistics to such DNA. However, none of the studies on mutation in human nuclear DNA that have been cited in the Introduction support the infinite-sites assumption. Therefore, we need to see if the patterns of variation found at LPL are more consistent with these prior mutational studies or with the infinite-sites model.

Mutational Hotspots

Under the assumption of neutrality, the amount of variation associated with a site should increase with its mutation rate. Hence, we tested the predictions of the prior human mutational studies by examining the distribution of the observed variable sites across categories identified as potentially highly mutable in the mutation studies cited in the Introduction. The results clearly indicate that the observed frequency of polymorphic sites vary in a highly significant fashion over the four categories considered, with CG > mononucleotide runs ≈ polymerase α–arrest sites > remaining sites. We therefore conclude that the site motifs identified in the literature as highly mutable in human nuclear DNA are significantly associated with highly elevated rates of variation in the LPL region sequenced, with CpG dinucleotides showing the highest rate.

The motifs with the highest level of variation are also some of the rarest motifs in the sequence. For example, table 3 shows the frequency of all possible dinucleotide motifs in the LPL reference sequence, along with the ratio of observed to expected values, under the hypothesis that the frequency of a dinucleotide is simply the product of the component nucleotide frequencies. As can be seen, CG dinucleotides are by far the most underrepresented class. The fact that nearly 20% (19 of 99) of the CG sites are polymorphic makes it extremely likely that multiple hits have occurred. Note also that one of the traditional arguments against multiple hits—the presence of only two polymorphic nucleotide states, rather than three or four—is invalid, because methylated-cytosine mutagenesis is expected to produce polymorphic sites with only two nucleotide states (usually C/T or A/G). Consequently, much of the apparent homoplasy in the “trees” shown in figure 1 is probably true homoplasy. This possibility will be investigated in more detail in a subsequent study.

Table 3.

Number and Frequencies of All Possible Dinucleotides in the LPL Reference Sequence, and Ratio of Observed to Expected Dinucleotide Frequencies^[Note]

Dinucleotide	No. (Frequency)	Observed Frequency/Expected Frequency
TT	1,024 (.105)	1.15
TC	594 (.061)	.98
TA	640 (.066)	.75
TG	684 (.070)	1.16
CT	697 (.072)	1.15
CC	511 (.052)	1.23
CA	716 (.074)	1.23
CG	88 (.009)	.22
AT	739 (.076)	.87
AC	483 (.050)	.83
AA	890 (.091)	1.09
AG	709 (.073)	1.25
GT	481 (.049)	.81
GC	424 (.044)	1.05
GA	575 (.059)	1.01
GG	478 (.049)	1.21

Note.—Data are for the hypothesis that the dinucleotide frequency is the product of the two respective nucleotide frequencies.

These results indicate that the infinite-sites mutation model is inappropriate for the LPL locus, and, in light of the literature reviewed in the Introduction, it may be inappropriate for human nuclear DNA in general. This conclusion is relevant to resolution of the discrepancies noted earlier between the current analysis of recombination and those based on the Hudson and Kaplan (1985) and Hudson (1987) estimators. The CT method is not based on the infinite-sites assumption. As a consequence, and as shown by the results of the mtDNA analysis, this technique is not sensitive to violations of the infinite-sites model, whereas the methods of Hudson and Kaplan (1985), Hudson (1987), and Hey and Wakely (1997) demonstrate extreme sensitivity.

Implications for the Use of SNPs to Detect Disease Genes through Linkage Disequilibrium

The current analysis reinforces the conclusion by Clark et al. (1998)—that the use of a few randomly chosen SNP markers within 10 kb of the LPL gene would not be a reliable method of detection of nearby causal variation through disequilibrium. First, because of the recombinational hotspot, it is unlikely that any single marker would display substantial disequilibrium throughout this region, which itself represents only a third of the coding portion of this locus. An SNP is only likely to be in disequilibrium with either the 5′ or 3′ end of the region, and any SNP is unlikely to show disequilibrium with mutations within the recombinational hotspot. Consequently, on the basis of the recombinational hotspot alone, it would take several SNPs to provide disequilibrium coverage in just this third of the LPL locus. If a site associated with disease risk were in the region of the recombinational hotspot, it is unlikely that any of the flanking SNPs would be useful in a disequilibrium-based association test.

This difficult situation is made worse by the fact that nearly half of the polymorphic sites are also highly mutable. SNPs, by definition, are polymorphic, and therefore randomly chosen SNPs are highly nonrandom with respect to mutable motifs in the genome. Moreover, the mutagenic mechanisms are such that the same nucleotide state is expected to recur independently. This recurrence of allelic states should break down disequilibrium with other sites, even those displaying little or no recombination with the SNP. Therefore, an SNP at a mutagenic site is an inappropriate choice for marker-association studies. Recombinational and mutational hotspots do not mean that it is impossible to chose a handful of SNPs that would provide disequilibrium coverage of much of the gene, but only that randomly chosen SNPs are not likely to be informative. Once the causes of apparent homoplasy are known, it is possible to choose informative SNPs. In another study, we will present how this may done for the LPL locus.

Overall, our results imply that both recombinational and mutational hotspots have played significant roles in shaping the haplotype variation at the LPL locus. Although these two strong forces for creation of variation make the haplotype patterns complex, the current analysis shows that we can at least partially separate and quantify their effects. Sorting out the roles of mutational accumulation in allelic lineages and of recombination not only allows phenotypic association studies to be performed but also allows inferences about the physical location, in the gene region, of any detected genetic effects on phenotype (e.g., see Keavney et al. 1998). The knowledge that the haplotype variation in LPL has been shaped by a combination of recombinational events and highly mutable sites presents us with the challenge of using this information to optimize tests of genotype-phenotype associations at this locus, a challenge that we will take up in subsequent studies.