The Size Distribution of Homozygous Segments in the Human Genome

Introduction

When we say that an individual is homozygous for a gene, we mean that both copies of the gene are identical in sequence. If one were to obtain DNA sequences flanking such a gene, one might imagine that the homozygosity would continue for some distance in either direction. Theoretically, the lengths of segments of homozygosity will depend, in a complicated way, on the mutation rate, the effective population size, the effect of mutations on reproductive fitness, population subdivision and growth, and the pattern of inbreeding in the population. Sampling of human polymorphisms to date has not been designed to identify the length of such homozygous segments, because it would take either a concerted sequencing effort aimed just at this problem or very dense SNP genotyping to see significantly long segments of homozygosity. In cases in which sequencing from diploid individuals was done, no homozygous blocks larger than 8 kb were found in lipoprotein lipase (Clark et al. 1998) and none larger than 13 kb were found in ACE (Rieder et al. 1999). These cases represent only a small window into the genome, and so they tell us nothing about the size of the largest homozygous segment along an entire chromosome. Empirical determination of the distribution of sizes of these blocks of homozygosity in the human genome had to await the development of sufficient numbers of polymorphic markers and the will to test large numbers of such markers in individuals.

In this issue, Broman and Weber (1999) have done an analysis of an array of 8,000 STRPs in the CEPH families, and their remarkable finding is that several families have average largest homozygous segments of >10 cM, even among “outbred” individuals (from Utah and Venezuela). The identification of homozygous segments from STRP data involved a few technical hurdles that had to be surmounted. There is a low level of typing error that must be modeled and accounted for, and Broman and Weber do so with a likelihood approach. STRPs also have the nasty habit of back mutation, so a recombined block may appear to have been unrecombined if an STRP allele mutated back. Given the density of markers used, recombination events are likely to cause blocks of several STRP differences to be exchanged. Gene-conversion events may make exchanges of single microsatellite loci and may thus be difficult to distinguish from typing errors. Broman and Weber use a reasonable heuristic approach to controlling these confounding effects, and, even if one ignores such smaller exchanges, large blocks of homozygosity are clearly evident. The challenge is to determine whether we should be surprised at the finding of runs of homozygosity >10 cM in length in outbred human populations.

Modeling a Single Genomic Segment

Before formulating a model for homozygous segments, we must first distinguish between several kinds of identity that may be observed across a region. An “unrecombined autozygous segment” is one that has been passed without recombination from a common ancestor along two lineages and into the observed individual. An “autozygous segment” is a run of DNA that has passed along two lineages from a common ancestor but may have recombined apart and back together again. A “homozygous segment” is a run of DNA in which every site in the two homologous chromosome copies is identical. Note that a homozygous segment may be, but is not necessarily, an autozygous segment, because two quite remote copies of part of the gene may be identical after multiple mutation and recombination events. Finally, “apparent homozygous segments” are actually different but appear to be identical because of scoring errors. The empirical data tell us about homozygous segments, but it is much easier to model unrecombined autozygous segments, so, for now, we will restrict our attention to this case.

Let's follow the segment surrounding one particular gene and model the occurrence of flanking recombination events. Imagine that each time recombination occurs, the exchange is with a chromosome drawn from the population that is not identical by descent to the initial chromosome. Further imagine that the only way that the two copies of the gene can be identical by descent is for both to arrive unrecombined in the observed individual. That is to say, we will initially assume there is exactly one path of coancestry. This assumption is certainly violated in reality, but bear with it for the moment.

A recombination event anywhere along the path of coancestry will terminate the autozygous segment. We can model the size of unrecombined segments by focusing on one autozygous segment and specify the probabilities of recombination events as we move along the chromosome. If recombination events occur independently (zero linkage interference), the probability of recombination will be constant as we move along the chromosome. The distribution of intervals between recombination events would then be exponential: F(x) = 1 − e^−λx, where λ is a rate parameter. In this case, the number of recombination events along a chromosome of length t will be Poisson: Pr{N(t)=k} = 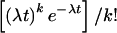. This defines a Poisson renewal process, which allows us to calculate many features of the size distribution of unrecombined segments (Karlin and Taylor 1975). It is clear that the longer the time back to the common ancestor, the more recombination events will have occurred and the smaller the unrecombined segments will be.

To find the largest unrecombined segment given that the chromosome has been broken into r segments, imagine dropping the r−1 recombination events along a unit-length line. If we identify a particular segment that is autozygous, and if we can count the number of meioses that have occurred since the common ancestor of the middle of this segment, then the expected size of the autozygous region is

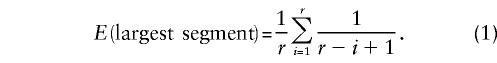This formula was first derived for a model called, somewhat whimsically, the “broken stick” model for relative species abundances (MacArthur 1957). It is straightforward to simulate the process of distributing recombination events along a chromosome, and the correspondence between equation 1 and the simulations is quite good (table 1 and fig. 1A). One might think that this process would give a very dispersed distribution, but figure 1B shows that the largest unrecombined segment is fairly tightly dispersed. Although this is a grossly oversimplified model, we can get some useful insights from it. When Broman and Weber (1999) find that individuals in family 884 had homozygous segments averaging 11 cM, we can see that this means the chromosomes in which those segments were found faced 35–40 recombination events in the lineages back to the common ancestor.

Table 1.

Mean and Maximum Size of Autozygous Segments for a Range of Intervening Recombination Events on a Single, 100-cM Chromosome

	Segment Size (cM)
No. of Recombinations	Meana	Maximuma	Expected Maximumb
5	16.67	40.90	40.83
10	9.09	26.21	27.45
15	6.25	20.96	21.13
20	4.76	16.92	17.36
25	3.85	14.49	14.82
30	3.23	12.77	12.99
35	2.78	11.24	11.60
40	2.44	10.31	10.49
45	2.17	9.64	9.60
50	1.96	8.84	8.86

^aFrom 1,000 simulations.

^bFrom equation 1.

Figure 1.

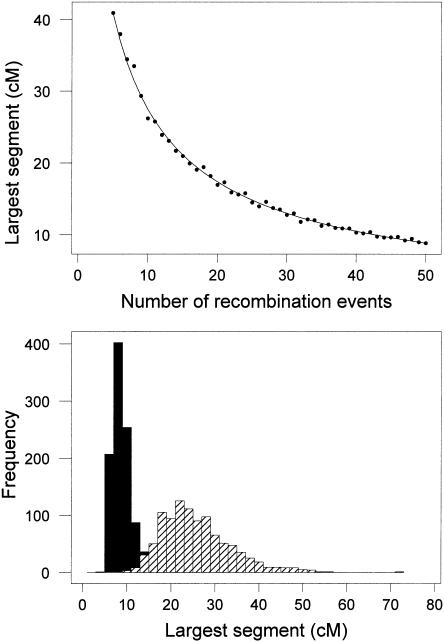
A, Decline in size of unrecombined segments with increasing numbers of recombination events. The solid line is from the theoretical prediction (eq. 1), and the dots are from 1000 replicates of dropping recombination events on a unit line (length 100 cM). B, Distribution of lengths of unrecombined segments for 10 recombination events (hatched bars) and for 50 recombination events (solid bars).

Coalescence Models

The model and simulation presented above both lack complications that are encountered in real populations. We assumed that each individual has only one path of coancestry, whereas actual individuals will have thousands of paths of coancestry if one looks back far enough. Furthermore, the set of paths of coancestry will be radically different from one chromosomal location to another. Finally, two adjacent segments can be completely homozygous but have different ancestral histories, if recombination breaks them apart and later patches them back together. These complications must be built into any model that attempts to explain observations like those of Broman and Weber (1999). Fortunately, there is a rich history of work on this problem in theoretical population genetics, and a brief review is in order.

Kingman (1982) first developed the coalescence model, wherein the genealogical relationships among unrecombining alleles sampled from an equilibrium population were described. The basic idea was to consider an extant sample of k alleles from a population and to model the distribution of times back to “coalescence” of some pair of alleles into an ancestral allele, at which point there would be k−1 alleles. This recursive process continues back in time until there is a single ancestral allele. In a chromosome with recombination, each unrecombined segment follows this coalescent formulation, so Hudson (1983) considered the case with recombination by keeping track of the recombination events that broke up the coalescence into such segments. Hudson and Kaplan (1985) showed that this theory could be used to estimate numbers of recombination events on the basis of sample data from extant populations.

An elegant formulation of the problem, known as an “ancestral recombination graph” (Griffiths and Marjoram 1996, 1997), allowed the calculation of distributions of times of common ancestry on the basis of the full configuration of mutations observed in sampled alleles. The ancestral recombination graph traces the history of sampled sequences back in time, merging two alleles when coalescence events occur (as above), but splitting the lineage into two when recombination events occur. Wiuf and Hein (1997) derived expressions for the number of ancestral sequences on such a graph and showed that it can become much larger than the sample size, as a result of recombination, but also that, even with recombination, the process must end by coalescing to a single ancestral allele. Wiuf and Hein (1999a, 1999b) derived results that are most relevant to the present problem, obtaining expressions for the number of adjacent nucleotides that share the same common ancestor. We might also want to know the distribution of times back to a common ancestor for different regions of a chromosome, on the basis of data like that of Broman and Weber (1999), and the computational load for obtaining these estimates was recently reduced by applying a Monte Carlo Markov chain (Griffiths 1999). Finally, Metropolis-Hastings sampling has been shown to be very effective for obtaining parameter estimates in coalescence models (Kuhner et al. 1998; Beerli and Felsenstein 1999) and is being applied to intragenic recombination as well (Felsenstein et al. 1999). Although these methods do not explicitly consider segments of homozygosity, one gets the needed estimates simply by considering properties of common ancestry of segments drawn as pairs from the population.

Consideration of sizes of shared chromosomal segments flanking a particular mutation has emerged as an important problem relevant to linkage disequilibrium mapping, and recent progress has been reported on this problem as well (Donnelly and Wiuf 1999; McPeek and Strahs 1999).

All the above models have assumed random mating, and the possibility for consanguinity in human populations needs to be considered. Recently, Nordborg (1999) showed that partial selfing can be accounted for in coalescence models with recombination by scaling the parameters for the population size and rate of recombination, and this approach should work for other forms of inbreeding as well.

Further Refinements and Applications

In the field of population genetics, there is a rich history of advancements made by noting discrepancies between models and theory. If observed segments of autozygosity differ in size from model predictions, we can begin to identify several possible reasons. First, natural selection will remove from the population those individuals who are autozygous for very deleterious alleles, leaving a smaller-than-expected block size. We do not tend to keep track of consanguinity if the potential common ancestor is more than four or so generations back, but having common ancestors five, 10, or even 20 generations ago is far from being “outbred” in the context of tracking homozygous segments in entire genomes. Very large segments can remain intact for long periods (fig. 1a). There will be large sampling problems to face, and the identification of homozygous blocks will depend on marker density and heterozygosity, as Broman and Weber (1999 [in this issue]) illustrate. Population growth will also distort the distribution of times back to common ancestry (Bertorelle and Slatkin 1995), and this may be especially evident in distributions of homozygous segments. Regions of the genome with low levels of recombination per megabase are expected to have larger segments of homozygosity. Observation of unexpectedly large homozygous blocks may also have a genetic cause, such as uniparental disomy (Smith et al. 1994; Martin et al. 1999; Uehara et al. 1999). Our ascertainment for uniparental disomy is through clinical cases, and, if some uniparental disomy for some chromosomes is asymptomatic, this phenomenon may well be more common than currently thought.

Coalescence approaches will allow us to take the exciting step of turning these problems around, making inferences, and estimating population parameters from observed distributions of homozygous segment lengths. Although classical population-genetics theory tells us that one can have the same net inbreeding coefficient either with one short path of common ancestry or with several longer paths, the consequences will be very different for the distribution of blocks of homozygosity. The complete genome sequence of an individual will give the complete distribution of homozygous segments, and this distribution will allow unprecedented resolution for inferences about the number and depth of common ancestors. Many interesting inferential challenges will arise when we consider the population genetics of whole genomes.