On a Randomization Procedure

To the Editor:

Zhao et al. recently (1999) proposed a novel way of determining the statistical significance of a given test statistic in the context of allele-sharing methods. The procedure promises to be applicable to any pedigree structure and to both qualitative and quantitative traits and is based on a randomization approach. The classical randomization test, as introduced by Fisher (1935), has proved to be a widely applicable and powerful tool for geneticists and scientists in general. It requires fewer assumptions than many other standard tests and has appealing small-sample properties, as the P values it produces can be claimed to be “exact.” As flexible as the classical randomization procedure is, its validity depends crucially on certain symmetry/exchangeability conditions. For example, in a case/control study, a “case” and a “control” are exchangeable under the null hypothesis. Close inspection reveals that the method of Zhao et al., which generates a distribution of the NPL score (Kruglyak et al. 1996) by randomization of the conditional probabilities of different inheritance vectors in a specific way, does not, in general, satisfy such exchangeability conditions. As a consequence, it cannot be assumed automatically that this procedure will share the appealing properties of the classical randomization test. Indeed, as demonstrated below, not only can P values that are computed with a small sample be very misleading, but the results for large samples can be off systematically as well. For example, for affected full-sib pairs with missing data on the parents—a common design for late-onset diseases—the method underestimates the variance of the NPL score by a factor of 2 asymptotically, an effect that corresponds to inflating a Z_stat (a test statistic that has, asymptotically, a standard normal distribution) by a factor of .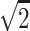

We start by reviewing how the randomization procedure works with the family structure of two parents and two affected sibs and the scoring function S_pairs. In theory, the inheritance vector has four “bits,” one paternal bit and one maternal bit for each of the two sibs. For example, the paternal bit of the first sib indicates whether the allele he or she inherited from the father originates from the paternal grandfather or the paternal grandmother. However, with no data on the grandparents, there can be no information on an individual bit. The information is on whether the paternal bits of the two sibs are the same, which corresponds to whether the two sibs have the paternal allele IBD (identical by descent), and on the same information with the maternal bits. Hence, to understand/describe what the randomization procedure is doing, one can focus on a reduced vector with two bits, one paternal sharing bit (one for IBD sharing, zero for not sharing) and one maternal sharing bit. This sharing inheritance vector has four possible states: (0,0) corresponds to the two sibs sharing zero alleles IBD, (1,1) corresponds to sharing both alleles IBD, (1,0) corresponds to IBD sharing of the paternal allele but not of the maternal allele, and (0,1) corresponds to not sharing the paternal allele but sharing the maternal allele. If the sharing vector can be determined without uncertainty, then (1,1) gives an NPL score of 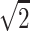, (0,0) gives an NPL score of 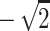, and both (1,0) and (0,1) give an NPL score of 0. In general, with incomplete information, the NPL score for the pair is defined as

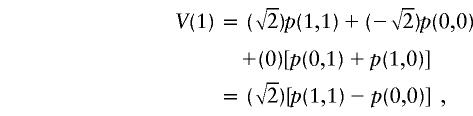where p(·,·) are the conditional probabilities of the various configurations of the sharing vector, given the marker data. Apart from the actual NPL score V(1), three other hypothetical NPL scores are generated by the randomization procedure by flipping one or both bits:

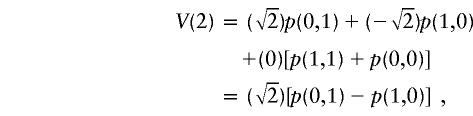obtained by flipping the paternal sharing bit;

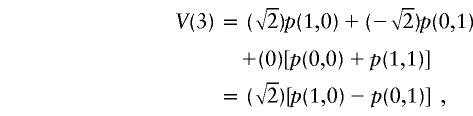obtained by flipping the maternal sharing bit; and

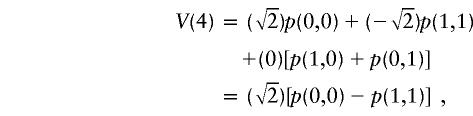obtained by flipping both sharing bits. Note that V(4)=-V(1) and V(3)=-V(2). The four values are given equal probabilities by the procedure when it is applied to generate a randomization distribution.

Here, consider the case in which there are no genotype data on the parents of the affected sibs. In this case, it is obvious that the data cannot distinguish (0,1) from (1,0), hence p(0,1)=p(1,0) and V(2)=V(3)=0, a result that has serious consequences. Suppose the data consist of n affected sib pairs with no genotype data on the parents. For i=1,…,n, let W_i be the NPL score for sib pair i, so that the overall NPL score is

Let w_i be the observed value of W_i, and define X_i,i=1,…,n, as independent random variables with discrete distributions P(X_i=w_i)=1/4,P(X_i=-w_i)=1/4, and P(X_i=0)=1/2, and

The P value determined by the randomization procedure is P(X⩾w), where w is the observed value of W. As a small-sample example, consider n=10 and the only genotype data is a single biallelic marker with alleles A and a. Let p and q=1-p be respectively the population frequencies of A and a. Suppose for each of the 10 sib pairs, the two sibs have two alleles identical by state (IBS). In this case, w_i is positive for all 10 pairs, and it is easily seen that the randomization P value is

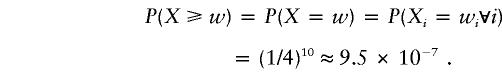This value is obviously too small, since it is the right P value when the results are IBD instead of IBS; it is also suspicious that this value does not depend on the allele frequencies p and q. Indeed, the probability that all 10 sib pairs have two alleles IBS within pairs is

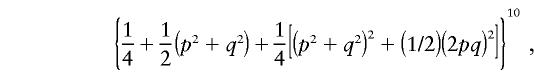which is equal to .0054, .0067, .0127, .0366, and .1592, respectively, for p=.5, .6, .7, .8, and .9. Obviously, the values of w_i depend on the allele frequencies. However, in this example, because the values of w_i are all positive, the randomization P value is not sensitive to their absolute values. Hence, this can only be considered as a small-sample example, since, with large-sample examples, some values of w_i will be negative and the allele frequencies will have an effect on the answer. For the large-sample behavior of the randomization procedure, note that X_i has mean 0 and variance w²_i/2, and so X has mean 0 and variance 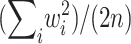. It follows that the distribution of 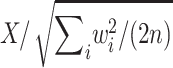can be approximated by a standard normal distribution, and the randomization P value,

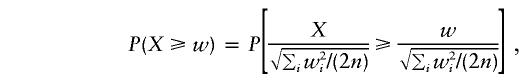can be approximated by

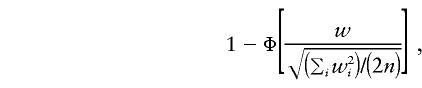where Φ(·) denotes the cumulative distribution of the standard normal. In other words, asymptotically, the randomization procedure corresponds to a method that treats

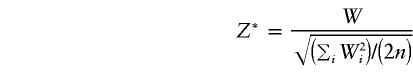as a statistic that has a standard normal distribution under the null hypothesis. However, under the null hypothesis, E(W_i)=0 and Var(W_i)=E(W²_i). Asymptotically (n→∞),

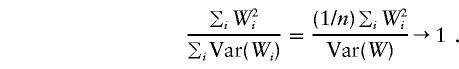with probability 1, and

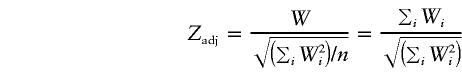has, asymptotically, a standard normal distribution under the null hypothesis. A discussion concerning Z_adj and other test statistics that are asymptotically valid can be found in Teng and Siegmund (1998) and Nicolae et al. (1998). The key here, however, is to note that

So when Z_adj=2, which gives a P value of 1-Φ(2)=0.023, the randomization procedure will give a P value that is approximately 1-Φ(2.83)=0.0023.

Recall that the large-sample behavior of the randomization procedure presented above is based on the case of affected sib pairs with no data on the parents. In general, the large-sample behavior of the procedure depends on both the family structure and the missing data patterns. For example, it can be shown that, for affected half sibs, the randomization procedure is calibrated for large samples and is asymptotically similar to using Z_adj. Although, as demonstrated, the procedure is anticonservative for sib pairs with no data on parents, it can be shown that—at least for the single-marker case—it is asymptotically slightly conservative for sib-pair data with genotypes on both parents. Real data sets tend to have a mixture of family structures and missing data patterns, and, hence, there is no simple way to make adjustments. Zhao et al. (1999) found that their randomization procedure gives smaller P values than the likelihood methods of Kong and Cox (1997) in most of the examples they looked at. Since the likelihood methods are asymptotically efficient, given a specific model, and are asymptotically equivalent to other methods that are efficient (Cox and Hinkley 1974), this suggests that the randomization procedure might be anticonservative in many of the examples.

To gain some understanding of why this randomization procedure does not, in general, give exact P values, it may help to consider the special situation where it does. Suppose we have sib-pair data and are always able to determine the sharing vector with no uncertainty. This means that for a pair, given the data, one of p(1,1), p(0,1), p(1,0) and p(0,0) is equal to 1. One can see that the four values V(1), V(2), V(3), and V(4) will always be some permutation of 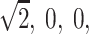and . 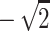Hence, the four values of V always correspond to the four possible values of the NPL score. In addition to the values, the randomized distribution generated is exactly the same as the distribution of the NPL score under the null hypothesis. In general, with complete descent information, the randomization procedure gives valid exact P values that are the same as those obtained by direct simulation and the “exact P values” of GENEHUNTER (Kruglyak et al. 1996). This might have been the scenario which stimulated the development of the procedure. For comparison, consider the classical randomization procedure in a matched-pairs study. Within a pair, the procedure permutes the responses of the case and the control. The idea is that if we are given the two response values of the case and the control, but not the correspondence between the subjects and the responses, then the two permutations have the same probability under the null hypothesis. Hence, the classical randomization test can be considered as a conditional test that conditions on the observed response values without the correspondences. The randomization distribution of Zhao et al., in general, cannot be interpreted as any conditional or unconditional distributions of the outcome. Indeed, consider sib pairs with no data on the parents. If the two sibs have 0 alleles IBS, then p(0,0)=1, 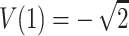, and the hypothetical value 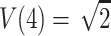. But 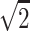is not even a possible outcome, since, with no data on the parents, the NPL score generally will be positive but smaller than 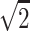, even if the two sibs have two alleles IBS. So, one way to understand why the randomization procedure here does not give exact P values is that, although the different configurations of the inheritance vector have some obvious exchangeability properties for complete information, the same symmetry does not hold for every missing data pattern. It is unfortunate that this lack of symmetry affects not only the small-sample properties, but also the large-sample behavior.