Simple model for tuberculosis in cattle and badgers

Abstract

As an aid to the study of bovine tuberculosis (TB), a simple model has been developed of an epidemic involving two species, cattle and badgers. Each species may infect the other. The proportion of animals affected is assumed relatively small so that the usual nonlinear aspects of epidemic theory are avoided. The model is used to study the long-run and transient effect on cattle of culling badgers and the effect of a period without routine testing for TB, such as occurred during the 2001 epidemic of foot-and-mouth disease in Great Britain. Finally, by examining the changes in cattle TB over the last 15 years, and with some other working assumptions, it is estimated that the net reproduction number of the epidemic is ≈1.1. The implications for controlling the disease are discussed.

Mathematical modeling of infectious disease, especially in humans, has a long history (1). Two very different kinds of dynamical model are simple outline and quasirealistic models. The former aim to capture the essence of a complex situation in a few key aspects and then to use these to explain the qualitative patterns of behavior to be expected and even to give semiquantitative predictions. Quasirealistic models, by contrast, aim to get much closer to reality by representing, almost inevitably in a model implemented by computer rather than by mathematical analysis, as many features of reality as is feasible. Despite the attractions of greater realism, a common problem with such models is the need to specify the values of a considerable number of forms of dependence and the numerical values of unknown parameters, often, as in the present instance, aspects about which little is known. The consequent need for extensive and systematic sensitivity analyses may undermine the usefulness of such models and mean that such data as are available are consistent with many different interpretations.

In the present work we consider a deterministic multispecies transmission model of the former simpler type to describe Mycobacterium bovis infection in cattle and badgers. After setting out a fairly general model framework allowing both within- and between-species transmission, we look at a number of special situations corresponding in particular to interventions on one or other species.

General Model Specification

We consider a reasonably homogeneous area such that at time t there are X₁(t) = C(t) infected cattle per km² and X₂(t) = B(t) infected badgers per km². We suppose that the proportions of infected animals are relatively small, say <0.2, so that the nonlinear effects characteristic of epidemic theory, because of the depletion of the pool of susceptible animals, are not important. This assumption seems reasonable because reports of more than a small number of reactor cattle within individual herd breakdowns are rare. Also, we do not distinguish between infected and infectious animals, thus making the approximation that all infected animals of a particular species are equally infectious.

A major assumption is that of spatial homogeneity over the area considered. This assumption means, in particular, that use of the conclusions at a very local level would not be justified.

Let a_ij be the rate per unit time (usually a year) at which one animal of species j infects animals of species i. Let animals of species i be removed at a total rate r_i and suppose that restocking introduces new infected animals at rate s_i. Note that the removal rate of cattle at time t, r₁(t), includes both routine slaughter and slaughter after identification of disease. We assume that although both removal and immigration rates may be affected by policy decisions or external conditions, they are constant over defined periods.

Let A denote the matrix of the a_ij and X(t) = {X₁(t), X₂(t)}^T. Further, let R = diag(r₁, r₂) and S = {s₁, s₂}^T. Then

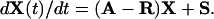[1]

Therefore, if B = R – A, and if initially X(0) = X₀, then we have that

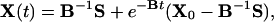where the matrix exponential is computed through the spectral decomposition B = HΛH^–1 with Λ = diag(λ₁, λ₂). Then

Note that this discussion could be applied formally to any number of species. Furthermore, four “species” could be used to represent cattle and badgers in two geographical regions. This metapopulation approach will not be explored here.

If, on the other hand, the number of infected badgers B(t) at time t were externally influenced, for example by culling (whether one-off or repeated), rather than determined by Eq. 1, the resulting equation for C(t) is

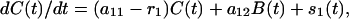where it is convenient to allow also that the restocking rate may vary over time.

Epidemiological Setting

Cattle herds are subject to regulations set out in the Animal Health Act requiring regular tuberculosis (TB) tests. Each herd is subjected to a parish-based testing interval of between 4 yr and 1 yr, where parishes with the lowest incidence are assigned 4-yearly testing and parishes with the highest incidence are assigned annual testing. Routine whole-herd tests are carried out in accordance with the parish test interval, and additional tests can be conducted at any time, for example, in response to slaughterhouse checks or TB in neighboring herds. A herd is said to experience a TB “breakdown” if one or more members of a cattle herd fail the conventional TB skin test or show evidence of TB lesions at slaughterhouse inspection.

In 2003, ≈58,000 herd tests (comprising >4.5 million cattle tests) were performed in Great Britain, disclosing 3,219 new herd breakdowns, just over half of which were subsequently confirmed (2). As a result of these tests some 20,000 reactor cattle, and ≈3,000 contacts, were identified and compulsorily slaughtered, giving an average of 3.7 reactor cattle slaughtered per breakdown (counting all breakdowns, new and ongoing, recorded in 2003). For comparison, there were ≈9 million cattle and calves in Great Britain at the time.

Badgers were first linked to cattle TB in the UK in 1971 when M. bovis was isolated in a badger carcass. In response, badger culling was undertaken in places where TB occurred, and in the past 30 yr the culling strategies have changed several times (3, 4). Initially farmers were licensed to cull badgers. From 1975–1981, badgers were gassed in their setts by Ministry of Agriculture, Fisheries and Food staff. This approach was replaced by cage trapping, initially based on the “clean ring” strategy, designed to identify and remove clusters of infected badgers. From 1986 culling was more limited in scope and took place only on land used by cattle in which M. bovis was isolated. This form of culling was intended solely as an “interim strategy” pending development of a more selective culling policy (5) but continued until 1997 when a major review of TB control was undertaken (3).

Despite a number of reviews (3, 5, 6), the effectiveness of badger-targeted strategies at reducing TB in cattle remains uncertain, in particular because none of the historical badger removal strategies was accompanied for comparison by a control strategy of no culling. Following a recommendation of the Krebs report (3), the Independent Scientific Group on Cattle TB was set up and charged with designing and overseeing a large-scale field trial aimed at evaluating two different approaches to badger culling as a means of reducing TB incidence in cattle (7–10).

Parameters

For ease of interpretation, conclusions are mostly expressed in terms of dimensionless parameters. In some cases, for example the cross-infection rates, there is little or no information to indicate what values are plausible. In others, plausible approximate values can be given.

The removal rate for cattle depends on the average life of cattle in the system when infection is not detected, the cattle testing interval, and the sensitivity, p, of the skin test for TB. With routine testing every d years, there are a number of possible assumptions about repeat tests. One extreme is that a herd breakdown not detected in one year will certainly be detected in the next test. Another extreme is that the infected cattle not detected on one occasion will not be detected at the next test either. An intermediate assumption, and the one made here, is that the same sensitivity applies each time. It then follows, assuming infection starts at a random time between tests, that the average interval between incidence and detection is

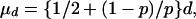[2]

where the second term on the right-hand side arises from the geometric distribution of the number of retests needed. In fact the testing after a suspect case follows a complicated set of rules, which we do not attempt to model; probably Eq. 2 overestimates μ_d.

From Eq. 2, the average time between infection and detection is d/2 if the test is perfect. Diagnostic test insensitivity in effect increases the effective testing interval by a factor equal to μ_d/(d/2) = 1 + 2(1 – p)/p. For example, with sensitivity p = 2/3, the ratio is equal to 2, so one-year testing is equivalent to 2-year testing with a perfectly sensitive test (see Table 1).

Table 1. Ratio of effective to nominal testing interval induced by test sensitivity p.

p	0.50	0.60	0.70	0.80	0.90	0.95	1
Ratio	3.00	2.33	1.86	1.50	1.22	1.11	1.00

We base our estimate of μ_n, the mean time in the herd in the absence of a detected breakdown, on the distribution of life in the disease-free herd. Suppose that this quantity has probability density f(x) and cumulative distribution function F(x) with mean and coefficient of variation μ_f and CV_f. Then, if infection occurs randomly at a low rate independently of age, the probability density of time between infection and routine removal in the absence of testing is the equilibrium recurrence time distribution (11)

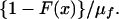Thus, the mean time between infection and routine removal is

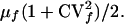Finally, the removal rate of infected cattle is approximately

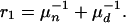[3]

We take the distribution of the age of cattle on routine slaughter as applying to infected cattle that have not been detected, leading to μ_n ≈ 3 yr.

Equilibrium Theory

As the first of the special situations, suppose that the system is in equilibrium so that the input of new infected animals just replaces egress. The first component equation for the equilibrium values X₀ = (C₀, B₀), shows that

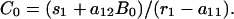[4]

There are two immediate consequences from this equation. First, an equilibrium is possible if and only if r₁ > a₁₁, in practice if r₁ is appreciably greater than a₁₁. With annual testing we estimate that r₁ is between 1.3 (if test sensitivity is 66.7%) and 1.7 (if test sensitivity is 80%). That is, the number of cattle infected per year by one infected bovine, a₁₁, must be appreciably less than 1.3. Note that if this situation was not the case, one would expect appreciable numbers of herd breakdowns with a considerable number of reactor cattle. Second, the equilibrium level is inversely proportional to (r₁ – a₁₁) and r₁ is determined by testing interval d and test sensitivity p.

Now suppose that the badger population is reduced to (1 – k)B₀ and held there by repeated culling and that all other aspects of the system, including S, remain unchanged. Suppose further that a new equilibrium for the number of infected cattle is reached. The resulting value of C(t) is

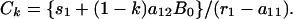Therefore, the proportional reduction in cattle infection is determined from

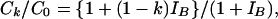[5]

say. Here I_B = a₁₂B₀/s₁ is a measure of the relative influence of badgers as compared with disease in cattle restocked into the system. It is essentially the ratio of the number of cattle infected by badgers per year to the number of infections in cattle brought in from outside the system per year.

Table 2 gives C_k/C₀ (Eq. 5) for a range of values of k and I_B. In this formulation the proportional effect of reducing, or increasing, the badger population depends neither on the removal rate, r₁, nor on the cattle-to-cattle infection rate, a₁₁, within an area, although these do, of course, affect the actual level attained. The level of reduction achieved in the badger population would have to be maintained by repeated culling for these results to apply. The value of I_B is unknown.

Table 2. Ratio C_k/C₀ (Eq. 5) of infected animals to initial level after reducing badger level by factor k as a function of the badger influence ratio I_B.

	IB
k	0.10	0.50	1.00	2.00	5.00	10.00
0.2	0.98	0.93	0.90	0.87	0.83	0.82
0.5	0.95	0.83	0.75	0.67	0.58	0.54
0.8	0.93	0.73	0.60	0.47	0.33	0.27
1	0.91	0.67	0.50	0.33	0.16	0.09

In this discussion it is assumed that only the number of infected badgers is changed. If, at the other extreme, the external incidence rate s₁ also were reduced by the same factor k then the equilibrium level is reduced by that factor, too, assuming removal rate and cattle-to-cattle transmission within the area remained unchanged.

Time-Dependent Effect of Initial Culling: A Single Cull

To study the rate at which the equilibrium levels in the previous discussion are achieved and to examine some other perturbations of the system, we solve the original differential Eq. 1 in the form

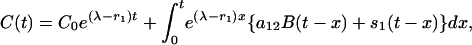where C₀ is the initial value of C(t).

We examine a number of different situations. First, as in the previous section, suppose that at t = 0 the system is in equilibrium corresponding to B(t) = B₀ for t < 0, so that C₀ is given by Eq. 4 and that the number of infected badgers is instantaneously reduced to (1 – k)B₀ and thereafter returns to its initial level, the return being represented for t ≥ 0 by

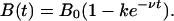Thus, after time 0.69/ν, the badger population will have returned halfway to its original level, B₀. The possibility of maintaining the badger population permanently at its new level is represented by ν = 0.

The general solution now takes the form

Thus,

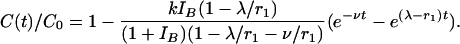[6]

The function C(t) reaches a minimum after time

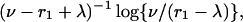and then returns toward its initial value C₀. If the two timescales determined by cattle aspects, r₁ – λ, and by badger aspects ν are very different, the more rapid timescale dominates behavior.

This equation specifies prevalence as a function of time. In some ways, incidence, that is the rate of occurrence of new infections, although not directly observable, is more relevant, and this rate is

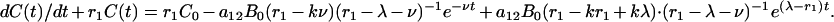When divided by the equilibrium rate r₁C₀ this value is

[7]

Thus, immediately after the reduction in the number of badgers, the rate of new infections is reduced from r₁C₀ by the factor

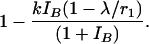Time-Dependent Solution: A Maintained Cull

Next suppose that at time t = 0 the testing frequency is changed from every d years to every d′ years so that the removal rate changes from r₁ to r′₁, B₀ and s₁ remaining unchanged. Then from Eq. 4

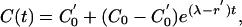where C′₀ is the equilibrium level of C(t) at the new testing frequency. In fact

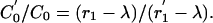[8]

Equilibrium requires that the removal rates exceed λ and if that state were reached, Eq. 8 shows that the equilibrium level of prevalence achieved would be approximately inversely proportional to the removal rate.

Time-Dependent Solution: Interruption of Operations

Finally, suppose that, starting from equilibrium, there is a period (0, t₀) in which there is no removal or restocking, but infection by badgers and by cattle-to-cattle transmission in the area continues. Then, after time t₀ the number of infected animals is given by the solution of the full set of equations and is

[9]

Suppose then that normal testing and restocking resumed. Then after a further time t

[10]

Therefore,

[11]

If λt₀ is small, this ratio is approximately

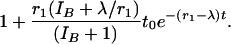This situation corresponds to the restriction of livestock movements between farms and the suspension of routine tuberculin skin testing of cattle during the foot-and-mouth disease epidemic in the United Kingdom in 2001.

Conditions for Epidemic Progression

So far, much of the discussion has centered around the notion of a system in equilibrium and suffering relatively minor deviations from that equilibrium. The condition for epidemic growth, essentially that the net reproduction rate exceeds one, is that the matrix B = R – A have at least one negative eigenvalue. This negative eigenvalue would imply an exponential increase in prevalence in both species, although of course the effect might be numerically small in one of the species.

Numerical Results Based on Model

The results sketched above depend on a limited number of unknown parameters. One of the functions of simple models such as this one is in fact to highlight the features of the system most likely to have a big impact on the outcome. An example is the index I_B influencing the outcome of a permanent reduction in the number of infected badgers, and another is k, the efficiency of culling. As has already been mentioned, the amount of information available about all of the parameters is limited, and study of a range of parameter values is thus essential. We can, however, obtain approximate relevant ranges by the following arguments.

To set out the numerical results, it is helpful to use dimensionless units, although for substantive interpretation it is usually necessary to convert back to natural units. Thus, we set r₁t = τ so that τ is a dimensionless timescale determined by the replacement rate r₁. Further, we define l = λ/r₁ and ν = ν/r₁, thereby expressing the cattle-to-cattle transmission rate and the badger return rate relative to r₁.

First, for the most part we assume λ is small compared with r₁, i.e., that λ is small. Were λ not small, most outbreaks in a farm would be multiple and often involve whole herd breakdowns. These are, however, relatively rare.

For interpreting τ in natural time units, typically years, we have to estimate r₁. We take a diagnostic test sensitivity of p = 2/3, this value corresponding broadly to reports in the literature (12, 13) to obtain the effective removal rate as r = 1.3 yr^–1. Lower sensitivity would imply decreased r₁, and it is clear from Eq. 4 and other formulas that this change could substantially increase C(t). If the badger population returns to its equilibrium level at a rate of ≈20% per year, then ν = 0.23 yr^–1. For most purposes, therefore, we show functions of time as functions of τ at a range of values of I_B and the culling fraction k.

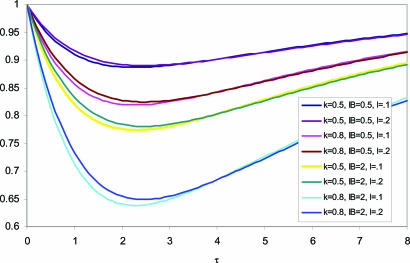
The effect of culling on the equilibrium level of TB is shown in simple form in Table 2. The corresponding standardized prevalence and incidence curves are shown in Figs. 1 and 2 as functions of dimensionless time τ for selected values of I_B, k, and l = λ/r₁. The badger return rate ν = ν/r₁ has been fixed at 0.17. In the standardized time measure τ, a unit of time corresponds to ≈0.75 yr, i.e., τ = 4 translates to 3 yr.

Fig. 1.

The standardized prevalence of TB in cattle (Eq. 6) as a function of time, τ, since culling; the proportion by which the badger population was reduced, k; the relative cattle-to-cattle transmission rate, l; and a measure of the relative influence of badgers as compared with disease in cattle restocked into the system, I_B.

Fig. 2.

The standardized incidence of TB in cattle herds (Eq. 7) as a function of time, τ, since culling; the proportion by which the badger population was reduced, k; the relative cattle-to-cattle transmission rate, l; and a measure of the relative influence of badgers as compared with disease in cattle restocked into the system, I_B.

Both prevalence and incidence fall rapidly after culling to a level determined largely by the efficiency of culling, k, and by the index of badger activity, I_B. They then return slowly to their initial level. This result implies that repeat culling at intervals of perhaps five dimensionless units should hold prevalence close to its minimum level. Clearly a more refined calculation of the effects of repeat culling would be possible.

Eqs. 9–11 were considered to assess the effect of a 9-month cessation of testing during the British foot-and-mouth disease epidemic. In particular, Eq. 11 shows the relative prevalence after resumption of normal procedures. Fig. 3 shows this quantity as a function of time for selected values of I_B and l = λ/r₁. For the range of values considered an initial increase in prevalence by a factor of up to 2 is to be expected followed by a relatively rapid decrease back to the equilibrium level.

Fig. 3.

The standardized prevalence of TB in cattle herds (Eq. 11) after a 9-month cessation of testing and restocking as a function of time, τ, since resumption of skin testing and restocking of cattle; the relative cattle-to-cattle transmission rate, l; and a measure of the relative influence of badgers as compared with disease in cattle restocked into the system, I_B.

Estimation of the Basic Reproductive Number

Consider the growth of the epidemic in cattle over a reasonably large and homogeneous region. Let C(t) be the number of infected cattle at time t. Suppose that they are removed by detection and routine removal at rate r₁ per year. With annual testing at 2/3 test sensitivity and “usual” demographic properties, r₁ is ≈1.3 yr^–1.

Assume that the proportion of animals affected is low and that there is a new infection rate of λ per year per infected animal. Note that these new infections arise from cattle-to-cattle transmission within a herd and by infection by cattle brought in from a source with about the same infection rate. In addition, suppose that there is infection at rate β(t) from an external source, which here we will take to be wildlife.

We then have the differential equation

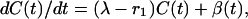[12]

with solution

There is now the difficulty that little is known about the external infection rate β(t). We examine two possibilities. One is to suppose that β(t) is constant, equal to β, say. Then

[13]

and the growth is superexponential.

The second possibility, at least consistent with the general model of Eq. 12, is to suppose that β(t) = γe^(λ–r1)t, i.e., that the epidemic in wildlife roughly parallels that in cattle. Then

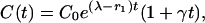[14]

which also is superexponential, suggesting that empirical discrimination between the two forms may be difficult.

If effective estimates can be obtained of (λ – r₁) and either β or γ, the following tentative implications can be made:

• the net reproduction number is λ/r₁;

• the effect on the epidemic of changes in r₁, for example more frequent and/or more sensitive testing, can be drawn;

• the fractional reduction in λ needed to influence the epidemic can be assessed; and

• λ/(λ + β) is the proportion of the epidemic that is internally rather than externally driven.

Eqs. 13 and 14 were fitted separately to TB incidence data (based on the numbers of new herd incidents, both confirmed and unconfirmed) from 1986 to 2000 from England and Wales as a whole, from the Western Region (Cornwall, Devon, Dorset, Gloucestershire, Hereford and Worcester, Avon, Shropshire, Somerset, Isles of Scilly, and Wiltshire), and from the rest of Great Britain (i.e., not in the Western Region). Both models fitted very well, as would be anticipated given the relatively small number of years of data available and the availability of three adjustable parameters. See Fig. 4.

Fig. 4.

The number of TB herd incidents each year in Great Britain along with the indistinguishable model fits based on Eqs. 13 and 14.

Formal confidence limits for the parameters β and γ are quite wide, but those for the more interesting parameter combination λ – r₁ and the net reproduction number λ/r₁ are narrow. Major uncertainties in these estimates relate more to the highly idealized assumptions underlying the model and in addition to those involved in specifying a value for the removal rate r₁.

The various estimates are summarized in Table 3.

Table 3. Estimates of λ – r₁, β, and γ (in yr^–1) and the net reproduction number λ/r₁ for various regions.

Region	λ - r1	λ/r1	β	γ
Based on Eq. 13
Great Britain	0.125	1.09	8.5	—
Western region	0.150	1.11	0.0	—
Outside the Western region	0.053	1.04	14.1	—
Based on Eq. 14
Great Britain	0.096	1.07	—	0.059
Western region	0.135	1.10	—	0.016
Outside the Western region	0.030	1.02	—	0.177

Because the two simple models fit the data similarly well, we cannot distinguish the relative importance of badger-to-cattle transmission on this basis or determine which set of estimates in Table 3 are to be preferred. Fortunately, however, the estimates of the net reproduction numbers vary little depending on which model was fitted. In all cases the true skin-test sensitivity was assumed to be 66.7% over the period under analysis, and the test frequency was assumed to be annual.

If the true skin-test sensitivity were instead 80%, the estimates are slightly reduced. Thus, for Great Britain as a whole, the net reproduction number is estimated to be 1.07 based on Eq. 13 and 1.06 based on Eq. 14. For the Western Region, the corresponding estimates are 1.09 based on Eq. 13 and 1.08 from Eq. 14. Outside the Western Region, the estimates are lower: 1.03 based on Eq. 13 and 1.02 from Eq. 14. Typical formal 95% confidence ranges are ±0.02, but as noted above this width gives a misleading impression of accuracy.

Another source of uncertainty is the best assumption regarding overall testing frequency in each region given that in fact testing frequency was determined in a parish basis with the highest incidence areas having the most frequent testing. If testing every 2 yr was a better approximation to the testing that took place in the area outside the Western Region, then the estimates of net reproduction rate are increased to 1.06 based on Eq. 13 and 1.04 based on Eq. 14, assuming 66.7% test sensitivity.

For each estimate (which is dependent on the assumed level of test sensitivity and overall testing interval), one can obtain the threshold of sensitivity or testing frequency that must be achieved to drop the net reproduction rate of <1 (and thus reduce the case numbers year on year). Specifically, this threshold is obtained by estimating (λ – r₁) from fitting the data, obtaining the estimate of λ, denoted by subtraction based on the r₁ value obtained from the assumed testing frequency and test sensitivity. The potential net reproduction corresponding to future alternative testing frequency d′ and/or test sensitivity p′ is

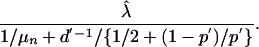For example, if the true test sensitivity over the period analyzed was 66.7% and testing had been annual in the Western Region, then an increase in test sensitivity to ≈73% would be sufficient to drop the reproduction rate to <1. Alternatively, if the true test sensitivity over the period analyzed was 80% and testing was annual in the Western Region, then an increase in test sensitivity to ≈85% would be sufficient. Finally, if the true test sensitivity over the period analyzed was 90% and testing was annual in the Western Region, then an increase in test sensitivity to ≈94% would be sufficient. Alternatively, in each of these cases, an increase in testing from annual to every 10 months was sufficient to drop the reproduction rate to <1.

These illustrative results demonstrate that although the net reproduction number is clearly >1, it is sufficiently close to 1 that relatively modest improvements either in test performance or testing frequency would be sufficient to bring the epidemic under control, under the highly idealized assumptions made in this model.

Discussion and Further Developments

The estimates for net reproduction number for TB in cattle ranged from 1.02 to 1.11. Published estimates for the basic reproduction number for M. bovis infections wildlife species have varied considerably between and within species partly as a function of density: 1.2 in badgers in Great Britain (14), 1.6–2.1 in brushtail possums in New Zealand (15, 16), and 0.2–1.2 in ferrets in New Zealand (17). For comparison, the basic reproduction number for human TB in England and Wales dropped from ≈3 in 1900 to 2 by 1950 and fell to <1in ≈1960, with the net reproduction number remaining at ≈1 from 1900 to 1950 (18).

There are many possible extensions of the above analysis. For example, spatial aspects can be represented by having a larger discrete set of intercommunicating systems, each of the above type supplemented by some possibility of transmission of disease from one site to another. There are no mathematical difficulties in analyzing such a model; we have not done so because of the absence of the data needed to specify the numerical values of the necessary parameters. Detail on variation in testing frequency in different regions also could be analyzed simultaneously in a similar set of expanded transmission equations.

By using analytical solutions to relatively simple transmission models, this analysis provides clear estimates of the net reproduction number of bovine TB in Great Britain. This number can be used to predict the impact of additional control measures such as increased testing frequency (whether on a parish or regional basis or through the imposition of additional restrictions on cattle herds with overdue skin tests) and/or increased test sensitivity (whether through the improved application of the tuberculin skin test, wider use of the so-called “severe interpretation” of the skin test, or parallel use of other diagnostic tools such as the γ-IFN test).

Although useful insight can certainly be gained from more complex, geographically specific models such as that used to analyze data on cattle movements (19) or to simulate the impact of badger-control strategies on TB incidence in cattle (20–22), the key benefit of models such as those presented here is the logical transparency and relative simplicity of the results. This approach is in keeping with the preference for simpler model formulations, in the face of parameter and other uncertainties, expressed by the Royal Society Report Infectious Diseases of Livestock (23). Clearly, as more data become available, the model can be extended.