Probing the transition state via photoelectron and photodetachment spectroscopy of H₃O⁻

Abstract

The H₃O⁻ anion has stable and metastable structures that resemble configurations in the vicinity of the transition state for the neutral reactions OH + H₂ ↔ H₂O + H. Photoelectron spectroscopy of this anion probes the neutral reaction dynamics in the critical transition-state region. Accurate quantum dynamics calculations of the photoelectron intensity and photodissociation product energies are shown to provide a quantitatively reliable means of interpreting such experimental observations and reveal a detailed picture of the reaction dynamics.

Since the first detailed studies of elementary chemical reactions at the molecular level, both experimentalists and theoreticians have attempted to probe and understand the dynamics of the critical transition state that separates reactants and products. Several years ago, Neumark and coworkers (1–3) established the use of photoelectron spectroscopy to directly probe the molecular dynamics in the vicinity of a transition state. For several molecules, the stable anion has an equilibrium geometry that resembles the geometry of the transition state for a reaction involving the corresponding neutral molecule—e.g., FH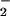 and the transition state for the reaction F + H₂ → FH + H. Photoemission of an electron therefore creates, according to the Franck–Condon principle, the neutral molecule in the vicinity of the transition state. Photoelectron spectroscopy measures the kinetic energy distribution of the ejected electron and thereby probes the molecular states in the transition state region. The combination of such experiments with accurate ab initio calculation of the potential energy surfaces (PESs) of the neutral specie and anion, and with exact quantum scattering calculations of the motion of the atomic nuclei, resulted in a quantitative understanding of the transition-state dynamics for the F + H₂ reaction (4).

Since this work, a number of relevant advances have been made in both theory and experiment. In an important paper, the Berkeley group combined with Gunion and Lineberger (5) to report independent measurements of the photoelectron spectroscopy of the polyatomic anions H₃O⁻ and D₃O⁻. These experiments probed the transition state for the reactions:

1

These tetra-atomic reactions have become the prototypes for the study of polyatomic reactions in which different vibrational modes can play a role in the reaction dynamics (6–13). Recently, Continetti and coworkers (14–18) have developed photoelectron-photodetachment coincidence spectroscopy to simultaneously measure the energy distribution of the ejected electron and the kinetic energy of the fragments resulting from dissociation of the unstable neutral molecule. This technique has been applied to the transition-state spectroscopy of a number of polyatomic anions, although not yet to H₃O⁻. Also recently, this type of coincidence spectroscopy has been applied with femtosecond time resolution to neutral species (19). Approximate reduced-dimensional model theoretical studies of the photoelectron spectroscopy of H₃O⁻ have been reported (20–24). However, again recently, theoretical methods have been developed to construct accurate ab initio molecular PES for tetra-atomic systems in the full six dimensions (25–27). Moreover, new theoretical methods now allow evaluation of the exact quantum dynamics of tetra-atomic reactions (28–30). Hence, all of the necessary methods are now available to combine quantitatively accurate theory and experiment in a study of transition-state spectroscopy for H₃O⁻ and other tetra-atomic molecules.

We report quantitatively accurate calculations of the photoelectron-photodetachment coincidence spectra of H₃O⁻ from first principles. The calculated photoelectron spectra, with no empirical adjustment, are in excellent agreement with the experimental data. A detailed assignment of the spectral features is presented, and an examination of the rotational states of the photofragments provides additional insight into the dynamics. The calculated photoelectron-photodetachment coincidence spectrum is presented as a prediction.

These calculations are based on highly accurate ab initio calculations of the molecular potential energy surfaces for both H₃O and H₃O⁻. The PES for H₃O has been reported (31, 32). The PES for H₃O⁻ has been constructed by using the same interpolation methods used for the neutral system. Initially, the PES was constructed with ab initio calculations of the electronic energies, energy derivatives, and second derivatives at a relatively high level of theory—the spin restricted, coupled cluster method, including single and double excitations with perturbative account of triple excitations, using an augmented, correlation consistent, polarized valence triple zeta quality basis set [CCSD(T)/aug-cc-pVTZ]. The energy of each geometry in the interpolation data set was replaced with the corresponding value for a larger basis set, CCSD(T)/aug-cc-pVQZ. This later level of theory was also used for energies in the data set for the neutral molecule. Hence, the relative energies of molecular configurations for both anion and neutral specie can be calculated directly, without any empirical adjustment. Details of the PES for H₃O⁻ will be reported elsewhere. Fig. 1 provides a schematic representation of the energy profiles of paths linking important stationary points on the PES for H₃O and H₃O⁻.

Figure 1.

(A) A contour plot of the minimum potential energy for OH + H₂ is shown in the vicinity of the saddle point as a function of the forming O … H and breaking H … H bond lengths. Contour plots of the probability distribution for these two bond lengths are also shown for the ground state of H₃O⁻ (red) and the excited initial state (blue). (B) A schematic representation of the relative energies of some features on the PESs for H₃O and H₃O⁻.

In the photoelectron emission, an initial rovibrational state of H₃O⁻, Φ_i, evolves into a scattering wavefunction, on the dissociative PES of the neutral H₃O. The scattering wave with energy E may be decomposed into components, ψ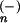(E), corresponding to eigenstates of the asymptotic dissociated fragments, which we label with a generic quantum number, n, and associated channel basis function, φ_n. The photoelectron spectrum associated with the photoproduct state n can be simulated by calculating the simple Franck–Condon factor (3, 33, 34):

2

The total photoelectron spectrum is simply a sum of these contributions from all energetically possible final product states. In this work, P_n←i(E) is calculated via a time-dependent wave packet method (35) in which we evaluate the time-independent components of the initial state in the asymptotic region with the reaction coordinate R = R_L and expand these components in terms of φ_n,

3

Here the time evolution is determined by the Hamiltonian, Ĥ, for the neutral molecule. It can be shown (35) that each component of the photoelectron spectrum is obtained from the asymptotic expansion by

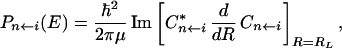4

where μ is the corresponding reduced mass for the reaction coordinate R.

Two different initial rovibrational states of H₃O⁻ have been considered. To begin, the bound vibrational states with zero angular momentum (J = 0) were evaluated. The ground state has a zero point energy of 5,990 cm⁻¹ (0.7425 eV). The accuracy of this value is indicated by the calculated dissociation energies from this ground state: For H₂O + H⁻ (OH⁻ + H₂) the calculated dissociation energy at 0 K is 0.666 eV (0.232 eV), which is consistent with the observed value of 0.62 ± 0.04 eV (0.20 ± 0.04 eV) at 298 K (36). The first few vibrational excitation energies are near 408, 423, 519, 541, and 582 cm⁻¹. Actually, each of these energies encompasses a multiplet of states split by tunneling between equivalent minima on the PES (there are six possible permutations of the indistinguishable hydrogens). However, the splitting is very small (below 1 cm⁻¹ for the ground state) and is not considered here. The ground and first excited states are localized in the region of the [HOH… H]⁻ well of Fig. 1B. The energy of the first excited vibrational state is sufficiently high to ensure a low population in this state at room temperature. Hence, we have evaluated the photoelectron and photodissociation spectra for an initial state given by the ground state only. In the original experiments, an attempt was made to prepare H₃O⁻ in the OH⁻… H₂ structure (5). To simulate this situation, we have first determined that the second (423 cm⁻¹) and fifth (582 cm⁻¹) vibrationally excited states are strongly localized in the region of the [HO… H₂]⁻ well of Fig. 1B. At room temperature, these are the only such localized states to have significant population. Since there is no significant tunneling to energy minima in which the free OH bond of Fig. 1B is bonded, the free hydrogen can be treated as a spectator, and only the permutation symmetry of the bonded hydrogens need be considered. The initial state corresponding to the [HO… H₂]⁻ structure is therefore taken to consist of 75% of a state with ortho-H₂ symmetry and 25% of a state with para-H₂ symmetry. At 300 K, each of the ortho and para states has about 80% (20%) probability of being in the second (fifth) excited state. This initial state is simply referred to hereafter as the excited initial state. The calculation of the photoelectron spectrum is actually performed for each eigenstate in the initial wavepacket, and the total spectrum is obtained as the appropriately weighted sum, expressed as a function of the electron binding energy, eBE:

5

where eKE is the observed kinetic energy of the photoelectron, hν is the photon energy, and E_init is the energy of the initial eigenstate of H₃O⁻. It is also convenient to partition eBE as:

6

where E(H₂O +H) is the ground-state energy of the H + H₂O product, so that E_fragment is the total energy available to the products and E_binding is the binding energy of H₃O⁻ relative to the ground state of the products. For the ab initio PESs, E_binding is about 1.29 eV for the ground state.

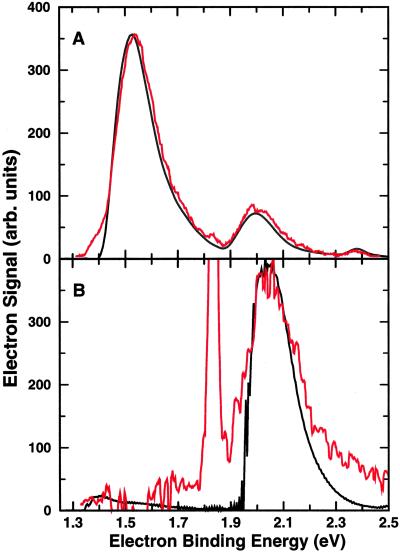
Fig. 1A gives a schematic representation of the initial conditions for the nuclear dynamics. The square modulus of the ground (excited) state nuclear wavefunction for H₃O⁻, shown in red (blue), is projected above a contour plot of the PES for the neutral H₃O. Fig. 2 compares the calculated and experimental photoelectron spectra. Fig. 2A compares the calculated spectrum for the ground state of H₃O⁻ with the experimental spectrum that was obtained with a zero angle between the laser polarization and direction of electron detection, Θ = 0 (from figure 2b of ref. 5). In Fig. 2B, the experimental data for Θ = 90 (from figure 11a of ref. 5) are compared with the calculated spectrum for the excited initial state of H₃O⁻. The sharp intense experimental feature in Fig. 2B is due to OH⁻ and is ignored here. The spectrum in Fig. 2A had been assigned to photoemission from the ground state that resembles [HOH … H]⁻ (5). This assignment is completely consistent with the present calculation; indeed, the agreement for this assignment is clearly excellent. On the basis of the polarization (Θ) dependence and the expected anisotropy, it was argued (5) that the peak near eBE = 2.05 eV in the spectrum for Θ = 90 might be due to photoemission from anion structures resembling [HO … H₂]⁻. Again, this assignment is strongly supported by the current calculations, since the excited initial state was chosen to correspond to metastable [HO … H₂]⁻ at room temperature. It is important to note that there has been no adjustment of the energy scale for the theoretical results, so that the coincidence of the peaks in these spectra is a measure of the agreement between theory and experiment. Moreover, although the total intensity scales for theory and experiment are arbitrary, the relative peak heights and shapes are also a direct measure of the agreement between theory and experiment. Note also that the position of the calculated peak in Fig. 2B is not very sensitive to the proportion of the excited initial state allocated to the fifth vibrationally excited state of the anion (here about 20%), as both the second and fifth excited states lead to maximum intensity at similar values of eBE. The major peak in Fig. 2B corresponds to formation of the HO + H₂ product, whereas the small peak at about 1.4 eV corresponds to formation of H₂O + H. Overall, the photoproduct branching ratio for [H₂O + H]:[HO + H₂] is 1:16.

Figure 2.

(A) The probability of observing photoelectrons as a function of the electron binding energy, calculated for the ground state of H₃O⁻, is compared with the observed intensity (red) of photoelectrons at Θ = 0. (B) The probability of observing photoelectrons as a function of the electron binding energy, calculated for the excited initial state of H₃O⁻, is compared with the observed intensity (red) of photoelectrons at Θ = 90.

Fig. 3 shows the deconvolution of the calculated intensity of Fig. 2A into contributions from various final states of the neutral. Overall, the photoproduct branching ratio for [H₂O + H]:[HO + H₂] is 195:1. Each individual intensity distribution is proportional to the probability of creating each state in the photoproducts. Fig. 3A presents the contribution of different vibrational states of the products, while these states are further resolved into rotational state contributions in Fig. 3B. The local mode stretching states are mixtures of the symmetric and antisymmetric normal mode states. As might be expected from Fig. 1B, photoelectron emission from the ground-state anion results in photodissociation to H + H₂O, predominately. The current calculations confirm earlier suggestions (5, 20–22) that the major peak in Fig. 3A corresponds to formation of H₂O in its ground vibrational state. The smaller peak in Fig. 3A, near eBE = 2 eV, is almost entirely associated with production of the H₂O with one quantum in the stretching mode (5, 20–22), whereas the very small feature near eBE = 2.4 eV corresponds to two quanta in this mode with a minor component corresponding to production of OH and H₂. Fig. 3B indicates that the asymmetry of the experimental peak shapes is due to rotational transitions, and that the most populated rotational state in the vibrational ground state is j = 3.

Figure 3.

(A) The calculated photoelectron intensity associated with vibrational states of the products is shown as a function of the electron binding energy. Vibrational states are written as (mn)(k) to denote m quanta in one local OH stretching mode, n quanta in the other, and k quanta in the bending mode. The small contribution from H₂ + OH is not state resolved. (B) The contribution to the photoelectron intensity associated with each rotational angular momenta (J = 0–10) of H₂O is shown as a function of the electron binding energy. (Left) Contributions for zero quanta of OH stretching excitation. (Right) Contributions for one quanta of OH stretching excitation.

The question arises as to whether ionization to excited states of the neutral molecule can play a role in these experiments. The ground state of the neutral in planar geometries is a 2A′ state, whereas the first excited state has 2A" symmetry. The 2A" channel is energetically closed in the H₂O + H asymptote, and our preliminary calculations suggest that vertical ionization to this state at the [HOH … H]⁻ minimum energy structure is also impossible at the photon energies used in the experiments. Hence, the 2A" state is unlikely to be significant in the experiment of Fig. 2A. In contrast, the 2A′ and 2A" states are degenerate in the OH + H₂ asymptote. Moreover, our preliminary calculations and an earlier report (37) suggest that the energy gap between the two states is only of the order of 0.01–0.1 eV near the [HO … H₂]⁻ local minimum energy structure. Hence, although excitation to the 2A" state may play a role in the experiment of Fig. 2B, it may be difficult to distinguish this process from excitation to the 2A′ state. An investigation of the subtle effect of dynamics on this excited state, and possible nonadiabatic dynamics involving coupling to the 2A′ state, is not feasible at present.

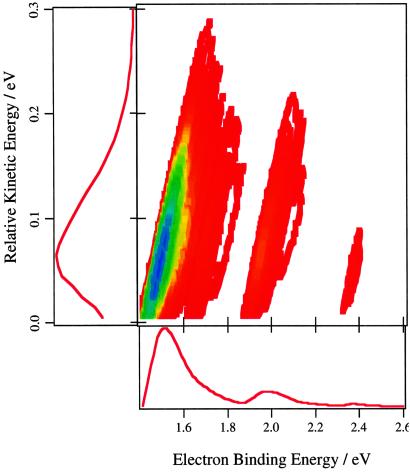
Fig. 4 presents a prediction for the photoelectron-photodetachment spectrum of ground state H₃O⁻. The spectrum is dominated by production of H₂O in a distribution of rotational levels of the ground vibrational state. For a given photoelectron kinetic energy, this spectrum directly measures the partitioning of the energy available to the photofragments into internal (rovibrational) excitation versus relative kinetic energy. Since the binding energy, E_binding, is about 1.29 eV, calculations using the distribution in Fig. 4 show that the average energy available to the H + H₂O product is about 0.37 eV, and that about 25% of this energy is in relative translation of the products.

Figure 4.

The photoelectron-photodissociation coincidence spectrum is presented as a contour plot of the distribution of photoelectron intensity (red = low, blue = high) as a function of the electron binding energy and relative translational energy of the photofragments. The corresponding partially averaged distributions are also shown.

The very close agreement between the photoelectron spectra and the first principles theoretical calculations shows that theory is capable of a providing quantitatively reliable means of interpreting such experimental observations. Measurement of the photoelectron-photodetachment coincidence spectrum for H₃O⁻ at high resolution could now be combined with these very accurate calculations to expose the detailed dynamics of the reaction in the vicinity of the critical transition state.

Abbreviation

PES

potential energy surface