Loss of microsatellite diversity and low effective population size in an overexploited population of New Zealand snapper (Pagrus auratus)

Abstract

Although the effects of overfishing on species diversity and abundance are well documented, threats to the genetic diversity of marine fish populations have so far been largely neglected. Indeed, there seems to be little cause for concern, as even “collapsed” stocks usually consist of several million individuals, whereas population genetics theory suggests that only very small populations suffer significant loss of genetic diversity. On the other hand, in many marine species the genetically effective population size (N_e), which determines the genetic properties of a population, may be orders of magnitude smaller than the census population size (N). Here, microsatellite analyses of a time series of archived scales demonstrated a significant decline in genetic diversity in a New Zealand snapper population during its exploitation history. Effective population sizes estimated both from the decline in heterozygosity and from temporal fluctuations in allele frequency were five orders of magnitude smaller than census population sizes from fishery data. If such low N_e/N ratios are commonplace in marine species, many exploited marine fish stocks may be in danger of losing genetic variability, potentially resulting in reduced adaptability, population persistence, and productivity.

In 1883, Thomas Huxley, then president of the Royal Society of London, declared that “the cod fishery, the herring fishery and probably all of the great sea fisheries are inexhaustible; that is to say that nothing we do seriously affects the numbers of fish” (1). Since then, the status of the major fisheries and its perception by fisheries scientists has changed considerably. Several cod and herring fisheries have had high profile “collapses” in recent decades (2), and in 1997, it was estimated that 60% of the major marine fisheries were either fully exploited or overexploited (3). Such high levels of exploitation not only affect the abundance of target species (4) but also change the physical (5) and trophic (6) structure of marine ecosystems. Among attempts to ameliorate such immediate far-reaching ecological effects of fishing, there is usually little consideration for more long-term impacts, such as changes in the genetic constitution of exploited species. Although there has been some interest in selective changes in exploited fish populations (7), their genetic diversity is generally considered to be unaffected by commercial fishing, in an attitude that echoes Huxley's statement of more than a century ago. Indeed, population genetics theory suggests that genetic diversity is significantly reduced only in very small populations (8), and so even “collapsed” stocks may consist of far too many fish to show declines in genetic diversity measurable with feasible sample sizes (9). For example, the spawning stock biomass of the Newfoundland cod, whose fishery was so famously closed in 1992, remained at 22,000 t [ref. 10; 1 t (tonne) = 1,000 kg], leaving several million fish in the population. Similarly, even after stock crashes and effective cessation of dependent fisheries, the stock biomass of many small pelagic species is generally still several tens of thousands of tonnes, and thus populations typically consist of tens of millions of fish (11). These population sizes are many orders of magnitude higher than those commonly considered being in danger of losing genetic diversity (8), and so there appears to be little cause for concern from a genetic perspective.

On the other hand, the number of fish in a population (census population size, N) is often much larger than the genetically effective population size (N_e), which determines the genetic properties of a population (12). The long-term evolutionary N_e is often orders of magnitude smaller than current population sizes, probably because of historic population bottlenecks, “selective sweeps,” or colonization histories (13). However, recent evidence suggests that even the short-term N_e without consideration of such historical events may be very much lower than census population numbers. Especially in marine organisms, high fecundity, a strong bias in reproductive success, large variations in year class strength, and size-dependent fecundity may reduce the effective population size by several orders of magnitude (14). Millions of individuals may therefore be equivalent to an effective population size of only hundreds or thousands. The notion that collapsed fish stocks may lose genetic diversity is thus not as far-fetched as is often assumed, despite their large spawning stock biomasses.

The demonstration of changes in genetic diversity in wild populations is often complicated by the lack of suitable populations for comparison. Most commercially exploited species are fished wherever they occur, and thus comparisons between exploited and unexploited stocks are not possible. Temporal comparisons based on archived material such as scales, otoliths, and bones, on the other hand (15), are usually restricted by a lack of preexploitation samples, as routine sampling is usually initiated long after the onset of the commercial fishery. Here, we used a collection of scales of two New Zealand snapper (Pagrus auratus) populations, dating back in one population to the beginning of exploitation, to investigate the genetic effects of reductions in stock biomass caused by commercial fishing.

The history of the snapper fishery in the north of New Zealand is typical for many other fisheries in the world (16, 17): yields of the commercial fishery in Hauraki Gulf (Fig. 1), which developed in the mid 1800s, increased slowly up to the 1970s, when the introduction of pair trawls raised catches to 12,000 t (Fig. 2). By the mid-1980s annual catches had declined to 6,000 t, and stocks showed signs of overfishing. During this period, the spawning stock biomass had decreased from an estimated 280,000 t to 37,000 t, a decline by 87%, although population abundance never fell below 37 million individuals (17). Because of the importance of the fishery and the drastic decrease in stock abundance, research on snapper biology started soon after World War II, not only in the heavily fished northern populations, but also in hitherto less exploited stocks in the south, such as Tasman Bay in the north of the South Island. There are therefore time series of scale samples from Tasman Bay, beginning in 1950 just after the commencement of the fishery, when spawning stock biomass was essentially at natural levels, and covering the entire exploitation history of the stock, with a reduction in biomass by 85% and in numbers by 75%, and an estimated minimum population size of 3.3 million fish in 1985 (refs. 16 and 18; Fig. 2; ref. 18 is available at www.fish.govt.nz/sustainability/research/assessment/plenary/SNA_2&7_FAR_Apr2002.pdf). There is no, or very little, exchange between the two snapper populations, which thus experienced independent exploitation and demographic histories. Allozyme variation (19), growth rates (20), and microsatellite polymorphism (21) show that the Hauraki Gulf population is part of a larger stock along the northeast coast of the North Island, whereas the Tasman Bay fish are differentiated from the Hauraki Gulf stock and appear to be isolated from other populations. A comparison between the two populations in Hauraki Gulf and Tasman Bay therefore allowed an assessment of the genetic effects of different exploitation histories and population sizes.

Figure 1.

Map of New Zealand showing the sampling sites .

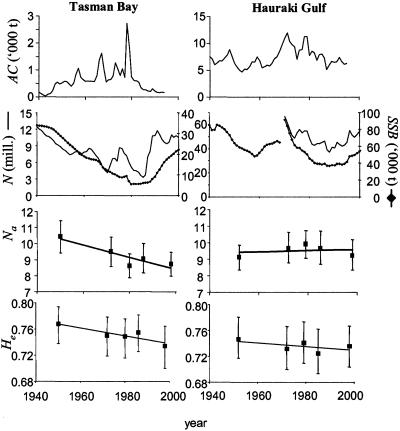
Figure 2.

Temporal changes in annual catch (AC; ref. 16), spawning stock numbers (N; refs. 17 and 18) and biomass (SSB), genetic diversity (mean number of alleles per locus (N_a), and mean expected heterozygosity (H_e); both means ± 95% confidence limits of 30 individuals) in New Zealand snapper (Pagrus auratus). In Hauraki Gulf, estimates of SSB before 1970 are from ref. 16; after 1970, from ref. 17.

Materials and Methods

Molecular Work.

Dried scales from 1950 to 1986 were obtained from the Ministry of Fisheries, Wellington, New Zealand, where they had been stored individually at room temperature in paper envelopes. DNA from scales was extracted in a dedicated ancient DNA laboratory by using a previously published protocol (22). Additional samples were obtained from fresh material collected in 1998, and DNA was extracted by using standard methods. DNA extracts were screened at seven microsatellite loci [Pma1, Pma2, Pma5 (23); GA2A, GA2B, GT2, GT4 (22)] on an ALFexpress automated sequencer (Amersham Pharmacia Biotech). Sample sizes are presented in Table 1.

Table 1.

Measures of genetic variability at microsatellite loci

Locus		Tasman Bay					Hauraki Gulf
		1950	1972	1980	1986	1998	1952	1972	1979	1985	1998
GT2	n	54	46	31	50	47	39	49	38	49	49
	Ho	0.815	0.652	0.677	0.820	0.596	0.692	0.653	0.658	0.633	0.755
	He	0.777**	0.702	0.703	0.755	0.711	0.662	0.746	0.774	0.647	0.720
	Na	10	9	6	8	8	9	12	10	8	8
	Na (30)	9.2	7.5	6.0	6.9	7.8	8.0	9.5	9.4	6.9	7.4
GT4	n	55	48	31	49	40	39	48	44	46	49
	Ho	0.855	0.938	0.935	0.878	0.950	0.846	0.771	0.795	0.870	0.837
	He	0.890	0.863	0.896	0.875**	0.878	0.896	0.870	0.854	0.871	0.874
	Na	17	16	11	16	14	12	13	14	16	16
	Na (30)	13.9	12.8	10.9	13.6	13.1	11.4	11.6	11.5	13.9	13.0
GA2A	n	56	49	31	50	39	40	50	44	49	49
	Ho	0.821	0.837	0.903	0.900	0.821	0.925	0.800	0.864	0.796	0.755
	He	0.838	0.849	0.845	0.833	0.788	0.801	0.821	0.865	0.852	0.815
	Na	10	10	8	9	8	8	9	9	10	11
	Na (30)	9.3	8.2	8.0	8.1	7.5	7.5	8.4	8.7	8.8	9.3
GA2B	n	54	47	31	46	46	40	50	36	49	49
	Ho	0.778	0.851	0.839	0.913	0.739	0.900	0.720	0.778	0.837	0.653
	He	0.802	0.820	0.781	0.800	0.709	0.798	0.769	0.811	0.800	0.775
	Na	18	14	13	11	10	13	15	12	15	12
	Na (30)	14.1	12.4	12.8	10.3	8.5	11.8	12.1	11.6	12.6	10.7
Pma1	n	53	50	31	50	47	40	49	42	50	49
	Ho	0.679	0.760	0.645	0.720	0.574	0.725	0.612	0.810	0.720	0.633
	He	0.618	0.674	0.648	0.671	0.657	0.665	0.659	0.669	0.649	0.651
	Na	7	6	5	6	7	6	7	7	7	7
	Na (30)	5.9	5.6	5.0	5.8	6.2	5.7	6.7	6.6	6.4	6.2
Pma2	n	53	40	31	46	39	40	40	33	49	49
	Ho	0.811	0.800	0.871	0.848	0.821	0.725	0.675	0.697	0.714	0.776
	He	0.879*	0.815	0.851	0.870	0.876**	0.769	0.784*	0.740	0.825	0.755
	Na	18	13	11	15	14	14	15	15	15	15
	Na (30)	15.1	11.8	11.0	13.5	12.9	12.6	13.3	14.3	13.5	12.4
Pma5	n	56	50	31	50	42	40	48	45	50	48
	Ho	0.661	0.600	0.806	0.540	0.667	0.800	0.521	0.711	0.620	0.729
	He	0.605	0.600	0.611	0.527	0.550	0.663	0.569*	0.612	0.561	0.645
	Na	5	9	6	5	4	4	4	6	4	5
	Na (30)	4.4	6.8	5.9	4.2	3.7	4.0	3.6	5.0	3.6	4.5
Average (−GA2A)	n	54.2	46.8	31.0	48.5	43.5	39.7	47.3	39.7	48.8	48.8
	Ho	0.766	0.767	0.796	0.786	0.724	0.781	0.659	0.741	0.732	0.730
	He	0.762	0.746	0.748	0.750	0.730	0.742	0.733	0.743	0.726	0.737
	Na	12.5	11.2	8.7	10.2	9.5	9.7	11.0	10.7	10.8	10.5
	Na (30)	10.4	9.5	8.6	9.0	8.7	8.9	9.5	9.7	9.5	9.0

Sample size (n), observed heterozygosity (H_o), expected heterozygosity (H_e), number of alleles (N_a), and average number of alleles from 30 resampled individuals [N_a (30)] are tabulated. Deviation from Hardy–Weinberg equilibrium: 

^**, P < 0.01; 

^*, P < 0.05. 

Statistical Analyses.

Multilocus genotypes were tested for deviations from Hardy–Weinberg equilibrium and for linkage disequilibrium by using Fisher's exact test in genepop version 3.2 (24). Genetic diversity was quantified by using Nei's (25) unbiased heterozygosity (H_e) and the mean number of alleles per locus (N_a). Because the number of alleles strongly depends on the sample size, 30 individuals from each sample were resampled 1,000 times [by using PopTools (add-in for Microsoft Excel, written by Greg Wood, Commonwealth Scientific and Industrial Research Organization, Australia, available at www.cse.csiro.au/CDG/poptools/)], so not only standardizing the mean (sampling without replacement), but also providing estimates of the sampling variance (95% confidence limits, obtained with replacement). The statistical significance of temporal trends was tested by calculating slope (b) and Pearson's correlation coefficient (r) of a linear regression of Ĥ_e and N̂_a against year, permuting individuals among samples 1,000 times, and comparing the real parameters with randomized estimates. A linear regression was used as the most parsimonious model because the data suggested a linear relationship (Fig. 2) and there was no a priori information about changes in N_e as a basis of a more specific nonlinear model.

N̂_e was estimated from both temporal fluctuations in allele frequencies (26) and the decrease in heterozygosity (8, 25). The small sample of 1980 from Tasman Bay was excluded from the temporal analysis, because the method is sensitive to small sample sizes, and the sample was the only one collected from pair trawls. Calculation of N̂_e followed sampling plan 2 as the more parsimonious model, because the difference between sampling plans becomes negligible if N is large (26). Only data of time intervals of 20 years or more were used, because effective population size estimates may be biased in species with overlapping generations if the time interval between sampling events is short (27). Generation time (Ĝ) was estimated following Felsenstein (28) from age frequency data of three consecutive years (1998–2000) in both Tasman Bay and Hauraki Gulf. Fecundity was estimated from average fish weight in each age class (29).

The second method to estimate N̂_e used the decrease in heterozygosity (8, 25). To reduce random noise in the decrease of heterozygosity in a small population (30), a linear regression between heterozygosity and year was used to estimate effective population size over the entire period.

Yearly census sizes of the adult population were obtained from reports of the National Institute of Water and Atmospheric Research in New Zealand (17, 18). For N̂_e/N̂ ratios, the harmonic mean of the annual N̂ in specific time periods was used (31).

Results

Deviations from Hardy–Weinberg equilibrium were detected in 6 of 70 tests (Table 1); four of these deviations were due to heterozygote deficiencies, and no test was significant after Bonferroni correction. Loci GA2A and GA2B were isolated from the same clone and were significantly linked in 8 of the 10 samples (TB50, TB80, TB86, TB98, HG52, HG72, HG79, HG98)—therefore, locus GA2A (the locus with fewer alleles and thus with theoretically lower power in detecting reduction in genetic diversity) was excluded a priori from averages.

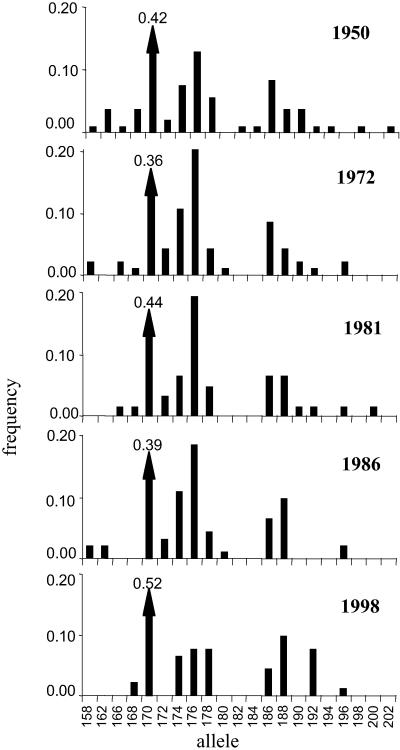
Estimates of genetic diversity and their 95% confidence limits (Fig. 2) showed a decline of both mean heterozygosity (N̂_e) and mean number of alleles (N̂_a) in Tasman Bay, whereas there were only random fluctuations of genetic diversity in Hauraki Gulf. Permutation tests showed that this decline of genetic diversity over all loci was significant in Tasman Bay, but not in Hauraki Gulf (Table 2). Furthermore, linear regressions of individual locus diversity against year show a decrease in genetic diversity of the Tasman Bay population over time in six of the seven loci. In contrast, only one locus decreased in both heterozygosity and the number of alleles in Hauraki Gulf. The effective population size estimated from the linear regression of mean heterozygosity against year in Tasman Bay was 46 individuals. Individual loci showed clear effects of genetic drift, such as fluctuations in allele frequencies and loss of rare alleles (Fig. 3).

Table 2.

Slopes and Pearson's correlation coefficients of regressions of genetic diversity (number of alleles N_a and heterozygosity H_e) at individual loci, and of the average across loci (excluding GA2A, see text)

Locus		Tasman Bay		Hauraki Gulf
		Pearson	Slope	Pearson	Slope
GT2	He	−0.57	−0.001	0.25	0.001
	Na	−0.60	−0.040	−0.34	−0.023
GT4	He	−0.37	0.000	−0.53	0.000
	Na	−0.29	−0.019	0.68	0.044
GA2A	He	−0.67	−0.001	0.39	0.001
	Na	−0.97	−0.035	1.00	0.040
GA2B	He	−0.70	−0.002	−0.21	0.000
	Na	−0.91	−0.112	−0.43	−0.018
Pma1	He	0.63	0.001	−0.64	0.000
	Na	0.15	0.004	0.41	0.009
Pma2	He	0.03	0.000	0.02	0.000
	Na	−0.46	−0.040	0.02	0.001
Pma5	He	−0.69	−0.001	−0.23	−0.001
	Na	−0.25	−0.018	0.27	0.010
Mean (−GA2A)	He	−0.90*	−0.001ns	−0.33ns	0.000ns
	Na	−0.91*	−0.038**	0.20ns	0.004ns

Results of tests for significance are shown for the average across loci: 

^**, P < 0.01; 

^*, P < 0.05; ns, P > 0.05. 

Figure 3.

Allele frequencies of locus GA2B in Tasman Bay, showing random genetic drift and loss of alleles. The frequency of the most common allele (170) is indicated above the arrow.

Temporal changes in allele frequencies in both populations were used to estimate effective population sizes (Table 3). Mean generation time (Ĝ) was estimated at 11.4 years in Hauraki Gulf and 13 years in Tasman Bay, although varying G between 10 and 15 years had only limited effects on the N̂_e estimate (83–125% of the point estimate at 13 years in Tasman Bay). In Tasman Bay, the estimated effective population size over the whole time period (1950–1998), spanning almost four generations, was about 180 individuals, and was significantly different from infinity (95% confidence limits: 80–720 individuals). With the exception of the first time period, the N̂_e/N̂ ratio estimated from our genetic data and from fisheries data remained remarkably constant at 1.8–2.8 × 10⁻⁵. In Hauraki Gulf, on the other hand, the estimate over the whole study period (1952–1998) was not significantly different from infinity, as were all individual estimates with one exception (1972–1998).

Table 3.

Number of generations (Ĝ), F values, and estimates of effective (N̂_e) and harmonic means of census population size (N̂) in Tasman Bay and Hauraki Gulf

	Tasman Bay				Hauraki Gulf
	1950–1972	1950–1986	1972–1998	1950–1998	1952–1972	1952–1979	1952–1985	1972–1998	1952–1998
Ĝ	1.7	2.8	2.0	3.7	1.8	2.4	2.9	2.3	4.0
F̂GT2	0.018	0.014	0.030	0.030	0.025	0.047	0.018	0.022	0.024
F̂GT4	0.019	0.033	0.025	0.032	0.035	0.036	0.031	0.039	0.029
F̂GA2A	0.034	0.025	0.058	0.028	0.022	0.059	0.025	0.012	0.019
F̂GA2B	0.019	0.024	0.046	0.032	0.017	0.031	0.025	0.023	0.012
F̂Pma1	0.026	0.044	0.008	0.031	0.060	0.036	0.012	0.044	0.012
F̂Pma2	0.025	0.030	0.040	0.034	0.034	0.024	0.024	0.028	0.033
F̂Pma5	0.021	0.024	0.018	0.021	0.056	0.041	0.053	0.034	0.030
F̂all (−GA2A)	0.021	0.028	0.031	0.032	0.032	0.034	0.026	0.030	0.025
N̂e	1,152	171	117	176	104	138	476	126	1,164
95% C.l.	95–∞	72–1,238	46–2,205	80–720	39–∞	50–∞	98–∞	53–834	157–∞
N̂ (×106)	6.9	6.2	6.7	6.8	72	66	61	46	55
N̂e/N̂ (×10−5)	16.7	2.8	1.8	2.6	0.17	0.25	0.94	0.27	0.25

For the Hauraki Gulf population, census population sizes were available only from 1970 onwards. C.l., confidence limits. 

Discussion

Our data provide evidence for a loss of genetic diversity in an exploited fish population, despite an estimated minimum census population size of more than 3 million fish. Such a decrease in diversity implies that the effective population size was several orders of magnitude smaller than census numbers. These results suggest that commercial fishing may result not only in selective genetic changes in exploited stocks (32) but also in reduced genetic diversity caused by genetic drift. Subsequently, we will place the evidence into a genetic and demographic context and investigate the wider implications of our study for commercially exploited marine fish species.

Loss of Genetic Diversity.

In Tasman Bay, there was a significant decrease in both heterozygosity and the mean number of alleles over the 50 years since the onset of exploitation. There are several possible explanations for such a finding: sampling bias, selection or selective sweeps, immigration, or genetic drift. Sampling bias is unlikely, as the decrease in diversity was observed over five independent sampling occasions and at six of seven loci. It is also unlikely that selective effects occurred at six of seven loci in Tasman Bay. Furthermore, although environmental conditions, in particular temperatures, are unstable and temporally unsuitable for snapper recruitment (16), growth rates of adult fish are higher than in the north of New Zealand (20), suggesting a benign environment at least for adult growth. It may be possible that the decrease in diversity was caused by immigration from a population with lower genetic diversity; however, a population survey failed to identify such a low-diversity population in New Zealand (21). Thus, genetic drift within the Tasman Bay population is the most likely explanation for the loss in diversity, implying a low effective population size and low N_e/N ratio.

Genetic diversity was higher in the Tasman Bay population than in Hauraki Gulf in 1950, but lower in 1998. Considering that genetic diversity is usually directly related to population size (33) and that the virgin stock biomass of the Hauraki Gulf population was almost 10 times larger than in Tasman Bay (280,000 vs. 35,000 t), the discrepancy of the 1950 estimates may suggest that genetic diversity had already been lost from the Hauraki Gulf population by 1950. Ryman et al. (7) suggested that large populations decreasing to moderate size might lose more rare alleles than medium-sized populations experiencing a severe bottleneck. The loss of genetic diversity may therefore be particularly pronounced during the initial stages of exploitation, and investigations in the advanced stages of exploitation history may be less likely to detect significant changes in allelic diversity (15).

Effective Population Size.

The effective population size was estimated by using two methods: (i) the decrease in heterozygosity (8, 25), and (ii) the temporal method (26). Both methods provided similar estimates of N̂_e in Tasman Bay between 1950 and 1998 [Ĥ_e: N̂_e = 46; temporal N̂_e = 176 (95% confidence limits: 80–720)]. Furthermore, with the exception of the first time period, the N̂_e/N̂ ratio in Tasman Bay remained remarkably constant over time, suggesting that N̂_e is determined by biological factors rather than sampling error or statistical artifacts. The higher N̂_e/N̂ ratio in the period 1950–1972 may be because of an overestimate of N̂_e from the temporal method, as the loss of heterozygosity suggested an N̂_e of only 35 individuals. However, the general concordance between the estimates of the two methods and the constant relationship to fishery data support the biological reality of N̂_e estimates.

The temporal method (26) assumes discrete generations, as well as samples drawn randomly from the entire generation. In species with overlapping generations and with samples biased toward specific age classes, temporal changes in allele frequencies are dependent not only on N_e but also on genetic differences between cohorts (27). This downward bias in the N̂_e estimate becomes smaller with increasing time between sampling occasions, as the contribution of genetic drift to temporal shifts in allele frequencies relative to differences between cohorts increases with the number of generations between sampling occasions (27). Such a positive correlation between length of time interval and N̂_e was not apparent in our data from Tasman Bay, as the N̂_e estimate over the whole time period was similar to the estimates in 1950–1986 and 1972–1998, and smaller than in 1950–1972. This suggests that our estimates of N̂_e are not overly biased and are likely to be in the correct order of magnitude, despite samples consisting mainly of 3- to 4-year-old fish (P.J.S., unpublished observation). The small effect of biased sampling may be caused by the contribution of many age classes to each cohort in the long-lived snapper, thus minimizing genetic differences among age classes (27).

The temporal method also assumes no immigration, an assumption that is difficult to prove in marine populations. However, there is strong evidence from allozyme (19) and microsatellite (21) data as well as from oceanographic patterns (34) that the Tasman Bay population is isolated from other snapper populations in New Zealand. Furthermore, if the low N̂_e estimates were caused by immigration, the source population would necessarily have to exhibit considerably lower diversity to produce the observed reduction in genetic diversity in Tasman Bay, and there was no evidence for such a population in a recent population survey (21). Thus immigration is an unlikely cause of the observed estimates of N̂_e and genetic diversity.

Estimates of N̂_e were very low in Hauraki Gulf, although not significantly different from infinity, with the exception of the period between 1972 and 1998. Although this was also the time of the lowest spawning stock biomass (Fig. 2), the N̂_e/N̂ ratio was an order of magnitude lower than that in Tasman Bay. As N̂_e was high (and nonsignificant) over the whole study period (N_e = 1,164) and there was no decrease in genetic diversity (Fig. 2), the low N̂_e value in 1972–1998 may have been an underestimate because of a statistical artifact, immigration from other populations, or other factors.

Collectively, our data strongly suggest an N̂_e/N̂ ratio of 10⁻⁵ in Tasman Bay, which is considerably lower than many previously published empirical (12) and theoretical estimates (35). However, these published estimates either do not include marine species (12) or fail to consider some of the ecological features of many marine fish. For example, snapper are extremely long lived (up to 50 years) and have indeterminate growth and strong weight-dependent fecundity (29), and thus a few old fish are likely to contribute disproportionally to overall recruitment. This variation in lifetime reproductive success estimated from age distributions alone leads to a standardized variance in fecundity of 1.9 and an N̂_e/N̂ of 0.46, whereas variances of more than 1 are usually considered exceptional (36). Furthermore, older and larger fish produce not only more but also larger eggs (37), which may improve survival and growth of their offspring (38), and thus further increase the bias in lifetime reproductive success among individuals. Possibly most importantly, survival of larvae may depend crucially on chance encounters with suitable plankton patches (see match-mismatch hypothesis in ref. 39), and much of the early mortality may be family specific and thus decrease N_e (40). In addition, Tasman Bay is at the southern edge of the species' distribution, and cold conditions during El Niño years often result in complete recruitment failure (16). Other factors, such as mating behavior and effective sex ratios, may further decrease the N_e/N ratio, although more information on the reproductive ecology of snapper would be required to evaluate the specific biological mechanisms.

Discrepancies between effective and census population sizes of two to five orders of magnitude appear to be common in marine species. For example, the female effective population size of red drum (Sciaenops ocellatus) in the Gulf of Mexico, estimated from temporal mitochondrial DNA data, is 4 × 10⁻³ that of the female census population size (41). More recent estimates based on microsatellites suggest an N̂_e/N̂ ratio of 10⁻⁴ (42). Similarly, the N̂_e/N̂ ratio of vermilion snapper (Rhomboplites aurorubens), an ecologically similar species, has been estimated to be an order of magnitude smaller than the annual commercial catch, and thus the actual number of fish is likely to be several orders of magnitude greater than the effective population size (43). Low N_e/N ratios thus appear to be characteristic for highly fecund species with high juvenile mortality, and not only are of interest in the conservation of genetic resources but also may provide powerful insights into spawning ecology and recruitment of marine species.

Implications.

Is there any adaptive significance to the reduction in genetic diversity demonstrated here? Existing evidence from computer simulations and laboratory studies suggests a complex relationship between molecular and adaptive genetic variability, primarily attributable to the presumed neutrality of molecular markers, contrasting mutation rates, the polygenic control of adaptive traits and the effects of dominance and epistasis (44). The microsatellite data presented here showed, however, that the effective size of the Tasman Bay snapper population was sufficiently small to cause loss of alleles at neutral and weakly selected genes, which nevertheless may be potentially adaptive in different environments. Such alleles may not contribute significantly to extant quantitative genetic variation, but may be crucial for the long-term adaptive potential of a population under changing environmental conditions. Recent assertions of global warming causing recruitment failure in cold-adapted North Sea cod (45) emphasize the importance of maintaining the adaptive potential of exploited populations. A widely publicized rule of thumb for minimum effective population sizes required to maintain genetic diversity is 50 individuals for short-term conservation of heterozygosity and 500 for more long-term considerations of adaptability (46). Using the N̂_e/N̂ estimate of 10⁻⁵ in snapper, this translates into census population sizes of 5 million and 50 million individuals, respectively. Therefore, fish stocks of several million individuals may be in danger of losing genetic variability in the long term, and so genetic diversity should become a management consideration in many marine exploited species. Considering that more than half of all marine fisheries are based on fully exploited or overexploited stocks, fishing may have already caused a considerable loss of overall biodiversity.

In addition to such genetic concerns, the low N_e/N ratio suggests that only very few fish contribute successfully to the next generation, possibly in part explaining the often poor relationship between the size of the spawning stock and recruitment (47). The recruitment processes suggested by genetic data also open the exciting possibility of identifying the demographic section of the population most likely to reproduce successfully and to protect these individuals from excessive exploitation. A close collaboration between molecular geneticists and fisheries biologists would be required to carry out research into recruitment processes of marine populations and their possible implications for fisheries management and conservation.