Identification of the binding sites of regulatory proteins in bacterial genomes

Abstract

We present an algorithm that extracts the binding sites (represented by position-specific weight matrices) for many different transcription factors from the regulatory regions of a genome, without the need for delineating groups of coregulated genes. The algorithm uses the fact that many DNA-binding proteins in bacteria bind to a bipartite motif with two short segments more conserved than the intervening region. It identifies all statistically significant patterns of the form W₁N_xW₂, where W₁ and W₂ are two short oligonucleotides separated by x arbitrary bases, and groups them into clusters of similar patterns. These clusters are then used to derive quantitative recognition profiles of putative regulatory proteins. For a given cluster, the algorithm finds the matching sequences plus the flanking regions in the genome and performs a multiple sequence alignment to derive position-specific weight matrices. We have analyzed the Escherichia coli genome with this algorithm and found ≈1,500 significant patterns, which give rise to ≈160 distinct position-specific weight matrices. A fraction of these matrices match the binding sites of one-third of the ≈60 characterized transcription factors with high statistical significance. Many of the remaining matrices are likely to describe binding sites and regulons of uncharacterized transcription factors. The significance of these matrices was evaluated by their specificity, the location of the predicted sites, and the biological functions of the corresponding regulons, allowing us to suggest putative regulatory functions. The algorithm is efficient for analyzing newly sequenced bacterial genomes for which little is known about transcriptional regulation.

As more and more genomes are sequenced, organisms are increasingly represented by a list of genes; however, there is little knowledge as to how these genes are regulated. Even for Escherichia coli, the best understood bacteria, only about one-fifth of the estimated 300–350 regulatory proteins (1) have characterized binding sites. For newly sequenced bacteria, only those transcription factor-binding sites that happen to match those already identified in E. coli or Bacillus subtilis can be used to infer regulatory properties of the organism. Consequently, it is clearly important to develop genome-wide computational tools to identify the binding sites of uncharacterized transcription factors. That new bacteria are sequenced almost weekly indicates that developing these computational tools is a high priority.

One commonly used approach to identify transcription factor-binding sites is to delineate a group of coregulated genes [e.g., by clustering genes on the basis of their expression profiles (2, 3), or functional annotation] and search for common sequence patterns in their upstream regulatory regions. An alternative approach is to compare the regulatory regions of orthologous genes in different species to identify functionally conserved sequence motifs (4–6). These approaches have been successfully used to analyze bacterial genomes, but they both have limitations. For example, clustering genes on the basis of their expression profiles is far from an exact and objective process; each gene set defines a particular context, and searching for all contingencies to which the cell can respond is daunting. Furthermore, observed expression patterns can result from a regulatory cascade or from multiple factors acting simultaneously, increasing the difficulty of identifying all of the relevant sites. Interspecies comparison is limited by the availability of species separated by proper evolutionary distances. In addition, multiple alignment algorithms do not yet respect the phylogenetic relationships. Finally, when the conserved sequence elements are identified, it is a challenging task to group the potential sites for each gene into regulons (7).

The computational algorithms used to extract common sites from a select group of genes can be categorized as either direct search, i.e., count all sites in a certain class (8–10), or relaxational, i.e., guess a pattern and improve it iteratively (11–14). The computational effort in the former approach grows exponentially in the length of the site but nothing is missed, whereas the latter can find longer and more diffuse patterns but may not converge to the global optimal. Algorithms also differ in how they assess the statistical significance of a motif: either extrinsically, by contrasting the frequency of the motif in the gene cluster with that in the rest of the genome (8); or intrinsically, by determining how much the number of occurrences of the motif deviates from that expected by chance (e.g., given the single base frequencies in the cluster). Applications to entire genomes are difficult because of the quantity of data involved, the absence of suitable comparisons for the extrinsic methods, the multiplicity of patterns, and the limitations of simple background models for the probabilities. Some of these limitations were overcome with the Mobydick algorithm (15), which searches for multiple motifs in parallel by sequence segmentation. It was run successfully on the regulatory sequences upstream of all the genes in yeast. However, it does not allow for the discovery of new position-specific weight matrices (PSWM; related to a table of the number of bases at each position for aligned sites), which is the most fruitful way of describing bacterial regulatory sites.

Transcription factor-binding sites in bacterial genomes are usually long, ≈30 bases, and variable. However, often most of their sequence signal is carried in two conserved subregions, each about 6 bases in length (16), which contain the predominant contacts with the transcription factor. This bipartite character results from the fact that most prokaryotic transcription factors have two DNA-binding regions, because of either dimerization of the transcription factor or the presence of two DNA-binding domains in a single protein as in the case of σ factors (17). A number of researchers have exploited this fact to search for patterns of the form W₁N_xW₂ (henceforth termed dimers), where W_1,2 are short oligonucleotides (henceforth called words) separated by x arbitrary bases (9, 10, 15, 18, 19).

In this paper, we develop a new dimer-based algorithm that generates PSWMs and puts an intrinsic probabilistic score on the resulting motifs. When applied to E. coli, we identify the binding sites of one-third of the characterized transcription factors with high statistical significance. In addition, this algorithm predicts binding sites for many uncharacterized transcription factors that potentially define new regulons. We evaluate the significance of these predictions from their probability score, their positional distribution, and the coherence of the biological function of the putative group of coregulated genes. Our success in applying this algorithm to E. coli suggests it will be useful in identifying regulatory networks of newly sequenced genomes.

Methods

Our algorithm consists of three steps. In the first step, it tabulates the positions of all strings W up to some length (typically 5 for ≈1 Mb of sequence) in the data. This table is then searched to count the number of occurrences of the dimer W₁N_xW₂, where the spacing x varies typically from 0 to 30 bp. This number is compared with that expected if W_1,2 are uncorrelated, and Poisson statistics is used to assign a probability to the observation. The second step takes all statistically significant dimers and clusters them on the basis of sequence similarity. The final step takes the actual genomic sequences matched by any member of a cluster plus the flanking regions (with no double counting) and performs a multiple sequence alignment to yield the PSWM. To search for putative sites, standard information theory measures are used to score sequences using PSWMs.

The computer time in step 1 scales as N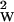 + L, where N_W is the number of words and L is the total length of data. For 10³ words and a megabase of data, the calculation can be done in 30 min on a Silicon Graphics (Mountain View, CA) work station. Typically L ∼ N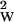, because going to longer words would reduce the dimer counts to below the order of one. For step 2, we have to compare all significant dimers with each other, which for typical bacterial data can be done by the simplest pairwise alignment algorithm in about as much time as step 1.

To calculate the probability of observing n(D) copies of a dimer D by chance, we calculate its expected value from the formula,

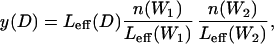1

where n(W₁) and n(W₂) are the total number of occurrences of W₁ and W₂ in the data set and L_eff(M) = ∑_r(L(r) − L(M) + 1) is the number of independent positions in the data where a motif M of length L(M) can be placed (M can be W₁, W₂, or D). The summation is over the regulatory regions of all the genes (e.g., the upstream regions of all the operons in E. coli), each with a length L(r).

A P value is assigned to a dimer assuming that the background distribution is Poisson:

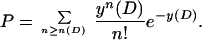2

A dimer is considered significant if P < 1/N_dimer, where N_dimer is the total number of dimer patterns examined. When either W₁ equals W₂ (direct repeat) or its reverse complement (palindromic), the cutoff on P is set by the number of repeated or palindromic dimers. These cutoffs ensure that the total number of false positives is of order one if the data are described by the background model.

Many patterns found in step 1 are similar and represent different (typically overlapping) versions of the conserved core of the binding sites of the same factor. For example, the following two dimer patterns are related to the binding sites of LexA in E. coli:

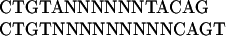To divide the significant dimer patterns we found in step 1 into distinct groups, we first score the best alignment for each pair of dimers as illustrated above. The score is the number of matches minus the number of mismatches, and matches of N to any other base or overhangs (e.g., the terminal T in the second sequence) are ignored. We then create a similarity score between zero and one by normalizing the pair scores by the maximum over all possible pairs and then cluster the dimers by using the CAST algorithm developed by Ben-Dor et al. (20). We experimented with various thresholds for the cluster score (the average of all the pair scores of its members) and found that a threshold of 0.6 gave good compact clusters.

A cluster obtained in step 2 will give us only the most conserved part of the binding sites of a putative factor but provides no information about the middle or the flanking regions. However, this information still resides in the genomic sequence. For a given cluster, we extract the actual sequences that are matched by any member of the cluster plus about 10 flanking base pairs. We then perform a multiple sequence alignment by using Consensus (11), which easily finds the correct alignment because the extracted sequences are short and contain a strong pattern. Thus for each cluster, we derive an alignment matrix, n_iα, which specifies the number of nucleotides of base α at position i of the putative binding site. Such an alignment matrix quantitates the preferences of the bases for the putative DNA-binding factor.

Given an alignment matrix n_iα, we use it to derive the PSWM, w_i,α, and to score potential binding sites on the basis of a scheme used by the consensus algorithm (11). The alignment matrix is converted to a frequency matrix f_i,α = (n_iα + 1)/∑_α(n_i,α + 1), with a pseudo count added because of the Baysian estimate. The frequency matrix is then used to calculate a PSWM w_i,α = log(f_i,α/f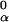), where f 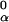is the background frequency of base α (for E. coli upstream regions 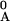f ≈ f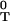 ≈ 0.3). The score of a sequence s₁s₂ … s_L of length L (equal to the width of the matrix) is given by S = ∑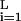w_i,si and correlates with the binding affinity of the protein factor to the DNA sequence (21). When the PSWM is used to score all the distinct length L pieces from a data set, the histogram of the scores can usually be approximated by a Gaussian. Hence, we can characterize a set of aligned sequences and its associated PSWM by the mean m_s and rms score δ_s of the defining data and the corresponding scores against the background sequences, m and δ. The more separated the two distributions are, the better the PSWM can distinguish potential sites from background sequences. A quantitative measure of the specificity of the PSWM is the conventional z score, z = (m_s − m)/δ.

The sites predicted by a PSWM are those with a score larger than a cutoff S₀. The distance between the cutoff S₀ and the mean background score m measured in units of the background rms score, (S₀ − m)/δ, gives the false-positive rate. (The score difference in units of δ can be converted directly into a probability assuming a Gaussian distribution.) On the other hand, (m_s − S₀)/δ_s controls the false-negative rate; the smaller S₀, the less likely a true binding site will be missed. Thus the choice for the cutoff depends on the tradeoff between false-positive and false-negative rate. Setting S₀ = m_s gives a 50% false-negative rate if the distributions of the scores of the defining sequences are symmetric around the mean, with a false-positive rate determined by the z score.

The positional and functional analysis of matrix predictions was performed by using flat files containing known and predicted promoters from Regulon DB (22) (http://kinich.cifn.unam.mx:8850/db/regulondb_intro.frameset), annotated E. coli K-12 MG1655 genome sequence from the National Center for Biotechnology Information, and gene multifunctional classification from GenProtEC (23) (http://genprotec.mbl.edu/).

Results

Deriving PSWMs from Overrepresented Dimer Patterns.

We used our algorithm to identify all statistically significant dimers in the noncoding regions upstream of all ≈2,500 documented or predicted transcription units in E. coli (24) (http://tula.cifn.unam.mx/∼madisonp/E.coli-predictions.html). Because almost all known transcription factor-binding sites occur within 300 nt upstream of the start point of translation (25), we limited our search to this window. We identified 1,775 statistically significant dimers, W₁N_xW₂, where each word was 3–5 nt in length. Among these dimers, 261 are direct repeats (W₁ is the same as W₂), and 748 are palindromic (W₁ is the reverse complement of W₂). After poly A/T patterns (which are abundant and nonspecific) were filtered out, the remaining 1,554 dimers were grouped into 849 clusters, of which 233 clusters contained 2 or more dimer patterns (the largest cluster having 61 dimers), and 616 clusters contained a single dimer pattern.

The dimer clusters were then used to obtain additional sequence information for the putative binding sites in the genome to derive PSWMs. To illustrate the process, we consider a dimer cluster matching the binding sites of LexA. The dimers in the cluster all share the palindromic CTGN₁₀CAG motif observed in almost all the experimentally determined binding sites of LexA. Table 1 shows the alignment matrix derived from the sequences taken from the 77 upstream positions that matched the dimers in the cluster. The alignment of the extracted sequences provides additional information not present in the original dimer cluster. For example, the middle regions have some A/T preference, with some positions exhibiting a strong bias of A over T or vice versa (e.g., position 5 adjacent to the conserved CTG core is predominantly T). Alignment matrices derived from each cluster were numbered and converted to PSWMs to score potential binding sites in the genome (see Methods for a detailed description of this process). All of the matrices and their associated statistics are given in the supplementary materials.

Table 1.

The alignment matrix derived from the LexA cluster

A	37	0	0	0	7	34	15	36	21	29	20	33	25	39	0	76	1	10
C	10	76	0	1	4	11	12	11	17	16	14	15	12	12	77	1	0	11
G	13	0	0	76	9	9	12	15	8	10	9	10	12	10	0	0	76	19
T	17	1	77	0	57	23	38	15	31	22	34	19	28	16	0	0	0	37

Different columns give the number of counts for the four bases at different positions in the multiple sequence alignment. For the positions where a single base represents the consensus (26), the corresponding counts for the dominant base are shown in bold face. 

PSWMs That Identify Known Transcription Factor-Binding Sites.

To determine whether our PSWMs match the recognition profile of any known E. coli transcription factor, we tested their ability to identify experimentally determined binding sites of 59 different transcription factors in a database assembled by Robison et al. (16) (http://arep.med.harvard.edu/). Each PSWM was used to score all the subsequences of each site, and scores greater than both thresholds m_s − 2δ_s, m + 2.5δ were considered to be positive hits. The cutoff of m_s − 2δ_s enabled most of the defining sites to be identified, whereas the cutoff of m + 2.5δ ensured a low false-positive rate of less than 0.6%. To allow partial overlaps between sites predicted by the matrix and the known sites, we appended 5 bases (drawn at random by using the background frequencies) to the two ends of the known sites and used the matrix to score all the subsequences of the extended sites. The significance of each matrix positively identifying sites for a particular transcription factor was then calculated by using the expected number of hits by chance and the observed number of hits to derive a probability score (P), assuming a Poisson distribution. We found that the binding sites of 37 transcription factors match at least one of our matrices with high statistical significance (i.e., a P value of less than 1/N_factorsN_matrices, or −log₁₀P > 4.76); the most significant top 20 matches are listed in Table 2, together with the statistical significance of the match and the specificity of the matrix as measured by its z score.

Table 2.

Transcription factors whose known binding sites were matched significantly by one of the matrices

Factor	Sites	Hits	Expect	Sig	Rbias	z score	Consensus	Consensus (known)
crp (001)	49	23	0.08	47.7	53.1	4.64	TGTGAN6TCACANWW	WWNTGTGAN6TCACANWW
lexA (005)	19	19	0.09	37.2	3.81	4.42	CTGTN8ACAG	TACTGTATATAHAWMCAGYA
tyrR (058)	17	15	0.42	17.8	9.80	4.25	TGTAAANWN4TWTACA	RTGTAAWNWWATNTTTACANM
fnr (103)	14	11	0.13	17.4	4.72	4.20	TGAN6TCAAW	AAWTTGATNWMNATCAAWWWW
argR (469)	17	19	1.27	15.6	2.57	3.62	TGATTAWNAATCAWNHTNA	WNTGAATAAWWATNCANW
cpxR (774)	12	13	0.45	14.5	1.27	3.88	TNNCAAAAGNNGNVRAAAAGS	GYAAAN5GTAAR
rpoN (061)	6	6	0.02	13.1	2.36	4.80	AANNCTGGCAN6TTGCW
narL (107)	11	10	0.34	11.3	0.89	3.84	CCCATMNNTN5TGGGN4AK	TWMYYCNNWAKGGGTA
cysB (444)	3	6	0.05	10.7	1.90	4.48	GGGN10CCC
phoB (712)	15	7	0.13	9.92	6.49	3.99	TGTN8TGT	CTGTCATAWAWCTGTMAYMWWH
fruR (404)	12	9	0.52	8.30	0.36	3.45	TSMVWHGCTGAMAGCTKTCAGC	GCTGAAWCGNTTCANY
arcA (722)	14	5	0.08	7.68	3.63	3.91	TGTN9GTT	GTTAAYTAWAWKTWA
metJ3 (028)	10	11	1.18	7.27	1.58	4.15	TNGCGTACWHNTGTACGC	RKACRTCTRRACRTCTRRACGTMT
flhCD (057)	3	5	0.10	7.12	0.52	4.68	SCCGGN7CCGGC
purR (419)	22	10	1.07	6.70	0.26	4.36	DNGCAGRMAN4WNNTMWTNCTGGA	ANGMAAACGTTTNCGTK
rpoD18 (742)	34	5	0.13	6.59	0.55	4.62	CGGN7CCG	TTGAYAN18TANA
soxS (027)	14	7	0.43	6.44	0.56	4.69	WNNWGCCGGNKWN3CCGGC	KNNANNGCAYNDWN5AWNYNMWN3M
argR2 (785)	7	5	0.15	6.24	12.2	3.96	ATAWN8AATA
rpoH2 (704)	7	4	0.07	6.15	2.52	4.59	CCCN9GGG
oxyR (454)	4	4	0.07	6.11	0.55	4.30	TCGN7CGA

Column 1: the name of the factor; the number in the bracket is the ID of the matrix. Column 2: number of experimentally determined binding sites for the factor. Columns 3–5: number of positive hits by the matrix, expected number of hits based on background distribution, statistical significance of the match given by −log₁₀P. Columns 6–9: noncoding bias ratio, z score, consensus of the matrix, consensus from known sites (only factors with more than 10 known sites are shown). 

In a number of cases, several matrices matched the same factor (e.g., CRP). Typically, the matrices describe slightly different but overlapping sequences; however, the corresponding dimers did not have enough sequence overlap to enable them to all be clustered together. In such cases, only the matching matrix that contains the most significantly overrepresented dimer is displayed in Table 2. For a few transcription factors, the number of positive hits by a particular matrix exceeds the number of known sites, because more than one subsequence in the binding site scored above the cutoff threshold.

We compared the consensus sequences deduced from our alignment matrices with those for the known transcription factors (deduced from the experimentally determined binding sites) in those cases where enough sites were known to give a reasonable consensus [the consensus sequences were derived by using the convention of Cavener (26)]. In many cases, our consensus closely resembles that from the known binding sites (e.g., CRP and LexA; see Table 2). However, in some cases, the consensus sequences differ (e.g., SoxS and RpoD). In these instances, the matrix is identifying a pattern shared only in a subset of the known sites. For example, matrix 742 is clearly not describing known RpoD promoter sequences, yet the matrix is highly specific (see Table 2 for its z score). We surmise that matrix 742 is identifying the binding sites of some other factor that overlaps with some RpoD promoters.

PSWMs That Predict Regulons of Uncharacterized Transcription Factors.

A significant number of the matrices that we derived did not match the binding-site profiles of any known transcription factors in the previous test; we termed these “new matrices.” To eliminate redundancies among these matrices, we defined a similarity score between pairs of matrices by using one matrix to score the sequences defining the other. Matrices for which the probability of the score was less than 1/N_pair (where N_pair is the number of matrix pairs) were linked. We clustered the matrices by single linkage and selected as a representative the one that was derived from the largest dimer cluster (simply merging the clusters together did not improve the quality of the profiles, because some highly nonspecific dimers have a large number of false-positive matches that would dominate each profile). By this method, we obtained 122 distinct new matrices. Because the binding sites of only a small fraction of the 300–350 transcription factors in E. coli are known, it is likely that some of the new matrices describe the binding sites of the uncharacterized factors.

It is expected that some of the new matrices will be more successful than others in predicting binding sites; consequently, it is important to identify properties of the matrices that correlate with biologically relevant predictions, which will enable further analysis to be prioritized by rank ordering the matrices using these properties. We assessed the biological relevance of the predictions of the new matrices by determining whether the properties of each matrix are similar to the following diagnostic features of known transcription factor binding sites: (i) that the binding sites occur preferentially in the noncoding regions; (ii) that the binding sites are localized at preferred positions with respect to the transcription start point (TSP); (iii) that the regulons are composed of genes with coherent biological functions. In all of these tests, we examined the high scoring (score higher than m_s), thus more specific predictions by each matrix.

To quantitate the noncoding vs. coding bias of the predictions made by a matrix, we counted the number of sites predicted in all the noncoding vs. coding sequences in the genome. We then calculated the ratio, R_bias, of the density of predicted sites (number of sites per base) in the noncoding region to that in the coding region. We also calculated a P value for the bias based on Poisson distribution by using the density in the coding region to define the expected number in the noncoding region. For the 37 matrices matching known sites, 22 of them were significantly biased toward the noncoding region, with a P value of bias smaller than 10⁻⁵. Table 2 lists the R_bias values for the top 20 matrices matching known sites; in most cases, the predicted sites are biased toward noncoding sequences. The same calculation was also performed for all of the 122 representative new matrices; some of the results are listed in Table 3.

Table 3.

A list of new matrices and their properties

ID	z score	Rbias	Pfunc	Subcategory
223	3.76	4.59	0.0002	Primary active transporters
092	4.16	5.40	0.0004	Carbon utilization
015	4.15	11.76	0.0010	Membrane
072	4.49	1.84	0.0012	Transposon related
155	4.18	1.17	0.0015	Cell division
613	3.73	1.21	0.0016	Plasmid related
023	4.78	1.78	0.0017	DNA related
472	3.66	1.17	0.0018	Cell division
770	3.91	2.19	0.0021	Energy metabolism, carbon
011	7.01	84.48	0.0022	Capsule (M and K antigens)
393	3.73	1.10	0.0031	Pilus
013	4.58	3.22	0.0032	Transposon related
142	3.92	3.54	0.0034	Prophage genes
081	4.21	1.08	0.0037	Energy production/transport
602	4.11	1.36	0.0048	Colicin related
349	3.49	1.14	0.0059	Central intermediary metabolism
362	3.48	1.15	0.0065	Metabolism of other compounds
499	3.81	1.10	0.0077	Type of regulation
048	4.51	4.16	0.0095	Genetic unit regulated
317	3.36	1.32	0.0097	Pilus
510	3.90	1.72	0.0100	Prophage genes
373	3.67	1.58	0.0147	Pilus
278	3.11	2.16	0.0168	Primary active transporters

Columns 1–5: the ID of the matrix, the z score, the noncoding bias ratio, the smallest P value for the functional overrepresentation (by which the table is ordered), and the corresponding functional subcategory. 

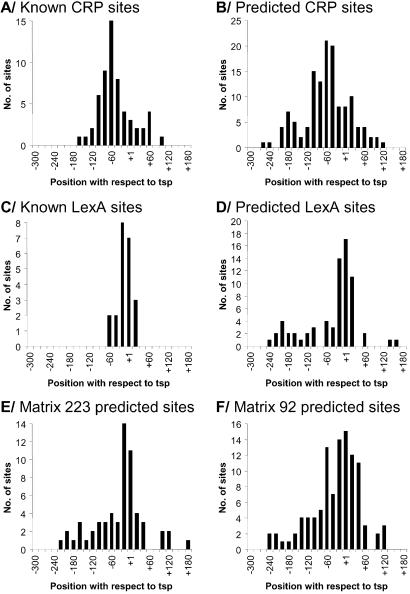
The binding sites of characterized transcription factors often have preferred positions with respect to the TSP. For example, activators typically bind upstream of the core promoter element. A well known case is the binding sites of the global activator, CRP, which have strong preferences for positions centered between 40 and 90 bases upstream of the TSP (Fig. 1A). In contrast, repressors such as LexA predominantly function by binding to target sites overlapping the core promoter elements to block the binding of RNA polymerase (Fig. 1C) or by binding downstream of the TSP to disrupt efficient transcription elongation. Thus sites predicted by a matrix that have a preferred positional distribution with respect to the TSP supply additional evidence that they may have a regulatory function.

Figure 1.

Distribution of the center positions of the predicted binding sites (relative to the transcriptional start point) for four weight matrices. For the two matrices matching CRP and LexA, positional distribution of the known binding sites is also shown.

We analyzed the positional distribution of sites predicted by matrices in the 300-nt windows upstream of the ≈2,500 transcription units relative to the TSP by using the known and predicted promoter positions listed in the Regulon database (22). It is clear that for the two matrices matching CRP and LexA, the positional distribution of the predicted sites is very similar to that of the known sites, with peaks at similar positions (Fig. 1 B and D). Interestingly, the distributions of the predicted sites for both CRP and LexA also have a second peak further upstream ≈200 nucleotides from the TSP. This is not due to the sites regulating divergently transcribed genes, because in these cases the predicted sites were assigned to the nearest promoter. These sites may play a subtle modulatory role and therefore are less likely to have been identified experimentally. Examples of the positional distribution of predicted sites are shown for two new matrices, matrices 223 and 92 (Fig. 1 E and F, respectively). In each case, there is a large peak in the positional distribution downstream of the core-binding site, suggesting that the factors are likely to function as repressors. Many new matrices exhibit highly clustered distributions of sites with respect to the TSP (data not shown), suggesting that they are functional predictions. However, other matrices exhibit little or no bias in the distribution of their predicted sites; in these instances, too little is known about the properties of transcription factors at a global scale to conclude whether these sites are functional.

To suggest possible regulatory functions associated with the new matrices, we analyzed the biological functions of the transcription units downstream of the predicted sites by using information provided in GenProtEC database (23). This database classifies E. coli genes into one or more functional categories on the basis of their cellular function; the categories are hierarchically organized into 10 major functional categories at the top level that expand in to 49 different subcategories. For a given matrix, we tested whether the potentially regulated transcription units were overrepresented in any subcategories, given the known number of operons in that particular category for the entire genome. We then calculated a P value for the degree of overrepresentation in each subcategory. This approach was validated by the results from analyzing known matrices; many of them predicted regulated transcription units that were significantly overrepresented in specific subcategories, with functions consistent with the current knowledge about that factor. For example, matrix 1, which matched CRP sites, predicts transcription units most overrepresented in the subcategory “metabolism/carbon utilization” with a P value 5 × 10⁻⁷, and matrix 5 (matching LexA) was most overrepresented for the subcategory “information transfer/DNA related” with a P value smaller than 10⁻¹⁴. We performed the analysis for all 122 representative new matrices, and each was assigned a subcategory corresponding to the most overrepresented one (i.e., having the smallest P value, denoted by P_func). Examples are listed in Table 3.

We found that there is a general correlation between the intrinsic statistics of each matrix and its functional characterization. For example, matrices with high specificity also tend to have high maximum dimer significance, a large noncoding bias and small P_func (i.e., matrices with high specificity tend to predict transcription units with coherent functions; see http://mobydick.ucsf.edu/∼haoli/ecoli.html). Table 3 lists a subset of the new matrices that have reasonable specificity (z score > 3.0), some bias toward noncoding region (R_bias > 1.0), and are overrepresented in certain subcategories (P_func < 0.02). These matrices are good candidates for further experimental tests. A complete list of the parameters for all 122 new matrices, as well as their predicted transcription units, is provided (see http://mobydick.ucsf.edu/∼haoli/ecoli.html).

Discussion

We have developed an algorithm that is capable of identifying a significant fraction of the regulatory sites in a bacterial genome by using only sequence information and annotated open reading frames. Built on the simple observation that many DNA-binding proteins in bacteria bind to a bipartite motif with two short segments that are more conserved than the region separating them, the algorithm finds all statistically significant patterns of that form. It then refines the description by clustering the patterns, identifying the matching sequences in the genome, and performing multiple sequence alignment to derive PSWMs. The algorithm is simple and effective computationally and takes less than ½ hour to exhaustively search all the dimer patterns in the E. coli upstream regulatory regions on a SGI workstation.

Prior work that searches for gapped patterns has not used our particular assignment of probabilities and clustering. Vanet et al. (10) filtered dimer patterns on the basis of preassigned values for their number of occurrences, and probabilities were assigned by shuffling data. Their algorithm did not identify CRP sites or sites for other prominent E. coli transcription factors. Sinha and Tompa (9) computed probabilities by comparison to a third-order Markov model and gave predictions for yeast gene clusters (derived from known functional pathways and gene expression data), most of them quite small. Many of their predictions were found by searching the entire genome (15). van Helden et al. (18, 19) used an approach similar to ours to detect dimer patterns, but they restricted the analysis to small clusters of coregulated genes, thus typically only a few distinct patterns were found per gene cluster. They did not attempt to cluster dimer patterns and derive PSWMs. Our results might be contrasted with McGuire et al. (6), where they used Gibbs sampling to search known regulons for known sites (their control) and then used homologues of the E. coli regulons in other organisms, either alone to find new sites or grouped with the E. coli upstream regions to enhance the signal for common sites. With their control set at a reasonable false-positive rate (see their table 1), they get 15–20 of the strongest factor sites, a result comparable to ours that we obtained without using any prior knowledge of regulons (Table 2). van Nimwegen et al. (7) clustered the interspecies data of McCue et al. and Rajewsky et al. (4, 5) into regulons. By using only sites from E. coli, their algorithm performed less well than our algorithm, since less information about the structure of the binding site was used. When all the species were retained, 50–100 new regulons were predicted, typically smaller than those described here.

The binding sites of several well known transcription factors were not identified by our algorithm. For example, no dimers were identified that truly represented RpoD promoter sites. The information content (thus the specificity) of the RpoD sites is similar to that of the CRP sites (which were easily identified) but distributed over a longer sequence, leading to fuzziness in the two core sites. For example, the consensus for RpoD with an 18-bp spacer from the known sites is TTGAYAN₁₈TANA, with the second core TANA barely identifiable. Our algorithm also missed the binding sites of the AraC family of transcription factors. For example, the dimer pattern AGCAN₈CATAA representing AraC sites was overrepresented, with a significance of −log₁₀P = 4.16 (if the occurrences of the asymmetric site in both orientations were considered). However, this was still below the cutoff threshold of 6 we set to control false positives.

As more and more DNA microarray data become available, it is possible to combine the predicted motifs proposed here with genome-wide mRNA expression data to identify conditions under which the motifs may play a regulatory role. For example, Courcelle et al. (27) identified 42 LexA-dependent transcriptional units by comparing the response to UV irradiation of wild-type cells with those containing a LexA mutant. Our matrix 5 predicted a total of 64 transcripts, of which 19 coincided with those found by Courcelle et al. (only 1 was expected by chance). In another example, from 16 NtrC-dependent transcriptional units identified by Zimmer et al. (28), matrix 52 predicted 6 out of 54 total predictions (expectation 0.3). Thus, we can confidently assign functions to matrices 5 and 52. Once expression data for cells under diverse conditions become available, it will be informative to systematically match regulons predicted by the matrices with those defined experimentally in various contexts to gain insight into the global organization of the transcriptional program in E. coli.

Our algorithm is straightforward to apply to other sequenced bacterial genomes. A preliminary study of B. subtilis revealed ≈1,700 dimers, a number comparable to that found in E. coli. In contrast to E. coli, the primary σ site in B. subtilis was easily obtained, suggesting a greater degree of conservation of σ sites in B. subtilis compared to E. coli (M. Mwangi and E.D.S., unpublished work). Our approach should be particularly powerful when applied to genomes of relatively unstudied bacteria. Our studies in E. coli have demonstrated that PSWMs with excellent intrinsic statistics predict transcription factor-binding sites and their regulons with a high degree of confidence. Thus, such an analysis can be applied to obtain a preliminary blueprint of the transcriptional networks in these bacteria.

We have posed the full data set from analyzing E. coli genome on our web site (http://mobydick.ucsf.edu/∼haoli/ecoli.html) and invite biologists to do further analysis and perform experimental tests.

Abbreviations

PSWM

position-specific weight matrices

TSP

transcription start point