Friction traced to the single atom

Abstract

Friction is caused by dissipative lateral forces that act between macroscopic objects. An improved understanding of friction is therefore expected from measurements of dissipative lateral forces acting between individual atoms. Here we establish atomic resolution of both conservative and dissipative forces by lateral force microscopy, presenting the resolution of atomic defects. The interaction between a single-tip atom that is oscillated parallel to an Si(111)-(7 × 7) surface is measured. A dissipation energy of up to 4 eV per oscillation cycle is found. The dissipation is explained by a “plucking action of one atom on to the other” as described by G. A. Tomlinson in 1929 [Tomlinson, G. A. (1929) Phil. Mag. 7, 905–939].

Ultimately, friction between macroscopic objects is caused by nonconservative force components between single atoms, as recognized by Tomlinson (1) more than 70 years ago. Friction studies have benefited greatly from the invention of the lateral force microscope, introduced in 1987 (2). The resolution power of the lateral force microscope has been improving steadily, opening many applications in high-resolution tribology studies (3–6) including the study of chemical phase separations (7). However, the observation of single atomic defects—the touchstone of atomic resolution—has not been achieved by lateral force microscopy yet. Already atomic force microscopy (AFM) (8) by normal forces has faced severe challenges (9) that caused a delay of almost a decade on the road to atomic resolution on reactive materials (10). The solution to these challenges was the utilization of the frequency-modulation (FM)-AFM technique (11), in which a cantilever with a spring constant of k ≅ 20 N/m is subject to positive feedback such that it oscillates with a constant amplitude of A ≅ 10 nm (10). The cantilevers resonance frequency is determined by its effective mass, its spring constant, and the average stiffness of the bond between tip and sample. The frequency shift is used as the feedback signal (10). The dissipated power between tip and sample is measured as the difference between the power required for maintaining a constant amplitude when the cantilever is close to the sample and the power required when the cantilever is far away from the sample (12, 13).

The challenges faced by lateral force microscopy are similar to those faced by normal force microscopy, and therefore FM-AFM appears to be the natural choice for pursuing atomic resolution in lateral force microscopy (14). Unfortunately, the large amplitudes required by classic FM-AFM are prohibitive for lateral force microscopy, because atomic resolution is not achievable with cantilevers oscillating over some 10 nm parallel to a surface (14). However, our group has recently established FM-AFM operation with subnanometer amplitudes (15) by using stiff cantilevers with k ≅ 2,000 N/m (16). It was found also that the use of very small amplitudes enhances the sensitivity to atomic dissipation channels (17). Using stiff cantilevers and small amplitudes improves resolution (15) and facilitates lateral force detection.

In the following, a description of the measurement technique and the lateral force sensor for true atomic-resolution lateral force microscopy is given followed by a discussion of the relation between the conservative and dissipative force components and the experimental observables. Experimental results showing atomically resolved lateral forces atomic defects are presented, and finally, a theoretical explanation is given.

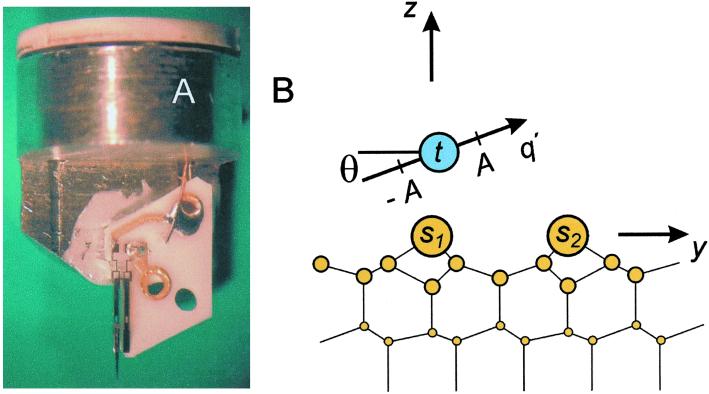
Fig. 1A shows the force sensor used in the experiments: a quartz tuning fork is used as a single quartz cantilever (“qPlus” configuration) (16). This setup is a realization of Tomlinson's Gedanken experiment from 1929 (1). In the lateral force sensor, the tip is mounted parallel to the tuning-fork prong and oscillates nearly parallel to the surface with an amplitude A. The quartz tuning forks used (DS 26-quartz crystal, Swiss Micro Crystal, Grenchen, Switzerland) have a spring constant of k′ = 1,800 N/m, an eigenfrequency of f′₀ = 32,768 Hz, and a quality factor of about Q′ ≈ 50,000. In the assembled sensor shown in Fig. 1A, one prong is attached to an alumina substrate, and a tungsten tip is mounted to the other prong. The effective length of the cantilever is increased by the tungsten tip, the spring constant decreases to k = 1,350 N/m, the mass of this tip results in a lower eigenfrequency of f₀ = 10,214 Hz, and the dissipation in the mount of the fixed prong involves a drop of the quality factor to Q = 1,180. The sensor is attached to an actuator, and the oscillation is sustained by vibrating the actuator with an amplitude A_drive. An electronic circuit (9) controls a constant-amplitude oscillation of the sensor. The phase difference between the excursions of actuator and cantilever is adjusted to ϕ = +90° so that the cantilever oscillates at frequency f₀. The energy dissipation of the cantilever is accessible through an output terminal g ∝ A_drive/A of the oscillator control electronics. For constant amplitudes, g is proportional to the total energy loss of the cantilever per oscillation cycle (13), and an increased energy dissipation in the tip-sample interaction is reflected in an increased value of g. The oscillation frequency is analyzed with a commercial quartz stabilized phase-locked-loop detector (Nanosurf AG, Liestal, Switzerland).

Fig 1.

(A) Lateral force sensor consisting of a tuning fork with one fixed prong and a tip attached to the free prong. (B) Geometry of tip atom t and sample atoms s₁ and s₂. The tip oscillates along an axis that is tilted by an angle θ (¦θ¦ ≤ 10°) with respect to the y axis.

The ideal test surface for the atomic study of lateral forces should have two properties: widely spaced top-layer atoms and a strong short-range interaction between the probe tip and the sample atoms. The Si(111)-(7 × 7) surface fulfills these demands, because its surface atoms (adatoms) are spaced by a distance of at least 6.7 Å, and the adatoms interact strongly with the AFM tip (18). Fig. 1B illustrates the geometry of the tip-sample interaction: the front atom t of the oscillating tip interacts with two sample atoms s₁ and s₂. The tip oscillates with an amplitude A around its average position. The tip motion is essentially parallel to the surface with a small tilt angle θ with respect to the y direction. For θ = 0, the amplitude has to be smaller than about a quarter of the next neighbor distance of the surface atoms. For larger amplitudes and θ = 0, several surface atoms interact strongly with the tip over one oscillation cycle, thereby distorting the images so that the interpretation of the data becomes difficult. For tilt angles |θ| ≈ 6° this problem is solved, and larger amplitudes can be used without the presence of convolution effects.

The tip-sample interaction is reflected in three physical observables. A tunneling current flows if a bias voltage is applied between electrically conductive tips and samples, enabling dynamic scanning tunneling microscopy with a rapidly oscillating tip. The conservative part of the tip-sample forces results in a frequency shift of the cantilever. The nonconservative part leads to an increased damping signal in the oscillator electronics caused by an increase in the energy required to maintain a constant oscillation amplitude. The frequency shift in lateral force FM-AFM is described by equations similar to the case of the normal force FM-AFM, except that the different geometry has to be taken into account. Using the calculations from ref. 19 the frequency shift

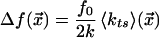is obtained with an average tip sample gradient

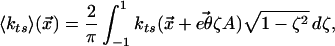where the unit vector e_θ = (0, cosθ, sinθ)^T points in the direction of the oscillation (see Fig. 1B). The force gradient k_ts is the second derivative of the tip-sample potential V_ts with respect to the coordinate along the oscillation axis of the force sensor, that is k_ts = ∂²V_ts/∂y′², where y′ is parallel to q′ as shown in Fig. 1B.

In addition to the frequency shift, the signal that controls the oscillation amplitude of the cantilever (gain signal g) is recorded. If the tip of the cantilever is far from the sample, the damping of the cantilever is due to internal dissipation and the energy loss per oscillation cycle is given by

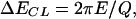where E = kA²/2 is the energy of the cantilever, and Q is its quality factor. If additional damping occurs due to a hysteresis in the tip-sample force F_ts, more energy has to be fed back into the cantilever for each oscillation cycle to retain a constant amplitude.

The dissipated energy is given by

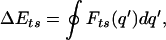where the integration extends over a full oscillation cycle. The energy dissipated during one oscillation cycle is accessible through an output terminal of the oscillator circuit (9). Thus, three physical parameters are recorded in the experiment: the average tunneling current, the frequency shift corresponding to an average lateral force gradient, and the dissipation energy per oscillation cycle.

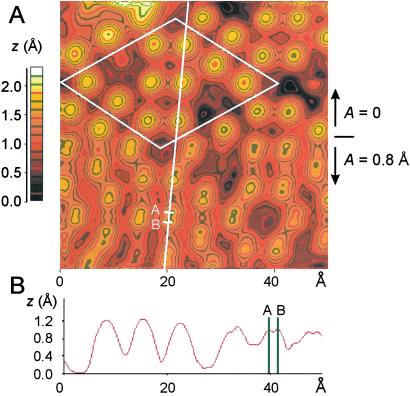
Fig. 2 is a topographic image of an Si(111)-(7 × 7) surface, where the oscillation amplitude of the lateral force sensor was zero for the top half of the image, and A = 0.8 Å at the bottom half. Consequently, in the bottom half each adatom appears to split into two adatoms, with a distance of 2A = 1.6 Å. Although the average force gradient and the dissipation per cycle were recorded parallel to the topography in Fig. 2, the forces were too weak to cause detectable variations in 〈k_ts〉 or ΔE_ts.

Fig 2.

(A) Topographic scanning tunneling microscopy image of the Si(111)-(7 × 7) surface recorded with a sample bias voltage of 1.6 V and an average tunneling current of 150 pA. The top half of the image was acquired with a nonoscillating sensor, and the lower half was recorded with an oscillation amplitude A = 0.8 Å. The tip was oscillating parallel to the surface. (B) Contour line, showing the split adatoms in the lower section of the image. The distance of the two subpeaks is twice the oscillation amplitude (1.6 Å). The white diamond indicates the surface unit cell with a short diagonal of 26.9 Å and a long diagonal of 46.6 Å.

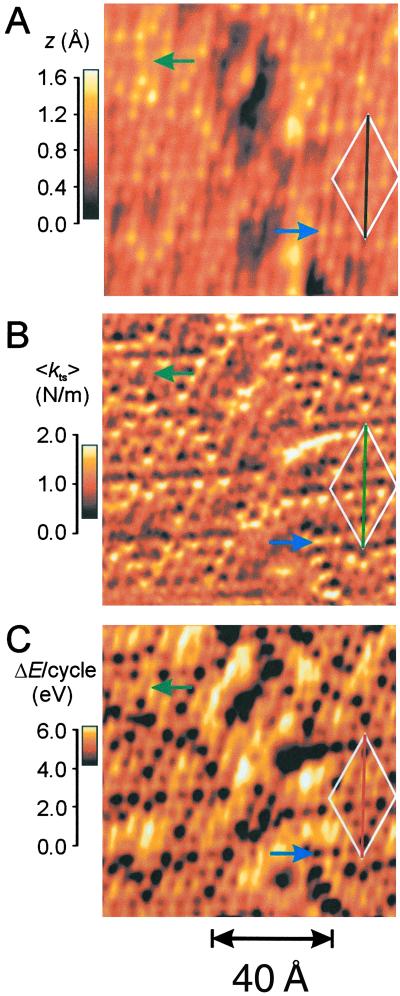
To analyze the dissipation, in an optimized experiment illustrated in Fig. 3, a much smaller tunneling impedance and thus a smaller tip-sample distance was used. Fig. 3 shows a simultaneous record of the three channels: A, topography z; B, average force gradient 〈k_ts〉; and C, energy loss per cycle. Like in Fig. 2, the feedback is set to topographic scanning tunneling microscopy mode, i.e., the average tunneling current (averaged over a time of at least 1/f₀ ≈ 100 μsec) is kept constant, and z is adjusted accordingly. The tip is tilted deliberately by θ ≈ 6°. This tilt angle is sufficient to enable atomic resolution imaging with an amplitude of A = 3 Å. Both the frequency shift and the damping vary strongly on the atomic scale, and single atomic defects are visible in frequency-shift and dissipation data.

Fig 3.

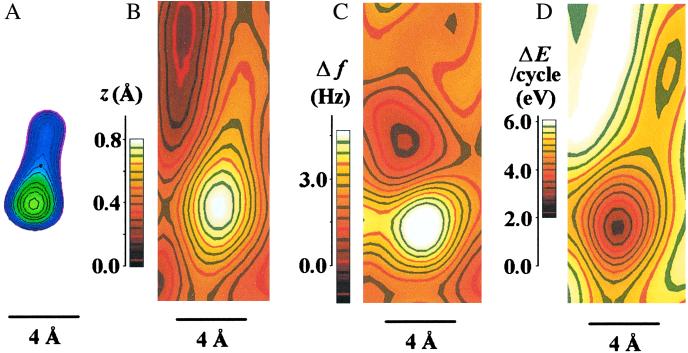
Topography (A), average lateral stiffness (B), and damping signal (C) recorded simultaneously while imaging an Si(111)-(7 × 7) surface. The green arrows indicate an atomic defect (missing corner adatom). Parameters: feedback on average tunneling current, 400 pA; sample bias voltage, −0.8 V; scanning speed, 4 lines per sec (vertical); cantilever oscillation amplitude, A = 3 Å; tilt angle, θ ≈ 6°; cantilever spring constant, k = 1,350 N/m; and eigenfrequency, f₀ = 10,214 Hz. The white diamonds indicate the surface unit cells. The black, green, and red lines across the long diagonals of the unit cells correspond to the traces where topography, frequency shift, and damping are plotted in Fig. 4. The blue arrows indicate the atom that is shown in magnification in Fig. 5 B–D.

The lateral forces acting between tip and sample change the restoring forces of the vibrating cantilever and cause a frequency shift. The largest frequency shifts in Fig. 3B occur directly above the adatoms and amount to +7.38 Hz. The frequency shift is positive, because the bond between tip atom t and sample atom s₁ (see Fig. 1B) increases the effective spring constant of the cantilever. According to Eq. 1 this frequency shift corresponds to an average lateral stiffness of the tip-sample contact of 1.95 N/m.

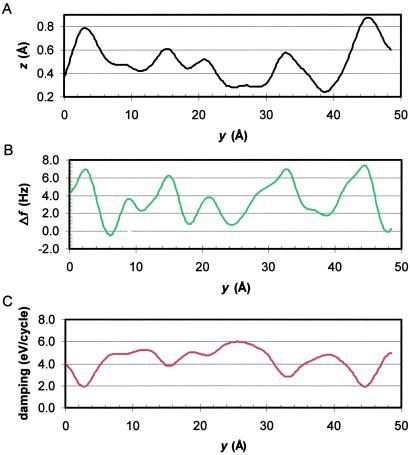
Because the lateral tip-sample forces are not conservative, more energy is required to drive the cantilever at a constant amplitude when the tip is close to the sample. With A = 3 Å, k = 1,350 N/m, and Q = 1,180, Eq. 3 yields an intrinsic energy loss of our cantilever of 2.0 eV per cycle. Fig. 3C shows the lateral variation of the dissipation energy. Directly above the adatoms the total energy loss is 2.1 eV per cycle—almost no extra damping is observed. However, between the adatoms the energy loss per cycle is three times higher. The brightest areas in Fig. 3C correspond to an energy loss of 6 eV per cycle, thus 4 eV per cycle are due to the tip-sample dissipation. Fig. 4 shows the traces of topography, frequency shift, and damping along the long diagonal of the Si(111)-(7 × 7) unit cell (indicated with black, green, and red tracks in Fig. 3 A–C). To interpret the data, it is important to consider the geometric positions between tip and sample atom. For the case shown in Fig. 2 where θ = 0°, it is trivial to find the zero position of the cantilever: it is exactly in the center of the double peaks in an adatom image. For θ ≠ 0° and larger amplitudes where the adatom images become blurred, a calculation helps to find the zero position of the cantilever with respect to the maximum in the topography image. This is done in Fig. 5A using the experimental parameters of θ = 6° and A = 3 Å. The maximum in the topographic image is shifted by −2.4 Å in the y (vertical) direction, which explains why we observe positive frequency shifts at the topographic maxima: the bond between tip and sample acts as an additional restoring force to the deflected cantilever and thereby increases its frequency. As evident from Figs. 4B and 5C, there are sections in the image with slight negative frequency shifts. Negative frequency shifts occur when the y distance between cantilever and closest adatom slightly exceeds A and no other sample atoms repulsively interact with the tip atom at the same time. Fig. 5D shows the dissipation map around the adatom. Interestingly, there is almost zero tip-sample dissipation when the cantilever is positioned directly over the adatom. The positive frequency shift at these points indicates a “bond” between tip and sample atom. Apparently, this bond does not break during the oscillation. However, when the cantilever is further away from the adatom, each time it enters the attractive potential a bond is created and destroyed again when the cantilever moves away. When the bond breaks, the bonding partners are deflected from their equilibrium position much further than by thermal agitation. When this deflection is released, the atom vibrates with phonon frequencies (teraHertz) and dissipates the stored energy via lattice vibrations into heat. Because typical phonon frequencies are 9 orders of magnitude larger than the oscillation frequency of the cantilever, by the time the tip approaches the sample atom again the vibrational amplitude of the sample atom has decreased to its thermal equilibrium value. This is the mechanism (“plucking action of one atom on the other”) described by Tomlinson on page 910 of his landmark paper (1). The maximal tip-sample dissipation per cycle is ≈4 eV (see Fig. 5D). This maximum occurs at a position where the front atom t vibrates between two sample atoms s₁ and s₂. Because phonons are created in approaching both s₁ and s₂, in a single atomic dissipation process an energy of 2 eV is released. This is in good agreement with a recent estimation (21) that found 1 eV per basic process.

Fig 4.

Plot of topography (A), frequency shift (B), and damping signal (C) recorded along the long diagonal of the unit cell of an Si(111)-(7 × 7) surface (see Fig. 3).

Fig 5.

(A) Simulation of a topographic image of a single adatom on silicon recorded with a laterally oscillating tip (amplitude, 3 Å; tilt angle, θ = 6°). Both the tip and sample states were assumed to have a p-type symmetry, yielding a tunneling matrix element proportional to cos⁴(ϕ)e^−2κr (20), where ϕ is the angle between the vector connecting tip and sample atom and the surface normal, r is the distance between tip and sample atom, and κ is the decay constant of the tunneling current (here, κ = 1 Å⁻¹ is used as a typical value after ref. 20). The image is a map of constant average tunneling current. The position of the adatom is depicted with a black dot. The distance of the adatom and the maximum height in the image is 2.4 Å, i.e., 20% less than the oscillation amplitude A. The vertical distance between the contour lines is equal to that shown in B (5 pm). Thermal excitation and quantum mechanical zero-point motion are not considered in this simulation; therefore the simulated image is sharper than the experimental image shown in B. (B) Experimental topographic image of a silicon adatom with θ ≈ 6° and A ≈ 3 Å (enlargement of the adatom marked with a blue arrow in Fig. 3A). The oscillation of the cantilever is not exactly parallel to the y (vertical) axis but is rotated by −10°. (C) Frequency-shift image of a single adatom on silicon recorded with a laterally oscillating tip (amplitude, 3 Å; tilt angle, θ ≈ 6°) showing exactly the same area as in B. The location where maximum positive frequency shift occurs does not coincide exactly with the maximum in the topography. (D) Corresponding damping data, again showing exactly the same section as B and C. Minimum damping occurs at the site where the frequency shift is maximal.

In summary, AFM with true atomic resolution using lateral forces has been established by showing that both conservative and dissipative force components exhibit clear variations on the atomic scale. Challenges remain in the further reduction of noise levels to facilitate operation with even smaller amplitudes and in research for finding alternate quasimonotonic interaction signals without harnessing a tunneling current. Potential applications of lateral force microscopy with true atomic resolution not only include the atomic study of friction and the measurement of the lateral stiffness of adatoms but also the measurement of the forces necessary for atomic manipulation (22).

Abbreviations

• AFM, atomic force microscopy

• FM, frequency modulation