Revisiting the kinetics of nitric oxide (NO) binding to soluble guanylate cyclase: The simple NO-binding model is incorrect

Abstract

Soluble guanylate cyclase (sGC) is a ferrous iron hemoprotein receptor for nitric oxide (NO). NO binding to the heme activates the enzyme 300-fold. sGC as isolated is five-coordinate, ferrous with histidine as the axial ligand. The NO-activated enzyme is a five-coordinate nitrosyl complex where the axial histidine bond is broken. Past studies using rapid-reaction kinetics demonstrated that both the formation of a six-coordinate intermediate and the conversion of the intermediate to the activated five-coordinate nitrosyl complex depended on the concentration of NO. A model invoking a second NO molecule as a catalyst for the conversion of the six-coordinate intermediate to the five-coordinate sGC–NO complex was proposed to explain the observed kinetic data. A recent study [Bellamy, T. C., Wood, J. & Garthwaite, J. (2002) Proc. Natl. Acad. Sci. USA 99, 507–510] concluded that a simple two-step binding model explains the results. Here we show through further analysis and simulations of previous data that the simple two-step binding model cannot be used to describe our results. Instead we show that a slightly more complex two-step binding model, where NO is used as a ligand in the first step and a catalyst in the second step, can describe our results quite satisfactorily. These new simulations combined with the previous activation data lead to the conclusion that the intermediate six-coordinate sGC–NO complex has substantial activity. The model derived from our simulations also can account for the slow deactivation of sGC that has been observed in vitro.

The physiological importance of nitric oxide (NO) signaling is now widely appreciated (1–3). NO, synthesized by NO synthase, typically acts in a paracrine fashion, where NO synthesized in one cell acts on a target in an adjacent cell. The best-characterized example of this paracrine action is endothelial–smooth muscle NO signaling that leads to relaxation of the muscle (vasodilation). The receptor for NO in smooth muscle as well as other target tissues is the soluble isoform of guanylate cyclase (sGC; ref. 3). A signaling role for NO has also been established definitively in both the central and peripheral nervous systems (2). sGC is a heterodimeric hemoprotein composed of α and β subunits and catalyzes the conversion of GTP to cGMP and pyrophosphate (3). sGC is activated by as much as 300-fold when NO binds to the heme cofactor. This activation results in a burst of the second messenger, cGMP, which then activates cGMP-dependent protein kinases and triggers various biological responses including smooth muscle relaxation.

The ferrous iron of the heme cofactor is ligated to the β subunit via a histidine residue (H105 in the rat β1 subunit; ref. 4–6) and has unique properties concordant with its function as a specific NO trap (7–11). For example, although the porphyrin is identical to that in hemoglobin and myoglobin in oxidation state and proximal histidyl ligation, sGC does not bind oxygen (7, 12, 13). This is crucial, given the concentration of O₂ (≈30 μM) relative to that of NO (≈1 nM) in the target cell. A weak Fe—His bond plays a significant role in the ability of the protein to bind NO selectively over O₂ (8, 9). Cytochrome c′ is a prokaryotic hemoprotein with ligand-binding properties (i.e., it binds NO and CO but not O₂) and spectral characteristics that are similar to sGC (14). The kinetics of NO binding along with the structures available for cytochrome c′ are proving to be useful models for sGC (15–17).

We recently described rapid kinetic studies of the binding of NO to sGC and the resultant activation of sGC (11). The rate constant for NO binding to the heme in sGC was shown to be >1.4 × 10⁸ M⁻¹⋅s⁻¹ at 4°C, which is greater than for any other known hemoprotein. It was suggested that this very rapid binding of NO permits sGC to compete effectively with other NO scavengers in cells. It was shown that the binding of NO to sGC (even at stoichiometric levels) proceeds in a two-phase reaction that initially results in rapid and essentially full formation of a six-coordinate (6C) ferrous nitrosyl heme complex. This complex has a spectral maximum at 420 nm (11, 18). Subsequently, the weakly bound proximal H105 dissociates from the 6C NO–heme complex to form a five-coordinate (5C) ferrous NO–heme complex (11, 18). Both the 5C ferrous NO–heme complex (5C sGC–NO) and the 6C ferrous NO–heme complex (6C sGC–NO) were definitively assigned by several groups by using a variety of spectroscopic techniques. It has been proposed that cleavage of the Fe—H105 bond triggers conformational changes in sGC that greatly increase the activity of the enzyme (≥300-fold). Our rapid quenching experiments demonstrated that the conversion of the 6C species to the 5C NO-bound ferrous species was required for full activation of sGC (11).

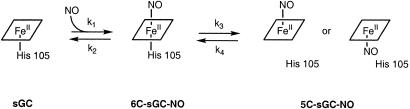
The activation of sGC by NO is complicated (19). As expected, the rate of formation of the 6C intermediate, with a spectral peak at 420 nm, was linearly dependent on NO concentration (19). Unexpectedly, the rate of dissociation of H105 from the heme to form the 5C NO complex was also linearly dependent on the concentration of NO over at least a 1,000-fold range (11). This dependence of NO implied that a second NO molecule is involved in the transformation that leads to activation of sGC. A model of the steps involved that is based solely on our previous results is presented here in Scheme . We proposed that the concentration of NO controls both how much enzyme is activated under any given set of conditions as well as how fast the enzyme is activated. The model shown in Scheme shows explicitly the key rate constants involved in NO activation of the enzyme that were discussed in Zhao et al. (11). We reported then the following values: k₁ > 1.4 × 10⁸ M⁻¹⋅s⁻¹, k₃ = 2.4 × 10⁵ M⁻¹⋅s⁻¹, and k₅ = 0.0087 s⁻¹, all at 4°C.

Scheme 1.

Model for activation of sGC. In the conversion of the 6C species to the 5C NO–heme complex (k₃), NO acts as a catalyst in the reaction such that it is not consumed. Simulations (vide infra) are consistent with this. The step represented by k₅ does not involve NO and shows NO bound on the distal and proximal sides of the heme.

Several recent publications (15, 20–22) have addressed specifically some aspects of the findings in our publication (11). One of these papers by Bellamy et al. (22) claimed that it was not necessary or warranted to invoke the interaction of NO in the second step to account for our observations. A model involving a simple two-step (STS) activation process with only the first step involving a concentration dependence on NO, was deemed sufficient to describe our previously published data (Scheme ).

Scheme 2.

STS model for sGC activation. This model is a subset of that shown in Scheme . It excludes k₅ and makes k₃ independent of NO.

Here we show that the STS binding model, in which there is a single NO-binding event (22), does not model the binding events correctly, and that the assumptions used by Bellamy et al. were incorrect. In addition, we have analyzed further the data from Zhao et al. (11) to provide in this report new insight into both activation and deactivation sGC.

Methods

Simulations.

Simulations of the two-step model described by Scheme used a numerical integration method based on a fourth-order Runge–Kutta algorithm (23), which are part of Program A, written by R. Chang, C. J. Chiu, J. Dinverno, and D.P.B. The model uses NO as a catalyst in the second step such that the rate depends on the NO concentration, but NO is not consumed in this step. The natural rate of conversion of the 6C to the 5C NO complex in the absence of free NO is accounted for by k₅. We used the following molar absorbencies at 431 nm: ɛ_sGC = 124 mM⁻¹⋅cm⁻¹, ɛ_6C = 66 mM⁻¹⋅cm⁻¹, and ɛ_5C = 46 mM⁻¹⋅cm⁻¹ (6C = 6C sGC–NO and 5C = 5C sGC–NO).

Results and Discussion

Summary of Zhao et al. (11).

Fig. 1 A and B originally appeared as figure 2 b and c in Zhao et al. (11). Fig. 1A shows spectra generated during the course of the reaction of sGC (0.6 μM) with NO (0.57 μM). These data demonstrate that sGC is converted rapidly from the 5C ferrous resting form to the 6C NO–sGC complex. Importantly, the conversion of ferrous sGC to the 6C NO complex, which is finished within 100 ms at 4°C, leads essentially to a complete formation of the 6C complex even in the presence of low but stoichiometric quantities of NO. This result implies that the K_d for dissociation of the 6C complex toward resting ferrous sGC and NO is ≪1 μM, and that there is no measurable equilibrium between the 6C NO complex and the resting ferrous sGC and NO at the concentrations used. The 6C sGC–NO complex then converts to the 5C sGC–NO complex in a process exhibiting an isosbestic point at 407 nm. Fig. 1B shows that at a low NO concentration (0.59 μM) the second phase is very slow (t_1/2 ≈ 500 s), whereas with 500 μM NO this phase is characterized by a t_1/2 < 3 ms. At 500 μM NO, all of the first phase is complete within the dead time of the instrument, and nearly half of the second phase occurs within this period as well. Note that increasing the concentration of NO from 0.59 to 6.6 μM does not change the level of the absorbance at 431 nm after the first phase. This is because the first phase observed at 431 nm is caused mainly by the conversion of ferrous sGC to the 6C species, whereas the second is caused mainly by the conversion of the 6C intermediate to the 5C NO complex (see Fig. 1A). After the first phase there is no appreciable 5C resting form of sGC remaining such that the absorbance changes in the second phase are caused almost entirely by the conversion of the 6C sGC–NO complex to 5C sGC–NO.

Fig 1.

Data and simulations for the reaction of sGC with NO. (A) Spectra are shown of the ferrous sGC recorded before the reaction with NO (λ_Soret at 431 nm) of the 6C sGC–NO complex immediately after mixing sGC with NO (λ_Soret at 420 nm) and of 5C sGC–NO recorded 5 min after initiating the reaction (λ_Soret at 399 nm). A spectrum of a mixture of 6C and 5C NO complexes during conversion to the 5C NO complex helps to define the isosbestic point at 407 nm. The sGC concentration was 0.6 μM, and the NO concentration was 0.57 μM. Spectra were recorded at 200 nm/s. (B) The effect of NO concentration on the overall reaction was examined as follows: sGC (0.47 μM) was mixed anaerobically with 0.59, 1.53, 6.6, and 500 μM NO at 4°C, and absorbance changes at 431 nm are shown. (C) Simulations of the reactions in B according to Scheme . The values used are ɛ_sGC = 124 mM⁻¹⋅cm⁻¹, ɛ_6C = 66 mM⁻¹⋅cm⁻¹, and ɛ_5C = 46 mM⁻¹⋅cm⁻¹; k₁ = 1.55 × 10⁸ M⁻¹⋅s⁻¹, k₂ = 1 × 10⁻² s⁻¹, k₃ = 3.3 × 10⁵ M⁻¹⋅s⁻¹, k₄ = 1 × 10⁻³ s⁻¹, and k₅ = 5 × 10⁻⁴ s⁻¹. NO concentrations are indicated as solid circles (0.47 μM), open circles (1.53 μM), open squares (6.6 μM), and a solid line (500 μM). At the low concentration, the best fit was obtained with 0.47 μM NO. The instability of NO and the experimental design contributed to this loss, which is most pronounced at this low concentration. (D) Simulations of the STS model with the same extinction coefficients as in C and with the rate constants used by Bellamy et al. (22): k₁ = 8 × 10⁷ M⁻¹⋅s⁻¹, k₂ = 200 s⁻¹, k₃ = 1.3 s⁻¹, and k₄ = 6.6 × 10⁻² s⁻¹. Symbols are the same as in C. Note that in D the starting absorbance of the second phase varies with NO concentration, whereas in B (experimental data) and C (simulation based on our model) the second phase has the same starting absorbance when NO concentrations are in the 0.57–6.6 μM range. This indicates that the equilibrium between the 6C sGC–NO complex and ferrous sGC required by the Bellamy model lies almost fully toward 6C sGC–NO. [A and B are reproduced with permission from Zhao et al. (11) (Copyright 1999, Natl. Acad. Sci.).]

Simulations of NO Binding to sGC.

Fig. 1C shows the results of simulations for the concentrations of sGC and NO used in the experiments shown in Fig. 1B. The vertical line in Fig. 1C delineates the dead time of the stopped-flow instrument (≈3 ms) to show what fraction of the reaction was missed in the experiment in Fig. 1B. A rapid and full formation of the 6C sGC–NO intermediate is shown by the absorbance at the end of the first phase being the same for all concentrations, and it is clear that both phases strongly depend on NO concentration. The simulations closely mimic the experimental observations. The only discrepancy is that at the end of the first phase, the absorbance is slightly lower than anticipated from the spectral properties shown in Fig. 1A. If the experiments in Fig. 1B were actually recorded at a slightly shorter wavelength than 431 nm, the extinction coefficients would give results more closely resembling the recorded data. Simulations of the STS model using the rate constants from ref. 22 (k₁ = 8 × 10⁷ M⁻¹⋅s⁻¹, k₂ = 200 s⁻¹, k₃ = 1.3 s⁻¹, and k₄ = 0.066 s⁻¹) and the same extinction coefficients as in Fig. 1C are shown in Fig. 1D. (In the Bellamy et al. paper the simulations were presented as the fraction of the sGC in the free state rather than as absorbance data.) These simulations do not at all resemble the data in Fig. 1B. With appropriately chosen rate constants, the STS model predicts biphasic behavior for NO binding to sGC, including some dependence of the rate of the second step on NO concentration; however, the rapid equilibrium of the first phase is not stoichiometric, and the dependence of the second phase on NO concentration is much less pronounced. A model such as that in Scheme is required to fit this data.

The STS model (Scheme ), which is related closely to the Castillo–Katz model for receptor activation (24), is a subset of that in Scheme ; it excludes k₅ and makes k₃ independent of NO. The crucial premises for applying the STS model to this system are that resting sGC and its 6C NO complex be in rapid equilibrium with a substantial fraction of sGC in the free form, and that subsequent steps resulting in the dissociation of H105 to form the 5C NO–heme complex of sGC be considerably slower. Under conditions in which the ligand (NO) concentration is <k₂/k₁, the overall rate of the second step in this model will be observed to depend on NO concentration, because as the NO concentration is increased, the ratio (6C sGC–NO/sGC) will increase. This type of behavior is common for binding of substrates to many enzymes (see for example ref. 25, which shows an equivalent situation for the binding of NADP to cyclohexanone monooxygenase). However, as shown above, the STS model of Bellamy et al. (22) does not meet the critical criteria and clearly does not fit our data.

The primary errors in the analysis by Bellamy et al. were: (i) the absorbance changes at 431 nm were treated as if they were solely caused by the unbound ferrous sGC (in fact, each of the species has significant contributions to the absorbance, although only ferrous sGC has an absorbance maximum at 431 nm), and (ii) it was not recognized that the 6C sGC–NO complex was fully formed by the end of the first phase even when NO was present in stoichiometric concentrations compared with the enzyme. Thus, the second phase of the 431-nm trace was not caused by a decrease of unbound ferrous sGC but actually represents the conversion of the 6C NO–sGC complex to the 5C NO–sGC complex.

When analyzing receptor–ligand-binding kinetics, it is not always possible to monitor intermediates directly. Often only the free receptor and the composite of all the bound species can be distinguished, which can lead to some ambiguity in analyzing kinetics. By contrast, the data presented by Zhao et al. (11) enabled the identification and quantification of free sGC, the 6C sGC–NO intermediate, as well as the final active form (5C sGC–NO). This direct identification makes the analysis less ambiguous.

Activity of 6C sGC–NO.

Rapid quenching experiments involving mixing NO with sGC followed by analysis of cGMP formation showed that there was a lag before the onset of full activity of sGC occurred (11). The lag was approximately inversely proportional to the concentration of NO, up to 10 μM (Fig. 2A). At concentrations of NO > 10 μM, full activation occurred within the same time frame as a single turnover, such that the lag could not be discerned. From inspection of the data it was concluded that the activity of the 6C species was approximately at the basal level, whereas the 5C NO-bound species was ≈300-fold activated. Condorelli and George recently reported simulations of the entire activation-deactivation process in an attempt to explain NO activation in vivo (20). They modified our model to include dissociation of NO from the fully active 5C species, and they add a thiol-dependent dissociation step that would consume NO in the process. This latter step and simulations derived were used to provide an explanation for the in vivo deactivation, which is faster than that observed in vitro. Their simulations indicated that 6C sGC–NO could be as much as 50% as active as 5C sCG. With the simulations of Fig. 1C and the rapid-quenching results, it is possible to evaluate more directly the activity of the 6C sGC–NO complex under the conditions used by us in our earlier article (11). Fig. 2 B and C shows simulations of the concentrations of species calculated according to the model in Scheme for 10 and 0.75 μM NO (using 0.5 μM sGC), respectively. Although it is difficult to be quantitative because of the imprecision of the quenching data, it is clear that considerable activity is achieved before the 5C sGC–NO complex has formed fully. It can be estimated that the activity between 1 and 1.4 s using 0.75 μM NO is ≈50% of that when using 10 μM NO. However, at ≈0.4 s the activity is only 15–20% that when using 10 μM NO. Yet at either of these times using 0.75 μM NO only a small fraction of the enzyme has been converted to the 5C NO complex. This result suggests that initially, 6C sGC–NO is only partially active (near basal level), but even before the complete formation of 5C sGC–NO complex, substantial activity is realized.

Fig 2.

Time course after mixing NO with sGC of various species and of production of cGMP. (A) sGC [1 μM in 50 mM Hepes (pH 7.4) and 50 mM NaCl, 15 μl] was mixed rapidly with 15 μl of buffer containing GTP (3 mM), Mg²⁺ (10 mM), and NO in a Kintek rapid quench-flow device at 4°C and were quenched at appropriate times with 40 mM HCl. Data for NO concentrations after mixing at 0.75 μM (closed circles) or at 10 μM (open circles) are shown. The sGC heme concentration was 0.5 μM after mixing. Each point is the mean of the cGMP values determined for three measurements. (B) Simulation of the reaction of 0.5 μM sGC with 10 μM NO. (C) simulation of the reaction of 0.5 μM sGC with 0.75 μM NO. In B and C: sGC, closed circles; 6C sGC–NO, open circles; and 5C sGC–NO, open squares. [A is reproduced with permission from Zhao et al. (11) (Copyright 1999, Natl. Acad. Sci.).]

Comparison to Cytochrome c′.

Recently, an important study has shown that cytochrome c′ from Alcaligenes xylosoxidans (AXCP) also binds NO to form a 6C complex that converts to a 5C nitrosyl end product (17). AXCP, similar to sGC, binds both NO and CO but does not readily bind molecular oxygen. Moreover, analogous to sGC, both the rate of formation of the 6C NO-bound intermediate and the subsequent conversion to the 5C NO-bound product depend on the concentration of NO. Lawson et al. (15) showed by crystallographic studies that NO in the 5C complex of AXCP is bound on the proximal side of the heme, whereas CO is bound on the distal face. Using this information, Andrew et al. gave evidence that the first NO binds to the distal face of the heme, trans to the proximal H120 (16). They proposed that as H120 dissociates, a second molecule of NO binds to the heme. Because of the repulsive trans effect of the bound NO (partial transfer of the unpaired NO electron to the iron d orbital), 5C NO–heme complexes rather than 6C complexes are found more commonly (26, 27). This trans effect causes the less tightly bound NO to be displaced. In the case of AXCP, the more stereochemically hindered distal NO dissociates, leaving the proximal NO bound in the 5C complex, which explains how NO kinetically affects both phases but that only one NO is consumed in the overall binding. An analogous reaction sequence was suggested for sGC. Thus, a 6C NO complex initially forms to lead to a more weakened proximal H105 bond because of the trans effect, which could enable a second NO molecule to bind to the proximal face of the heme after H105 dissociates to give a transient 6C heme (with two NO molecules bound). The displaced H105 would thereby enable at least partial activation of sGC even before a 5C complex was realized fully. Subsequently, the trans effect would lead to displacement of one of the two NO molecules to yield the most stable 5C NO complex (Scheme ). Such a scenario could explain the observations discussed above, where significant activity appears before the 5C sGC–NO species is formed fully. Possibly, the spectral characteristics of the heme are not fully indicative of the conformation of the active site of sGC but only tell us that the heme is 6C.

In addition to the above mechanisms, there are other possibilities for a second molecule of NO acting in this transformation. These possibilities include (i) a second NO-binding site (nonheme) that interacts with the heme-nitrosyl to assist in loss of the proximal coordination, perhaps by increasing the trans effect of the bound NO, and (ii) nucleophilic addition of NO to the bound NO to generate a transient N—NO bond. Precedents exist for both of these possibilities (28–30).

Deactivation of 5C NO–sGC.

The deactivation of sGC is a critical point of control in the NO signal transduction pathway. Previous studies that formed the 5C sGC–NO complex followed by removal of free NO showed that the return of sGC to basal level activity by loss of NO occurs quite slowly, requiring several minutes (k_off ≈ 10⁻³ s⁻¹; refs. 31 and 32), whereas the deactivation in cells is substantially faster (33). The model of Scheme correctly predicts this behavior as shown in Fig. 3 for 5C sGC–NO at 4°C (from the simulations, the measured k_off ≈ 10⁻³ s⁻¹). Condorelli and George have shown by simulations that at concentrations of NO > 100 nM sGC will usually be activated almost fully (20). Because deactivation is slow and NO concentrations often can be ≥100 nM, it is very likely that there are other cellular mechanisms that contribute to the deactivation in vivo such that the transient response can be discontinued.

Fig 3.

Simulation of the return to free sGC after the removal of free NO from solution. 5C sGC–NO (0.47 μM) was used as the starting condition. The reaction was simulated according to Scheme and the rate constants in Fig. 1C, assuming that all free NO was removed from solution.

Summary

•   i.  The binding of NO to sGC to form the activated 5C sGC–NO complex occurs in two steps that are both dependent on the concentration of NO. Scheme shows the simplest model that can fit the observed data.

• ii.  The STS binding model in Scheme , in which there is a single NO-binding event as described by Bellamy et al. (22), does not model the binding events correctly. The conditions for applying that model were not appropriate.

• iii.  By using the model in Scheme , comparisons of simulations of concentrations to the activation data of Zhao et al. (11) predict that at least some forms of the 6C sGC–NO complex have substantial activity. It would seem that the 6C species formed initially has less activity than those formed later. This analysis refines the original conclusions of Zhao et al. and agrees (at least qualitatively) with those of Condorelli and George (20).

• iv.  The results of studies on cytochrome c′ by Andrew et al. (17) suggest a mechanism that can account for why the second step in activation of sGC depends on the concentration of NO. This mechanism involves the formation of a second intermediate, a transient, 6C di-NO complex. This complex may have substantial activity, because the proximal histidine will have dissociated already to allow protein conformational changes that are required for activation of the sGC for catalysis.

• v.  The two-step binding model of Scheme can account also for the slow deactivation of sGC. The dissociation of NO has been shown to be very slow in the absence of other cellular components. Thus, in the cell there are undoubtedly one or more other mechanisms for terminating the activity of sGC such that no more cGMP second messenger is produced.

Abbreviations

• sGC, soluble isoform of guanylate cyclase

• 6C, six-coordinate

• 5C, five-coordinate

• STS, simple two-step

• AXCP, cytochrome c′ from A. xylosoxidans