The mechanism of type IA topoisomerases

Abstract

The topology of cellular DNA is carefully controlled by enzymes called topoisomerases. By using single-molecule techniques, we monitored the activity of two type IA topoisomerases in real time under conditions in which single relaxation events were detected. The strict one-at-a-time removal of supercoils we observed establishes that these enzymes use an enzyme-bridged strand-passage mechanism that is well suited to their physiological roles and demonstrates a mechanistic unity with type II topoisomerases.

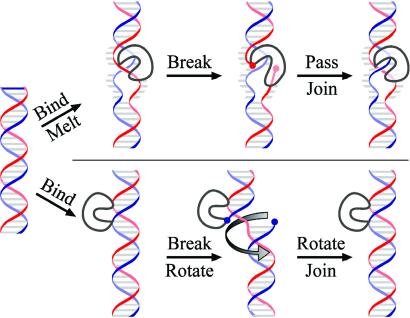
Topoisomerases are divided into two classes, depending on whether one strand (type I) or both strands (type II) of DNA are transiently broken to permit a change in topology (reviewed in refs. 1 and 2). Type I enzymes, the subject of this report, are found in all three kingdoms of the living world: bacteria, archaea, and eukarya (2). These enzymes are divided further into IA and IB subclasses that share no structural similarity and differ in reaction chemistry. Type I and II topoisomerases yield products that differ in DNA linking number (Lk) by 1 and 2, respectively (3–5). This result is often misinterpreted to indicate that the ΔLk for each round of catalysis must be 1 for type I enzymes and 2 for type II enzymes. However, this assumption is true only if the ΔLk per round is constant, as the experiments show only that the change per round is 1n and 2n, where n is an integer. This distinction is important because biochemical (6), kinetic (7), and structural (8) data imply that n is not equal to 1 for type IB enzymes but, for example, about 5 for the vaccinia topoisomerase. Such a nonunitary ΔLk is explained most simply by a strand-rotation model (Fig. 1 Lower) for type IB action in which the enzyme breaks one strand of the DNA helix by addition across a phosphodiester bond, allowing limited rotation about the intact strand to relax several supercoils before resealing occurs (8). A strand-rotation mechanism differs fundamentally from a sign inversion or an enzyme-bridged strand-passage mechanism (Fig. 1 Upper) in which ΔLk must be uniquely 1 for type I enzymes (3, 9). In the latter model, both ends of the transient DNA nick are bound to the topoisomerase, preventing DNA swiveling but allowing passage of a second DNA strand through the enzyme-bridged gate before resealing.

Fig 1.

Proposed mechanisms for type I topoisomerases. Shown is a segment of DNA in a (−) supercoiled molecule that is acted on by a type I topoisomerase (gray). (Upper) An enzyme-bridged mechanism for type IA topoisomerases. The free energy of (−) supercoiling promotes the melting of the DNA upon enzyme binding and the stabilization of a (−) crossing of single strands of DNA. After cleavage of one strand of DNA, the enzyme bridges the break by covalent attachment to one end and noncovalent binding to the other. Passage of the intact strand through the break inverts the sign of the crossing. The result is a ΔLk of 1 per round of catalysis. (Lower) A strand-rotation mechanism, as proposed for type IB topoisomerases. After binding to duplex DNA, the enzyme nicks one strand by addition across the phosphodiester bond and thereby becomes covalently attached to one end of the nick. The other end of the nick is not bound, resulting in rotation of the free end about the intact strand before rejoining of the DNA ends. The result is the relaxation of several supercoils and a nonunity ΔLk per round of catalysis.

An enzyme-bridging mechanism for type II enzymes has been verified by single-molecule experiments showing that in the elementary catalytic cycle, ΔLk is uniquely 2 (10, 11). No such experiments have been done with type I enzymes. Although biochemical (9, 12, 13) and structural (14) data suggest a strand-passage mechanism for the type IA subclass, the mechanism has not been established convincingly for either subclass of type I enzymes. It is important to know whether a strand rotation or an enzyme-bridged mechanism operates for type I topoisomerases, not only for the intrinsic enzymological interest but also because the mechanism is critical to understanding the complex roles of these enzymes in cells. Thus, the strand-rotation model has the advantage of allowing a rapid and efficient relaxation of supercoils, for example, ahead of the replication fork (7). The enzyme-bridged strand-passage mechanism leads to much more controlled topological changes. Because type IA enzymes bind preferentially to single-stranded DNA (1), they are limited to relaxation of (−) supercoils above a threshold value where denaturation of duplex DNA by enzyme binding is thermodynamically favored and to the disentanglement of single-stranded regions of DNA. Indeed, the relaxation of (−) supercoils is the essential role of topoisomerase I (topo I) in bacteria (1). Disentanglement is likely the critical function of topo III, which can act in complex with a helicase whose malfunction is implicated in several human diseases (15–19).

In the present work, we followed the action of a mesophilic and a thermophilic bacterial type IA topoisomerase on single molecules of DNA in real time. We show that these enzymes do indeed act by a strand-passage mechanism, as we observed a |ΔLk| = 1 in individual steps of DNA relaxation. We also have determined the kinetic parameters of both enzymes and found that stretching DNA dramatically reduces their activity.

Materials and Methods

Magnetic Tweezers.

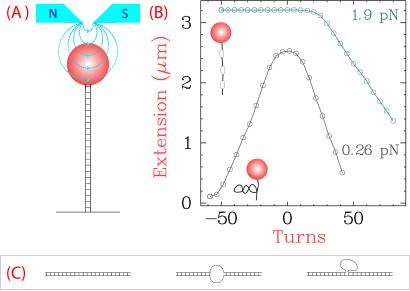
Single DNA molecules, attached at one end to a glass capillary and at the other to a magnetic bead, were maintained under tension by the field gradient of two small permanent magnets placed above the sample (Fig. 2A). The NdFeB magnets (6 mm × 6 mm × 5 mm) were separated by 1.4 mm. Images of the bead grabbed by a charge-coupled device camera (model CV-M30, JAI, Copenhagen, Denmark) determine its distance l from the surface and the magnitude of its transverse fluctuations 〈δx²〉. From these measurements, we calculate the force exerted on the DNA molecule F = k_BTl/〈δx²〉, where k_B is the Boltzmann constant and T is the temperature (20). Translation of the magnets controls the magnitude of this force (F < 50 pN), whereas rotation of the magnets controls the supercoiling density σ, defined as ΔLk divided by the Lk of relaxed DNA.

Fig 2.

The experimental configuration. (A) DNA molecules were tagged at their ends with biotin and digoxygenin, allowing attachment to a streptavidin-coated magnetic bead and an antidigoxygenin-coated glass surface. Translation and rotation of a pair of magnets above the DNA molecule changed the extension of the DNA, which was recorded by tracking of the bead's position with an inverted microscope. (B) The behavior of an 11.5-kb duplex DNA molecule under superhelical stress at two applied forces. At F = 0.26 pN, (+) and (−) superhelical turns equivalently reduced DNA extension through the formation of plectonemic supercoils. Increase of the force to 1.9 pN resulted in an asymmetry of the supercoiling vs. extension curve because denatured regions form at the expense of plectonemes in (−) but not (+) supercoiled DNA. For this DNA, 50 turns caused a |σ| of 0.045. (C) Three different DNAs were used in this study: fully duplex 11.5-kb DNA, 8.7-kb duplex DNA with a symmetric mismatch of 12 nucleotides, and 8.7-kb DNA with an asymmetric bulge of 25 unpaired nucleotides.

DNA Constructs.

We used three DNA substrates (Fig. 2C). To observe topo I action on (−) supercoiled DNA, we used an 11.5-kb double-stranded DNA multiply labeled with biotin or digoxygenin at its extremities. The DNA molecules were incubated at room temperature for 5 min with 1.0-μm diameter streptavidin-coated paramagnetic beads (Merck). The DNA concentration was low enough that no more than one DNA molecule was bound, on average, to each magnetic bead. The digoxygenin end of the DNA was bound to a glass capillary surface coated with anti-digoxygenin. The capillary surface was also coated with polyglutamic acid (3 mg/ml) to minimize nonspecific interactions.

To observe topoisomerase I (topo I) action on (+) supercoiled DNA, we used an 8.7-kb duplex DNA that contained a small single-stranded region (13) consisting either of a mismatch of 12 unpaired nucleotides or a bulge of 25 nucleotides midway through the DNA. To form the mismatched construct, two 60-nt synthetic polynucleotides were annealed. The synthetic sequences were complementary, except for 12 nucleotides at their center, where cytidylic residues were opposite those of thymidylic residues. The annealed 60-mers were ligated onto one end of the 8.7-kb plasmid, which was then cyclized. The resulting plasmid was digested with restriction endonucleases that cut 4.2 kb upstream and 4.7 kb downstream from the insert to generate a linear molecule with the insert near the center. The ends of the DNA were tagged with digoxygenin- and biotin-labeled DNA fragments (≈400 bp long). An analogous protocol yielded the DNA with a bulge. These constructs were attached to a capillary surface and a magnetic bead by using the procedure described above.

Enzymes.

Escherichia coli topo I was purified from an overproducing strain obtained from R. DiGate (University of Maryland School of Pharmacy, Baltimore) that contains a topB disruption to ensure there is no contaminating topo III (21). Purification was as described (22) with the following modifications: (i) the lysate was applied to a DE-52 cellulose column in buffer containing 50 mM KCl, and (ii) the unbound protein was collected and chromatographed on a single-stranded DNA cellulose column by using a 0.25–2 M KCl gradient. To prepare the Thermotoga maritima topo I, the gene was amplified by using the PCR from genomic DNA and subcloned into the pET29b expression vector. The recombinant protein was expressed in E. coli and purified as described (23).

Topo I reactions contained 50 mM Tris⋅HCl, pH 8.0, 120 mM NaCl, 10 mM KCl, 3 mM MgCl₂, 1 mM DTT, 200 μg/ml BSA, and 0.1% Tween 20. The MgCl₂ concentration was reduced to 0.25 mM to observe step-wise activity of topo I.

Numerical Analysis.

To cancel slow drifts of the optical microscope, we measured the distance l(t) between the tethered bead and a reference bead stuck to the surface. For the analysis of topoisomerase steps, these raw data l(t) were filtered at 2 Hz. Steps of size S occurring at times t_S were fit by using a sliding Heaviside (step) function (24): l_step(t) = Sθ(t − t_S) + l₀ defined over a time window of typical size t_av. That is, for every time point t₀ of the data set, the parameters of the step function (S, t_S, l₀) were fit to minimize the error χ² = [l(t) − l_step(t)]² in the time window t₀ < t < t₀ + t_av, where only one step was expected. The parameters that consistently scored for minima of χ² were selected as steps. These were then binned to form histograms.

Results and Discussion

Our experiments are conducted on single DNA molecules maintained under tension by the field gradient of small magnets placed above a paramagnetic bead attached to the DNA (Fig. 2A). Translation of these magnets varies the magnitude of the applied force (20), whereas their rotation controls the degree of supercoiling, σ, applied to the DNA. Specification of these two parameters permits precise control of the topology of the DNA molecule (Fig. 2B). At a low force (0.26 pN), (+) and (−) σ equivalently reduced DNA extension by formation of plectonemic supercoils. At a higher force (1.9 pN), (−) σ caused DNA untwisting in place of supercoiling. Plectonemic supercoiling still resulted at this force from a (+) σ. We used three DNA substrates (Fig. 2C). Besides an 11.5-kb double-stranded DNA, we used an 8.7-kb duplex DNA that contained a small single-stranded region, consisting either of a mismatch of 12 unpaired nucleotides or a bulge of 25 nucleotides midway through the DNA. Duplex DNA with a single-stranded region is a particularly good substrate for type IA enzymes (13). We used two type IA topoisomerases, from E. coli and T. maritima, that differ greatly in amino acid sequence (23). The enzyme from the hyperthermophilic T. maritima has a temperature optimum of 80° C but retains high activity at room temperature. In this report, we focus on the more extensively characterized topo I from E. coli.

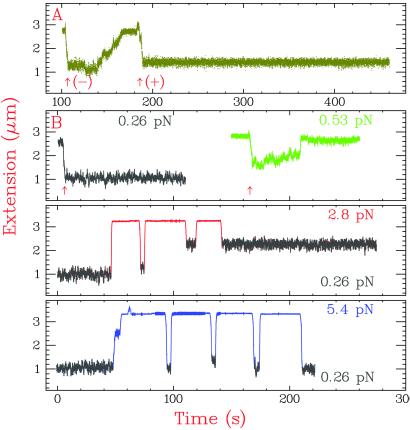
We began by showing with our apparatus that E. coli topo I removes (−), but not (+), supercoils from DNA, its signature activity. Supercoils were incorporated into a 11.5-kb duplex DNA by rotation of the magnets, with resultant shortening of the molecule's extension (Fig. 2B). With 380 pM E. coli topo I acting on a DNA under 0.69 pN of tension, we observed brisk relaxation of (−) supercoils but no activity with (+) supercoils (Fig. 3A).

Fig 3.

Relaxation of (−) supercoiled DNA by E. coli topo I. The substrate was fully duplex 11.5-kb DNA. Arrows (↑) indicate the introduction of supercoiling by rotation of the magnets. (A) Topo I relaxes (−) supercoils, as shown by the increase in DNA extension, but cannot relax (+) supercoils. (B) The effect of force on (−) supercoil relaxation. DNA supercoiling density equaled −0.03. The topo I concentration was 380 pM, which was above the K_d of ≈200 pM that we estimated with single-stranded DNA. Topo I is inactive at F = 0.26 pN (gray) but active at F = 0.53 pN (green), where more of the (−) superhelical stress is partitioned into DNA untwisting. To determine topo I activity at F > 1 pN, where DNA extension is independent of (−) superhelical density (Fig. 2B), we periodically monitored DNA extension at F = 0.26 pN. For example, to measure topo I activity at 2.8 pN (red), we measured the degree of (−) supercoiling of the DNA at 0.26 pN, increased the force to 2.8 pN on a time scale that was fast compared with that of topo I activity, added topo I, and reduced the force to 0.26 pN to remeasure the degree of supercoiling. Thus, we found that topo I remained active at 2.8 pN, but at a reduced rate. At F = 5.4 pN (blue), no topo I activity was detected.

Next, we studied the effect of force on topo I relaxation of (−) supercoiled DNA (Fig. 3B). There was a force optimum for topo I activity. At a low force, 0.26 pN, no topo I activity was observed on DNA with σ = −0.03. When the force was increased to 0.53 pN, topo I relaxed (−) supercoils efficiently at an average rate of ≈1 supercoil per s. The increased force caused more of the stress of the (−) ΔLk to be converted to untwisting rather than writhe, which promotes enzyme binding (25). Interestingly, the rate of relaxation was lower at 2.8 pN and was undetectable at higher forces. This result was unexpected because denaturation bubbles become more prominent at higher forces. Thus, beyond a minimal force required for the creation of a denaturation bubble, the rate of topo I activity diminished with increasing force, suggesting that the enzyme has to move DNA against the force during DNA binding or strand transport. The decrease in activity as a function of force suggested to us that single relaxation events might be observable at a large enough force.

To quantify the elementary catalytic steps of a single molecule of topo I on supercoiled DNA, we needed [1] a single enzyme acting on DNA in reaction conditions within the physiological range, [2] a rate of supercoil removal slower than 1 per s, our time-resolution limit, and [3] an increase in DNA extension per supercoil removal readily observable above the noise. The properties of topo I relaxation of (−) supercoiled DNA presented technical obstacles to fulfilling these criteria.

Therefore, we adopted a strategy based on the observation of Kirkegaard and Wang (13) that a (+) supercoiled DNA with an engineered short denatured region is an excellent substrate for topo I. Thus, we made a DNA construct with a central 12-bp mismatch (Fig. 2C). We expected topo I would bind well to this region of single-stranded DNA, and that the short length of the mismatch would allow only one topo I to bind each DNA molecule, fulfilling criterion 1.

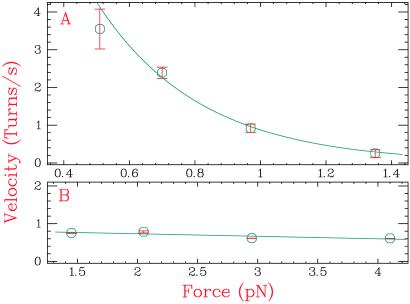
As expected, topo I relaxed (+) supercoiling of this substrate. The rate of (+) supercoil removal, independent of supercoiling density, decreased with applied force (Fig. 4A), just as we had observed with (−) supercoiled DNA. This control of the relaxation rate of topo I by force helped us fulfill criterion 2. The dependence could be fit to an Arrhenius law for the relaxation rate v: v ∼ exp(−Fδ/k_BT), yielding an effective length δ of ≈10 nm associated with the work performed against the force F by an enzyme of only ≈5 nm. This very large deformation of the DNA substrate is surprising. Perhaps it is associated with insertion of the enzyme between the two DNA strands upon binding. A parallel diminution of rate with applied force was observed with the T. maritima enzyme (data not shown). In contrast, with a DNA construct with a bulge of 25 nt instead of the mismatch, the relaxation rate was insensitive to applied force (Fig. 4B). We interpret this difference as due to whether the single-stranded region to which the enzyme binds is under tension. With the mismatch, the work performed by the enzyme against the tension increases with applied force, thus slowing it down.

Fig 4.

Rate of (+) supercoil removal by topo I as a function of the applied force. (A) Variation of the enzymatic rate with force on a DNA construct containing a symmetric mismatch of 12 nucleotides. The data shown are for E. coli topo I (similar results were obtained with T. maritima topo I) and were fit by using v ∼ exp(−Fδ/k_BT), yielding δ (the distance DNA moves during the force-sensitive step) of about 10 nm. (B) Variation of the enzymatic rate with force on a DNA construct containing an asymmetric bulge of 25 nucleotides. The data shown are for T. maritima topo I, but similar results were obtained with the E. coli enzyme. The results were fit to a straight line that deviates from a flat line by less than 10%.

Slowing down enzymatic activity at high forces on a DNA with plectonemic supercoils presented two major advantages in terms of signal-to-noise. First, it permitted direct monitoring of topo I activity through the increase in DNA extension, an option compromised by DNA denaturation in (−) supercoiled DNA (Fig. 3B). Relaxation of one (+) supercoil (ΔLk = −1) resulted in a 35.0-nm increase in length at F = 2.0 pN (Fig. 2B). Second, it enabled these measurements to be made with lower noise, because the amplitude of the bead's fluctuations decreased with the applied force. The combination of these factors helped satisfy criterion 3. The final adjustment we made was to slow the reaction rate by decreasing the magnesium concentration to 0.25 mM. This completed the satisfaction of criterion 2.

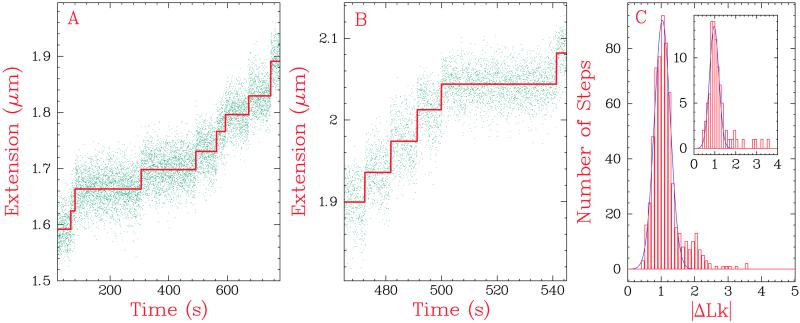
We could now test whether type IA topoisomerases used an enzyme-bridged strand-passage mechanism or a strand-rotation mechanism. We found that the (+) supercoiled construct with a 12-bp mismatch was relaxed by E. coli and T. maritima topo I in a step-wise fashion at a force F ∼ 2 pN in 0.25 mM MgCl₂ (Fig. 5 A and B). To analyze the distribution of step-sizes, we fitted the raw data to a series of steps of amplitude S, occurring at times t_S, constrained by averaging to a minimum time interval t_av (shown in red in Fig. 5 A and B). For seven experiments with E. coli topo I over a force range of 1–2 pN, the best fitted steps were binned (Fig. 5C), and the peak was fitted to a 〈|ΔLk|〉 = 1.03 ± 0.01 (n = 610). The result of an analysis limited to a single force (2.0 pN, shown in the insert) yielded 〈|ΔLk|〉 = 0.97 ± 0.03 (n = 90).

Fig 5.

Step-wise relaxation of (+) supercoiled DNA. The DNA contained a symmetric mismatch of 12 nucleotides. (A and B) Single relaxation events observed in supercoil removal by (A) E. coli topo I (F = 2.0 pN) and (B) T. maritima topo I (F = 1.5 pN) in 0.25 mM MgCl₂. The blue points are the raw data, and the red lines are the best-fitted steps. (C) Probability distribution of E. coli topo I step-sizes (n = 610) in seven experiments with forces ranging between 1.0 pN and 2.0 pN. The data were fit to a Gaussian to yield an average value of 〈|ΔLk|〉 = 1.03 ± 0.01. (Inset) Results from a single experiment at 2.0 pN (n = 90); peak fitted to 〈|ΔLk|〉 = 0.97 ± 0.03.

Therefore, the overwhelming majority of steps corresponded to |ΔLk| = 1. However, even under these conditions we occasionally saw steps corresponding to |ΔLk| ≥ 2. These larger steps might occur because topo I is able to remove supercoils in steps greater than 1. Alternatively, two or more independent step-of-one events could occur on a time scale faster than our temporal resolution. This question was addressed by examining the kinetics of relaxation by E. coli topo I.

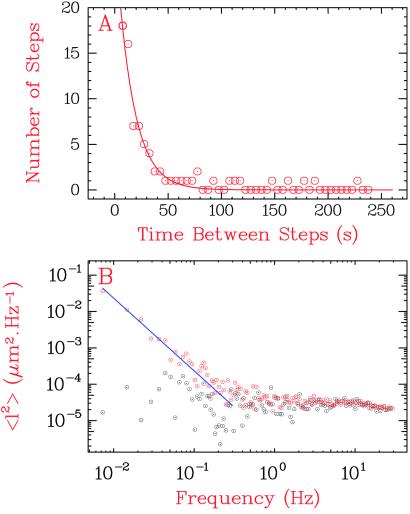
The distribution of time between successive steps of relaxation at F = 2.0 pN is shown in Fig. 6A. These data are well fit by a Poisson distribution with a mean time τ = 15.4 ± 3 s. The Poissonian nature of relaxation events indicates that the applied force acts on a single rate-limiting step of topo I's enzymatic cycle. Furthermore, the exponential fit predicts that 15 ± 3 steps-of-one would occur on time scales faster than our temporal resolution t_av (see Materials and Methods). This result agrees well with the 17 observed fast steps-of-one contained in events contributing |ΔLk| ≥ 2 at F = 2.0 pN (Fig. 5C Inset). We conclude that all steps of |ΔLk| ≥ 2 can be interpreted as rapid successions of single steps, supporting the strand-passage model.

Fig 6.

Kinetic analysis of E. coli topo I at a force of 2.0 pN. (A) Histogram of times between steps in topo I activity, obtained by fitting the data in the Fig. 5C Inset over a time window t_av, where t_av was allowed to vary between acquisitions. The exponential fit yields an enzymatic turnover time, τ, of 15.4 ± 3 s, corresponding to a mean rate of DNA elongation, 〈v〉, of 2.27 nm/s. From this fit, we estimated that topo I performed a total of 15 ± 3 steps in a period faster than our time resolution t_av. This result agrees well with the 17 fast steps-of-one contained in events contributing 〈|ΔLk|〉 ≥ 2 (Fig. 5C Inset). To count these fast steps, a cutoff of 〈|ΔLk|〉 = 1.5 was applied to the Gaussian distribution of the data. (B) Examples of the spectral distributions of the fluctuations of DNA extension obtained with (red) and without (gray) topo I. The difference between these two curves was fit to the function A/f² (blue curve), where f is the frequency and A is the amplitude. A is related to the enzymatic rate v and the step-size S (in nm) by A = Sv/2π². From an average of over eight spectral distributions, we determined a value of 〈A〉 = 4.30 nm² Hz. By using the mean velocity 〈v〉 = 2.27 nm/s, we deduced a step-size 〈ΔLk〉 = 1.07 ± 0.23.

The experiments described above were conducted at a limiting concentration of MgCl₂. It is conceivable that the observed step-of-one behavior is an artifact of reducing the rate, as the limiting value of n is, of course, 1. To analyze the topo I step sizes at much higher reaction rates we used a second, independent method based on analysis of the power spectrum of the fluctuations of the DNA extension, l(t) (26, 27). In this method, the square of the amplitude of the Fourier transform of this signal is analyzed as a function of frequency. An attractive feature of the fluctuation analysis is that information about topo I behavior can be extracted without averaging the data. In the absence of topo I, the amplitude of the Brownian fluctuations of the magnetic bead did not vary as a function of the frequency of the fluctuations (Fig. 6B, gray dots). However, in the presence of enzyme, the random nature of the time between steps of supercoil relaxation caused the fluctuations to increase at low frequencies as A/f², where f is the frequency and A is the amplitude (Fig. 6B, red dots). If the distribution of times between steps is Poissonian, the magnitude A of these fluctuations is related to the enzymatic rate v and step-size S by A = Sv/2π². Thus, analysis of the fluctuations in the experimental signal permits one to deduce the enzymatic step size from a knowledge of its mean velocity. At low rates (〈v〉 = 2.27 nm/s; i.e., an enzymatic cycle of about 15 s; see Fig. 6A), we calculate that 〈ΔLk〉 = 1.07 ± 0.23, which is in agreement with the result obtained from our real-time analysis and reconfirms that the statistical behavior of topo I follows a Poisson distribution. Moreover, the fluctuation analysis can equally well be applied to relaxations under conditions (F < 1 pN and 3 mM MgCl₂) in which a 10-fold increase in topo I relaxation rate prevents real-time determination of steps. If we assume a Poisson distribution, the analysis yields a value of the step-size 〈|ΔLk|〉 = 0.98 ± 0.2. We conclude that our measurement of the enzymatic step size is independent of the means used to slow down topo I activity.

We applied the same analyses to relaxation by T. maritima topo I and found again that 〈|ΔLk|〉 was uniquely equal to one (data not shown). The distribution of step sizes obtained from real-time analysis fit to a Gaussian distribution centered at a 〈|ΔLk|〉 = 1.01 ± 0.02 (n = 213). The histogram of the times between successive steps (averaged over a time window t_av = 1 s) fit an exponential (Poisson) distribution with mean τ = 4 s. We found that the number of steps-of-one predicted to occur on time scales faster than our temporal resolution, 13 ± 4, was in agreement with the measured number of 12 fast steps-of-one contained in events contributing a |ΔLk| ≥ 2. This result shows that, as with the E. coli enzyme, the number of steps contributing |ΔLk| ≥ 2 is completely consistent with the strand-passage model. Analysis of the power spectrum of the fluctuations of T. maritima topo I activity yielded a step-size of 0.97 ± 0.3, which is in excellent agreement with real-time analyses.

Conclusions

Our kinetic data along with past structural and biochemical results (9, 12–14) allow us to conclude that both E. coli and T. maritima type IA topoisomerases use an enzyme-bridged, strand-passage mechanism. Because these enzymes differ greatly in sequence, and the evolutionary divergence of these bacteria is large, it seems safe to conclude that the mechanism is conserved throughout type IA enzymes. This mechanism requiring enzyme binding to a single strand of DNA is well suited to the physiological roles of the two major type IA enzymes, topo I and topo III. Topo I is dedicated to removing (−) supercoils and thus complements DNA gyrase, which removes only (+) supercoils, in maintaining the proper level of (−) supercoiling in bacteria (1, 2). Topo III does not play a role in relaxation of (−) supercoils in either prokaryotes or eukaryotes, but instead probably disentangles single strands produced during replication or recombination by the action of a DNA helicase (15, 16). The rotation mechanism proposed for type IB enzymes is much less controlled and is suited instead to the rapid removal of both (−) and (+) supercoils. The latter activity is required during DNA replication. The rotation mechanism cannot mediate disentanglement, (de)catenation, or (un)knotting of DNA as does the strand-passage mechanism of type IA enzymes. When type IB enzymes carry out such reactions, another mechanism must be coming into play. There is a clear structural similarity between type II and type IA, but not type IB, topoisomerases (28). Because type II enzymes use an enzyme-bridged mechanism, it is clear that the similarity extends to the fundamentals of catalysis. Indeed, we can view a type II topoisomerase as one in which there is concerted type IA action on both strands of the double helix. Finally, we note that our study depended critically on the advantages of single molecule enzymology over ensemble studies. We capitalized on the ease of generating (+) supercoils, the application of force to bring enzyme rate and noise within bounds, and the quantification of fluctuations in the behavior of individual enzymes to calculate step sizes.

Abbreviations

• topo I, topoisomerase I