Predicting the effects of climate change on avian life-history traits

Abstract

Across North America, tree swallows have advanced their mean date of clutch initiation (lay date) by ≈9 days over the past 30 years, apparently in response to climate change. In a sample of 2,881 nest records collected by the lay public from 1959 to 1991, we examined whether clutch size has also responded to climate change. We found that clutch size is strongly related to lay date, both within and among years, and there has been no significant temporal variation in the slopes or intercepts of the clutch-size/lay-date regressions. As a consequence, we expected increases in clutch size with advancement in lay date; however, we detected no such trend over time. The distributions of egg-laying dates were more constricted in the warmest (and earliest) years, suggesting that changes in mean clutch size might be constrained by changes in the distribution of laying dates. If spring temperatures continue to increase, we predict further reductions of variance in laying dates and relatively small increases in clutch size. Such constraints on life-history variation probably are common and need to be considered when modeling the effects of climate change on reproduction in natural populations. Predicting the long-term effects of constraints and interpreting changes in life-history traits require a better understanding of both adaptive and demographic effects of climate change.

Over the past century, global surface temperature has increased by an average of 0.6°C (1). It is now widely accepted that air temperatures have been increasing as a result of increased anthropogenic carbon dioxide in the atmosphere. Air temperature could be one of the key environmental cues affecting the seasonal timing of egg laying in birds, and there is evidence that increases in mean temperatures have led to earlier lay dates in birds (2–6) and accelerated phenologies in many other taxa (7–9).

One of the most general patterns in the life histories of birds is that females that lay later in a breeding season tend to lay smaller clutches (refs. 10 and 11, but see refs. 12 and 13 for exceptions in multiple-brooded species), raising the possibility that earlier breeding may be leading to larger clutches being laid. Clutch size is an important life-history trait, because it sets a hard upper limit on offspring production. It is also the easiest life-history trait to measure, and data on clutch size variation often are available when data on other life-history traits are not.

There is considerable evidence that the correlation between lay date and clutch size may be the result of a strong biological coupling (7, 14), yet the nature of this biological link is very poorly understood. In an early attempt to study this connection between lay date and clutch size, von Haartman (15) suggested a dichotomy in the way that birds adjust their clutch sizes to the timing of breeding. At a study site in Lemsjöholm, Finland, both pied flycatchers (Ficedula hypoleuca) and starlings (Sturnus vulgaris) laid smaller clutches as each breeding season progressed. However, when examined across years, pied flycatchers averaged larger clutches in the years that they began laying earlier, whereas starlings had the same mean clutch size every year regardless of lay date. Thus, clutch sizes of starlings were determined apparently by the date of laying relative to the mean for the population, not, as in the flycatcher, to the absolute date that they laid; the earliest starlings laid the same number of eggs, regardless of the calendar date of their clutch initiation.

In the period from 1959 to 1991, the lay date of tree swallows across North America shifted an average of 9 days earlier (6). This shift provides an opportunity to assess the impact of climate change on tree-swallow clutch size and to begin to examine the mechanisms underlying life-history responses to environmental changes by evaluating the relative and absolute modes of clutch-size response suggested by von Haartman (15). We have taken a general approach to testing the relationship between lay date and clutch size, first evaluating the appropriate measures of lay date, then investigating further the relationship between lay date and clutch size. Differences in clutch size could arise because (i) lay dates do not change, and the relationship between clutch size and lay date does change, (ii) lay dates do change, and the relationship does not, or (iii) because both lay dates and the lay-date/clutch-size relationship change. Our analyses have been designed to test all three of these possibilities.

Materials and Methods

The Data.

The results reported here come from analyses of 40 years (1952–1992) of data from over 21,000 nest records supplied by volunteer programs that collect nesting records from throughout North America. This is the same overall data set analyzed previously (6, 16).

All records used in this study came from nest boxes, and thus it is unlikely that any temporal or geographic changes were due to differences in nest-site selection. Also, tree swallows are single-brooded in the range covered by our sample (17), and thus our results are not influenced by clutch-size differences in second broods. We used only records with at least two visits to the nest including one during laying (typically mid-May to early June). Visits during laying were identified by an increase in the number of eggs on subsequent visits. Clutch size was measured as the maximum number of eggs observed in the nest. We did not use records from known renests or clutches with fewer than three eggs (n = 43 clutches) or more than eight eggs (n = 26), because these nesting attempts were likely to have been abandoned early or produced by two females nesting in the same nest box, respectively (D.W.W. and P.O.D., unpublished observations). Lay date (date of clutch initiation) was estimated to within 1 day by back-dating one egg per day from the date of the first record of eggs in the nest.

Our final data set included 2,881 clutches from 1959–1991. Years with fewer than five nest records (1952, 1955–58, 1960, 1964–65, and 1992) were eliminated, and the mean number of nests per year was 115 (range = 6–280; all but 5 years had n ≥ 20). These records span most of the normal breeding range of tree swallows; no data were available from Newfoundland and Alaska (16).

We compiled surface air temperatures during breeding for each clutch in the year and location it was laid. Mean temperatures in April and May (before and during laying) were estimated for each year and 1° block of latitude and longitude (latilong) for which we had nesting data. Within each latilong block we compiled mean April–May temperatures and elevation from all weather stations in the Global Historical Climatology Network, version 2 (18). On average, data were available from 2.4 weather stations within each yearly latilong. We found previously that laying date was earlier in locations with more swallows (6), and thus to avoid any confounding effects we also included density in our analyses. Tree-swallow density was estimated by using abundance indices from the Breeding Bird Survey program of the U.S. Fish and Wildlife Service (6). Density estimates were averaged for each latilong block by using data from multiple surveys and years where available (mean per latilong = 4.3 routes and 76.7 total survey years).

Statistical Methods.

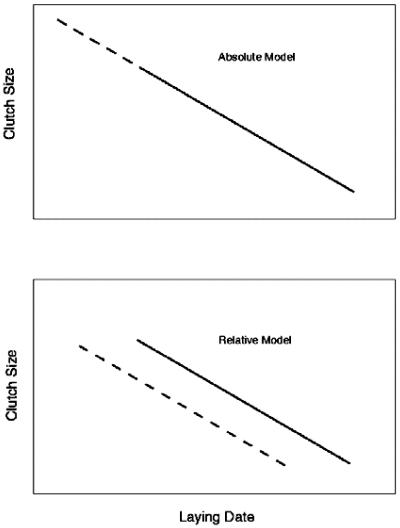
To test precisely between the absolute and relative modes of the clutch-size/lay-date relationship (15), we decomposed the effect of lay date into the effect of the mean lay date for a given year and the deviation of any particular clutch from that annual mean. If clutch size is influenced by relative lay date only, then only the lay-date deviation will have a nonzero coefficient, and the mean lay date coefficient will be zero. If both enter the model with equal coefficients, then the two can be combined into a single, absolute lay-date contribution (Fig. 1).

Figure 1.

An idealized representation of the relationship between clutch size and lay date under absolute and relative modes of clutch-size determination (after von Haartman, ref. 15). In the absolute mode, clutch size responds to lay date such that a change to an earlier lay date (e.g., in response to warming) would result in larger clutches being laid, with the population shifting up the same regression line (dashed portion). Under the relative mode, earlier lay dates would result in a shifting to the left of the clutch-size/lay-date regression without any shift in mean clutch size. Note that these simplified graphs assume constancy of the regression slope with changes in lay date.

Once we determined what model of lay date was most appropriate, we analyzed annual variations in the clutch-size/lay-date regressions by conducting tests of differences in the slopes and intercepts of these regressions across years. For all our analyses, we used the procedure “MIXED” in SAS (19). Tests are provided by the “COVTEST” option in MIXED, and we specified random effects for “intercept” (a reserved term for SAS) and lay date, with categorical year designated in the “SUBJECT =” option for the random effects. This insures that a separate random effect for the slope and intercept of the clutch-size/lay-date regression be fitted for each year. To clarify the interpretation of these regressions, we centered the fixed effects of year and lay date around the mean year (1982) and lay date (June 5, Julian day 155) by subtracting these quantities from all years and lay dates, respectively. All analyses presented here incorporate these year and lay-date centerings.

Once issues of lay-date measurement and the constancy of the lay-date/clutch-size regression were addressed, we analyzed the linear and quadratic fixed effects of other potential environmental predictors of clutch size in conjunction with the female's lay date.

To correct for the effects of small sample sizes in some of the strata of our data, we specified the “ddfm = kenrog” option on the “MODEL” statement to obtain Kenward–Roger estimates of the denominator degrees of freedom (df) for the tests of fixed effects (20). Because large data sets that are collected ad lib have variable problems of nonindependence, we corrected for the spatial correlation of data points by including a categorical “zone” as a random effect in the analyses. Zone is an arbitrary designation of the latilong block for each data point, and because it was treated as a categorical variable, it represents only contiguity not the directional information inherent in the latitude and longitude predictors included as fixed effects. We made a similar allowance for the effects of temporal correlations by including a categorical year variable as a random effect, retaining the continuous year as a fixed effect to test for any linear trends across years in clutch size. We also ran analyses without categorical year as a random effect to be sure that the variance accounted for by the random effect was not robbing year as a fixed effect of explanatory power. None of these analyses without the random effects of year vary qualitatively from those presented here.

The significance of the random effects was tested by running the mixed model with and without each random effect (in this case categorical year, geographic zone, or the year × lay-date slopes and intercepts) and then comparing −2 × the residual log likelihood for the analyses with and without the random effect of interest. This difference in residual log likelihood (the DRL) was compared with a χ² with 1 df by using a table value at twice the nominal significance level (e.g., by using α = 0.10 critical values to conduct a 0.05 level test; ref. 21, p. 63). These significance tests generally are more reliable than the Z test provided by MIXED (ref. 22, p. 491).

For a more comprehensive visualization of the effects of environmental changes on both lay date and clutch size, we conducted a path analysis (e.g., 23) to evaluate the relative strength of the direct and indirect effects of lay date and annual variation on clutch size.

Results

There was strong support for the absolute model of lay-date response in tree swallows. The effects for both the mean lay date (P = 0.015) and the deviation from the mean lay date (P < 0.001) were significant, and the values of the coefficients for the two effects (−0.027 and −0.031, respectively) were remarkably similar. A contrast to test the difference between these two was definitively not significant (P = 0.714). Clearly, both the annual mean lay date and an individual clutch's deviation from that mean are important to clutch-size determination. We thus accepted the absolute model of lay-date/clutch-size relationship, and in all further analyses we present the lay-date effect in its raw absolute, but centered, form.

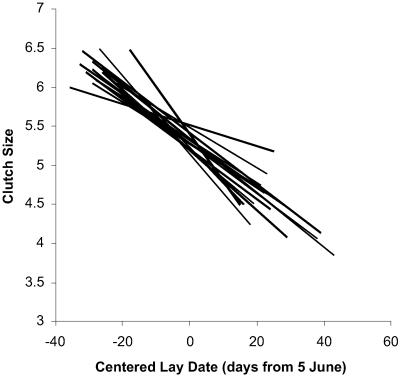
To explore whether the clutch-size/lay-date relationship was variable from year to year, we ran MIXED with separate variance estimates for the random effects of slopes and intercepts. We found that the estimated variance for the slopes was virtually zero (<10⁻⁵), and thus we dropped the random effect for the slope of lay date from our model, fitting only the intercepts for the clutch-size/lay-date regressions for each year's data. When this simplified model was re-run, the tests of random effects indicated that there were significant effects of geographic zone (DRL = 15.6, P < 0.001) and marginally nonsignificant effects of year (DRL = 2.3, P = 0.065) on clutch size. (A set of analyses that included quadratic fixed effects (see below) yielded qualitatively identical results). This result indicates that indeed there were nondirectional effects of both space and time on clutch size, although the effect of random spatial variation was much stronger than the effect of random annual variations. Plots of the regressions of clutch size on lay date for each of the 17 years that had significant regressions (Fig. 2) show the remarkable similarity in slopes and minor variation in intercepts across years. A similar analysis exploring the possibility of geographic variation in the lay-date/clutch-size regression found no effect of the latitude × lay-date or longitude × lay-date interaction nor of the latitude × longitude × lay-date interaction on clutch size.

Figure 2.

The corrected regressions between clutch size and date of egg laying (clutch initiation) for the 17 years from the sample that had slopes significantly (P < 0.05) different from 0. These are estimates of clutch size corrected for all the other covariates in Table 1 by forcing SAS to calculate separate intercepts and slopes for each year as fixed effects. Each regression line is drawn only to the limits of the data set for each year. Note the similarity of observed slopes and the relatively minor differences among the regression intercepts across years.

As useful as the random effect tests are in and of themselves, the other great advantage of mixed model analysis is its ability to provide tests of the fixed effects with the effects of nonindependence due to variation in the random effects controlled for in the analyses. We evaluated the following potential fixed effects on clutch-size variation: lay date, year, latitude, longitude, April–May temperature, elevation, and tree-swallow density. We included squared predictors for all fixed effects to investigate nonlinear relationships, as well as all two-way interactions of both linear and quadratic predictors between lay date, temperature, and year, and between temperature, latitude, and longitude. To clarify interpretation of regression coefficients, fixed effects were centered on their overall mean before conducting the analysis. The resulting “full” model was simplified by backward elimination of fixed effects, one at a time, in decreasing order of their P values until all fixed effects had a P value of no larger than 0.15. One of the most important fixed effects to evaluate is that of year, to test for a regular annual trend in clutch size that parallels the decrease across years in lay date (6). Despite the marginally significant (P = 0.065) random variation in the intercepts of the clutch-size/lay-date regressions, there was no significant trend toward larger clutch sizes with year (P = 0.358) once other related and nonsignificant predictors were removed from the model.

The lack of a trend toward larger clutches is in contrast to a very strong effect of lay date on clutch size. As in other studies of tree-swallow breeding biology (e.g., refs. 11, 16, and 24), the very strong effect of lay date on clutch size was negative: For every day later that a bird began laying, its final clutch size averaged 0.03 fewer eggs (Table 1). The overwhelmingly strong linear effect of lay date is joined by a weaker quadratic effect, producing an accelerating decline in clutch size with lay date. These results also indicate that clutch size increases linearly as one moves north and to higher altitudes and decreases quadratically as one heads west across the species' range (Table 1).

Table 1.

Results for the fixed effects from mixed-model analysis of each of the indicated predictors on clutch size

Effect	Estimate	Standard error	KR degrees of freedom	t value	P
Intercept	5.5537	0.04432	54.9	125.32	<0.0001
Laydate	−0.02956	0.001884	2,649	−15.68	<0.0001
(Laydate)2	−0.00022	0.000109	2,722	−2.03	0.0421
Latitude	0.05036	0.009067	49.5	5.55	<0.0001
(Latitude)2 × April–May temperature	−0.00101	0.000402	236	−2.50	0.0129
(Longitude)2	−0.00043	0.000097	60.7	−4.45	<0.0001
(Longitude)2 × April–May temperature	0.000047	0.000028	75.2	1.66	0.1019
Elevation	0.000383	0.000073	49.7	5.27	<0.0001

All predictors in this analysis were centered around their overall mean before the test. Degrees of freedom are estimated for each predictor with the Kenward–Roger (KR) procedure. For details on model simplification see Results. 

It is interesting that the only effects of Spring temperatures on clutch size are in their interactions with latitude and longitude (Table 1). When April–May temperatures were forced back into the model of Table 1, their main effect remained nonsignificant (P = 0.358), and the significance of all fixed effects in Table 1 remained the same. Tree-swallow density also varied substantially in our data set, and the lack of any density dependence on clutch size contrasts to the negative effect of density on timing of breeding (6). One way to explain the lack of a significant effect of Spring temperatures (and through temperatures, year) on clutch size, is that some constraint on earlier laying limits the ability of birds to continue to shift their lay date and clutch size in response to warmer Springs. To test this possibility, we used MIXED to test whether warmer Springs had not only earlier lay dates (6) but also lower variance in lay dates. We did this by dividing the years into quartiles on the basis of the mean Spring temperatures of the records in each. We then used dummy variables for quartile membership as random effects to evaluate differences in lay-date variances across years. This analysis showed that the lowest variance in lay dates occurred in the warmest quartile of years. There was a significant increase in the variance of lay date when we compared the warmest quartile of years with the rest (DRL = 5.4, P = 0.010). We interpret this lower variance in the warmest years as evidence that there may be some constraint preventing birds from laying earlier, causing more individuals to “pile up” in the early end of the lay-date distribution.

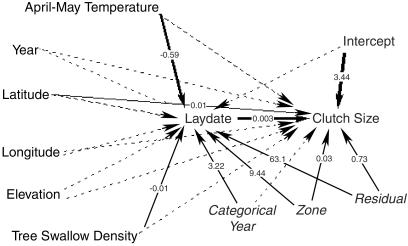
This constraint may explain the lack of any effect of temperatures and years on clutch size, because the birds seem to be making their important reproductive decisions based on lay date and adjusting clutch size to that. This interpretation is reinforced visually by a path analysis (Fig. 3). The path analysis crystallizes the picture of the remarkably simple interactions of environmental factors with clutch size and lay date. Lay date is related very strongly to variation in Spring temperatures (in all but the warmest Springs), and clutch size is affected strongly by lay date. The absence of robust effects of other environmental factors on lay date or clutch size predicts a simple mechanism by which the environment affects lay-date variation, which in turn drives variation in clutch size. Although Spring temperatures do not have a significant direct effect on clutch size, the indirect effect through lay date is very strong. The fact that tree swallows seem to be absolute-date layers (i.e., that their clutch sizes seem to respond both to annual mean lay date and individual deviations from that mean) would suggest that further warming of global climates will effect an increase in clutch size if and only if lay date continues to respond.

Figure 3.

A path analysis summarizing the main effects of all linear predictors, without interactions, on lay date and clutch size. Dashed arrows are for effects that are not significant (P > 0.05), with denser dashing for two effects with 0.10 > P > 0.05. Significant effects are designated by solid arrows, with heavy arrows for effects with P < 0.001. For significant effects, the standardized coefficients from the tests of fixed effects are presented along the arrow. For random effects (in italics), the numbers on the significant paths represent the raw covariance parameters estimated by the procedure MIXED. For simplicity of presentation, we omitted all interaction and quadratic terms from the path diagram. For further details see text.

Discussion

Across North America, tree swallows show extraordinarily little variation in the relationship between clutch size and timing of breeding. The marginally nonsignificant random effect of year on the intercepts of this regression (DRL, P = 0.065) indicates that there certainly is some variation across years in the relationship, but the strong effect of both the annual mean lay date and the individual deviation from that mean on clutch size indicates that the random effect must be due to other causes. In any event, it is striking how little this relationship varies in slope. It is seldom in a data set this size that the variation in a variable is so slight that the random effect for that variable yields variance estimates <10⁻⁵. It is hard to see why this regression's slope is not influenced more strongly by the differences in ecological conditions that produced strong differences in lay date (6), and the constancy of slope suggests the role of some deeper organismal processes in addition to environmental effects. In any event, this constancy of slope, together with the fact that tree swallows respond to both the annual mean lay dates and their deviations from those means when deciding how many eggs to lay, indicates that they indeed are traveling up and down the same regression line in making their clutch-size decisions. Thus, among the three possibilities suggested in the Introduction, it seems that both lay dates and the lay-date/clutch-size relation have changed, but the former have changed much more than has the latter.

Our focus here has been on environmental conditions immediately preceding laying. There remains the possibility that conditions on the wintering grounds (25) or even in the previous year's breeding attempt (26) could affect laying date and thus clutch size. However, longitudinal studies of known individuals have revealed very few carryover effects of previous reproductive attempts in tree swallows (27–29); indeed, all available evidence suggests that tree swallows are income breeders (11) that base their reproductive decisions on current environmental and physiological conditions.

Our results present an interesting paradox, because we had expected clutch size to increase with the warmer temperatures of more recent years. One explanation could be that the clutch-size/lay-date relationship has remained unchanged and the lack of a clutch-size effect is due to a constraint on earlier lay dates. Perhaps changes in temperatures cause only the later-laying females to advance their laying and increase their clutch size, whereas the earliest laying females neither advance their laying nor increase their clutch size. This scenario is supported by the fact that birds in this study in warmer years exhibited reduced variance in lay dates; however, this reduced variance could be imposed also by a constraint on clutch-size increases. Alternatively, the clutch-size/lay-date relation may be flexible, and clutch size may have independent upper limits that are determined by factors other than lay date. Such flexibility may have a parallel with the diversity of responses of birds to food-supplementation experiments early in Spring (e.g., refs. 30 and 31), with some species changing both lay date and clutch size (e.g., refs. 32 and 33) and many more changing only lay date (e.g., ref. 34). Focused studies of annual variations in food supplies, temperatures, and lay dates are needed. But no matter what future research uncovers about the relationship between lay date and clutch size, the present study clearly shows that a lack of change in clutch size with annual changes in mean lay dates cannot be taken alone as strong evidence for the relative mode of lay-date response (15).

Even if continued global warming does indeed lead to larger clutch sizes, it is not clear what exactly those changes would mean for tree-swallow populations. Although it is possible that increased egg laying might impose extra costs on the laying females, these birds seem to be income breeders (11, 35, 36), and the costs of increased clutch size are not likely to be great (37). Much more likely would be the costs that may accrue to parents rearing larger numbers of young, but here too, considerable experimental evidence suggests no large brood size-dependent costs of reproduction in this species (27–29). The largest costs may be borne by the offspring, which may suffer longer nestling periods or smaller fledging weights and reduced postfledging survival as the result of larger brood sizes.

There is also a large number of other life-history traits (e.g., parental and offspring survivorship, offspring growth rate, migration, and dispersal) that are either known or suspected to be affected by lay-date variation. An assessment of the net effects of global change must await a thorough analysis of its effects on many of these other factors. Unfortunately, all these other life-history traits are not as simple to measure as is clutch size, and information on them is not available over such a large temporal and spatial scale. Measures of long-term changes in life-history traits other than clutch size must await detailed studies conducted at a variety of sites across the tree swallow's range.

Not only may other life-history traits be affected by climate change, but further climate change also may have adverse effects on the match between food for chick rearing and chick-rearing dates. Birds frequently lay eggs using a food supply that is different from that on which they feed their young. It is generally thought that the food supply for the developing young is the most important resource for breeding and is the selective factor to which timing of breeding is adjusted by selection (e.g., refs. 38–40). This adjustment can rely on a variety of cues, and it is very difficult to predict when temperature effects on those cues may cause a mismatch in the timing of offspring food availability and the timing of chick hatching (e.g., ref. 41). Alternatively, even if the cues continue to time reproduction correctly, ectothermic prey may initiate development at the “right” time for the birds, but their development is likely to be sped up much more than is that of the homeothermic nestlings, and the food supply may not last the entire developmental period of the nestlings (39, 42). Both and Visser (43) recently suggested that migratory birds may be especially vulnerable to such mistiming, because their return to the breeding grounds may be cued by photoperiod, whereas the phenology of their resident prey advances as a consequence of global warming, leaving the birds behind their prey from the moment they return from the wintering grounds. Although this is a potentially important effect of global change that must be taken into account, it is unlikely to affect tree swallows for some time, because they typically return to the breeding grounds to secure nesting cavities 3–6 weeks before laying commences. Given the diversity of invertebrate responses to climate change (e.g., ref. 44), it seems likely that the avian insectivores least affected by climate change will be those with the greatest diversity of suitable prey for egg laying and chick rearing.

In making assessments of the impacts of environmental change on avian populations, it is important to distinguish between what might be called adaptive and demographic effects. Visser et al. (41) showed how the mismatch between the timing of great tit breeding and the abundance of the tits' prey led to selection gradients for earlier breeding in the tits. However, selection gradients for earlier breeding do not necessarily mean that the population is declining or is at risk of doing so in the future. Indeed, tits that breed earlier and have a reproductive advantage in terms of greater production of offspring might have that advantage eliminated by increases in the mortality of offspring (e.g., refs. 45 and 46). Scientists wishing to assess the potential negative effects of climate change must consider not only whether selection might be pushing the population in different directions but also whether the predicted changes are likely to have tangible effects on the population sizes or dynamics (e.g., ref. 47) of the species of concern.

Abbreviations

latilong

1° block of latitude and longitude

DRL

difference in residual log likelihood