Simulation of non-specific protein–mRNA interactions

Abstract

Protein–nucleic acid interactions exhibit varying degrees of specificity. Relatively high affinity, sequence-specific interactions, can be studied with structure determination, but lower affinity, non-specific interactions are also of biological importance. We report simulations that predict the population of nucleic acid paths around protein surfaces, and give binding constant differences for changes in the protein scaffold. The method is applied to the non-specific component of interactions between eIF4Es and messenger RNAs that are bound tightly at the cap site. Adding a fragment of eIF4G to the system changes both the population of mRNA paths and the protein–mRNA binding affinity, suggesting a potential role for non-specific interactions in modulating translational properties. Generally, the free energy simulation technique could work in harness with characterized tethering points to extend analysis of nucleic acid conformation, and its modulation by protein scaffolds.

INTRODUCTION

Non-specific interactions between protein and nucleic acid are important determinants of biological function, e.g. in combining with specific interactions to form distorted binding geometries (1) or facilitating reduced dimensionality searches for binding sites (2). Major questions remain to be resolved concerning packaging and unpackaging of nucleic acids in many systems, including chromatin (3) and viruses (4). Structural biology provides much information about specific protein–nucleic acid complexes (5), including the ribosome (6), whilst atomic-level molecular models can be used in relatively short simulations (7). It has been apparent since the first structure determinations for nucleic acid binding proteins that surface charge plays a significant role in binding. This property is currently being used to aid the identification of DNA-binding surfaces in proteins emerging from Structural Genomics initiatives (8,9), and in studies of DNA wrapping paths around proteins (10). Methods for computational analysis of protein–nucleic acid interactions at a reduced level of complexity are being introduced (11,12).

The mRNA cap-binding protein eIF4E has central roles in several aspects of post-transcriptional gene expression (13). In cap-dependent translation initiation, eIF4E binds the mRNA cap before ribosome docking, in a larger complex that includes eIF4G (14). Transport of mRNAs from the nucleus also make use of the capped mRNA-binding potential of eIF4E (15). The cap binds to a groove in eIF4E, an interaction which is modulated by a variety of binding partners (16) that contact a region on the opposite side of eIF4E to the cap site (17). The molecular mechanism of interaction between these binding sites is not yet fully understood. Binding of a fragment of eIF4G (393–490) triggers a coupled folding event with the eIF4E N-terminus (18). There is no major structural change at the cap site, although some chemical shift changes may relate to modulation of binding affinity (19). Interaction between the two sites can occur with cap in the absence of an mRNA body, demonstrated for eIF4G fragments (19), and with a substantial reduction in cap analogue binding upon eIF4E association with a number of factors, including promyelocytic leukemia protein (20). Interactions between mRNA and eIF4E have also been studied in the absence of additional factors. Although NMR measurements of eIF4E binding to capped trinucleotide RNAs show no detectable contacts beyond the first nucleotide following the cap structure (21), sequence alteration close to the cap causes variation in affinity (22), presumably due to non-specific protein–RNA interactions. Studies of eIF4E association with cap analogues of varying phosphate chain length, with changes in ionic strength and with engineered protein surface charge to mimic phosphorylation events (23), indicate that electrostatic interactions are important in this system (24). Brownian dynamics simulations have been used to interpret the salt-dependence of cap-eIF4E binding (25).

We report a Monte Carlo simulation approach, using a type of ‘phase switch’ algorithm (26), which allows prediction of the free energy difference between two systems, as opposed to the intractable problem of deriving free energy for a single system in isolation using Monte Carlo. The ‘phase switch’ method is used with a coarse-grained RNA model and either free or eIF4G-bound eIF4E. The presence of the eIF4G fragment is predicted to have a small, but significant effect (via non-specific interactions) on capped mRNA-binding, accompanied by alteration of the preferred pathways of mRNA in the simulations. We further investigate alteration of surface charge for two modelled Schizosaccharomyces pombe eIF4Es (27).

MATERIALS AND METHODS

In our calculation scheme, eIF4E protein and eIF4E complexed to an eIF4G fragment (18) are modelled as fixed units with impenetrable volumes. The eIF4E protein alone was trimmed down to that part which is structured in the absence of eIF4G (17). Each protein unit is surrounded by a fixed electrostatic potential field, calculated with the Finite Difference Poisson Boltzmann (FDPB) method (28). Ionisable group charge was assigned at neutral pH with model compound pK_as (29), and 0.15 M ionic strength was used. The mRNA chain is modelled as a chain of tangent hard spheres, diameter σ = 7 Å (i.e. nearest neighbour bond length fixed at 7 Å), each monomer carrying a charge of q = −1e, where e is the proton charge. Non-bonded monomers interact via the hard-core screened Yukawa potential, given by:

$$u\left(r\right)=\{\begin{array}{cc}\infty & r\le \sigma \\ -\frac{q^2\sigma }{4\pi \varepsilon \varepsilon or}\text{exp}\left(-\kappa \left(\frac{r}{\sigma }-1\right)\right)& r>\sigma \end{array}$$

with an inverse screening length κ due to counterions that matches the FDPB calculations of protein electrostatic potential, and dielectric constant ɛ = 78.4 for the solvent, with ɛ₀ the vacuum permittivity.

We have performed simulations for single free hard core Yukawa chains to calculate the persistence length, l_P, for comparison with experimental results. We have measured the mean end-to-end distance, R_e, for these polymers, and estimated the persistence length via the relationship expected from the Worm-Like Chain model (30,31):

$$〈R_e^2〉=2l_{P}L(1-l_P(1-exp(-L/l_P))/L)$$

where L is the contour length (end-to-end length at full extension) for the polymer. For chains at 311 K, this gives an estimate for the persistence length of 3.1 nm. By comparison, microscopy, single molecule stretching and spectroscopic methods yield experimental results from <1 nm to around 10 nm, for single-stranded RNA and DNA (31–36). The shorter persistence lengths mostly relate to single molecule experiments, and the larger values to bulk measurements.

For our non-specific binding simulations, the model mRNA chain, which is tethered to eIF4E at the cap site, moves within the protein electrostatic potential, discretized on a 2 Å grid. Protein excluded volume is also recognized with a grid map. Standard polymer Monte Carlo moves (37) (crankshaft, pivot and CCB) are used to generate mRNA chain configurations. In addition, every 1000 configurational move attempts a switch move (26) is attempted. This swaps the protein unit with which the mRNA chain is interacting, according to the standard Metropolis Monte Carlo acceptance probability (38), P_acc = min[1,exp(−ΔE/k_BT)], where ΔE is the change in energy for this move. At the end of the simulation, the free energy difference between the two systems can be estimated as ΔG_A→B =−k_BT ln(n_B/n_A), where k_B is the Boltzmann constant, T is the temperature and n_x is the number of sampled configurations where the mRNA was attached to protein unit x. Since the system is held at constant volume (infinite dilution), the enthalpy difference between the two systems, ΔH_A→B, can be estimated as the difference in average interaction energy for each system. This also allows access to the entropy difference between the two systems, ΔS_A→B, since ΔG_A→B = ΔH_A→B −TΔS_A→B. To avoid problems of metastability, simulations are performed within a parallel tempering framework (38), using ten simulation boxes distributed according to a power law across a range in temperature (39). After an initial equilibration run of 5 × 10⁷ move attempts, data collection runs are made over 10⁸ move attempts, with data recorded every 5 × 10⁴ move attempts. During post-processing, a smooth interpolation of data across the studied temperature range is achieved using the multiple histogram method (40). Over the course of each simulation, we record how many times monomer centres lie within each potential map cell, which allows us to build up a probability density map for mRNA configuration.

RESULTS

Non-specific RNA–protein interactions in the eIF4E/4G system

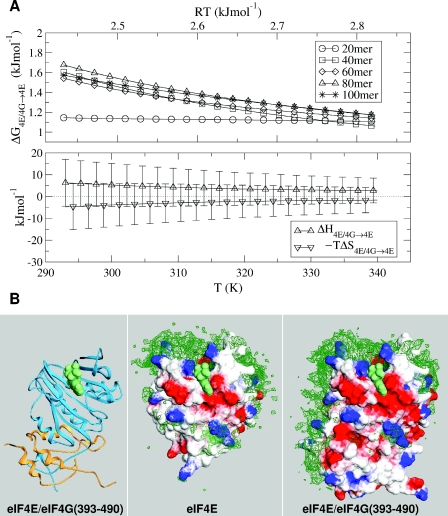
One end of RNA polymer is fixed to eIF4E in all simulations, modelling cap binding (Figure 1). Monte Carlo sampling of RNA polymer conformation is made for two related systems, with a switch move allowing evaluation of the protein–RNA binding energy difference, ΔG, between the two systems. Figure 2A shows the calculated ΔG for mRNA-binding upon addition of the eIF4G fragment (18), with variation in RNA length and temperature. The binding differential saturates as mRNA length is increased to 40 monomers, with a value of 1.5 kJ/mol at 310 K. Although this represents a relatively small impact on a binding equilibrium (a factor of ∼1.8), it is accompanied by a substantial change in RNA paths brought about by eIF4G fragment binding to eIF4E (Figure 2B). A relatively small free energy change coupled to an observable re-distribution in mRNA paths is consistent with a delicate balance of enthalpic and entropic components (Figure 2A).

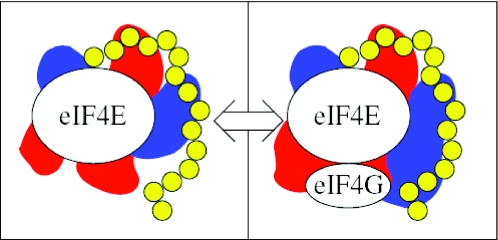
Figure 1.

Simulation schematic. Modelled mRNA (yellow beads) moves within the protein excluded volumes and electrostatic potential fields (red, blue) of the eIF4E and eIF4E/eIF4G fragment systems. Switch moves test the energetics of swapping between these systems.

Figure 2.

Binding of mRNA to eIF4E and eIF4E complexed to an eIF4G fragment. (A) Temperature-dependence of binding differential (ΔG_4E/4G→4E, ΔH_4E/4G→4E, −TΔS_4E/4G→4E), with more favourable binding to eIF4E/4G complex denoted by positive ΔG values. Results (ΔG) are shown for variable polymer length. (B) RNA monomer densities (green) around eIF4E and eIF4E/4G complexes, with electrostatic potential surfaces at −k_BT/e (red) and k_BT/e (blue). The ribbon diagram is colour-coded according to eIF4E (cyan) and eIF4G fragment (orange), with a spacefilled cap analogue in all panels. This figure was drawn with Swiss PDB-Viewer (46).

Differences between S.pombe eIF4E1 and eIF4E2 interactions with mRNA

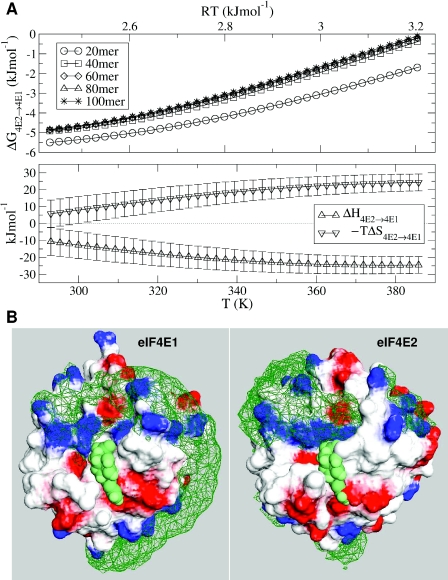
Our analysis has been extended to include two eIF4E homologues from S.pombe, for which we have previously made structural models (41). In this case we use just that part of eIF4E that is structured in the absence of eIF4G, and the binding energy difference is now calculated between the two S.pombe eIF4E isoforms. The binding differential is again saturated at a length of 40 monomers, with binding more favourable for eIF4E1 by about 5 kJ/mol at 300 K, corresponding to a change in binding of around 7-fold (Figure 3A). The extent to which enthalpic and entropic components balance to give a small change in free energy is also evident. Monomer density plots (Figure 3B) suggest that mRNA occupies significantly different conformational space in the two systems. These densities follow the positive protein electrostatic potential, whether this be extended (eIF4E1) or more concentrated in a surface patch (eIF4E2). The mRNA model includes screened monomer–monomer interactions, which generates a stiffness (calculated persistence length of 3.1 nm for free mRNA) that probably contributes to mRNA following elongated paths where these are available (eIF4E1).

Figure 3.

Binding of mRNA to S.pombe eIF4E1/E2. (A) Temperature-dependence of binding differential, with ΔG_4E2→4E1 plotted for variable polymer length. Simulations have been performed up to high (non-physiological) temperatures to facilitate the parallel tempering algorithm in allowing configurations to escape metastable ‘traps’. More favourable binding to S.pombe eIF4E1 is denoted by negative ΔG. (B) eIF4E surfaces with mRNA monomer density plots, as detailed in Figure 2, with spacefilled cap analogue (green).

DISCUSSION

The alteration of surface charge mediated by phosphorylation of eIF4E on S209 may play a role in the control of translation initiation (23), and appears to be involved in regulation of transformation and mRNA transport properties of eIF4E (42). The scale of binding changes that are likely to underpin these physiological effects can be assessed from in vitro measurements. Phosphorylation at S209 gives about a 2.5-fold change for cap analogue binding and 5-fold for capped mRNA (23). Charge mutation at S209 has not been simulated in the current study since this is close to the cap site and would be a less effective probe of non-specific interactions. However the alteration of binding equilibria that we predict for capped mRNA interactions, about 2-fold for eIF4G/eIF4E compared to eIF4E and about 7-fold difference between S.pombe eIF4E1 and eIF4E2, are of the same order as those measured for S209 phosphorylation. We therefore suggest that modulation of protein surface charge could provide a physiologically relevant mechanism for fine-tuning the mRNA-binding affinities of eIF4E variants.

The model excludes several factors that play roles in eIF4E–mRNA interactions, such as possible allosteric changes associated with effector binding to eIF4E (18), additional (sequence-specific) mRNA tethering interactions mediated by some eIF4E-binding proteins (16,43,44), the extent of secondary structure within the 5′-untranslated region (5′-UTR) and RNA helicase activity associated with eIF4A, and poly(A)-binding protein (13). With regard to RNA secondary structure, it is possible that eIF4E surface charge could interact differentially according to the density of RNA negative charge. For example, the less linear concentration of positive charge on S.pombe eIF4E2 relative to eIF4E1 may interact preferentially with more compact/structured mRNA segments. This would be consistent with the observation that the presence of eIF4E2 modifies the competence of S.pombe ribosomes to translate mRNAs with structured leaders (27). Our calculations also suggest that mRNA binding affinity will vary with changes of intracellular salt concentrations that may result from externally applied salt stress (45).

Since we are examining the effects of non-specific mRNA–protein interactions, the complexities of individual nucleotides are replaced with a chain of identical, spherical monomers. The internal (to the nucleotide) degrees of freedom ignored by this model will be approximately the same in the systems between which the free energy differences are being taken; as such, they should make only a small contribution to the measured binding differences. The switch algorithm used to find the free energy differences is entirely separate from the approximations made in the modelling process. In order for the algorithm to function, it is necessary only that the switch move is accepted often enough to give statistically significant sampling of both systems. This type of algorithm has proven useful in the field of chemical physics (26), and has other possible applications in computational molecular biology. The simulations reported here, and related work (12), add quantitative prediction to qualitative arguments based solely on matching of positively-charged protein regions with negatively-charged phosphate backbone. The details of protein surface charge can be incorporated with FDPB calculations, whilst the entropic cost of restraining nucleic acid conformation is included with polymer modelling. This technique is suitable for study of other systems where a nucleic acid molecule is tethered to a protein unit, such as mRNA decapping enzymes. The method can also be extended, (with appropriate revision of nucleic acid model), to duplex DNA-binding systems in which a sequence-specific recognition site is flanked by regions that can form non-sequence-specific contacts with protein. Incorporation of duplex modelling will also allow estimation of the role of nucleic acid secondary structure for interacting systems such as eIF4E and mRNA. Our modelling suggests that a degree of tuning may exist between charged surface shapes of protein and nucleic acid. Bioinformatics analysis of the database of complexes could go beyond positive/negative charge recognition to study underlying patterning. These further developments generally have the potential to enhance computational analyses of proteins of unknown function, particularly when combined with searches for specific binding/tethering sites.