A thermodynamic model of transcriptome formation

Abstract

The genome supplies information on both the quality and quantity of the transcriptome. However, as it remains unknown how a cell determines transcript levels from the genome sequences, despite comprehensive knowledge of the cellular components involved, the quantity information held by the genome cannot as yet be derived from nucleotide sequences. The model presented here explains on a thermodynamic basis how the components decode the genome to form and maintain the transcriptome. The model describes the level of a transcript as a pseudo-equilibrium between velocities of synthesis and degradation, both of which are controlled by sequence-specific interactions between protein factors and nucleic acids. Each of the transcript levels can be described by a single equation expressing a function of the activity concentrations of the protein factors. Quantitative information in the genome can thus be transformed into constants determined from the nucleotide sequences. Using this model, the transcriptome can be traced back to the protein factors and the state of chromosome packaging. The total description of transcript levels allows the model to be verified through comparison of derived hypotheses with comprehensive measurements of the transcriptome. The hypotheses thus derived in the present study are well supported by experimental microarray data, confirming the appropriateness of the model.

INTRODUCTION

Organization of the large volumes of experimental data acquired to date requires an appropriate model to serve as a framework for analysis. The ability of such a model to integrate the data is critical and will affect the accuracy and potential utility of data comparisons. Objectivity is required in the model, particularly when the results are to be shared among researchers, such as for transcriptome analyses. Many transcriptome studies have employed versatile theoretical models for each step of data analysis, including normalization, noise treatment and data interpretation that includes validations for expressional changes (1–5). Unfortunately, in exchange for such versatility, the objectivity of the models is reduced. Some models even rely on arbitrary calculations to eliminate the linear responses of data (5). In general, poor objectivity or linearity prevents meaningful comparisons between multiple experiments, giving rise to inconsistencies among sets of analytical results.

This report presents an objective model that explains the determination of transcript levels based on the relationship between the genome and the cellular components. Objectivity is achieved by representing the biochemical processes in a cell in terms of thermodynamics, adopting a similar approach to other bottom-up research on a part of transcriptional control (6–11). The model sees the level of a transcript as a balance between velocities of synthesis and degradation, both of which are controlled by interactions between nucleotide sequences and protein factors, which are known to affect the levels of transcripts (12–14). The objectivity of the model allows it to be verified as an appropriate framework for analysis through comparison of derivable hypotheses with experimental results.

MODEL OVERVIEW

The basis of the proposed model is the existence of a quasi-equilibrium between the synthesis and degradation of each transcript. A cell forms a closed system for mRNA; transcripts will not go out from or come into the cell. This means that concentration of a transcript accumulated in a cell is determined by the velocity of synthesis and the velocity of degradation within the cell. It has been shown that each transcript has a unique half-life, i.e. the velocity of degradation is linear with respect to the concentration of the transcript (12). Consequently, the pseudo-equilibrium can be applied (6), and state of the equilibrium determines the level of the transcript. Although the half-life and velocity of synthesis can change frequently within each cell, giving rise to transient departures from this pseudo-equilibrium estimation, these deviations are not expected to be large and will rapidly attenuate in accordance with the half-life of the mRNA. This pseudo-equilibrium approximately describes the balance between the velocity of transcription (v_s) and the velocity of degradation (v_d) for a particular gene g, as follows.

$$v_{{\text{s}}_g}=-v_{{\text{d}}_g}.$$ 1

Although synthesis and degradation both involve multiple biochemical reactions, the velocities are determined by the slowest reaction as the rate-limiting step, as discussed below.

Regulation of mRNA synthesis

The rate-limiting step for mRNA synthesis is likely to occur at the onset of RNA elongation. For elongation to begin, the RNA polymerase II bound at the promoter must be hyperphosphorylated (15). Each phosphorylation step is energy-dependent, and should thus be restricted. This step cannot occur in parallel in the cell, and is unique to each gene. The velocity at this step can be described by considering a rapid pre-equilibrium between the binding and dissociation of RNA polymerase II with the promoter:

$${\text{promoter}}_g+\text{polymerase}{\displaystyle \underset{\text{fast}}{\overset{\text{fast}}{\leftrightarrows }}}{\text{complex}}_g{\displaystyle \stackrel{\text{slow}}{⟶}}{\text{transcription}}_g.$$ 2

At a certain frequency, the bound polymerase obtains the potential energy required to overcome the energy barrier, and then initiates transcription. Consequently, v_s can be described as a mathematical expectation determined by the concentration of the promoter–polymerase complex ([complex]) and the frequency (height of the barrier in Figure 1), as given by

$$v_{{\text{s}}_g}=k_{{\text{s}}_g}\left[{\text{complex}}_g\right],$$ 3

where k_s is a coefficient describing the frequency at which the polymerase enters the elongation state.

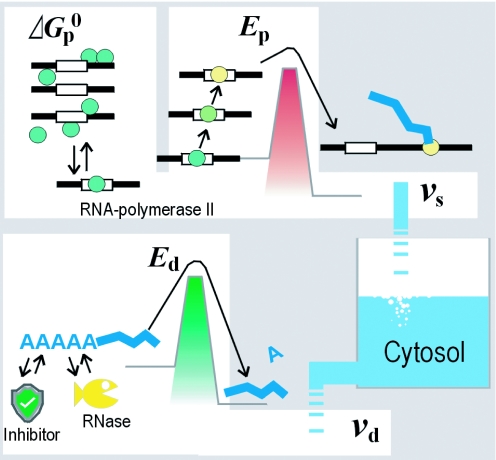
Figure 1.

Schematic representation of the proposed thermodynamic model. The accumulated amount of each transcript is in pseudo-equilibrium between influx and efflux. The velocity of synthesis for a transcript (v_s) is determined according to the Gibbs free energy $\Delta G_{\text{p}}^0$ (for equilibrium between binding and dissociation of RNA polymerase II to the promoter) and activation energy E_p (energy barrier for the start of polymerase elongation). The velocity of degradation (v_d) is determined by E_d (required to start hydrolysis). All energies are determined for interactions between special nucleotide sequences and the protein factors.

The concentration of the promoter–polymerase complex can be expressed as an equilibrium constant (K_p), as follows.

$$\begin{array}{c}{K}_{{\text{p}}_g}=\frac{\left[{\text{complex}}_g\right]}{\left[{\text{promoter}}_g\right]\left[\text{polymerase}\right]}\\ =\frac{{[\text{complex}}_g]}{(a_g{P}_0-[{\text{complex}}_g\left]\right)\left[\text{polymerase}\right]}.\end{array}$$ 4

Here, [promoter] is the concentration of the polymerase-free promoter; a_g is the local activity of the genome, the local activity represents the state of chromatin packing by histones at the promoter, and takes values between zero and unity. P₀ is the total concentration of the promoter. Solving Equation 4 leads to the concentration of the polymerase bound at the promoter ([complex]):

$$\left[{\text{complex}}_g\right]=\frac{a_g{P}_0{K}_{{\text{p}}_g}\left[\text{polymerase}\right]}{1+K_{{\text{p}}_g}\left[\text{polymerase}\right]}\approx a_g{P}_0{K}_{{\text{p}}_g}\left[\text{polymerase}\right].$$ 5

This approximation is based on the assumption

$$0<K_{{\text{p}}_g}\left[\text{polymerase}\right]=\frac{\left[{\text{complex}}_g\right]}{\left[{\text{promoter}}_g\right]}\ll 1.$$ 6

This pre-equilibrium condition thus tends to favor the dissociated state. This assumption is introduced to allow the state of pre-equilibrium to determine the velocity in Equation 3; only under this condition, the pre-equilibrium can define the frequency or length of time of complex formation, during which the polymerase is susceptible to the synthesis initiation (Figure 1).

The equilibrium constant K_p is determined by regulators, which are protein factors that bind around the promoter in a sequence-specific manner. Each of the regulators contacts the polymerase, affecting the equilibrium constant with a certain Gibbs free energy ($\Delta \Delta G_{\text{p}}^0$). The equilibrium constant is determined by the composite of the free energy as follows:

$$K_{{\text{p}}_g}=exp\left(\frac{-\Delta G_{{\text{p}}_g}^0}{RT}\right)=\text{exp}(\frac{{\sum }_{i=1}^n-\Delta \Delta G_{{\text{p}}_{i,g}}^0}{RT}).$$ 7

Here, R is the gas constant and T is the absolute temperature. The Gibbs free energy can be further described in terms of regulators, which are in equilibrium between binding and dissociation with particular cis elements. Using the activity concentration of free regulators ([regulator]), the Gibbs free energy can thus be rewritten as

$$\Delta G_{{\text{p}}_g}^0\equiv {\displaystyle \sum _{i=1}^n}\Delta \Delta G_{{\text{p}}_{ig}}^0={\displaystyle \sum _{i=1}^n}{a}_g{P}_0{K}_{{\text{c}}_{i,g}}{k}_{{\text{r}}_{i,g}}\left[{\text{regulator}}_i\right],$$ 8

where K_c is an equilibrium constant and k_r is an activity constant. The constant K_c indicates the affinity of each regulator for the cis element, and is determined by the nucleotide sequence. The constant k_r, however, indicates the function of each regulator to the gene, and is determined by the structure of the regulator and its spatial relationship with the polymerase. The nucleotide sequence around the promoter directs both of the determinants of k_r by selecting the regulator and fixing the position at binding. For genes hosting multiple binding sites for a regulator, the sum of K_ck_r values for all the binding sites represents a functional value for the combination of the regulator and the gene.

The frequency with which a bound polymerase enters the elongation state is affected by the stimulation of the mediator complex by enhancer-binding regulators (Figure 1). The complex phosphorylates the polymerase, changing the charge of the enzyme (15), which has been prevented from elongation by Coulombic force (13,14). The reduction of Coulombic force lowers the Arrhenius activation energy (E_p) for the initiation of elongation. According to the Arrhenius equation, the parameter k_s in Equation 3 can be represented by the composition of activation energies related to enhancer binding protein factors, as given by

$$k_{{\text{s}}_g}=A_{\text{p}}exp(\frac{-E_{{\text{p}}_g}}{RT})=A_{\text{p}}exp\left(\frac{-{\sum }_{l=0}^s\Delta E_{{\text{p}}_l}}{RT}\right),$$ 9

where A_p is a constant specific to the polymerase. Using a similar estimation for the function of promoter-binding regulator proteins, the activation energy can be described as

$$E_{{\text{p}}_g}\equiv {\displaystyle \sum _{l=0}^s}\Delta E_{{\text{p}}_{l,g}}={\displaystyle \sum _{l=0}^s}{a}_g{P}_0{K}_{{\text{e}}_{l,g}}{k}_{{\text{m}}_{l,g}}\left[{\text{Eregulator}}_l\right],$$ 10

where K_e is the equilibrium constant, k_m is an activity constant and [Eregulator] is the concentration of each free enhancer-binding regulator. The functions of the activity and equilibrium constants and the treatment for multiple binding sites are the same as in Equation 8. Equations 3, 5, 7 and 9 can finally be solved for the transcription velocity of the gene (v_s) as follows:

$$v_{{\text{s}}_g}=A_{\text{p}}{a}_g{P}_0\left[\text{polymerase}\right]\text{exp}\left\{\frac{-E_{{\text{p}}_g}-\Delta G_{{\text{p}}_g}^0}{RT}\right\}.$$ 11

Regulation of mRNA degradation

The rate limiting for degradation is probable to occur in the shortening or removal of the poly(A) tail (Figure 1). This slow step is immediately followed by decapping and then rapid removal of nucleotides from both termini. This sequential process is considered to be a common mechanism of degradation for properly synthesized mRNAs. The slow step is catalyzed by motif-specific nucleases, i.e. poly(A)-specific exonucleases and site-specific endonucleases. Inhibitor proteins that bind the same motifs, competing with the RNases, are also known. Each transcript may have a motif that determines the transcript's stability (12,16).

The velocity of degradation is thus considered to be proportional to the concentration of the transcript of the gene ([mRNA_g]), as given by

$$v_{{\text{d}}_g}=-k_{{\text{d}}_g}\left[{\text{mRNA}}_g\right],$$ 12

where k_d is a velocity constant determined by protein factors bound to the transcript in a motif-specific manner. As an enzyme or an inhibitor of an enzyme, an RNA-binding factor affects the activation energy of RNA hydrolysis (E_d) in the Arrhenius equation. The constant k_d in Equation 12 can be described in terms of this energy as

$$k_{{\text{d}}_g}=A_{\text{d}}\text{exp}\left(\frac{-E_{{\text{d}}_g}}{RT}\right),$$ 13

where A_d is a constant specific to RNA hydrolysis. Considering a rapid equilibrium between the binding and dissociation of RNA-binding proteins to the determinant motif of the mRNA, the composite of the activation energy is determined as

$$E_{{\text{d}}_g}={\displaystyle \sum _{j=0}^m}{k}_{{\text{h}}_{j,g}}{K}_{{\text{b}}_{j,g}}\left[{\text{RNA-bindingprotein}}_j\right],$$ 14

where k_h is an activity constant, K_b is an equilibrium constant and [RNA-binding protein] represents the activity concentration of each factor.

Accumulated amount of each transcript

Equations 1 and 11–13 lead to the following relationship between the energy parameters and the concentration of the transcript:

$$\left[{\text{mRNA}}_g\right]=k_{\text{c}}{a}_{g}exp\left(\frac{-E_{{\text{p}}_g}-\Delta G_{{\text{p}}_g}^0+E_{{\text{d}}_g}}{RT}\right).$$ 15

Here, k_c is a constant specific to a cell and is given by k_c = A_pP₀[polymerase]/A_d. The parameters $\Delta G_{\text{p}}^0$, E_p and E_d are determined by the activity concentrations of the protein factors bound to specific nucleotide sequences of DNA or RNA as described in Equations 8, 10 and 14, respectively.

HYPOTHESES AND VERIFICATION

Lognormality in data distribution

For verification of the proposed model, a number of hypotheses derived from the model were tested against the relevant characteristics of measured transcriptome data. The first feature of transcriptome data considered is the statistical distribution of concentrations of transcripts in a cell. The model predicts that the protein factors (Equations 8, 10 and 14) will be basically independent of other factors, while the distributions of these factors with respect to $\Delta \Delta G_{\text{p}}^0$, ΔE_p and ΔE_d will have common characteristics owing to the commonality of the physical bases. The composites of the energies can thus be considered to be the sums of independent, identically distributed variables. According to the central limit theorem, the distribution of ($-\Delta G_{\text{p}}^0-E_{\text{p}}+E_{\text{d}}$) in Equation 15 will be normal, leading to a lognormal distribution of [mRNA_g].

This hypothesis can be verified by comparison with comprehensive transcriptome data. Expressional microarray data for any organism on any analytical platform follows a three-parameter lognormal distribution (17), with an additional third parameter for compensation of signal background. This three-parameter distribution has been observed repeatedly in hundreds of experimental datasets on different platforms, providing strong support for this model-derived hypothesis.

Stability in scale parameter

The model also predicts a stable characteristic for the scale parameter of the log[mRNA_g] distribution. According to Equation 15, the scale parameter is defined by the distributions of energetic parameters. These distributions would be stable and common because all can be considered to represent the sums of variables. Changes in the parameters therefore indicate a total shift in protein–nucleic acid interactions, and such shifts will require changes in the conditions of the cell, such as salt content or pH. However, the conditions of the cell will remain stable owing to the homeostatic character of cells in general. The stability of the scale parameter has been observed experimentally (17), supporting this prediction. The stability and mode of distribution are checked routinely in experiments as part of the microarray normalization process.

Multiplicative effects to [mRNA]

Another hypothesis derivable from the proposed model is the multiplicative change in transcript concentration by each protein factor. According to Equations 8, 10, 14 and 15, additive changes in the activity concentrations of the factors will cause additive changes in energy, which will in turn cause multiplicative changes in [mRNA]. Generally, a stimulus applied to a cell induces a change in the activity concentrations of certain protein factors, which in turn affects the concentrations of certain transcripts. These effects can be measured by conducting paired microarray experiments in which the changes are measured as ratios (17). If the hypothesis is correct, the ratios resulting from the application of a pair of simultaneous stimuli will coincide with the products of the ratios provoked by each individual stimulus. Such combinations of measurements have been reported in a series of experiments on the effects of environmental changes in yeast (18). In these experiments, a linear relationship was obtained for numerous combinations of stimuli following the products of the individual ratios (Figure 2A). It should be noted that the slight overestimation of the product can be attributed to the effect of medium replacement (18), which is counted twice in the product calculations. This correlation could not have been obtained by chance or systematic error, since the replacement of any of the ratios in a combination with another in a different time phase (i.e. a different stage of response) almost eliminates the relationship (Figure 2B). Thus, the multiplicative effect of factors predicted by the present model is supported by experimental findings.

Figure 2.

Multiplicative effect of factors confirmed in microarray experiment. (A) Scatter plots comparing measured transcriptome changes with estimated changes. Measurements were taken 30 min after the simultaneous application of heat shock and osmotic shock (18). The estimated change was calculated by multiplying the measurements for each type of shock. (B) Reference plot with one of the datasets replaced with another in a different time phase. (Calculated data as well as parameters and raw data are provided in Supplementary Data sheet.)

DISCUSSION

The proposed model describes transcriptome formation in a cell on the basis of thermodynamic expressions. The model is expected to provide both the fidelity of a bottom-up approach and the objectivity required for evaluating its appropriateness. The observed characteristics of transcriptome data support the model. Although the verifications presented above are somewhat indirect, the objectivity of the proposed model should allow many other types of verification using transcriptome analyses.

The model can be used to identify the quantitative aspects of genome information giving the transcriptome. The genome is presented by the model in terms of two series of constants (equilibrium and activity constants) as a decoded form of the quantitative information. The constants in a genome locus can be determined through in vitro kinetic experiments. With accumulation of such measured data, it will become possible to predict the values by simulations in silico.

The nucleotide sequences do not encode all of the information necessary to reproduce the chromatin structure or factor activity concentrations, giving rise to the observed variety among transcriptomes. The structure is controlled by chemical modifications of histones (19), which are directed by covalent modification of the DNA. Tight restrictions on the changes in the nucleosome effectively preserve the modifications of histones at the locus when the genome is replicated (20). Alterations of DNA may instead be introduced during the development of multicellular organisms (21). Accordingly, such modifications seem to play an important role in cell differentiation, causing static changes in the transcriptome. Thus, the value of a_g is expected to be relatively stable.

This model provides objectivity for transcriptome data analyses. For example, the synergy of additive effects, as commonly observed in combinations of stimuli or the artificial induction of factors (9,10), can be assessed in a more objective manner by the proposed model as the product of effects (Figure 2a). This shows that the protein factors that had changed the expression levels within the short time course experiment practically worked independent to each other. The independence supports the assumption that the pre-equilibrium condition of many protein factors tends to favor the dissociated state; any two factors that have neighboring or overlapping binding sites rarely interfere with each other, since chances that the factors hit with each others at the site are rather small. Of course, this observation obtained by a transcriptome analysis of yeast does not deny existence of dependences, which includes interference or stabilizing, between factors. For example, some constitutive factors may tend to favor to the binding state; such constitutive factors can bind to certain sites and affect other factors' binding for a long period, producing a tendency of the corresponding genes' expression levels. However, a constitutive factor would influence only limited genes and factors, since it can affect to molecules that are reachable at its binding state. Additionally, if dependences are common to factors' effects, they might cause contradict to the required condition of the central limit theorem, providing conflicts with the observed distribution of transcriptome data.

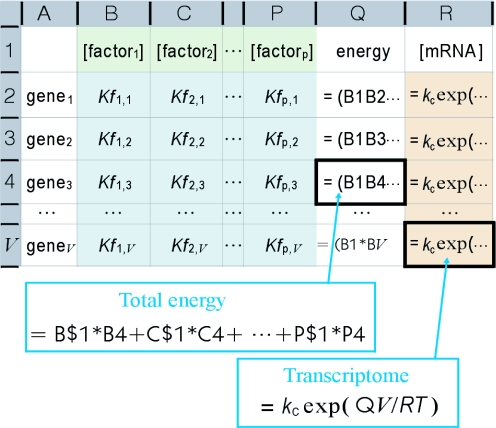
The transcriptome is represented in the model as a series of functions of protein factor activity concentrations (Equations 8, 10, 14 and 15). Protein factors can be expected to be dispersed uniformly in the corresponding cellular compartments owing to the rapid diffusion typical of large soluble molecules (22). Consequently, the activity concentration of a protein factor is probable to common to the genes. Equation 15 can thus be generalized to any gene, providing a series of simultaneous equations consisting of all genes in a genome (each equation forms a row in the spreadsheet shown in Figure 3). The low concentrations and substantial variations of specific activities owing to chemical modifications render the activity concentrations difficult to measure at present. However, if the activity and equilibrium constants k and K and local activity a_g are available, the values can be derived from transcriptome data by solving the set of simultaneous equations. The set of activity concentrations can then be used to trace the changes in the transcriptome back to changes in each factor. The effect of changes in the factors can also be estimated by substituting activity concentration values, allowing the proper set of stimuli required to obtain the desired transcriptome to be predicted by simulation.

Figure 3.

Transcriptome estimation from genomic information. The matrix of coefficients (blue) indicates quantitative decoded genome information determined by interactions between genes and protein factors. The concentrations of transcripts (orange) are calculated from the activity concentrations for each of the protein factors (green). The transcriptome is determined from the values in column R. The activity concentrations in row 2 are determined by solving the simultaneous equations analytically with a partial set of column R values supplied by experimental microarray data.

METHODS

Estimation of simultaneous stimuli effect

Data for heat shock, hypo-osmotic shock and the simultaneous application of both stimuli (18) were calculated by a parametric method (17). The combined effect of the two stimuli was estimated from the individual effects (measured in experiments 7547 and 2555) by multiplying the obtained ratios. The logarithms of the estimated ratios were plotted against the log ratios for experimental data (experiment 4787; Figure 2A). For comparison, data from experiment 4787 was exchanged with that for experiment 4786, representing data for a different time point in an identical experiment (Figure 2B). (Calculated data as well as parameters and raw data are provided in Supplementary Data sheet.)

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.