Taking the mystery out of biological networks

Fifty years ago, our grandparents considered it a luxury to make a long-distance telephone call or to travel by plane. Today, we can speak to and e-mail each other instantly, and meet face-to-face in a matter of hours despite the intercontinental distances that often separate us. The smooth functioning of this new technological world relies heavily on the complex sets of connections between its parts. Microchips contain an array of components that are linked to each other to build computers, which are then connected through the Internet. Interconnected, cross-referenced and hyperlinked: we live in a networked world.

Complex systems are often networked and biology is no exception. The follow-up experiments to the genome sequencing projects, such as those using microarrays or the yeast two-hybrid system, show that molecules in living organisms are also highly connected. This interconnectivity helps to explain how such great complexity can be achieved by a comparatively small set of molecules either in a single organism or in nature as a whole.

Most real-world networks, including those based on social acquaintances, the World Wide Web and those that are revealed by biological data, share certain intrinsic properties that are described as 'scale-free' behaviour (Barabasi & Albert, 1999). First, the distribution of the number of connections per node (that is, an element in the network) follows a power law: most nodes have few connections with an increasingly small number of 'hubs' being highly connected. Indeed, most personal home pages are linked to the hub 'Google', but they do not usually connect to each other. Second, they are 'selfsimilar': any part of the network is statistically similar to any other. For example, the British Airways and Lufthansa route networks appear to be similar in structure despite having different nodes and hubs (London Heathrow and Frankfurt, respectively). These networks also show 'small-world' behaviour: any two nodes can be connected through a small number of intermediates (also termed 'small diameter'), and when two nodes are connected to a third they also tend to be connected themselves ('highly clustered'). The idea that most people in the world are connected by acquaintance through fewer than six other people is perhaps the best-known example of this phenomenon. Third, and finally, networks are highly tolerant to random failures: a significant fraction of the nodes can be removed without affecting overall behaviour, but they are highly vulnerable to attacks aimed at the hubs. The loss of most personal computers would scarcely affect the Internet, but the loss of one of the 26 key servers in the world that are responsible for redirecting requests would be a catastrophe.

These common network properties help to explain several features of biological systems, such as the extraordinary ability of yeast to tolerate single-gene deletions. This resilience cannot be entirely attributed to redundancy (through multiple copies of a gene), and it has been suggested that the lethality of a deletion is highly correlated to the gene centrality or to the number of connections that it has (Albert et al, 2000). If you remove the cell equivalent of an Internet service provider, you usually kill the organism.

However, it is important not to push these comparisons too far, particularly as biological networks are sometimes more abstract than their physical world counterparts and are often just a handy way of representing complex data. For instance, the Internet consists of highly similar nodes with static relationships that correlate reasonably well with geography, whereas protein-interaction maps are averaged over many different cellular conditions, lack information about concentration and typically contain errors.

A mystery that is the subject of some debate is why networks that are derived from completely different data sources have such similar properties. For biological networks, several arguments have been put forward. One compelling explanation is that duplication of large parts of the genome (Wagner, 1994; Papp et al, 2003) would lead to large subnetworks being duplicated, and that this would easily lead to the scale-free, small-world behaviour observed. Alternatively, it has been argued that there might be selective pressure acting on the topology of the network: some network structures might be more advantageous to the organism than others (Guelzim et al, 2002; Wuchty et al, 2003). However, no strong evidence had been presented to support these, or indeed any other, hypotheses. Two timely papers in EMBO reports have now provided just that (Amoutzias et al, 2004; van Noort et al, 2004). The results are surprising and both papers, despite differences in approach, reassuringly agree.

Amoutzias and colleagues combine phylogenetic, proteomic and structural information to study the evolution of the gene-regulatory network of basic helix–loop–helix (bHLH) transcription factors (Amoutzias et al, 2004). This is an ancient family of transcription factors in higher eukaryotes, which form either homo- or heterodimers and subsequently activate or suppress the expression of a range of genes. Here, the scale-free, small-world network consists of single transcription factors that are connected if they are able to dimerize. The authors found that single-gene duplication and domain-rearrangement events could explain the emergence of gene networks with almost identical topology. They also noted that the similarities between different parts of the network are likely to be the result of convergence, because phylogenies do not support largescale gene duplications.

In another paper, van Noort and colleagues investigate the topology of gene co-expression networks in yeast (van Noort et al, 2004). Here, the scale-free, small-world network consists of genes that are connected when they are expressed under similar cell conditions. They also note a correlation between the fraction of co-expressed paralogues (that is, homologous genes in the same organism) and their sequence identity. Previous models for network evolution (Barabasi & Albert 1999; Ravasz et al, 2002) can account neither for combined scale-free and small-world characteristics nor for the correlation between co-expression and sequence similarity. In this paper, the authors suggest a simple model based on the co-duplication of genes and their transcription-factor binding sites: deletion and duplication of these binding sites together with gene loss can explain both findings.

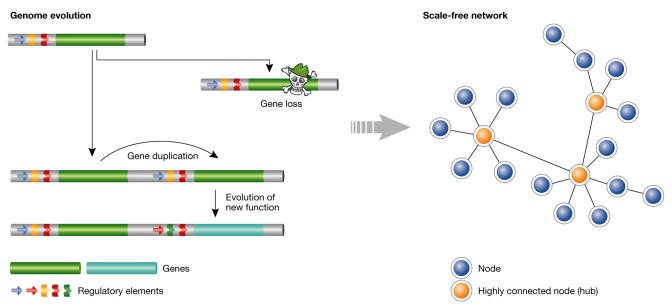
The unifying theme of the two papers is that scale-free, small-world behaviour can, in principle, arise simply from the types of genetic evolutionary events to which we are most accustomed: gene duplication, point mutation and gene loss (Fig 1). Both findings argue against selective pressure on network topology, although they do not rule out this possibility, and both recommend caution when making biological interpretations of network architectures.

Figure 1.

Biological scale-free, small-world networks can arise spontaneously as a result of simple evolutionary events such as gene duplication, evolution of a new function and gene loss.

The study of networks is an important part of molecular biology today. Without it, we have little chance of making biological sense of much of the complex data that are now being generated. Parallels can, and certainly should, be made with networks in the rest of the world, and these will continue to reveal new insights. However, to be most useful, it is important to avoid analyses of the global characteristics of networks without careful study of their constituents. Most biological networks are incomplete and difficult to interpret owing to the peculiarities of the data and the experiments that generate them. Any models for their origin or behaviour will need to be carefully tested and constantly revised. And, it should always be remembered that biological networks are not necessarily as mysterious as they seem. As the two papers discussed here highlight, the simplest explanations might well be right under our noses.