Hormesis: a revolution in toxicology, risk assessment and medicine

Summary

Re-framing the dose–response relationship

Anyone applying for life insurance knows he or she faces an interview. The insurance agent will inquire about age, family history of diseases, health problems and medical history, smoking behaviour, occupation, lifestyle and many other details. These data are then fed into sophisticated mathematical models to calculate premiums and royalties based on the personal health risks of the individual. With the financial stakes high for both the insurer and the insured, this creates a level playing field based on realistic expectations that is essential for the mutual benefit of both parties. Similar to life insurers, many financial, pharmaceutical and other businesses use such risk-analysis-based realistic data to calculate the possibilities of risk or harm in contrast to benefits and/or costs.

The main challenge facing environmental risk assessment is the extrapolation of data

In striking contrast to risk modelling based on gathering as much useful real-world data as possible, the field of environmental risk assessment, which governs the quality of community air and water, the safety of food and the clean-up of contaminated sites, has been based principally on unverifiable assumptions and speculations. The main challenge facing environmental risk assessment is the extrapolation of data. Regulators must extrapolate results not only from animal toxicity studies, typically from mice and/or rats to humans, but also from the very high doses usually used in animal experiments to the very low doses that are characteristic of human exposure. These two types of extrapolation are steeped in uncertainty. The failure of regulatory agencies during the past three decades, when risk assessment was first applied to environmental regulations, to resolve in reasonable measure these uncertainties has led to a protectionist public health philosophy in which conservative assumptions became accepted at each point in the risk assessment process. The cascade of risks resulting from such a protectionist stance has resulted in increasingly stringent environmental standards whose benefits and risks cannot be adequately measured but whose costs are often extraordinarily high. It is this decoupling of the potential risks from the financial cost needed to avoid those risks that sets the field of environmental risk assessment apart from the rest of the healthcare world. And although the costs for industry and the public keep growing, there is little evidence or hope of progress despite numerous published texts and journals and the many thousands of professionals engaged in detailed study and evaluation.

It is [the] decoupling of the potential risks from the financial cost needed to avoid those risks that sets the field of environmental risk assessment apart from the rest of the healthcare world

...our cells have developed mechanisms to detoxify harmful chemicals and exposure to radiation—in fact, low doses may even trigger responses that are beneficial

The extrapolation from high to low doses, as performed by nearly all regulatory agencies concerned with environmental risk assessment and as portrayed in leading toxicological texts, further depends on whether the compound of concern is a carcinogen or a non-carcinogen. For carcinogens, regulatory agencies now take the stance that risk is directly proportional to exposure in the low-dose zone and that, consequently, there is no safe level of exposure. This so-called linear non-threshold (LNT; Fig 1) dose–response model has become the standard model for assessing the health risks of chemical carcinogens and radiation by regulatory agencies in many countries. As for non-carcinogens, the same regulatory agencies assume that there is a threshold dose, below which there is no risk of harm.

Figure 1.

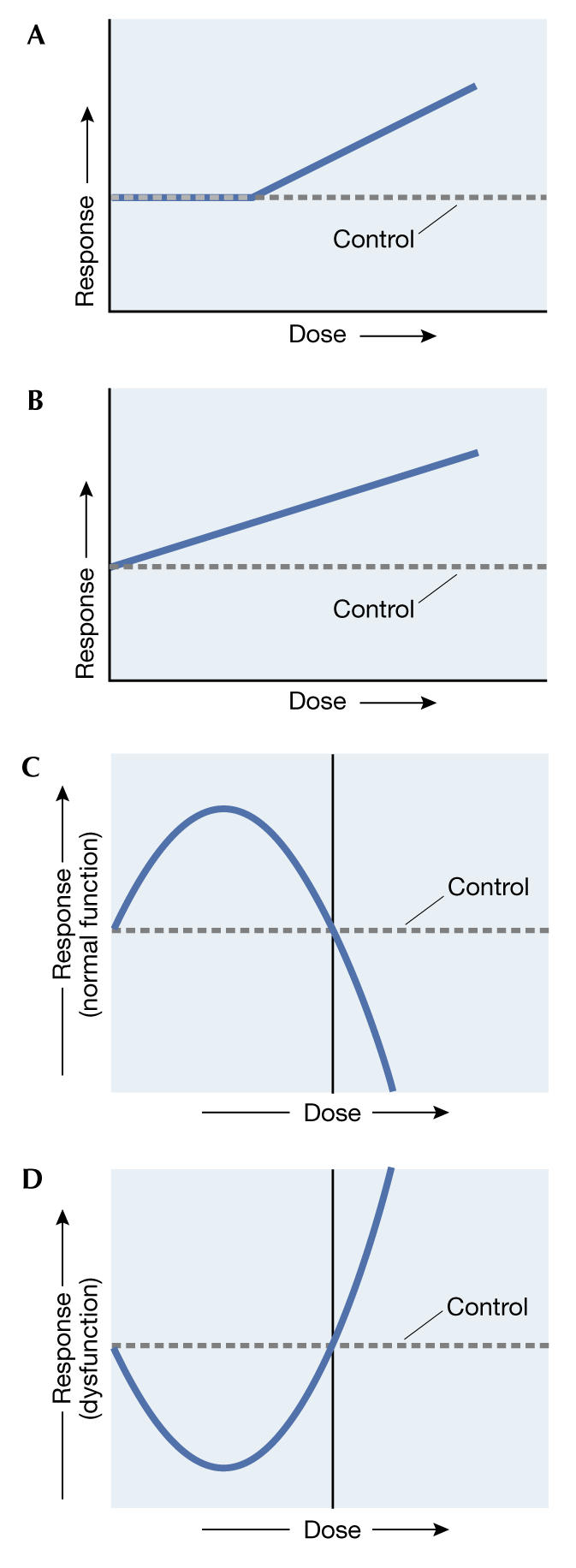
Dose–response relationships described by (A) the threshold model, (B) the linear non-threshold model, (C) the inverted U-shaped hormetic model and (D) the J-shaped hormetic model. (Adapted from Davis & Svendsgaard, 1990.)

The practical consequences of the LNT model have been quite problematic. Regulatory agencies have often defined very low acceptable risks and accordingly set very low permissible exposures when dealing with carcinogens. But these exposures are usually far from the experimental data. A typical risk assessment of one additional case of cancer per million people over a 70-year lifetime can require an extrapolation more than 5–6 orders of magnitude from the high exposures used in animal studies to the low concentrations assumed to be safe for humans. In reality, this means that although lifetime bioassays expose a rodent to hundreds of milligrams per unit of body weight per day, the permitted exposure to humans may be fractions of a microgram per unit of body weight per day. This is an extraordinary degree of extrapolation with the uncertainty increasing progressively the further the prediction moves away from the observable zone of generated data. Furthermore, the assumption of a linear relationship between dose and response completely ignores the fact that our bodies and our cells have developed mechanisms to detoxify harmful chemicals and exposure to radiation—in fact, low doses may even trigger responses that are beneficial.

In addition, risk predictions based on the extrapolation of data from animal experiments using high doses are in fact hard to verify, despite massive attempts that used up to 24,000 rodents in the largest of all—failed—validation experiments. Even such powerful studies, which were carried out in an acceptable manner and evaluated in extraordinary detail, cannot reliably estimate risks lower than one in 100, let alone one in 1,000,000. But because risks of one in 100 are regarded as being unacceptable to the general public, especially for routine activities, regulatory agencies have found themselves in a position where they have had to adopt the use of the lowest estimated risk, which cannot be checked or verified. This approach clearly is marked by good intentions but paved with a large public cheque book.

Despite a lot of argument between governmental agencies and the affected industries over the process of risk assessment, industry has made little progress in persuading governmental agencies to budge from their protectionist stance, especially in the areas of hazard assessment and its impact on risk assessment. In general, it has been nearly impossible for biostatistical models to differentiate between linear and threshold models in the low-dose zone when experimental studies used only 2–4 different doses. In such cases, the governmental regulatory agencies usually revert to their more conservative default assumption models.

If only zero risk is acceptable to the public, then it is easy to call for the complete abolishment of a product or activity that carries with it some risk, no matter how large the costs or benefits

Nevertheless, the threshold dose response has become the key model in toxicology and pharmacology, whereas the LNT dose–response model has been the principal model for the estimation of cancer risks by virtually all regulatory agencies. I would argue that the field of toxicology, including most regulatory agencies concerned with chemical and radiation risk, has made a major error of judgement in selecting these two dose–response models to calculate human health and environmental risks for the broad spectrum of chemical classes and physical agents. This error profoundly affects the standards set for public health, the communication of risks to the public, the establishment of environmental priorities and the costs of environmental standards and clean-up activities. It has also made the decision-making process more intuitive and less scientific and thus more susceptible to political manipulation by interested parties. If only zero risk is acceptable to the public, then it is easy to call for the complete abolishment of a product or activity that carries with it some risk, no matter how large the costs or benefits.

...the hormesis model clearly outperforms either of the other two competitive models in fair head-to-head competition

Enter an alternative model, which claims that the fundamental shape of the dose–response curve is neither linear nor threshold, but rather U-shaped. This so-called hormesis model—after the Greek word 'to excite'—was first applied to describe dose–response relationships by Southam & Ehrlich (1943) more than 60 years ago. A typical hormetic curve is either Ushaped or has an inverted U-shaped dose–response, depending on the endpoint measured. If the endpoint is growth or longevity, the dose–response would be that of an inverted U-shape; if the endpoint is disease incidence, then the dose–response would be described as U- or J-shaped (Fig 1). This model not only challenges the LNT and threshold models but, more importantly, it suggests that as the dose decreases there are not only quantitative changes in the response measured but also qualitative changes. That is, as the dose of a carcinogen decreases, it reaches a point where the agent actually may reduce the risk of cancer below that of the control group.

Of course, a protectionist philosophy dominated by a linear dose–response model and obsessed with achieving zero risk will have difficulties accepting this notion. During the past decade we have therefore made a concerted effort to determine whether the concept of hormesis is real and generalizable, as well as toxicologically and biologically significant. To this end, we have developed a rigorous a priori process to assess and quantitatively evaluate possible hormetic dose–response relationships, estimate the frequency of hormetic dose responses in the toxicological literature and estimate which toxicological model occurred more frequently in the peer-reviewed literature (Calabrese, 2002, 2003; Calabrese & Baldwin, 2001a, 2003b). Our activities have shown that hormetic dose responses are more common than the traditional toxicological threshold model, can be generalized well by model, endpoint and chemical class, and display a predicable set of quantitative dose–response features in terms of magnitude and width of the stimulatory response. In short, the hormesis model clearly outperforms either of the other two competitive models in fair head-to-head competition (Calabrese & Baldwin, 2001b, 2003a).

But despite the obvious superiority of the hormetic model over the linear model at low dose and the threshold model, toxicological thinking has so far been hesitant to accept and apply it. The reasons for this reluctance to change are complex but can be traced in large part to the fact that toxicology has been, primarily, an applied discipline with the laudable goal of protecting health. Faced with a huge number of compounds to be tested, toxicologists therefore streamlined their processes to reduce the number of animals used per dose and the number of doses per experiment. A typical toxicological examination derives study-specific LOAELs (lowest observed adverse effect levels) and NOAELs (no observed adverse effect levels) from experimental data using animal models in which only 2–4 different doses of the compound under scrutiny are used—plus control groups, of course. With the goal of deriving a NOAEL with the fewest doses possible, it becomes immediately obvious that any insights into what is happening in the domain below the NOAEL cannot be obtained by such studies. Furthermore, it takes many more doses—and, accordingly, animals and time—to get a clear picture of the domain in which hormesis takes place.

It is important to recognize that the dose–response relationship is the most important aspect in toxicology, around which all research and teaching is centred. It is therefore both troubling and of great concern that this field could have accepted a flawed toxicological dose–response model but also built an entire educational and regulatory edifice on it with serious repercussions for academia, industry and the public. A detailed re-examination of this historical blind spot in toxicology reveals a complicated web of interacting factors that led to the demise of the hormesis hypothesis: first and foremost the principal concern with high-dose effects, limited study designs and difficulties in assessing the typically modest hormetic responses especially within the framework of weak study designs. The field also saw bitter historical rivalries between traditional and homeopathic medicine, the latter regarding hormesis—that is, the Arndt–Schulz Law—as a central explanatory feature. This has resulted in a lack of intellectual leadership by those supporting a 'hormetic' perspective and a lack of governmental funding of the hormesis concept during the formative years of toxicological development from the 1930s onwards (Calabrese & Baldwin, 2000a–e). All these factors contributed to today's situation, in which hormesis, despite growing supportive evidence mainly from biomedical research, has only a spotty and peripheral role in toxicology.

But, if accepted, the hormetic dose–response model could have a large impact on risk assessment in many significant ways. It would not even require a complete rethinking in toxicology as the hormetic response is a normal component of the traditional dose–response relationship. And because hormetic dose responses are similar for carcinogenic and non-carcinogenic agents, it has the potential to harmonize risk assessment procedures for carcinogens and non-carcinogens alike, which have so far been treated differently.

But what is particularly important is the fact that the hormetic dose response occurs in the observable zone of the experimental data. This means that we would not need to extrapolate experimental data far into the realm of the uncertain as is done at present in cancer risk assessment, which relies on the animal-derived LNT predictions. Thus, we could replace this scientifically questionable practice with a verifiable procedure. In fact, as the hormesis hypothesis can actually be tested with the available data, for the first time in the modern history of cancer risk assessment, we would be able to rely on a verifiable dose–response model and not depend on unverifiable extrapolations of animal data to estimate actual risk to humans.

The most fundamental change in the risk assessment process would be the adoption of the hormetic model as the default risk assessment tool to replace the outdated LNT model for carcinogens and the threshold model for non-carcinogens. Because the number of dosages used in most bioassays, especially those used by governmental agencies such as the US National Toxicology Program, is modest (3–4 dosages), there is little likelihood that the respective models sufficiently differ from each other in their predictive power. Thus, regardless of which dose–response model is selected as the default, it will be used in most cases. Typically, the selection of a default model has been driven by a concern of the regulatory agencies to err on the side of safety, given all the uncertainties associated with extrapolating over many magnitudes. In addition to being guided by a protectionist public health philosophy, the selection of a default model also assumes objective superiority over its competitors—both theoretically and based on experimental or empirical data. Substantial evidence now exists to support the scientific advantage of the hormetic model over its competitors. Given this situation, it would seem that the time has come to re-examine which model should be selected as the default in environmental risk assessment.

Perhaps the most exciting aspect of adopting the hormetic hypothesis in environmental risk assessment is that it would allow the field to move forward scientifically. It would replace the present status of compelling society by acting on the basis of assumptions that cannot be adequately tested by a new risk assessment procedure that can be realistically evaluated with its results displayed visibly in the observable zone. This would be a major first step in placing 'modern' environmental risk assessment on a similar level with other types of 'health insurance', where risk estimates are based on data that do not require extraordinary extrapolations and where the findings create a heightened sense of confidence.

The dose–response relationships for medical agents commonly display the same hormetic dose–response relationships as their toxic counterparts

But despite the obvious superiority of the hormetic model over the linear model at low dose and the threshold model, toxicological thinking has so far been hesitant to accept and apply it

The concept of hormesis also has important implications for the field of clinical medicine. The dose–response relationships for medical agents commonly display the same hormetic dose–response relationships as their toxic counterparts. Many agents, such as antibacterials, antifungals, antivirals and tumour-fighting drugs, display hormetic dose responses. The clinical significance of this has only recently begun to dawn on the medical community, although it was recognized as early as the mid-1940s for antibiotics such as streptomycin. The consequences for human health are quite serious. As the concentration of a drug in the human body decreases over time, the agent against which the drug is targeted could enter a growth-stimulating zone, a condition that could be good for the microbe or a tumour but bad for the patient. In addition, hormetic dose–response curves are observed in other medical settings: the selection of dosages for drugs to enhance cognitive function, grow hair, enhance immune function and numerous other bodily activities. A broader recognition of the hormetic dose response in the wider biomedical domain has the potential to usher in a vast array of new opportunities for understanding basic biological processes and to exploit such knowledge in the development of new products and the improved treatment of patients.