PKQuest: capillary permeability limitation and plasma protein binding – application to human inulin, dicloxacillin and ceftriaxone pharmacokinetics

Abstract

Background

It is generally assumed that the tissue exchange of antibiotics is flow limited (complete equilibration between the capillary and the tissue water). This assumption may not be valid if there is a large amount of plasma protein binding because the effective capillary permeability depends on the product of the intrinsic capillary permeability (PS) and the fraction of solute that is free in the blood (fw_B). PKQuest, a new generic physiologically based pharmacokinetic software routine (PBPK), provides a novel approach to modeling capillary permeability in which the only adjustable parameter is the PS of muscle.

Methods

All the results were obtained by applying PKQuest to previously published human pharmacokinetic data.

Results

The PKQuest analysis suggests that the highly protein bound antibiotics dicloxacillin and ceftriaxone have a significant capillary permeability limitation. The human muscle capillary PS of inulin, dicloxacillin and ceftriaxone was 0.6, 13 and 6 ml/min/100 gm, respectively. The ceftriaxone protein binding is non-linear, saturating at high plasma concentrations. The experimental ceftriaxone data over a wide range of intravenous inputs (0.15 to 3 gms) was well described by PKQuest. PKQuest is the first PBPK that includes both permeability limitation and non-linear binding.

Conclusions

Because of their high degree of plasma protein binding, dicloxacillin and ceftriaxone appear to have a diffusion limited exchange rate between the blood and tissue and are not flow limited as had been previously assumed. PKQuest and all the examples are freely available at http://http:\\www.pkquest.com.

Background

The goal of physiologically based pharmacokinetic models (PBPK) is to describe the whole body drug distribution and metabolism in terms of an accurate physiological model of the animal. The most difficult component to model is the description of the exchange between the blood and tissue. This is a complicated process, involving, e.g., transport across the capillary and tissue cell membranes and diffusion in the extravascular and cellular space. Because of this complexity, some simplifying assumptions must be made in order to incorporate it into a PBPK. PKQuest is a new general purpose PBPK software routine that has previously been used to model the human pharmacokinetics of propranolol [1], D₂O and ethanol [2], and the volatile solutes and anesthetics [3]. In PKQuest, this blood-tissue exchange for organ i is characterized by the parameter fclear [i] defined by (see [1] for details):

(1)     fclear [i] = (c_A - c_V)/(c_A - c_T)

where c_A, c_V and c_T are the free water concentrations in the artery entering the tissue, the vein leaving it, and the (assumed) well mixed tissue space, respectively. Fclear is a measure of the fraction of solute that equilibrates with the tissue in one pass through the capillary. In the limiting case where the capillary is impermeable, c_A = c_V and fclear = 0. At the opposite extreme, where exchange is very fast and the venous concentration equilibrates with the tissue, c_V = c_T and fclear = 1. This latter case is referred to as "flow-limited" because the blood-tissue exchange becomes limited by the blood flow. Flow limitation simplifies the PBPK because it eliminates the necessity of having to determine the value of fclear [i]. Because of this simplicity, the vast majority of PBPKs in the literature assume that the exchange is flow limited [4].

The parameter fclear [i] (eq. 1) of organ i can be related to the capillary permeability-surface area product (PS_i, liters/min/Kg) by the relation (see [1] for derivation):

where fw_B is the fraction free in the blood, F_i is the organ blood flow (liters/min/Kg), wfract_B is the fraction of water in the blood (liters/Kg) and ρ_B is the blood density. As the permeability PS becomes large, fclear approaches 1 (the flow-limited condition). It can be seen from eq. 2 that the value of fclear [i] depends on 3 different physiological PBPK parameters (PS_i, F_i, and fw_B). The design of PKQuest implements a unique feature that makes it easy for the user to test whether the solute under study has some significant capillary permeability limitation. PKQuest has preprogrammed the relative values of PS_i for organ i relative to the value of PS_muscle of the muscle capillaries based on previous experimental measurements (reviewed in Crone and Levitt, [5]). Thus, the capillary permeability for all the organs is determined by just one adjustable parameter, the fclear for muscle. PKQuest uses this value of fclear [muscle] to find PS_muscle from eq. 2, uses the stored ratios PS_i/PS_muscle to find the value of PS_i, and then uses eq. 2 to find the value of fclear [i] for all the other organs. In addition to simplifying the implementation of the capillary permeability limitation, this also has the major advantage that it ensures that the values of fclear [i] for the different organs are correctly adjusted for the organ blood flow (F_i) and fraction free in blood (fw_B) and have the appropriate PS value relative to muscle.

All previous PBPK analysis of antibiotics have assumed that the antibiotic was flow limited. It can be seen from eq.2 that the value of fclear is determined by the product of the intrinsic capillary permeability (PS) and the fraction of drug that is free in the blood water (fw_B). This implies that drugs that have a high degree of binding (small fw_B) are especially likely to have some capillary permeability limitation (i.e., not flow limited). The two antibiotics that are investigated in this paper (dicloxacillin and ceftriaxone) were chosen as likely candidates for having some permeability limitation because they have a high degree of protein binding (small fw_B) and they are both relatively lipid insoluble so that one would predict that they would not have high intrinsic PS values.

Ceftriaxone has the additional complication that the protein binding is non-linear, saturating at high concentrations. Incorporating non-linear binding greatly complicates the kinetic equations (see [1] for details) and for, this reason, is not included in most PBPKs. A notable exception is the investigation by Tsuji et. al. [6] of the kinetics of cefazolin in the rat, an antibiotic with non-liner protein binding. Although this PBPK analysis by Tsuji et. al. [6] is one the most complete and extensive in the literature, it was assumed that cefazolin was flow limited and did not include a permeability limitation. PKQuest is the first PBPK that allows for the combination of both non-linear binding and a permeability limitation. PKQuest has also reduced the number of parameters that must be entered to characterize the protein binding. The extravascular extracellular albumin concentration in the different organs (cProt [i]) relative to the albumin concentration in plasma (cProt [vein]) has been preprogrammed (these values are based primarily on the measurements of Tsuji et. al. [6] for the rat). Assuming that the protein binding in the different organs is proportional to the albumin concentration, the user needs to enter just the binding parameters for plasma and PKQuest will then automatically determine the corresponding binding parameters for all the organs.

The following sections will present a detailed description of the application of PKQuest to the human pharmacokinetics of dicloxacillin and ceftriaxone. For this analysis it is useful to establish a reference PS value for a solute that is known to be permeability limited. For this reason, PKQuest will first be used to determine the capillary permeability of inulin, a large water soluble molecule that is known to be capillary limited [5].

Methods

PBPK program and its assumptions

PKQuest [1] was used for all the analysis in this paper. The details of the implementation of the program and a complete derivation of the pharmacokinetic equations is described in [1]. It is assumed that each organ can be modeled as a single well-stirred compartment. This is clearly an approximation and effects such a diffusion gradients, countercurrent exchange and heterogeneous organ blood flows [7-9] will produce small deviations from this assumption.

The free water solute concentration (c, moles/liter) plays a central role in these calculations because the rate of exchange across the capillary depends on differences in the value of c between the capillary and tissue (see eq. 1). For the blood or any organ, the free concentration can be related to the total (measured) concentration (C_tot, moles/Kg) by the relation C_tot = c wfract/fw where wfract (liters/Kg) is the water fraction in the organ and fw is the fraction of the solute that is free in the water phase. The parameter fw_i, the fraction free in organ i (including vascular compartments), characterizes the fraction free (and bound) and the corresponding tissue/blood partition coefficients. Solute binding is a ubiquitous aspect of pharmacokinetics and PKQuest has provided a number of different procedures for handling it. For example, the propranolol pharmacokinetics [1] were described in terms of "ktiss" (tissue/blood partition coefficients) and "freepl" (the fraction free in plasma). In the application of PKQuest to the volatile solutes [3], fw was described in terms of "Kfwat" (oil/water partition coefficient) and "klip_i" (the fraction of lipid in each organ).

For the protein bound antibiotics it will be assumed that the value of fw_i for organ i can be described by the single site Scatchard type binding equation (see [1] for details):

where c_i is the free concentration in organ i, k is the protein binding constant and Pb_i is the concentration of protein binding sites in organ i. For the special case of linear binding (no saturation), kc_i<<1, eq. 3 reduces to

As is the case for other beta-lactam antibiotics [6,10], it will also be assumed that albumin is the binding protein so that the protein binding site concentration in organ i (Pb_i) is proportional to the extravascular albumin concentration in organ i. In PKQuest, the default values for the tissue protein concentrations (cProt_i) relative to plasma have been preprogrammed. These values are based primarily on the measurements of Tsuji et. al. [6] for the rat. (The user can change these values by entering values for cProt_i.) Only the experimental value of Pb of plasma needs to be entered in PKQuest and the value of Pb_i for the different organs are then calculated using these stored default values.

For the general case (eq. 3), the PKQuest protein binding is characterized by 2 parameters: kProt (the binding constant, k) and cProt_vein (the concentration of binding sites in venous plasma, Pb). The special case of linear albumin binding is completely described by just the one parameter k*Pb (see eq. 4). In PKQuest, the linear case is turned on by entering fw [vein] (the fraction free in the vein plasma, which is independent of concentration) and setting kProt = -2 and the following procedure is used to find the default values of fw_i for each organ i. First, eq. 4 for i=vein is solved for the value of kPb_vein. Then, using the default values of albumin concentration in each organ (cProt [i]), the value of kPb_i is found, and, from eq. 4, the corresponding fw_i determined.

Experimental pharmacokinetic data

Three set of data from previous publications were used. The data for inulin was based on the experimental measurements of Odeh et. al. [11] in which the venous plasma inulin was measured following a 5 minute, constant intravenous infusion of 4 gm of inulin. The data from subject #1 was used (42 year old normal female, weight 87.3 Kg, height 173 cm). The data for dicloxacillin was obtained from the measurements of Lofgren et. al. [12] of the venous plasma time course following a 30 minute constant infusion of 2 gms dicloxacillin. The averaged data from 6 young males (average weight 75 Kg) was used. The data for ceftriaxone was obtained from the measurements of Stoeckel and colleaques [13,14]. The data are for a single subject (M.Fl.) given 4 different IV doses of ceftriaxone – 0.15, 0.5, 1.5 and 3 gms as a 5 minute constant infusion. The experimental data points were obtained by using UN-SCAN-IT (Silk Scientific Corporation) to read the data from the published figures. All the figures shown in this paper are direct copies (in jpeg format) of standard PKQuest output.

Standard human parameters

The default standard values ("standardhuman") are stored as a Maple procedure in PKQuest. The values used for organ flows, volumes, etc. are identical to those used in all the other applications of PKQuest [1-3]. Table I lists the values of organ weight and the blood flow per organ weight for each organ for the standard human (70 Kg). These organ weights are for the default value of 20% body fat. They are scaled depending on the value of "Fat" that is input. The "portal" compartment corresponds to all the organs drained by the portal vein (stomach, small and large intestine, pancreas and spleen) with a blood flow equal to that in the portal vein. The "liver" blood flow corresponds to the hepatic artery. The compartment labeled "other" groups all the other organs with a flow and weight adjusted to account for the total body weight (70 Kg) and the total default cardiac output (6.06 liters/min). For a complete listing of all parameters and constants used in PKQuest, download the file gensolve.mws from the PKQuest web site http://http:\\www.pkquest.com and view the routines "standardman()" and "defaultpar()".

Table 1.

Organ weights and blood flows for standard human (70 Kg, 20% fat)

Organ	Weight (Kg)	Blood Flow (lit/min/Kg)
Artery	1.1	----
Vein	4.4	----
Liver	1.8	0.25 (hepatic artery)
Portal	1.5	0.75 (portal vein)
Kidney	0.31	4.0
muscle	33.0	0.0266
brain	1.4	0.56
heart	0.33	0.8
lung	0.536	14.98
skin	2.6	0.12
fat	14	0.056
"other"	4.12	0.054
"bone"	4.90.	0.0

Results

Inulin

As described previously [1], the PBPK data unique to each solute is input to PKQuest in the form a short Maple http://http:\\www.maplesoft.com procedure that completely characterizes the pharmacokinetics:

inulin:=proc()

   defaultpar():

   Wtot:=87.3;

   standardhuman(Wtot);

   Fat:=0.28; # 26% Fat by weight based on 173 cm height.

   mecf:=1.0; # Inulin distributes only in default extracellular space

   fclear [muscle]:=0.354; # permeability value for muscle, all other organs set from it

   rclr:=0.1; #Renal water clearance of 0.10 liters/min

   cunit:="milligrams"; #unit used in printed and plotted output

   concunit [vein]:=4;# input data = venous plasma concentration

   ninput:=1; finput[1]:=table([organ=vein, type=1, rate=800, tbeg=0,

      tend=5, csteady=0, padjust=0]); # 5 minute constant infusion of 4000 mg

The experimental data was for the subject in fig. 2 of Odeh et. al. [11] (this female had a weight and height of 87.3 Kg and 173 cm, and a predicted 28% fat content). There are 3 parameters that specifically characterize inulin: mecf, rclr, and fclear [muscle]:

Figure 2.

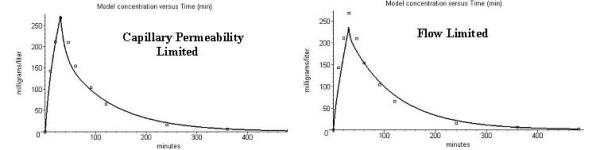
Comparison of the model prediction (solid line) and the experimental data (squares) for dicloxacillin venous plasma concentration. Left panel: Capillary permeability limitation (fclear_muscle 0.26). Right panel: Flow limited – no permeability limitation (fclear_muscle = 1.0).

The parameter mecf determines the extravascular volume of distribution. The default value is mecf = -1, which indicates that the solute distributes in all the body water. If mecf is >0 then the solute distributes in organ i in a water volume equal to mecf*ecf [i] where ecf [i] is the default extracellular space for organ i. The user has the option to either adjust each of the individual values of ecf [i], or scale all the values by the factor mecf. The default ecf [i] values in "standardhuman" were initially set equal to the values directly determined in the rat by Tsuji et. al. [6] from steady state tissue inulin measurements. Then, the value of mecf that optimized the fit to this data of Odeh et. al. was determined, and these new values were chosen for "standardhuman". (The human values were 16% larger than the rat values). Since the default data was chosen to fit this data, setting mecf = 1 simply selects this optimized data.

The parameter rclr is the free water concentration renal clearance. It is equal to the volume of blood water cleared per min (liters/min). It differs slightly from the standard renal clearance which is equal to plasma volume/min (rclr = 0.94 × plasma clearance). The value of rclr of 0.1 liter/min corresponds to the value directly measured by Odeh et. al. for this subject.

The user has two different options for entering the values of fclear [i] (see eq. 1). If, as in this case, just the value of fclear [muscle] is input, then PKQuest will, by default, use the relation in eq. 2 to determine the value of PS_muscle; use the default ratios of PS_i/PS_muscle to determine the value of PS_i for the other organs, and then use eq. 2 to find the corresponding flcear [i] for the other organs. The default ratios PS_i/PS_muscle assume, for example, that the liver and kidney have a high permeability and are flow limited, while, because of the blood brain barrier, the brain capillary permeability is zero. The user can also individually input the value of fclear [i] for any organ i. If an organ's value for fclear is not set, then PKQuest will use the value set from the above calculation based on the muscle value. The parameter fclear [muscle] was adjusted to find the best fit to the inulin data using the Powell minimization feature of PKQuest [1]. The optimal value of fclear_muscle was 0.354.

Figure 1 shows the PKQuest output for this inulin data (all the figures in this paper are copied directly from the standard output of PKQuest). There is good agreement between the predicted venous plasma concentration (solid line) and the experimental values (squares). PKQuest also routinely outputs the experimental pharmacokinetic clearance and volume of distribution determined from the first and second moments of the plasma concentration extrapolated exponentially to infinite time [15]. These experimentally derived values are in good agreement with the model values: Plasma clearance: 0.104 liters/min (experimental) versus 0.1 (model); Volume of distribution: 10.7 liters (experimental) versus 10.7 (model). PKQuest also outputs the values of fclear [i] and the corresponding value of PS_i determined from eq. 2. The fclear [muscle] of 0.354 corresponds to a PS of muscle of 0.6 ml/min/100 gm.

Figure 1.

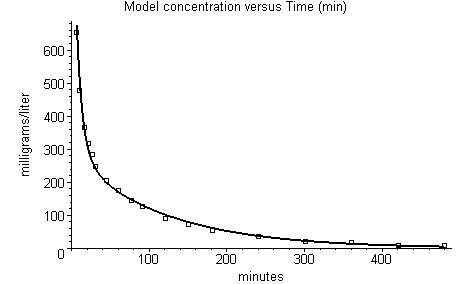
Comparison of the model prediction (solid line) and the experimental data (squares) for inulin venous plasma concentration.

Dicloxacillin

Approximately 97% of human serum dicloxacillin is protein bound (fw_B = 0.03) [16], making it a likely candidate to show some permeability limitation. Another advantage of dicloxacillin is that this binding is linear, showing no evidence of saturation at concentrations up to 230 mg/liter [6,16], simplifying the PBPK. Since the binding does not saturate, it can be described by eq. 4 and the binding is characterized by the single parameter fw [vein] (see Methods).

The complete Maple procedure for dicloxacillin is:

dicloxacillin:=proc()

   defaultpar():

   Wtot:=75.0;

   standardhuman(Wtot);

   Fat:=0.16;

   concunit [vein]:=4;

   mecf:=1.0;

   kProt:=-2; #this turns on use of cProt [i] to determine fw [i]

   fw [vein]:=0.03;

   rclr:=0.12; # renal filtraton clearance

   Tclr [kidney]:=3.0;# Renal tubule secretion clearance

   fclear [muscle]:=0.26;

   ninput:=1; finput[1]:=table([organ=vein, type=1, rate=2000.0/30, tbeg=0,

      tend=30, csteady=0, padjust=0]); # constant 30 minute infusion of 2 gms

The data of Lofgren et. al. [12] for the venous plasma time course of normal young males given a 30 minute constant infusion of 2 gms dicloxacillin was used as input. The average body weight for this group was 75 Kg, and the standard fat content for young males (16%, [17]) was assumed. The parameter mecf is set = 1 because dicloxacillin, like inulin, distributes only in the extracellular space as shown by its negligible distribution into red cells and its low blood/tissue partition coefficient [6]. This means that dicloxacillin has the same volume of distributions in the different organs as was used above for inulin. Dicloxacillin is cleared primarily by the kidney in these subjects [12] and there is a large component of renal tubular secretion that is blocked by probenecid [18] determined by the parameter Tclr [kidney]. (Other studies have indicated that the liver can account for 40% or more of the total clearance [16]. PKQuest calculations (not shown) based on the assumption that the clearance was divided equally between the kidney and liver yield almost identical results). The value of renal filtration (rclr) was set to the normal value of 0.12 liters/min. The capillary permeability limitation is characterized by the single parameter fclear [muscle] (from which the permeabililty of the other organs is calculated by PKQuest). The above values of Tclr [kidney] = 3.0 (liters/min) and fclear [muscle]:= 0.26 (dimensionless) were obtained by simultaneously optimizing both values using the Powell minimization procedure in PKQuest [1] to find the values that provided the best fit to the experimental data.

The left hand panel in figure 2 shows a comparison of the PKQuest model predictions (solid line) for this set of input parameters with the experimental data of Lofgren et. al. [12]. Again, the agreement is quite good. This model fit used a permeability limitation (fclear) for muscle of 0.26. This means that the venous blood leaving the muscle is 26% equilibrated with the tissue. Using eq. 2, this corresponds to a PS_muscle of 13 ml/min/100 gm.

The right hand panel in figure 2 shows the best fit that can be found for this same data, assuming that dicloxacillin is flow limited (fclear = 1). The fit is clearly worse, especially at the early time points where a permeability limitation should be important. Part of the better fit may have resulted from adjusting 2 parameters (fclear [muscle] and Tclr [kidney]) for fig. 2 (left), while, in fig. 2 (right), only one parameter was adjusted (Tclr [kidney]). However, the fact that the fit in fig. 2 (right) could not be significantly improved by trying to adjust other parameters, such as muscle blood flow, extracellular space and/or plasma protein binding, suggests that this permeability limitation is real.

Ceftriaxone

In addition to having a high degree of protein binding, Ceftriaxone has the additional complication that this binding is non-linear and saturates at high concentrations. Stoeckel and colleagues have carried out detailed investigations of the pharmacokinetics of ceftriaxone in humans and the influence of this non-linear binding [13,14]. They showed that the non-linear kinetics of ceftriaxone arise solely from this non-linear binding by demonstrating that the kinetics became linear if the free drug concentrations are used in the pharmacokinetic calculations. In this section, PKQuest will be used to develop a PBPK model for this data. The model includes both non-linear binding and a permeability limitation, the first time that both these factors have been included in a PBPK.

Because the protein binding saturates, the general Scatchard binding equation (eq. 3) must be used. This requires a value for the protein binding constant (k) and the concentration of binding sites in each organ (Pb_i). As described above (Methods), these constants are determined by two PKQuest parameters: kProt (the association constant for protein binding) and cProt [vein] (the plasma concentration of binding sites). PKQuest then uses the default information about the tissue albumin concentration in each organ relative to the plasma albumin to determine the concentration of binding sites in each organ (Pb_i). The data of Stoeckel et. al. [13,14] are ideal for this analysis because they provide information about the venous blood levels for the same subject (M.Fl.) given 4 different IV doses of ceftriaxone – 0.15, 0.5, 1.5 and 3 gms. It is important to have these different inputs in order to test if the PBPK can accurately model the non-linear kinetics. Since all the doses were given to the same subject, an identical set of PBPK parameters is used for all the doses:

ceftriaxone:=proc()

   defaultpar():

   Wtot:=70.0; #Body weight

   standardhuman(Wtot);

   Fat:=0.18;# Fat body weight fraction for 70 Kg, 183 cm man.

   cunit:="micromoles";

   concunit [vein]:=4;# input = venous plasma concentration

   mecf:=0.85; # distribute only in extracellular space – adjusted to fit data

   fclear [muscle]:=0.15; # determinse muscle capillary permeability

   rclr:=0.11; # Normal renal clearance

   Tclr [kidney]:=0.035; # Renal tubule secretion

   Tclr [liver]:=0.06; # Liver metabolism

   cProt [vein]:=806; # total conc. protein binding site in plasma (micromoles/liter)

   kProt:=0.0315; # Association constant (liters/micromoles)

Subject M.Fl. had a weight of 70 Kg and height of 183 cm (K. Stoeckel, personal communication). The values of cProt [vein] and kProt used above are the values determined by equilibrium dialysis for the subject M.Fl. [13]. Ceftriaxone is eliminated by both renal secretion and liver metabolism. The normal value of 0.ll liters/min was used for renal clearance, and the tubule secretion (Tclr [kidney]) and liver metabolism (Tclr [liver]) were adjusted to have a renal clearance of about 65% of the total clearance as was observed experimentally. The liver metabolism and tubule secretion were assumed to be linear because the kinetics were linear if corrections were made for the plasma binding. The value mecf has been set to 0.85 to slightly improve the fit to the data. This makes the extracellular volume of distribution 85% of the default value. It is not clear whether this has some physiological significance for this subject or if it is just a "fudge" factor that corrects for some other limitation in the PBPK. The two parameters fclear [muscle] and Tclr [liver] were simultaneously adjusted using the Powell minimization procedure in PKQuest to obtain the best fit to the experimental data. For this case, where the binding is non-linear, the value of fclear [muscle] that is input is interpreted as the value of fclear in the limit of zero concentration. As the concentration increases, the value of the fraction free (fw_B) will increase (eq. 3) and the corresponding value of fclear (eq. 2) will also increase (i.e. become less permeability limited). The optimized value of fclear [muscle] of 0.15 corresponds (see eq. 2) to a PS_muscle of 6 ml/min/100 gm.

Figure 3 shows the agreement between the model predictions of PKQuest and the experimental data for inputs of 0.15, 0.5, 1.5 and 3.0 grams. The same parameter set was used for each of these 4 fits. Only the input function was varied. Over the plasma concentration ranges seen at early times for each of the 4 doses, the fraction free in the blood and the fclear_muscle (fraction of solute that equilibrates with the tissue in one pass through the muscle capillary) varies as follows: At 0 μM: fraction free = 0.038, fclear = 0.15; At 50 μM: fraction free = 0.092, fclear = 0.33; At 150 μM: fraction free = 0.18, fclear = 0.55; At 450 μM: fraction free = 0.374, fclear = 0.8; At 800 μM: fraction free = 0.51; fclear = 0.89. The non-linearity in the kinetics is apparent both in the changes in the qualitative shape of the curve and in the absolute values of the plasma concentration. The agreement between the model and experiment for this 20 fold dose range and roughly 10 fold range of fraction free is surprisingly good, especially considering that there are so few adjustable parameters (see below).

Figure 3.

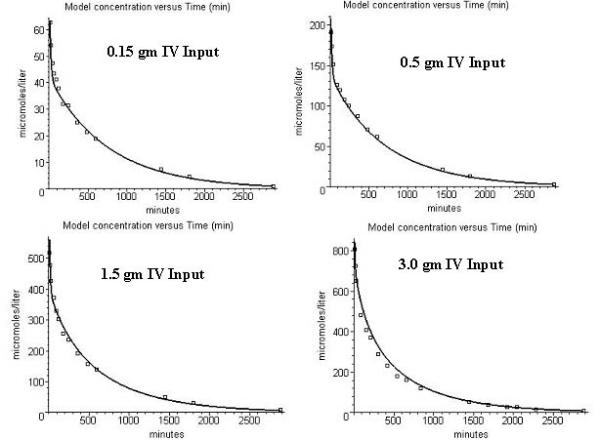
Comparison of the capillary permeability limited model prediction (solid line) and the experimental data (squares) for ceftriaxone venous plasma concentrations. The four panels correspond to inputs of 0.15, 0.5, 1.5 and 3.0 grams given as a 5 minute constant IV infusion. Because the protein binding saturates, the effective capillary permeability limitation (fclear) decreases as the concentration increases.

Figure 4 show the corresponding fits for the case where ceftriaxone is assumed to be flow limited (fclear = 1) for the 0.15 and 3.0 gm dose. Comparing figures 3 and 4 it can be seen that the permeability limitation significantly influences the pharmacokinetics only for the lower doses because of the saturation of the protein binding. For the low dose (0.15 grams), the plasma concentration at early times is about 50 μM which will have a corresponding fclear of 0.33. This means that there will be only 33% equilibration during one pass through the capillary – a significant permeability limitation. However, for the high dose (3.0 grams), the early plasma concentration is about 800 μM which corresponds to a fclear of 0.89 which differs only sightly from the flow limited condition (fclear = 1) assumed for figure 4.

Figure 4.

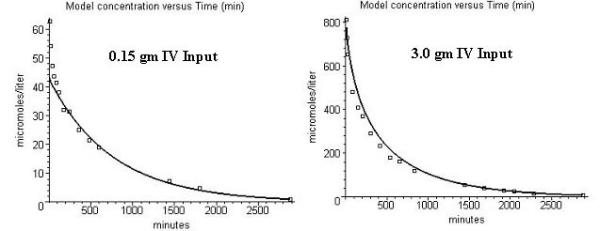
Comparison of the flow limited model prediction (solid line) and the experimental data (squares) for ceftriaxone venous plasma concentrations. Left panal: 0.15 gm IV input; Right panel: 3.0 gm input.

Discussion and Conclusions

The definition that is introduced in this paper for capillary-tissue clearance (fclear, eq. 1) and its relation to the fraction free in tissue (fw_B, eq. 2) is not new. These definitions are identical to the classical expressions used to describe pulmonary diffusion capacity of a gas where fw_B corresponds to the inverse of the gas solubililty (β) [19]. The capillary permeability limitation produced by the protein binding of dicloxacillin and ceftriaxone described in this paper is directly analogous to the carbon monoxide pulmonary diffusion limitation that results from its high blood solubility. This analogy has not been previously recognized for the protein bound antibiotics.

The value of PS_muscle of inulin determined above is a measure of the capillary permeability averaged over all the muscles. It represents the permeability for the muscle in the condition of these measurements – the resting human with a relatively low muscle blood flow (default value = 0.0266 liters/min/Kg). Surprisingly, this may be the first report of this value in humans. The value of PS_muscle found here for inulin of 0.6 ml/min/100 gm is slightly less than the reported value of 0.9 for lightly exercising in vivo human forearm muscle [20] and is in the range reported for animal measurements (0.6 to 1.2; [5]). The literature values are for muscles with 2 to 4 times the default blood flow assumed for these measurements. Since the muscle capillary surface area (S) can vary by a factor of more than 4 as capillaries are recruited at higher flows [5], this low resting blood flow could easily account for the low PS inulin value obtained in this analysis.

The values of PS_muscle for dicloxacillin and ceftriaxone estimated here are the first measurements of the capillary permeability for any antibiotic. In fact, as discussed above, it had always been assumed previously that these drugs were flow limited, which would mean that their permeability was so large that it could not be measured. These drugs do, in fact, have a high intrinsic permeability. For example, the value of PS_muscle found for dicloxacillin of 13 ml/min/100 gm is a very high permeability and, if it were not protein bound (and fw_B equaled 1), would correspond to an fclear [muscle] of 0.999 (see eq. 2) – i.e. it would be flow limited. The only reason that it is not flow limited and that its value can be measured is because of its high protein binding, with a fw_B of 0.03. The value of PS_muscle found for ceftriaxone (6 ml/min/100 gm) is about half the dicloxacillin value.

The PS_muscle values for the antibiotics are about 10 times larger than the PS value of inulin. If these antibiotics were lipid impermeable and had to cross the capillary via the interendothelial cell slits, their permeability should be determined simply by their molecular radius [5], and they should have a permeability similar to that of sucrose or EDTA, molecules with similar molecular radii. The antibiotic skeletal muscle capillary permeabilities found here are about 2 times larger than those reported for sucrose and EDTA [5]. It has recently been shown that the β-Lactam antibiotics are transported across the intestinal epithelial cells via the peptide transport system [21]. This relatively high capillary permeability for these antibiotics may indicate that this system is also present in the capillary endothelium.

Does this capillary permeability limitation have any practical significance in terms of therapeutics? The anti-infective activity of the antibiotic should be roughly equivalent to the free concentration in the tissue water [22]. Figure 5 contrasts the time course of the free ceftriaxone concentration in the extracellular muscle (black) and plasma (red) water for the permeability limited (solid line) and flow limited (dashed line) cases. For the low dose (0.15 gram) where the protein binding is high and the permeability limitation is at its maximum, the muscle water antibiotic concentration for the permeability limited case (black solid line) is significantly less than for the flow limited case (black dashed line) for the first 30 minutes. After 40 minutes the muscle tissue concentrations for the permeability limited and flow limited cases are not significantly different. At the high dose (3.0 gram), there is no significant difference even at early times. Thus, from a therapeutic viewpoint, this permeability limitation is probably not important.

Figure 5.

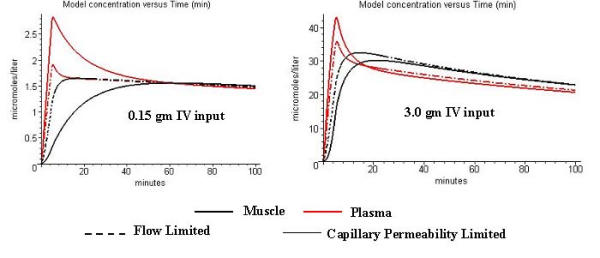
Free plasma (red) and tissue (black) water ceftriaxone concentration. The dashed lines correspond to the flow limited model results and the solid lines are for the case of a capillary permeability limitation. The PBPK parameters and input conditions are identical to those used in figs. 3 and 4.

This inference of a capillary permeability limitation is indirect since it is based only on a theoretical analysis of the experimental plasma pharmacokinetics. The analysis shown in fig. 5 suggests that it should be possible directly observe the effects of this permeability limitation from simultaneous measurements of the free water concentration in the plasma and muscle. The low dose (0.15 gram) panel in fig. 5 shows that the capillary permeability limitation creates a large difference between the plasma (red line) and muscle (black line) free water concentration during the first 30 minutes. Kovar et. al. [22] measured the ceftriaxone free plasma and muscle water using microdialysis in the rat for doses of 50 and 100 mg/Kg. They compared their experimental measurements with theoretical pharmacokinetic curves based on the flow limited assumption. For the low dose (where binding and permeability limitation will be higher) the experimental muscle water concentration at 50 minutes was significantly less (about 40%) than the flow limited prediction and this difference became insignificant by 100 minutes. Similarly, the muscle tissue measurements of Tsuji et. al. [6] of cefazolin (another protein bound antibiotic) were significantly less than the flow limited predictions for the first 100 minutes. Although both of these results are consistent with a capillary permeability limitation, they are probably not conclusive because of the large scatter in the measurements and the inherent uncertainties and limited time resolution of the tissue measurements.

The PBPK for ceftriaxone discussed in this paper would normally be thought of as very "difficult" or "complicated". The model requires information for each organ about the extravascular volumes of distribution, protein binding constants, capillary permeability, weights and blood flows, in addition to information about renal clearance, tubular secretion and hepatic metabolism. One would expect that, with this many parameters, it would be impossible to have any confidence in the PBPK parameters that are found. However, because of the basic design feature of PKQuest, there are actually only 6 parameters that are specifically required to completely characterize ceftriaxone (rclr, Tclr [liver], Tclr [kidney], cProt [vein] and kProt; see the ceftriaxone procedure above). Two of these parameters were measured experimentally (cProt [vein] and kProt) and the value of rclr (renal plasma clearance) was set to the default human value. Since the ratio of liver to renal clearance is known experimentally, only one of the parameters Tclr [liver] and Tclr [kidney] is independent. This leaves just two adjustable parameters (fclear [muscle] and Tclr [liver]). In addition, it may be necessary to slightly adjust some of the default parameters (e.g. mecf for the ceftriaxone case) to optimize the fit.

These PBPK studies provide a good example of the major difference of philosophy between PKQuest and the usual PBPK. For example, in the rat PBPK developed by Tsuji et. al. [6] for cefazolin, nearly every PBPK parameter required by the model was directly measured, including steady state extravascular volumes of distribution in the different organs, organ blood flows and weights, renal and hepatic clearance, time dependence of cefazolin concentration in the different organs, etc. This approach is, for obvious reasons, impossible for human studies. The basic philosophy of PKQuest is that it is not necessary to make these measurements for each drug that is investigated if the PBPK has been previously tested and refined using a large variety of compounds, combined with information available in the literature. For example, for these studies, the extracellular volumes of distribution (ecf) determined in the inulin PBPK analysis have been used as the default values for the antibiotic studies. As PKQuest is applied to other compounds, these "default" value will be improved and modified. The more that PKQuest is used, the more reliable are its values and the more confidence one can place in its results.

The major design feature of PKQuest, which is to minimize the number of input parameters required from the user, and maximize the use of previously determined information, supports this philosophy. For example, the user only needs to enter the value of fclear [muscle] and PKQuest uses the previously determined ratios of PS_i/PS_muscle to set all the other organ permeabilities. As another example, the user need only enter the one parameter mecf to set all the extracellular volumes for each organ and the user knows that a mecf of 1 corresponds to the standard default human set of values. If the user wanted, e.g. to make the ecf of muscle 10% larger than the default, it is only necessary to enter ecf [muscle] = 1.1*ecf [muscle] and the user does not need to know the actual default value. This not only makes PKQuest easier to use, but it also improves the validity of the final PBPK because the user has confidence that the best estimates based on previous applications of PKQuest are being used.

The PKQuest program and all of the examples used in this paper are freely available on the Web at http://http:\\www.pkquest.com.

Competing Interests

None.

Pre-publication history

The pre-publication history for this paper can be accessed here:

http://www.biomedcentral.com/1472-6904/2/7/prepub