Untangling Ligand Induced Activation and Desensitization of G-Protein–Coupled Receptors

Abstract

Long-term treatment with a drug to a G-protein–coupled receptor (GPCR) often leads to receptor-mediated desensitization, limiting the therapeutic lifetime of the drug. To better understand how this therapeutic window might be controlled, we created a mechanistic Monte Carlo model of the early steps in GPCR signaling and desensitization. Using this model we found that the rates of G-protein activation and receptor phosphorylation can be partially decoupled by varying the drug-receptor dissociation rate constant, k_off, and the drug's efficacy, α. The maximum ratio of G-protein activation to receptor phosphorylation (GARP) was found for drugs with an intermediate k_off value and small α-value. Changes to the cellular environment, such as changes in the diffusivity of membrane molecules and the G-protein inactivation rate constant, affected the GARP value of a drug but did not change the characteristic shape of the GARP curve. These model results are examined in light of experimental data for a number of GPCRs and are found to be in good agreement, lending support to the idea that the desensitization properties of a drug might be tailored to suit a specific application.

INTRODUCTION

As a general rule, ligands cause both receptor-mediated signaling and signal desensitization. In the case of G-protein–coupled receptors (GPCRs), a ligand signals by activating a receptor, which in turn activates a second messenger(G-protein) inside the cell. By holding the receptor in the active state, the ligand also targets the receptor for phosphorylation—a key first step in the desensitization pathway.

In this work we use Monte Carlo simulations of ligand-induced GPCR signaling and desensitization to learn how these two processes are related and suggest new directions for drug design. Historically drug development has focused primarily on finding drugs that cause a response in the short term, viewing longer-term, drug-induced desensitization as a side effect. However, receptor activation and desensitization are intimately related processes that must both be considered when developing a useful drug. For example, the highly potent μ-opioid receptor agonist etorphine is not a medically useful drug because it can only be used a few times before the body becomes desensitized to the drug (Yu et al., 1997). By better understanding how drug properties affect signaling and desensitization, we hope to guide drug development efforts toward new drugs with fewer side effects and a greater range of therapeutic applications.

In a classical view of drug action, receptor signaling and desensitization are simply related; however, experimental data in a variety of systems indicate that the relationship is more complex. According to the classical view, any changes to a ligand that increase its ability to signal would also increase the amount of receptor phosphorylation caused by the ligand. In contrast, experimental measurements of activation and desensitization for the three different receptor systems shown in Fig. 1 indicate that this simple relationship does not hold for a number of well-studied cases. Similarly, ligand-induced activation and desensitization are not simply related in the dopamine D₁ (Balmforth et al., 1990; Barton and Sibley, 1990) and N-formyl peptide receptor systems (Riccobene et al., 1999), although in these systems the deviation is less severe. Therefore, in many receptor systems, ligand-induced signaling is a poor predictor of the ligand's desensitization ability.

FIGURE 1.

Comparison of activation and desensitization profiles for a variety of drugs (circles) in three different receptor systems. (a) β₂-adrenergic receptors in a reconstituted membrane system (Benovic et al., 1988). (b) Dopamine D_1A receptor in C-6 glioma cells (Lewis et al., 1998). (c) μ-Opioid receptors in Xenopus oocytes (Yu et al., 1997).

If receptor signaling is not the primary determinant of ligand-induced desensitization, then what is? For a given signaling pathway in a particular cell type, the ability to differentially regulate activation and desensitization must rest with the ligand itself. Here we test the hypothesis that the ligand's binding kinetics and ability to activate a receptor conspire to differentially regulate desensitization and activation. This connection suggests a relatively simple approach to decoupling desensitization and activation via changes in ligand-specific properties.

Mechanism of GPCR signaling and desensitization

For GPCRs, the mechanism of ligand-induced activation and desensitization can be divided into the three steps shown in Fig. 2. In the first step (Fig. 2 A), a ligand binds to the receptor to stabilize a specific receptor conformation. A common approximation is to assume that the receptor rapidly oscillates between an inactive conformation (R) and an active conformation (R^*). In this view, a ligand signals by biasing the receptor to spend more time in a particular conformation. This ligand-induced bias is controlled by the drug's conformational selectivity factor, α, which roughly corresponds to a drug's efficacy and will figure prominently in this work.

FIGURE 2.

Three processes that affect GPCR desensitization. (a) Receptors sense the environment via ligand binding. The ratio of ligand-bound receptors in the active state vs. inactive state is determined by the receptor activation equilibrium constant, K_ACT, and the ligand-specific conformational selectivity factor, α. (b) Active receptor conformations can bind to and activate the G-protein trimer. Because the G_α subunit possesses an intrinsic GTPase activity, with time the subunit will cleave GTP into GDP, thereby allowing the inactive G_α subunit to recombine with G_βγ to recover the inactive G-protein. (c) Receptor desensitization is initiated by RK binding to the active G_βγ subunit of the G-protein. This complex can then phosphorylate the active receptor, targeting the receptor for internalization and desensitization. Note that the ligand binding and G-protein activation properties of the receptor are the same independent of the receptor's phosphorylation state.

In the second step (Fig. 1 B), the active receptor binds to and activates a G-protein in the cell membrane. In the inactive state, G-proteins exist as a GDP-bound trimer. Upon activation by a receptor, the G-protein exchanges GDP for GTP and breaks into two signaling subunits, G_α-GTP and G_βγ. In most G-protein species, the active G_α-GTP protein is thought to dissociate from the membrane to activate cytosolic targets (Evanko et al. 2000). Due to an intrinsic GTPase activity of the G_α subunit, G_α-GTP reverts to an inactive G_α-GDP which then can rebind with the membrane bound G_βγ subunit to recover the inactive G-protein. Using this mechanism the cell is able to detect and amplify small signals and also reset when the signal is removed.

In the third step (Fig. 1 C), the active receptor is phosphorylated and targeted for desensitization. The active G_βγ subunit is able to recruit a receptor kinase to the membrane. Once attached to the membrane, the receptor kinase can phosphorylate receptors and in doing so target them for arrestin binding and eventual internalization (Krupnick and Benovic, 1998). It is believed that only receptors in the active conformation are phosphorylated because other, inactive receptor species present in the cell membrane that are also subject to phosphorylation are not internalized when their ligand is absent (Bunemann et al., 1999). Other parallel desensitization pathways involving PKA and PKC also exist (Chuang et al., 1996), but these pathways are poorly understood and are thought to play a less important role in desensitization and therefore are not included in our analysis.

GPCR desensitization as a spatially dependent and discrete process

The early steps of desensitization are likely best represented as spatially dependent and discrete. Because many of the reactions that mediate desensitization take place within the membrane, reaction rates depend not only on the intrinsic interactions between species, but also on the rates of diffusion to bring species together. In practice, diffusion limitations often play a dominant role in limiting the overall reaction rate between species within the membrane, adding an inherently spatial component to the desensitization reaction (Lauffenburger and Linderman, 1993). As a result, in systems where diffusion is slow, reactions tend to depend strongly on the local rather than global concentration of each species.

When diffusion rates are limiting, desensitization also becomes a more discrete process. Because slow diffusion rates limit the pool of reactive species to a small local area, the total number of reactive species drops. At these low numbers, the discrete identity of each protein plays a more significant role. For example, if diffusion is slow, then the recruitment of one receptor kinase to the cell membrane will strongly affect the phosphorylation rates of nearby receptors, but will not affect the phosphorylation rates of distant receptors. Because proteins are discrete, there is a finite probability that the receptor kinase will phosphorylate all of the local receptors and have no further effects.

From a modeling perspective, the discrete and spatially dependent phenomena associated with desensitization can be included by using a Monte Carlo (MC) model, as is done in this work. This MC model simulates the reaction and diffusion events of discrete particles as a stochastic process. It is important to note that although MC models can simulate discrete and spatially dependent reactions, they can also model conditions where diffusion is not limiting and particles behave in a more continuous way. Thus, MC models provide a mechanistic technique to simulate reactions under broader conditions than can be described using classical mass action kinetics, and as such are expected to better represent biological reactions within the cell membrane.

An MC simulation of a similar local, discrete behavior has been demonstrated for G-protein activation (Mahama and Linderman, 1994). These simulations examined the importance of ligand movement among surface receptors, sometimes termed “switching” (Stickle and Barber, 1989). To understand switching, consider the three ligand-binding regimes described in Fig. 3. At one extreme, a ligand molecule binds a receptor with a very small ligand dissociation rate constant (k_off), thereby forming a long-lived receptor-ligand complex that exhibits nearly no switching (Fig. 3 A). Under these conditions, the receptor activates all local G-proteins to form a diffusion-limited zone that is depleted of inactive (or “activate-able”) G-proteins and enriched in G_βγ surrounding the receptor. At the other extreme, a ligand molecule binds receptors with a large k_off value, thereby forming short-lived receptor-ligand complexes that exhibit strong switching behavior (Fig. 3 C). Under these conditions, ligand movement among receptors allows smaller, more homogeneous G_βγ enrichment zones to form. Between these two extremes are ligands that bind with an intermediate value of k_off and exhibits some switching behavior (Fig. 3 B). Ligands in this intermediate state exhibit a distribution of local G_βγ enrichment zones, which will become important later when describing how the receptor phosphorylation rate changes with k_off.

FIGURE 3.

The process formation of enrichment zones of G_βγ as a function of the k_off value of a ligand. (a) At low k_off values, a low concentration ligand will tend to fully activate only a few receptors. This local activation will cause a significant depletion of inactive G-proteins and a concomitant enrichment in G_βγ around a few receptors, although leaving most receptors untouched. (b) Intermediate k_off values cause the G_βγ enrichment zones to become somewhat more homogeneous, but smaller. (c) Large k_off values result in a more homogeneous distribution of smaller G_βγ enrichment zones surrounding the receptor. Note that G_βγ enrichment zones correspond to inactive G-protein depletion zones because inactive G-proteins are consumed to generate G_βγ.

Previous work has indicated that increased ligand switching will lead to an increase in overall G-protein activation (Mahama and Linderman, 1994; Shea and Linderman, 1997). By rapidly switching receptors from the active to inactive states, ligands with large k_off values cause less G-protein activation per ligand binding event, but more activation overall due to the reduced influence of diffusion limitations surrounding the receptor. These simulation results have been corroborated by some experimental findings (Mahama and Linderman, 1995; Stickle and Barber, 1989, 1992), although more experimental work needs to be done to establish their generality.

We hypothesize that switching effects also play a prominent role in controlling receptor desensitization. Like G-protein activation, receptor phosphorylation is governed by reactions between membrane-bound species and as such is likely to be diffusion-limited. In addition, G-protein activation and receptor desensitization are sequentially linked because the G-protein must be activated before receptor kinase can be recruited to the membrane (see Fig. 2). Therefore, changes in G-protein activation should affect receptor phosphorylation, although not necessarily at the same time scale.

Previous models of desensitization did not include discrete reactions or spatial effects, and as such were unable to address the effects of the ligand dissociation rate constant that governs switching. For example, a model of desensitization using a simplified ordinary differential equation model of receptor activation and desensitization suggested that the conformational selectivity factor, α, plays a dominant role in controlling both G-protein activation and desensitization (Riccobene et al., 1999). However, in systems such as the dopamine D_1A receptor shown in Fig. 1 B, G-protein activation and receptor desensitization are not easily related and as such cannot be simply explained by the effect of α alone.

We propose that phosphorylation-mediated desensitization and G-protein activation can be differentially regulated in some systems by the interaction of the ligand-specific conformational selectivity factor, α, and the ligand dissociation rate constant, k_off. The extent of this differential regulation depends on the cellular environment. This relationship will first be explored using a computational model of receptor activation and desensitization and results will then be compared to experimental data.

METHODS

To accurately represent the spatial, discrete, and transient dynamics that influence GPCR signaling and desensitization, we chose to use a kinetic two-dimensional MC model. The signaling and desensitization reactions used in the model are shown in Fig. 2. The simulation contained eleven distinct species: R, R_p, LR, LR_p, LR^*, LR_p^*, G, G_α-GTP, G_α-GDP, G_βγ, and G_βγ-RK. Each species is described in more detail in Table 1.

TABLE 1.

Identities and locations of the species used in the model

Species Name	Description	Location
R	Inactive receptor	membrane
Rp	Phosphorylated receptor	membrane
LR	Ligand bound receptor	membrane
LRp	Ligand bound phosphorylated receptor	membrane
LR*	Active ligand bound receptor	membrane
LRp*	Active ligand bound phosphorylatedreceptor	membrane
G	Inactive G-protein trimer	membrane
GαGTP	Active α subunit of the G-protein	cytosol
GαGDP	Inactive α subunit of the G-protein	cytosol
Gβγ	Active βγ subunit of the G-protein	membrane
GβγRK	βγ subunit bound to receptor kinase	membrane

Note that it is assumed that unbound receptors are always inactive, whereas ligand-bound receptors are in a rapid equilibrium between active and inactive states.

Although most species in the model are membrane-bound, G_α-GTP and G_α-GDP are cytosolic. As a result, the location of these two species was not explicitly followed, but instead it was assumed that these proteins were added to a general cytosolic pool. This approximation was made because diffusion through the three-dimensional cytosol should be more rapid than comparable diffusion along the membrane and as such can be assumed to be nearly instantaneous. Receptor kinase, or RK, technically represents a third cytosolic species; however, the dynamics of RK regulation and the concentration of receptor-accessible RK in the cell are currently not known. Therefore, it is assumed that RK comes from a constant concentration pool and thus changes to its population size are not explicitly tracked in the model.

The parameters describing the base case for the reaction and diffusion events of the simulation are listed in Table 2. For the simulation, the kinetic reaction rates were converted into reaction probabilities using standard techniques (Mahama and Linderman, 1994; Shea and Linderman, 1997). Some of these physical parameters are available directly from the literature, whereas others had to be estimated. For example, the receptor kinase association rate constant, k_f-RK, is an estimated composite rate term that includes the product of the intrinsic association rate between RK and G_βγ times the constant concentration of the RK pool. The value of k_f-RK was estimated to be on the same order as the G_α-G_βγ association rate constant, k_d, because in both cases proteins are recruited from the cytosol to bind with G_βγ in the cell membrane. The receptor kinase dissociation rate constant, k_r-RK, was estimated by assuming that the receptor kinase binds to G_βγ with a high equilibrium affinity. Few diffusion coefficients are known specifically for GPCRs, although diffusion coefficients in the range of 10⁻¹¹ to 10⁻⁹ cm² s⁻¹ have been reported for membrane receptors in general (e.g., Barak et al., 1997; Gennis, 1989; Ljungquist-Hoddelius et al., 1991; Niswender et al., 1985; Smith et al., 1999).

TABLE 2.

Parameters used in the model

Constant	Description	Value
L	Ligand concentration	Varied to maintain a receptor occupancy of 2.5%
kon	Ligand association rate constant	108 M−1 s−1 (Lauffenburger and Linderman, 1993)
koff	Ligand dissociation rate constant	Varied from 1 to 10,000 s−1
KACT	Receptor activation equilibrium constant	10−6
α	Conformational selectivity factor	Varied from 105 to ∞
ki	G-protein inactivation rate constant	1 s−1 (Shea et al., 2000; Thomsen and Neubig, 1989)
kd	Inactive G-protein association rate constant	1000 s−1 (#/cell)−1 (Shea et al., 2000)
kr–RK	Receptor kinase dissociation rate constant	100 s−1
kf–RK	Receptor kinase association rate constant	1000 s−1
D	Receptor and G-protein diffusivity in the membrane	10−11 cm2 s−1 (Barak et al., 1997; Gennis, 1989;Ljungquist-Hoddelius et al., 1991; Niswender et al., 1985; Smith et al., 1999)

All parameters are taken from the literature except for the receptor kinase association and disassociation rate constants, both of which are unknown. These values are representative for many signaling systems; however, the given references contain citations to experimental values for specific systems. Note that here the conformational selectivity factor (α) only affects the receptor conformation and not the ligand binding rates to ensure that the ligand-receptor dissociation rate and receptor activation can be controlled independently.

Future experimental work will help to refine the estimates. Note that G-protein activation and receptor phosphorylation are assumed to be diffusion-limited reactions (Shea and Linderman, 1997), and as such are modeled as collision-coupled.

The rate of interconversion between active and inactive receptor states takes place at a short time scale relative to desensitization, and as such was assumed to be in equilibrium, in agreement with experimental observations (Jensen et al., 2001). The equilibrium between active and inactive receptor states was defined by the composite equilibrium constant αK_ACT, where α is the ligand-specific conformational selectivity factor and K_ACT is the equilibrium ratio of active to inactive receptors when no ligand is present. The conformational selectivity factor, α, represents a measure of a drug's intrinsic efficacy with increasing α values corresponding to increasing positive agonism (Kenakin, 2002). Receptors not bound to ligand were assumed to be inactive, corresponding to a physiologically realistic case of negligible constitutive signaling. In agreement with experimental findings (Jin et al., 2000), ligand-bound phosphorylated and nonphosphorylated receptors are assumed to signal with equal activity.

In a living cell, receptor phosphorylation would eventually lead to receptor internalization and desensitization (Krupnick and Benovic, 1998). However, these later desensitization events would take place at a much longer time scale, and as such are not explicitly modeled here. Instead, it is assumed that the rate of receptor phosphorylation is proportional to the desensitization rate.

In every simulation, the ligand concentration is varied to maintain an average value of 2.5% receptor–ligand occupancy independent of the ligand's dissociation and association rate constants. The ligand concentration was set according to the relationship

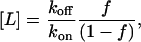where f is the fraction of receptors bound to ligand at equilibrium. Therefore to maintain an average of 2.5% of receptors bound to ligand, f = 0.025. By specifying ligand occupancy this way, it is possible for the instantaneous ligand occupancy to change over the course of the simulation due to the stochastic nature of the model; however, the average receptor occupancy will remain constant.

The simulations were run following a discrete Monte Carlo approach. Physical space was divided into a 3000 × 3000 triangular mesh with periodic boundary conditions. Membrane proteins had a diameter of two grid spacings, with each grid spacing corresponding to a physical distance of ∼2 nm. All simulations were run with 50 receptors and 500 G-proteins, consistent with experimentally observed protein densities (Rousseau et al., 1997; Stickle and Barber, 1989). Time was divided into discrete units shorter than the time required for the fastest event to take place—thereby ensuring that all events take place with a probability <1.

At each time step, a protein was chosen at random and allowed to attempt any of its actions in a random order. The success of the action, such as diffusion or reaction, was determined by calculating the probability of that event occurring in the given time step and comparing that probability to a randomly generated value. Reactions were allowed to take place if less than two grid spacings separated the edges of the proteins. Note that reactions between cytosolic and membrane-bound species are not constrained by the lattice spacing interaction radius because the cytosolic species have no explicit position. The probability of a diffusion event is proportional to the likelihood of a protein with a diffusion coefficient, D, moving one lattice spacing in a single time step. If a diffusion event was accepted within the time step, then the protein was moved one grid spacing in a random direction. If the new site was unoccupied, then the move was made; otherwise, the move was canceled and not retried. If the chosen protein is a cytosolic species, then the diffusion event is ignored.

Initial rates of G-protein activation and receptor desensitization were calculated from average measurements of initial rates. To gather initial rates, the simulation was started with all nonphosphorylated receptors and inactive G-proteins and then run for a small number of iterations (3000) corresponding to between 16 and 60 seconds, depending on the parameters chosen. The value of 3000 iterations was found to be sufficiently long that receptor phosphorylation events were observed, although short enough to gather nonsaturated initial rate data. The initial G-protein activation rate was measured as the slope of the total number of collisions between inactive G-proteins (G) with active receptors (LR^* and LR_p^*) as a function of time. Similarly, the initial rate of receptor phosphorylation was measured as the slope of the total number of collisions between active, unphosphorylated receptors (LR^*) with membrane bound receptor kinase complexes (G_βγ-RK) as a function of time. Linear least squares regression was used to obtain average rates using data from 1000 to 3000 runs per condition. In general, the assumption of a linear initial rate was excellent for the G-protein activation rate (r² values > 0.95) and adequate for receptor phosphorylation rate (r² values > 0.8).

The relative G-protein activation rate and receptor phosphorylation rate were compared in a ratio that we have termed the GARP ratio. The GARP ratio is defined as the initial rate of G-protein activation divided by the initial rate of receptor phosphorylation for a given set of model parameters. GARP values are similar to the relative agonist signaling vs. endocytosis measured experimentally (Whistler et al., 1999) except GARP only follows events at the earliest stages of signal transduction.

Using this model, experiments were run in which a subset of the system parameters was changed to assess its impact on signaling and desensitization. In all cases, the ligand concentration, L, was varied to maintain a constant receptor occupancy level of 2.5%, similar to the physiological levels of many drugs in the body. Because the ligand occupancy was held constant by changing the ligand concentration, the ligand-receptor association rate constant (k_on) was not changed. For each condition, measurements were made for ligand dissociation rate constant (k_off) values ranging from 1 to 10000 s⁻¹. Simulations were run to see the effect of the conformational selectivity factor (α), diffusivity (D), G-protein inactivation rate constant (k_i), and receptor kinase association rate constant (k_f-RK). These simulations were able to show the effect of ligand-specific parameters (α and k_off) and how these behaviors changed with changes in the cellular signaling machinery (D, k_i, and k_f-RK).

Simulations were written in C++ and run on a cluster of Apple Macintosh G4 machines. Each simulated condition took ∼9 h to gather 1000 runs on a single machine. The simulation source code is available upon request from the authors.

RESULTS

Here we demonstrate that changes in ligand-specific and cell-specific properties differentially affect GPCR signaling and desensitization, suggesting that signaling and desensitization can be decoupled in some systems.

Effects of ligand properties k_off and α

Two important parameters that describe the interaction of a ligand with a G-protein coupled receptor are the ligand-receptor dissociation rate constant, k_off, and the conformational selectivity factor, α. Here we report the effects of both of these parameters on G-protein activation and receptor phosphorylation.

As expected, changes in ligand properties change the ligand's ability to signal via G-proteins in the model (Fig. 4 A). Model results agree with experimental data showing that increasing efficacy (α) results in increased G-protein activation (Kenakin, 2002). This increase in G-protein activation due to increased α approaches a limit, however, because at most a receptor can be 100% active—meaning that every encounter between the receptor and an inactive G-protein causes the G-protein to become active. Similarly, increases in k_off also result in increased G-protein activation, as predicted by previous theoretical and experimental work on ligand switching (Mahama and Linderman, 1994; Shea and Linderman, 1997).

FIGURE 4.

Effects of ligand dissociation rate constant, k_off, and conformational selectivity factor, α, on the initial rates of G-protein activation and receptor phosphorylation. Values of α = 10⁵, 10⁶, 10⁷, and ∞ represent ligand-receptor complexes that are active 10%, 50%, 90%, and 100% of the time, respectively. Note that the α = 10⁷ and α = ∞ curves nearly overlap. In all simulations, 2.5% of receptors are occupied by ligand. The data in (a) and (b) are combined into (c) to directly show the relationship between the G-protein activation rate and receptor phosphorylation rate, or GARP value. Parameter values not mentioned are listed in Table 2.

The effects of individual ligand properties on the receptor phosphorylation rate have not been described before, and when simulated yield the surprising results shown in Fig. 4 B. In general, increasing α results in an increased phosphorylation rate for any k_off value. This finding makes sense in light of the increased G-protein activation and hence receptor kinase recruitment to the membrane that accompanies increases in α, and is in agreement with the previous modeling work in the area (Riccobene et al., 1999). In contrast, however, increases in k_off do not always lead to an increase in the receptor phosphorylation rate. This effect is particularly evident at lower α values, where the phosphorylation rate can be clearly seen to pass through a minimum at an intermediate k_off value.

The reason that intermediate values of k_off can cause a minimum in receptor phosphorylation can be understood by examining the spatial distribution of signaling and desensitization processes operating in the cell. The gray enrichment zones shown in Fig. 3 show how the concentration of G_βγ and hence G_βγ-RK is distributed as a function of k_off. At low k_off values, G_βγ-RK forms a large island around the ligand-bound receptor (as in Fig. 3 A), causing the few receptor-ligand complexes to become phosphorylated with nearly 100% probability. As k_off increases, the size of the G_βγ-RK island decreases resulting in a lower probability of a ligand-bound receptor becoming phosphorylated (Fig. 3 B). However, at sufficiently high k_off values (Fig. 3 C), the increase in the number of receptors that can be phosphorylated and the total number of G_βγ-RK present in the system begins to play a dominant role, resulting in a net increase in receptor phosphorylation.

Said another way, at intermediate values of k_off, the ligand remains bound to the receptor for long enough to activate G-proteins, but often not long enough for the active G-proteins to recruit a receptor kinase to the membrane and phosphorylate the receptor. Therefore, at intermediate values of k_off receptor phosphorylation is minimized.

The relative effects of changing ligand properties on signaling and desensitization can be examined by plotting the GARP values as in Fig. 4 C. By directly comparing the G-protein activation rate and receptor phosphorylation rate, we see a clear maximum at intermediate k_off values and low α values. From a drug design standpoint, this maximum predicts that for each value of efficacy there exists an optimal k_off that will maximize signaling although minimizing desensitization.

Effects of cell properties k_i, D, and k_f-RK

Although a ligand's GARP value is clearly dependent on the identity of the ligand, cell-specific parameters are also likely to influence a ligand's signaling and desensitization profile. These differences associated with the cell could help to explain why in some systems activation and desensitization are proportional, whereas in other systems they are not.

To explore the effect of different cell-specific properties, the following three parameters were independently varied: the G-protein inactivation rate constant, k_i; the diffusion coefficient, D; and the receptor kinase association rate constant, k_f-RK. In each case, a ligand's GARP value was calculated for a range of cell-specific parameter values and a range of k_off values to see how the parameter affected G-protein activation and receptor desensitization. In each simulation, one reference case using the parameters listed in Table 2 is included for comparison. The results are plotted in Fig. 5.

FIGURE 5.

Effects of cell properties on G-protein activation and receptor phosphorylation rates. (a) G-protein inactivation rate constant, k_i, varied from 0.1–10 s⁻¹. (b) Diffusion coefficient, D, varied from 10⁻¹⁰–10⁻¹¹ cm²/s. (c) Receptor kinase association rate constant, k_f-RK, varied from 100–1000 s⁻¹. Parameter values not mentioned are listed in Table 2.

As shown in Fig. 5 A, increasing the G-protein inactivation rate constant, k_i, increases a ligand's GARP value. The reason for this increase is that a larger k_i value results in a shorter G_βγ lifetime, which in turn limits the distance that a G_βγ can diffuse before becoming inactivated. Because G_βγ is responsible for recruiting receptor kinase to the membrane, a shorter G_βγ lifetime translates to a shorter receptor kinase lifetime and therefore less desensitization.

Changing the diffusion coefficient, D, of the proteins within the membrane also affects a ligand's GARP value as shown in Fig. 5 B. Physiologically, the diffusion coefficient could change due to changes in membrane lipid composition or changes in receptor localization—both of which would depend on the specific receptor type and cellular environment. Increasing the diffusion coefficient causes the system to be better mixed, resulting in both increased G-protein activation and receptor phosphorylation rates (data not shown). The G-protein activation rate increases because in a better-mixed system, local depletion zones like those shown in Fig. 3 play a less significant role. Similarly, the receptor phosphorylation rate increases because in a better-mixed system, a receptor kinase has access to more receptors. However, increasing the diffusion coefficient has a disproportionately larger effect on the receptor phosphorylation rate, resulting in a lower GARP value for most of the k_off values tested. The reason for this bias is that under low diffusion conditions, the mean time between receptor-G-protein collisions is long, reducing the probability that the two-step process of G-protein activation and subsequent receptor phosphorylation will complete before the ligand dissociates. In contrast, G-protein activation only depends on a single receptor-G-protein collision to take place and therefore is less sensitive to the effects of changing the diffusion coefficient. Interestingly, at high k_off values (∼10⁴ s⁻¹), the GARP value of the better-mixed system exceeds that of the less well-mixed system. This crossover may be explained by noting that at high diffusion coefficient values, the theoretical maximum number of G-proteins that can travel to a receptor to be activated is higher.

Finally, Fig. 5 C shows that decreasing the receptor kinase association rate constant, k_f-RK, increases a drug's GARP value. A smaller k_f-RK results in fewer receptor kinase proteins on the membrane and thus a reduced probability of receptor phosphorylation and a higher GARP value. Simulations also demonstrated that changing the receptor kinase dissociation rate constant, k_r-RK, reduces a drug's GARP value by the same mechanism (data not shown).

Physiologically, the value of k_f-RK could change with receptor localization or the total concentration of receptor kinase proteins near the membrane. Although the values of k_f-RK and k_r-RK are currently unknown, the simulation results indicate that changes in these parameters only scale the GARP profile, but do not change the qualitative behavior. Therefore, these findings reassure us that our choice of k_f-RK and k_r-RK values is not critical to the characteristic behavior of the system.

DISCUSSION

This modeling work was motivated by the observation that G-protein activation and receptor phosphorylation are sometimes but not always proportional (see Fig. 1). We speculated that this lack of correlation in some systems takes place because ligands differ not only in their efficacy (α in our model), but also in their dissociation rate constant, k_off.

The results in Figs. 4 and 5 show for the first time that changes in k_off can alter the receptor phosphorylation rate and hence alter the level of desensitization induced by the ligand. Furthermore, our results indicate that by varying α and k_off, the G-protein activation and receptor phosphorylation rates can be partially decoupled. These results have implications for our general understanding of receptor dynamics as well as for drug design. In the following sections we discuss the general structure of the relationship between activation and desensitization and provide two examples from the literature that demonstrate this behavior. Finally we discuss how our findings could be used to design drugs with tailored desensitization profiles.

Conserved relationship between GPCR activation and desensitization

Our simulation results demonstrate that GPCR activation and desensitization are related in a complicated, yet predictable, way. Therefore using our simulation results we attempted to discover a characteristic dynamic that describes the relationship between activation and desensitization in general terms. Because of the structure of the model, an analytical solution was not possible, forcing us to rely on patterns observed in the numerical results alone.

When the simulation results are replotted as activation rate vs. desensitization rate and only the k_off value of the drug is varied, we obtain a characteristic s-shaped activation vs. desensitization curve shown in Fig. 6 A. Increasing the α-value of a drug flattens and shifts the curve to the right, whereas changes to cellular parameters cause the curve to stretch or shift. However, in all cases tested, the underlying characteristic curve remains.

FIGURE 6.

Activation vs. desensitization simulation results for ligands with a variety of different dissociation rate constants (k_off) and efficacy (α) values. (a) Characteristic activation vs. desensitization response curves as affected by α and k_off. The response behavior for a range of α values can be divided into three regions: I, II, and III. (b) Activation and desensitization profiles for cellular conditions that favor signal localization (D = 10⁻¹¹ cm² s⁻¹; k_i = 10 s⁻¹; k_f-RK = 100 s⁻¹). (c) Activation and desensitization profile for cellular conditions that do not favor signal localization (D = 10⁻¹⁰ cm² s⁻¹; k_i = 0.1 s⁻¹; k_f-RK = 1000 s⁻¹). In both (b) and (c), dots represent individual ligand parameter value states and solid lines connect ligands of constant α (10⁵, 10⁶, and 10⁷) tested over k_off values ranging from 1 to 10000 s⁻¹. Note that the simulations do not predict that activation and desensitization are proportional.

The s-curve can be divided into three distinct regimes, each corresponding to a different range of k_off values. In region I, k_off values are low, corresponding to ligands with a long bound lifetime on a single receptor as is illustrated in Fig. 3 A. In this region, activation and desensitization both increase with increasing k_off. Physically, ligands in region I have a sufficiently long ligand-receptor half-life that the G-protein activation rate comes to steady state and nearly every ligand-bound receptor becomes phosphorylated before the ligand dissociates. At the opposite extreme is region III, corresponding to ligands with large k_off values. For ligands in this region, the ligand-receptor half-life is sufficiently short that diffusion-limited G_βγ enrichment zones surrounding the receptor are minimized as illustrated in Fig. 3 C. Therefore, region III ligands tend to cause less phosphorylation per receptor, but visit more receptors and activate overall more G-proteins. As a result, the large k_off value of ligands in region III tends to cause an increase in both G-protein activation and phosphorylation as was discussed earlier in the results section.

Most interestingly, ligands in region II have an intermediate k_off value, which allows them to cause disproportionately more G-protein activation than receptor phosphorylation. Physically, ligands in this region are able to bind for a sufficiently long time to activate nearly all of the local G-proteins surrounding the receptor (Fig. 3 B), but often not long enough to phosphorylate the receptor. By sitting at the tipping point in k_off between G-protein activation and receptor phosphorylation, the drug is able to maximize its signal although minimizing its desensitization. Note that this same tipping point can be observed in Fig. 4 C at a k_off value of 2500 s⁻¹. The location of this tipping point in k_off varies as a function of the ligand conformational selectivity factor, α, and the cell specific parameters as was described in the results section.

To explore how changes in α and cell-specific parameters affect the characteristic relationship between activation and desensitization, additional simulations were run using a variety of ligands (black dots) under two different cellular conditions (Fig. 6, B and C). Ligands of constant α are linked by a solid line.

When diffusion is slow and the half-life of signaling species is short, the k_off value of a ligand has a greater ability to differentially regulate activation and desensitization, as is shown in Fig. 6 B. Under these cellular conditions, receptor signaling events are spatially isolated. This isolation, in turn, makes the cell permissive to ligand switching effects like the behavior illustrated in Fig. 3.

In contrast, when diffusion is fast and the half-life of signaling species is long, the k_off value of a ligand regulates both activation and desensitization in a similar way (Fig. 6 C). These cellular conditions tend to distribute signaling events over many receptors, thereby reducing the ability of ligand switching to exploit the delay between G-protein activation and receptor kinase recruitment. As a result, these cellular conditions reduce the ability of ligand switching to differentially regulate activation and desensitization.

Under both cellular conditions, increasing the α-value of a ligand flattened and shifted the curve to the right as is shown in Fig. 6, B and C. In some cases only part of the curve is present in the range of k_off values tested. For example, in Fig. 6 C, at low α-values only region II is represented. In other cases, the curve is sufficiently compressed that region II vanishes completely and only regions I and III are present (Fig. 6 C, right two lines). Similarly, in Fig. 6 B, the left-most curve shows only regions II and III, but has lost region I.

The trends in the model predictions made in Fig. 6 are in qualitative agreement with the experimental results in Fig. 1. Experimentally, it has been found that G-protein activation and desensitization are not simply correlated for at least two receptor systems (see Fig. 1, B and C). Similarly, our simulations show that only under limited conditions would one expect to find a simple relationship between activation and desensitization. For example, imagine testing a small number of ligands from Fig. 6 B, each with its own α and k_off values, and plotting their activation vs. desensitization profiles together as was done in Fig. 1. The resulting plot may show a general correlation between activation and desensitization, but this correlation would be poor and would likely include examples of drugs that exhibit disproportionately more activation than desensitization. However, underlying the simulation results and likely the experimental results, a family of nonlinear s-curves that precisely describes how activation and desensitization respond to α and k_off is illustrated in Fig. 6 A. Therefore in many cases the presence of these s-curves prevents us from drawing a simple linear relationship between signaling and desensitization, from both theoretical and experimental data.

Inside-out control of desensitization via k_i

An intriguing possibility is that by regulating its G-protein inactivation rate constant, k_i, the cell itself could dynamically alter the GARP value of a ligand as demonstrated by the modeling results in Fig. 5 A. By changing its k_i value, the cell could exert a form of inside-out control on its signaling environment.

One way the cell could vary its k_i value is by regulating the activity of regulators of G-protein signaling (RGS) proteins inside the cell. RGS proteins bind directly to G_α-GTP and act as GTPase-activating proteins to attenuate GPCR signaling, thereby increasing the apparent k_i value inside the cell (Neubig and Siderovski, 2002). Changes in RGS expression and localization have been detected for a number of receptor systems. For example, work with the endothelin-1 receptor has indicated that RGS4 and RGS16 are upregulated in response to GPCR signaling (Patten et al., 2002). Similarly, in yeast the GPCR-mediated pheromone response is mediated by the recruitment of RGS8 to the cell membrane from the cytosol (Saitoh et al., 2001). These data suggest that the cell does regulate its own k_i value via RGS proteins in response to GPCR signaling.

By dynamically regulating the RGS concentration, the cell would not only attenuate the short-term signal caused by a ligand, but according to the simulation results in Fig. 5 A, would also cause a disproportionately large change in the receptor phosphorylation rate caused by the ligand. This modeling prediction has been observed experimentally. For example, measurements of membrane depolarization in response to GPCR signaling have shown that the expression of RGS4 causes little change in the maximal signal, but can significantly reduce ligand-mediated desensitization (Chuang et al., 1998). This change in signaling and desensitization corresponds to an increased apparent GARP value upon RGS expression, which is in agreement with the simulation results in Fig. 5 A. Similar examples of differential regulation of GPCR signaling and desensitization by RGS proteins have been demonstrated for the μ-opioid receptor system (Garzon et al., 2001).

By differentially regulating the GPCR signaling and desensitization via RGS proteins, the cell could control its dynamic signaling range via an inside-out mechanism. In the classic view of GPCR signaling, the ligand alone governs desensitization whereas the cell is a passive detector. However, by regulating the activity of RGS proteins, the cell may be able to affect how it detects a ligand, perhaps changing a highly desensitizing ligand into a ligand that induces little desensitization.

μ-Opioid receptor and the morphine paradox

G-protein signaling and receptor desensitization have been well studied in the μ-opioid receptor system in an effort to develop better pain management medications. Of particular relevance to this work, the μ-opioid agonist morphine is unique in that it is able to elicit a signal and yet causes nearly no receptor phosphorylation (Yu et al., 1997).

According to our simulations, morphine's paradoxical ability to signal with minimal desensitization is possible if morphine is in region II of Fig. 6 A. In this state, morphine would bind long enough to activate many G-proteins but not long enough to cause phosphorylation of the receptor. In agreement with this prediction, morphine is known to bind weakly to the receptor (Zhang et al., 1998)—thus possibly accounting for its disproportionately low receptor phosphorylation rate.

Available data on other ligands to the μ-opioid receptor are also consistent with the model predictions. Data for three such ligands are shown in Table 3, along with data on morphine. All of these ligands exhibit the general trend that at low k_off values, signaling and desensitization are both relatively high, whereas at high k_off values, signaling is favored over desensitization. This finding is in agreement with the s-curve behavior in which drugs with a low k_off value correspond to region I drugs, whereas drugs with an intermediate to high k_off value correspond to region II drugs. It is possible that region III drugs do not appear in this assay because either the diffusion coefficient in this system is large or that the drug's affinity for the receptor is too low to be a useful drug.

TABLE 3.

Relationship between activation, desensitization, and ligand dissociation rate for four common ligands to the μ-opioid receptor

Ligand	G-protein activation	Ligand dissociation rate	Receptor desensitization	References
morphine	intermediate	fast	low	Blake et al., 1997; Rothman et al., 1995; Zhang et al., 1998
etorphine	high	slow	high	Blane et al., 1967; Rothman et al., 1995; Zhang et al., 1998
buprenorphine	intermediate	slow	high	Blake et al., 1997; Rothman et al., 1995
DAMGO	high	fast	intermediate	Scheibe et al., 1984; Tolkovsky, 1982; Yu et al., 1997

Table modified from Riccobene, 1999.

Clinical work with the μ-opioid receptor by Shen and Crain (1997) has demonstrated that coadministration of low doses of a neutral antagonist, such as naloxone or naltrexone, along with an agonist can cause the agonist to signal for a longer period of time before becoming desensitized. By blocking receptors with the neutral antagonist, Shen and Crain (1997) have essentially reduced the receptor density in the system without affecting the agonist dissociation rate. This reduction in receptor density would be expected to cause an increased isolation of signaling events, similar to the cellular conditions presented in Fig. 6 B. The qualitative result as predicted by the model is that adding a neutral antagonist should distort the s-curve–type behavior of the signal vs. desensitization profile, possibly moving the activity of the agonist to a less desensitizing region.

Impact for drug design

To include desensitization as a design criteria will require a fundamental change in the way drug designers view their goal. Historically drug design has focused on optimizing a drug's ability to signal and its potency, viewing desensitization as an unavoidable side effect. In contrast to this view, our simulation results indicate that desensitization can be, at least in part, decoupled from signaling and tailored for specific therapeutic applications. As a rule of thumb, drugs with a lower efficacy (lower α) and intermediate dissociation rate constant (k_off) will cause a disproportionately less desensitization than activation. This combination of efficacy and dissociation may in part account for why drugs such as morphine cause such small levels of desensitization although still causing an appreciable signal.

However, changing a drug's desensitization profile comes at a cost to both the drug's absolute signaling ability and its potency. For example, if a drug has a lower affinity for its receptor then it must be given at higher doses, possibly leading to toxic side effects. Drug designers have historically circumvented many toxicity issues by developing drugs that bind tightly to the receptor, thereby permitting extremely low effective dosages. Although this approach resulted in less toxicity, it may have also inadvertently optimized for drugs that cause maximal desensitization. Similarly, by reducing the efficacy of a drug (reduced α), one also reduces the maximal ability of the drug to signal. As shown in Fig. 4, the drugs that have the best GARP profile (Fig. 4 C) mount a modest absolute response (Fig. 4 A).

Decoupling desensitization and activation opens the intriguing possibility of designing drugs that primarily act by desensitizing the receptor, with their signaling ability playing a secondary role. These drugs could find use in reducing the expression levels of certain receptors that are elevated after prolonged exposure to antagonists or inverse agonists. For example, long-term treatment of heart disease with β₂-adrenergic receptor antagonists results in upregulation of the receptor, resulting in hypersensitivity to endogenous ligands to the receptor (Strauer, 1990). Similarly, long-term treatment of schizophrenia with antipsychotics such as haloperidol has been shown to cause upregulation of dopamine D₂ receptors and an associated hypersensitivity to dopamine (Silvestri et al., 2000). The simulation results presented here suggest that low doses of drugs with a low dissociation rate constant and high efficacy would cause disproportionately more desensitization than G-protein activation. Using these desensitization drugs, it may be possible to safely control the expression level of certain receptor types in the body.

Together our results suggest an exciting new direction in pharmacology in which drug-induced signaling and desensitization may be controlled independently by changing drug properties.