Effect of External Magnesium and Calcium on Human Connexin46 Hemichannels

Abstract

One of the most striking features of hemi-gap-junctional channels is that they are dramatically modulated by extracellular divalent cations. In this study, we characterized the effects of external divalent cations and voltage on macroscopic human connexin46 (hCx46) hemi-gap-junctional currents using the two-electrode voltage-clamp technique. Increasing extracellular magnesium resulted in a shift of the voltage dependence of activation to more positive potentials, a decrease in the maximum conductance, an acceleration of deactivation, and a slowing of activation. Hyperpolarizing the membrane potential could mimic the effect of raising external magnesium on the activation kinetics and maximum conductance. These results could be interpreted in terms of a sequential model of channel activation with two independent divalent cation binding sites. This model could also explain the effects of external calcium on hCx46 hemichannels. However, the apparent binding affinities for calcium were significantly higher than for magnesium. In addition, we identified a mutation in the first extracellular domain of hCx46 (hCx46*N63S) that resulted in hemichannels that showed increased sensitivity to magnesium blockade.

INTRODUCTION

Gap junctional channels are formed from two hemichannels or connexons (one contributed by each cell of the pair). Each connexon is, in turn, a multimeric complex composed of six protein subunits known as connexins. At least 19 different connexins have been identified in rodents (Willecke et al., 2002).

There is substantial biochemical, morphological, and electrophysiological evidence that suggests that gap junctional channel proteins exist as freely floating connexons or hemichannels in the nonjunctional plasma membrane before their assembly into gap junctional channels. It was originally thought that these connexons always remain in the closed state. However, DeVries and Schwartz (1992) showed that solitary horizontal cells from the catfish retina expressed a novel dopamine-sensitive membrane current that was present only when the extracellular calcium concentration was reduced. These channels showed many of the properties expected for hemichannels, including poor selectivity for monovalent cations, permeability to the anionic dye, lucifer yellow, and large unitary conductances. Further evidence in support of the hypothesis that this nonjunctional current was due to open hemichannels came from oocyte expression experiments which showed that several connexins were able to form functional hemi-gap-junctional channels in oocytes that opened on depolarization and could be blocked by extracellular calcium or intracellular acidification (Paul et al., 1991; Trexler et al., 1996; Ebihara, 1996; Ebihara et al., 1999; Beahm and Hall, 2002; White et al., 1999; Pfahnl et al., 1997; Pfahnl and Dahl, 1999).

There have been a number of other observations that suggest that connexons exist in the nonjunctional plasma membrane and can open under certain conditions. Li et al. (1996) showed that mammalian cells expressing Cx43 took up 5(6)-carboxyfluorescein when the extracellular calcium concentration was reduced and that this dye uptake exhibited properties similar to those of gap junctional channels. Nonjunctional currents arising from hemichannels have also been recorded in mammalian cell lines transfected with Cx45, Cx30, Cx46, and Cx50 in calcium-free bath solutions using the whole cell patch clamp technique (Valiunas, 2002; Valiunas and Weingart, 2000). John et al. (1999) reported that isolated cardiac myocytes endogenously express connexin hemichannels that are gated by metabolic inhibition. Quist et al. (2000) reported that hemichannels were involved in calcium-dependent isosmotic volume regulation in a variety of mammalian cells expressing connexins.

One of the most striking features of hemi-gap-junctional channels is that they are dramatically modulated by extracellular divalent cations. It has been previously shown that removal of external calcium caused a marked increase in the amplitude of the rCx46 hemi-gap-junctional current, shifted the steady-state activation curve to more negative potentials, and altered the kinetics of activation and deactivation (Ebihara and Steiner, 1993). At the single channel level, the main effect of reducing external calcium was to increase the probability of channel opening (Pfahnl and Dahl, 1999). The actions of calcium were voltage dependent suggesting that calcium was binding to a site within the pore.

Recently, Muller et al. (2002) imaged connexon structure at molecular resolution (<2 A vertical resolution and <10 A lateral resolution) using atomic force microscopy in aqueous solution in the presence and absence of calcium. Images of layers of single connexons showed a reversible reduction in the diameter of the external pore during incubation with calcium. The time course of this conformational change was extremely slow. This phenomenon appeared to be distinct from the effect of calcium on intact gap junctional channels.

In the experiments described here, we used macroscopic current measurements to examine the effects of extracellular magnesium and calcium on gating of hCx46 hemi-gap-channel currents expressed in Xenopus oocytes. Our results suggest that external divalent cations modulate the first step in the deactivation process and early gating transitions in the activation process. The kinetics of the early gating transitions resembles that of calcium-sensitive conformational change imaged using atomic force microscopy. The role of asparagine 63 in [Mg²⁺]_o modification of hemichannel gating is also explored.

METHODS

cDNA/cRNA preparation

The cDNAs for wild-type hCx46 and hCx46N63S were subcloned into the RNA expression vector, SP64TII, as previously described (Pal et al., 2000). Mutagenesis of the amino acids at position 63 of hCx46 was carried out by using the QuickChange Site-directed Mutagenesis kit (Stratagene, La Jolla, CA). The nucleotide sequence of mutant N63Q was verified by sequencing the entire coding region of the corresponding cDNA (DNA sequencing facility, Iowa State University, Ames, IA). The plasmids were linearized with SalI and capped RNAs were synthesized using the mMessage mMachine SP6 in vitro transcription kit according to the manufacturer's instructions (Ambion, Austin, TX). The amount of RNA was quantitated by measuring the absorbance at 260 nm. The cRNA for ROMK2 was a generous gift of Dr. Henry Sackin (FUHS, North Chicago, IL).

Female Xenopus laevis frogs were anesthetized and a partial ovarectomy performed. Oocytes were rinsed in zero Ca²⁺ modified Barth's solution (88 mM NaCl, 1 mM KCl, 2.4 mM NaHCO₃, 15 mM Hepes, 0.82 mM MgSO₄, and 50 μg/ml gentamicin at pH 7.4) before treatment with 10 mg/ml type IA collagenase (Sigma, St. Louis, MO) for 20 min. Stage V and VI oocytes were then manually defolliculated and coinjected with 46 nl of connexin cRNA and antisense oligonucleotide to endogenous Cx38 (AS-Cx38) to eliminate endogenous hemichannel currents (Ebihara, 1996). Oocytes were incubated in modified Barth's solution (MBS) containing 0.7 mM Ca²⁺, 0.8 mM Mg²⁺, and 1 mM Ba²⁺ for up to two days before examination.

The two microelectrode voltage clamp technique was used to measure hemi-gap-junctional currents in single oocytes using a Geneclamp 500 amplifier (Axon Instruments, Union City, CA) as the voltage clamp amplifier. Bath error potentials were minimized by actively clamping the bath to zero. The current and voltage microelectrodes were filled with 3 M KCl (pH 7.8) and had resistances of 0.2–2 M. The current signal was filtered at 100 or 50 Hz using a four-pole low pass Bessel filter and sampled at 0.2–1 kHz. Data acquisition and analysis were performed using a personal computer running Pclamp Version 6 (Axon Instruments). All recordings were performed at room temperature (20–22°C). The standard bath solution contained zero Ca²⁺ modified Barth's solution to which different concentrations of MgCl₂ or CaCl₂ + EGTA were added. Calcium concentrations were calculated using the Eqcal software package (Biosoft, Cambridge, UK). To study the effect of changing external magnesium or calcium, solutions containing successively higher divalent cation concentrations were perfused into the 2-ml chamber by gravity flow. Complete solution change (∼10 bath volumes) was achieved within ∼2–5 min. The voltage-clamp protocol was applied to the oocyte starting ∼15–20 min after each solution change. The oocyte was held at a holding potential of −10 mV between solution changes unless otherwise specified. To study the kinetics of calcium and magnesium block, we used an oocyte perfusion chamber (Bioscience Tools, Brookline, MA) that had a working volume of ∼20 μl which allowed complete solution change (∼10 vol) to be achieved within 30 s. Delays attributable to diffusion and unstirred layers around the oocyte were estimated from the time course of the change in resting potential of oocytes expressing the inwardly potassium channel, ROMK2, after a change in [K⁺]_o. Elevation of [K⁺]_o from 1 to 10 mM resulted in a 50-mV depolarization of the oocyte in less than 25 s.

RESULTS

Effect of [Mg²⁺]_o on deactivation kinetics and steady-state activation

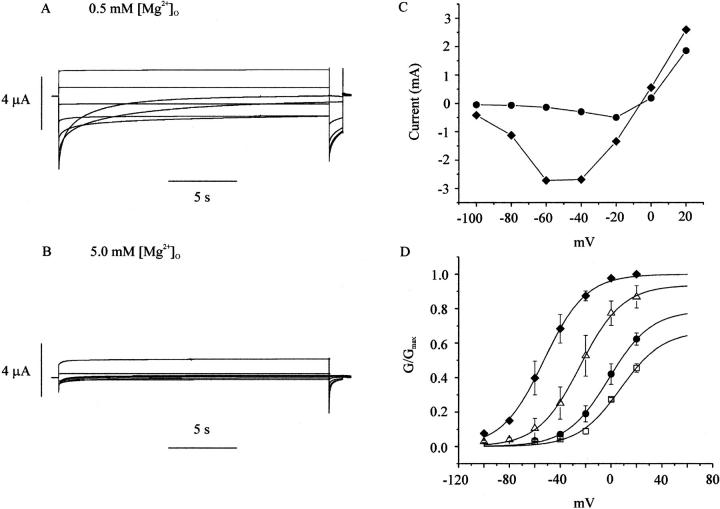
Human connexin46 (hCx46) hemi-gap-junctional currents were recorded during a series of depolarizing and hyperpolarizing pulses from a holding potential of −10 mV in the presence of various concentrations of external magnesium. We have focused on magnesium because Mg²⁺ does not activate endogenous calcium-activated chloride channels and blocks the channel at millimolar concentrations. In the presence of 0.5 mM [Mg²⁺]_o, the current was almost fully activated at −10 mV. Hyperpolarizing pulses elicited a large inward current that decayed with time (reflecting deactivation) as illustrated in Fig. 1 A. The rate of decay increased with increasing hyperpolarizing steps. Two time constants were usually needed to fit the time course of channel closing. When [Mg²⁺]_o was increased to 5 mM, both the rate and extent of deactivation increased (Fig. 1 B). The effect of Mg²⁺ was voltage dependent, because the effect became more prominent at more negative potentials. In external solutions containing no added divalent cations, voltage dependent gating disappeared and the current remained fully activated over the voltage range between 20 mV and −100 mV (data not shown).

FIGURE 1.

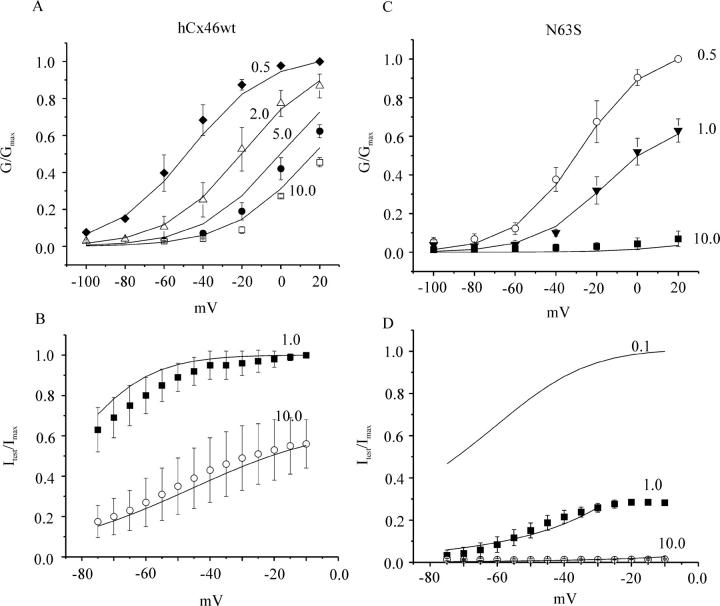
Effect of extracellular magnesium on human Cx46 hemichannel currents. Representative hemichannel currents recorded from a wild-type hCx46 cRNA-injected oocyte in zero calcium MBS containing 0.5 mM [Mg²⁺]_o (A) or 5.0 mM [Mg²⁺]_o (B). The cell was held close to the hemichannel equilibrium potential (−10 mV) between pulse sequences to minimize holding currents. A 20-s conditioning voltage clamp pulse was applied to voltages between 20 and −100 mV in decrements of 20 mV followed by a test pulse to −80 mV. Data were corrected for a linear leakage component that was estimated from the I-V relationship between −80 and −100 mV in the presence of 10 mM [Mg²⁺]_o. (C) Steady-state I-V curves at different magnesium concentrations: 0.5 mM (closed diamonds); 5.0 mM (solid circles). The steady-state current was measured at the end of the 20-s conditioning pulse. (D) Normalized G-V curves at different magnesium concentrations: 0.5 mM (closed diamonds); 2.0 mM (open triangles); 5.0 mM (solid circles); 10.0 mM (open squares). Normalized conductance (G/G_max) was determined at each potential by measuring the initial amplitude of the tail current during the test pulse to −80 mV and dividing it by the maximum value of the tail current obtained after a depolarization to +20 mV in the presence of 0.5 mM [Mg²⁺]_o. The initial value of the tail current was estimated by fitting the tail current to the sum of two exponentials and extrapolating back to zero time. Symbols and bars indicate means ± SE. N = 4. The solid lines in D are fits to the Boltzmann equation, y = G(V_sat)/G_max/(1 + exp(−k × (V−V_1/2))) with k constrained to 0.06. For 0.5 mM [Mg²⁺]_o, V_1/2 = −52.9 mV, G(V_sat)/G_max = 1.0; for 2 mM [Mg²⁺]_o, V_1/2 =−24.3 mV, G(V_sat)/G_max = .937; for 5 mM [Mg²⁺]_o, V_1/2 = −1.69 mV, G(V_sat)/G_max = 0.79; for 10 mM [Mg²⁺]_o, V_1/2 = 7.3 mV, G(V_sat)/G_max = 0.67.

Fig. 1 C shows the effect of magnesium on the isochronal I-V relationship determined by measuring the current at the end of a 20-s pulse to different potentials. This pulse length was chosen because it was long enough to allow the current to reach steady state at most external magnesium concentrations. Increasing [Mg²⁺]_o reduced the amplitude of the quasisteady-state current and shifted the I-V curve to more positive potentials. The effect of magnesium on the conductance-voltage (G-V) curve was determined by repolarizing the membrane potential to −80 mV at the end of the 20-s test pulse and plotting the initial amplitude of I_tail at −80 mV as a function of test potential. The main effect of increasing magnesium was to shift the G-V curve to more positive potentials. Increasing magnesium also caused a small decrease in the estimated value of G/G_max at saturating potentials (Fig. 1 D). The effects of external magnesium on the hemichannel current are reminiscent of the effects of internal magnesium on the inwardly rectifying potassium current, suggesting that external magnesium binds to a site within the pore and occludes the conduction pathway. As would be expected in such a case, large negative potentials cause an increase in the local concentrations of external cations and lead to channel blockade, whereas depolarizations cause relief of block by the permeating cation.

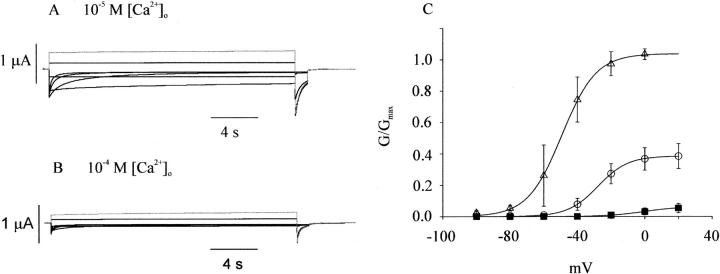
The effect of external calcium on the hCx46 hemi-gap-junctional current was also examined using the same experimental protocols in solutions containing nominally zero magnesium. Fig. 2 shows the voltage-dependent behavior of wild-type hCx46 at two different calcium concentrations. The effect of calcium on the hCx46 hemi-gap-junctional current was similar to that of magnesium. Increasing calcium slowed the rate of activation, accelerated the rate of deactivation, shifted the G-V curve progressively to more positive potentials, and decreased the maximum conductance. However, the effect of calcium appeared to be more potent than that of magnesium; the V_1/2 for the G-V curve in 1 mM Ca²⁺ was similar to that in 10 mM Mg²⁺. In addition, G_max was much more strongly inhibited by calcium than magnesium.

FIGURE 2.

Effect of extracellular calcium on human Cx46 hemichannel currents. Representative hemichannel currents recorded from a wild-type hCx46 cRNA-injected oocyte in solutions containing zero added magnesium and .01 mM [Ca²⁺]_o (A) or .1 mM [Ca²⁺]_o (B). The cell was held at the hemichannel equilibrium potential (−10 mV) between pulse sequences to minimize holding currents. A 20-s conditioning voltage clamp pulse was applied to voltages between 20 and −100 mV followed by a test pulse to −80 mV. Data were corrected for a linear leakage component. (C) Normalized G-V curves at different calcium concentrations: 0.01 mM (open triangles); 0.1 mM (open circles); 1.0 mM (solid square). Normalized conductance (G/G_max) was determined at each potential by measuring the initial amplitude of the tail current during the test pulse to −80 mV and dividing it by the maximum value of the tail current obtained after a depolarization to +20 mV in the presence of .01 mM [Ca²⁺]_o. Symbols and bars indicate means ± SE. N = 3–6 experiments. The solid lines in C are fits to the Boltzmann equation, y = G(V_sat)/G_max/(1 + exp(−k × (V − V_1/2))). For 0.01 mM [Ca²⁺]_o, G(V_sat)/G_max = 1.02, V_1/2 = −50 mV, k = 0.102; for 0.1 mM [Ca²⁺]_o, G(V_sat)/G_max = 0.385, V_1/2 = −27.7, k = 0.112; for 1.0 mM [Ca²⁺]_o, G(V_sat)/G_max = 0.06, V_1/2 = −0.9 mV, k = 0.096.

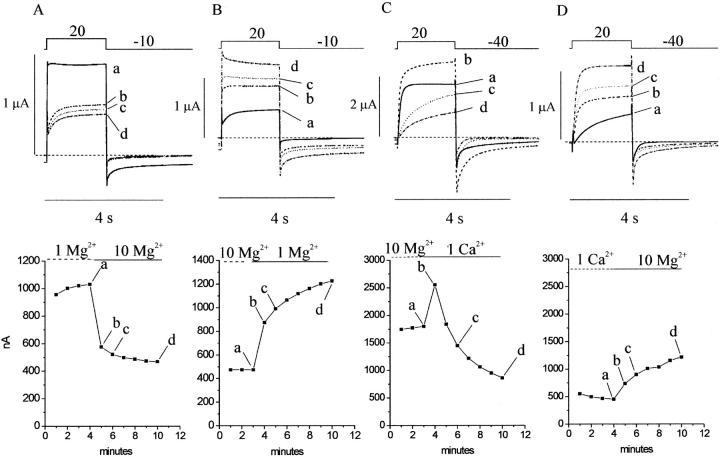
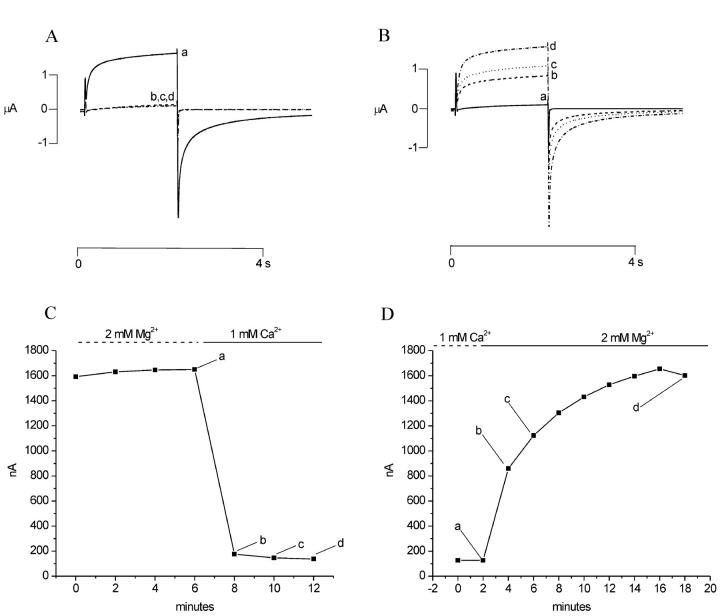
The time course of block and recovery from block of the hemichannel current by external magnesium is shown in Fig. 3, A and B. In this experiment, the hCx46 cRNA-injected oocyte was held at −10 mV and subjected to continuous perfusion. The amplitude of the hemichannel current was monitored using brief depolarizing pulses to 20 mV every 60 s. After allowing the current to stabilize in an extracellular solution containing 1 mM Mg²⁺, the cell was superfused with extracellular solution containing 10 mM Mg²⁺ beginning at time = 4 min, followed by perfusion of solution containing 1 mM Mg²⁺. The current at the end of the test pulse was plotted as a function of perfusion time. Application of 10 mM Mg²⁺ caused a rapid decrease in the amplitude of the current (due to a shift in the G-V curve to the right) followed by a more gradual reduction. Reperfusion with solution containing 1 mM Mg²⁺, resulted in a rapid increase in current (due to a shift in the G-V curve to the left) followed by a slower increase. Fig. 3 C shows an example of an experiment in which a hCx46 cRNA-injected oocyte was initially superfused with a solution containing 10 mM Mg²⁺ and then the solution was switched to one containing 1.0 mM Ca²⁺ at time = 3 min. Application of 1.0 mM Ca²⁺ caused a slowing of deactivation and a rapid increase in the amplitude of the hemichannel current (due to a shift in the G-V curve to the left) followed by a more gradual reduction in the current. This reduction in amplitude was associated with a progressive slowing of the activation kinetics. When the cell was reperfused with an external solution containing 10 mM Mg²⁺, the time course of activation sped up and the amplitude of the current slowly recovered to its original value before application of 1.0 mM Ca²⁺ (Fig. 3 D). Similar results were obtained in five other experiments. One explanation for the biphasic time course of the calcium effect is that there are at least two distinct binding sites for divalent cations that have different relative affinities for calcium and magnesium and modulate different steps in the activation process.

FIGURE 3.

Time course of block and recovery from block of hemichannel currents in two hCx46 cRNA-injected oocytes by extracellular magnesium (A and B) and calcium (C and D). (A) Upper panel shows a sequence of traces recorded upon depolarization to +20 mV from a holding potential of −10 mV at various times during perfusion with 1 mM [Mg²⁺]_o (a) and after switching to 10 mM [Mg²⁺]_o (b,c,d). Lower panel shows the time course of inhibition of the hemichannel current after application of 10 mM [Mg²⁺]_o; labels a–d indicate the records shown in A. (B) Upper panel shows sequence of traces recorded in same cell during perfusion with 10 mM [Mg²⁺]_o (a) and after return to 1 mM [Mg²⁺]_o (b,c,d). Lower panel shows the time course of recovery of the hemichannel current. (C) Upper panel shows sequence of traces recorded in a different cell during perfusion with 10 mM [Mg²⁺]_o and after switching to 1 mM [Ca²⁺]_o. Lower panel shows time course of inhibition of the hemichannel current after application of calcium. (D) Upper panel shows sequence of traces recorded in the same cell in the presence of 1 mM [Ca²⁺]_o (a) and after reperfusion with 10 mM [Mg²⁺]_o (b,c,d). Lower panel shows the time course of recover of the hemichannel current. Data corrected for a linear leakage current. Dashed line indicates zero current level.

Effects of holding potential on activation gating

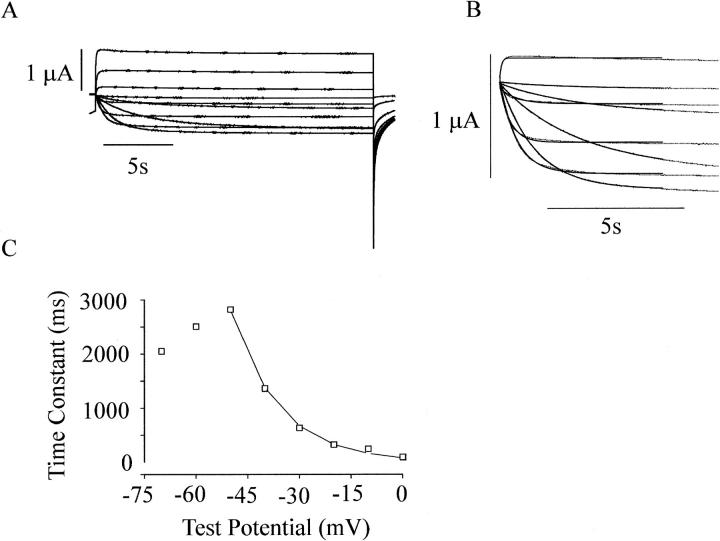
Fig. 4 A shows membrane currents recorded from an oocyte injected with wild-type hCx46 cRNA in response to a series of depolarizing voltage clamp steps from −70 to 30 mV in 10-mV increments from a holding potential of −80 mV. The channels rarely opened at −80 mV in the presence of 1 mM external Mg²⁺. Upon depolarization, these currents activate with a nearly exponential time course. This can be more clearly seen in Fig. 4 B which shows a subset of these currents on an expanded time scale fit to a single exponential function. The time constants of activation are plotted as a function of membrane potential in Fig. 4 C. The time constant of activation was largest at −50 mV and decreased at more positive and negative potentials indicating that both the forward and backward rate constants are voltage dependent.

FIGURE 4.

Time course of activation of hCx46 hemi-gap-junctional currents in the presence of 1.0 mM [Mg²⁺]_o. (A) Currents were elicited with 20-s voltage clamp steps to test potentials ranging from −80 to +20 mV in 10-mV increments. Holding potential = −80 mV. Data corrected for a linear leakage component. (B) A subset of the traces shown in (A) have been expanded (−70 mV–0 mV), and their activation time courses fitted with a single exponential function (dotted line). (C) Time constant of activation plotted as a function of test potential.

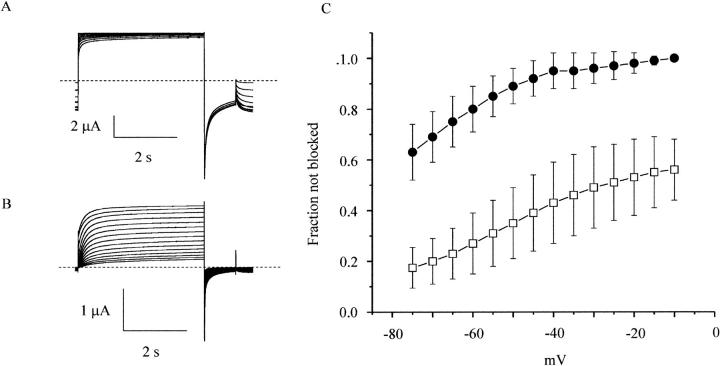
Previous studies have shown that the kinetics of activation of rat Cx46 hemichannels depends on both external divalent cations and holding potential (Ebihara and Steiner, 1993). In the present study, we used a sequential protocol to study the effect of holding potential on hCx46 hemichannels over a large range of voltages as illustrated in Fig. 5, A and B. In this protocol, the cells were held at various holding potentials starting at −10 mV for 116 s followed by a 4-s test pulse to 20 mV. Then the holding potential was decremented by 5 mV and the pulse protocol was repeated. The current at the end of the test pulse (I_test) was normalized with respect to the maximum value of I_test and plotted as a function of holding potential in Fig. 5 C. The main effect of hyperpolarization was to reduce I_test without having a significant effect on fast activation kinetics. This effect was enhanced in the presence of elevated [Mg²⁺]_o. The voltage and magnesium dependence of the steady-state availability curve resembles that of the G-V curve suggesting that this process might be related to channel gating. In particular, it seems plausible that the voltage dependence was due to magnesium binding preferentially to closed channels and stabilizing them in the closed state.

FIGURE 5.

Effect of holding potential on activation. The effect of holding potential on wild-type hCx46 hemichannel currents was measured using a sequential pulse protocol. In this protocol, the cell was held at various holding potentials, starting at −10 mV for 116 s followed by a 4-s test pulse to 20 mV. Then the holding potential was decremented by 5 mV and the pulse protocol was repeated. Representative families of current traces recorded at holding potentials between −10 and −75 mV in the presence of 1 mM (A) or 10 mM [Mg²⁺]_o (B). Data corrected for a linear leakage current. Dashed line indicates zero current level. (C) Steady-state hemichannel availability curves measured at different magnesium concentrations: 1.0 mM (solid circles); 10.0 mM (open squares). The fraction of hemichannels available at each holding potential was determined by dividing the current measured at the end of the test pulse by the maximum value of the current obtained in the presence of 1.0 mM [Mg²⁺]_o. Symbols and bars indicate means ± SE. N = 4.

To test whether divalent cations can bind directly to closed channels and exert an inhibitory effect, the oocyte was superfused with various concentrations of [Mg²⁺]_o or [Ca²⁺]_o under conditions in which most of the hemichannels were mostly closed (i.e., at −80 mV in the presence of 2 mM [Mg²⁺]_o). Fig. 6 shows an example of hemichannel currents recorded during 4-s test pulses to 20 mV immediately before and after application of 1 mM [Ca²⁺]_o. The amplitude of the current evoked by the first test pulse after application of calcium was markedly reduced compared to control currents in 2 mM [Mg²⁺]_o and was associated with a slowing of activation. Subsequent current pulses showed little or no further reduction in the size of the current. This shows that divalent cations can directly bind to the closed configuration of the channel and stabilize the channel in the closed/blocked state.

FIGURE 6.

Closed channel block of hCx46 hemichannel current by external calcium. hCx46 cRNA-injected oocytes were held at −80 mV in the presence of calcium-free MBS containing 2 mM [Mg²⁺]₀ to close the hemichannels. Then 1 mM [Ca²⁺]_o was applied to the oocyte. (A) Upper panel shows superimposed current records recorded sequentially during 4-s test pulses to 20 mV from a holding potential of −80 mV just before (a) and after perfusion with 1 mM [Ca²⁺]_o (b,c,d). Lower panel shows I_test amplitude plotted as a function of time; labels a–d indicate the traces shown in A. (B) Upper panel shows superimposed current traces recorded sequentially in the same cell following return to calcium-free MBS containing 2 mM [Mg²⁺]_o. Lower panel shows the time course of recovery of the hemichannel to its original state; labels a–d indicate the traces shown in B.

Role of asparagine 63 in [Mg²⁺]_o modification of hemichannel gating

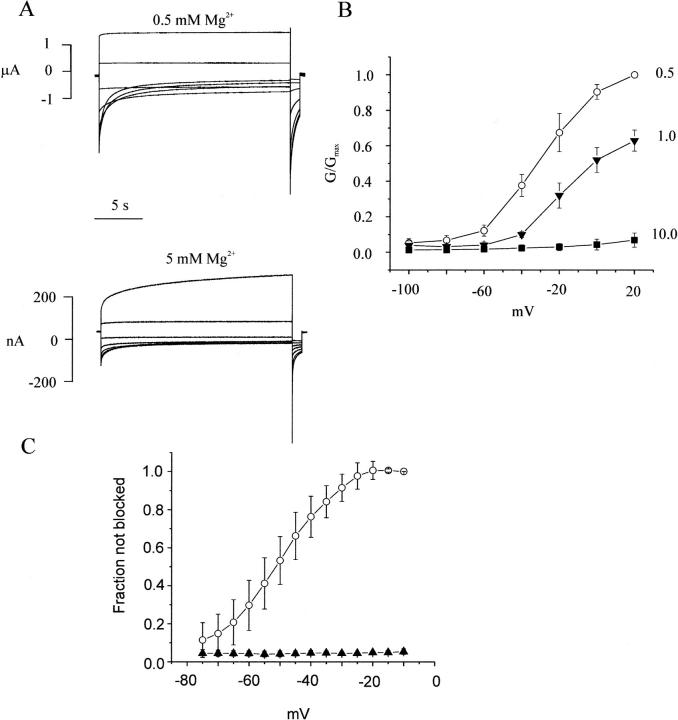
While studying human Cx46 mutations associated with congenital cataracts, we previously found that one of these mutations (an asparagine–serine substitution at position 63 in the first extracellular domain) formed hemi-gap-junctional currents whose amplitudes were much smaller than those observed in oocytes injected with similar amounts of wild-type hCx46 cRNA under standard recording conditions (i.e., in the presence of 0.7 mM [Ca²⁺]_o and 0.8 mM [Mg²⁺]_o) (Pal et al., 2000). However, when the concentration of divalent cations was reduced, the magnitude of this current increased dramatically suggesting that the N63S mutation increased the external divalent cation sensitivity of hCx46 hemichannels. To further explore this phenomenon, we examined the effect of external magnesium on macroscopic N63S currents. Fig. 7 shows typical families of current traces, mean steady-state G-V curves and steady-state channel availability curves recorded from N63S cRNA-injected oocytes in the presence of various concentrations of external magnesium. The effects of magnesium on N63S hemichannel currents were similar to its effects on wild-type currents. Increasing [Mg²⁺]_o accelerated the time course of deactivation, shifted the G-V curve to more depolarized potentials and decreased the maximum conductance. However, G_max was much more strongly inhibited by magnesium in oocytes expressing N63S. The effect of holding potential on the N63S mutant was examined using the sequential pulse protocol previously described in Fig. 4. The mutant current was almost completely inhibited by 1 mM [Mg²⁺]_o at hyperpolarized holding potentials (Fig. 7 C). Increasing [Mg²⁺]_o to 10 mM totally suppressed the current at all holding potentials. These results suggest that one of the main effects of the N63S mutation is to increase the binding affinity of the second divalent cation binding site for magnesium and thereby stabilize the mutant channel in the closed/blocked state.

FIGURE 7.

Effect of extracellular magnesium on N63S hemichannel currents. (A) Representative hemichannel currents recorded from a N63S cRNA-injected oocyte in zero calcium MBS containing 0.5 mM [Mg²⁺]_o (upper panel) or 5.0 mM [Mg²⁺]_o (lower panel) . The cell was held at the hemichannel equilibrium potential (−10 mV) between pulse sequences to minimize holding currents. A 20-s conditioning voltage clamp pulse was applied to voltages between −80 and 20 mV followed by a test pulse to −80 mV. Data corrected for a linear leakage component. (B) Normalized G-V curves at different magnesium concentrations: 0.5 mM (open circles); 1.0 mM (solid triangles); 10 mM (solid squares). Normalized conductance (G/G_max) was determined at each potential by measuring the initial amplitude of the tail current during the test pulse to −80 mV and dividing it by the maximum value of the tail current obtained after a depolarization to +20 mV in the presence of 0.5 mM [Mg²⁺]_o. Symbols and bars indicate means ± SE. N = 4 or 5 experiments. (C) Steady-state channel availability curves for N63S: 1.0 mM [Mg²⁺]_o (open circles); 10 mM [Mg²⁺]_o (solid triangles). Symbols and bars indicate means ± SE. N = 4 or 5.

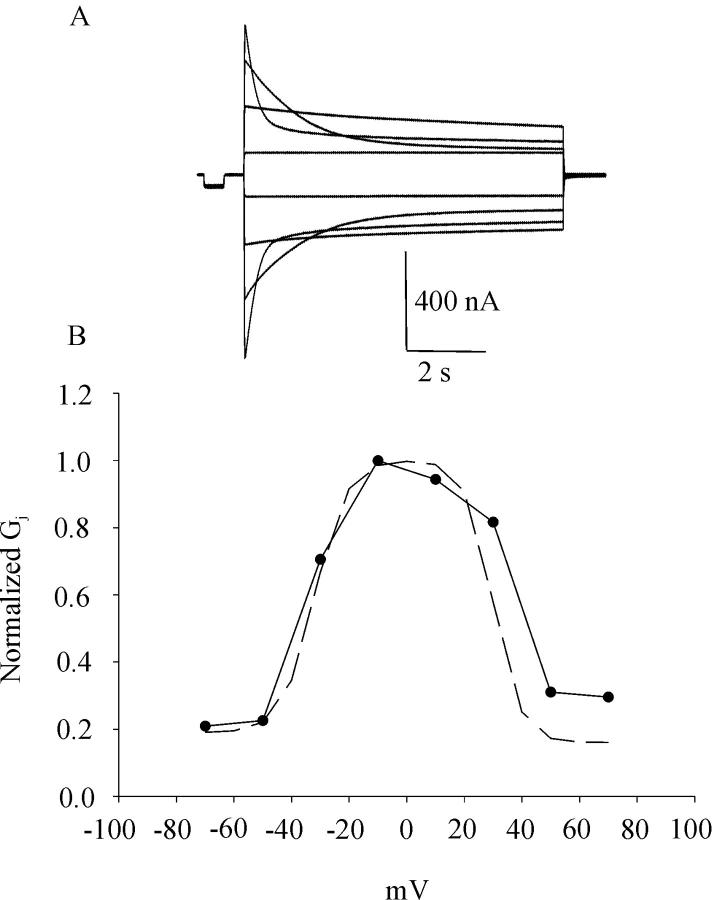
To elucidate the role of asparagine 63, we replaced asparagine 63 by the polar glutamine with a longer side. Unexpectedly, replacement of asparagine 63 by glutamine failed to produce functional hemichannels under standard conditions or in the presence of reduced extracellular divalent cations. However, the N63Q mutation was able to induce gap junctional conductances that were significantly higher than background when paired homotypically or heterotypically with hCx50 (Table 1). The mutation had no significant effect on V_j-dependent gating (Fig. 8). The G_j∞-V_j relationship for homotypic hCx46N63Q gap junctional channels was not significantly different from that of wild-type hCx46.

TABLE 1.

Gap junctional conductance of oocyte pairs expressing hCx46N63Q or wild-type hCx50

Oocyte Injection		Gap junctional coupling
Cell 1	Cell 2	Mean conductance, μS	n
hCx50wt	hCx50wt	20.5 ± 16.17a	21
hCx46N63Q	hCx46N63Q	1.136 ± 0.485	5
hCx46N63Q	hCx50wt	7.35 ± 10.32ab	26
hCx50wt	AS	0.115 ± 0.09	9
AS	AS	0.096 ± 0.1	12

Values are means ± SE; n, number of cell pairs.

^aP < 0.05 (Student's t-test compared to AS/AS).

^bP < 0.05 (Student's t-test compared to hCx50/AS).

FIGURE 8.

(A) Representative family of junctional current traces recorded from a cell pair injected with hCx46N63Q cRNA. Cells were initially voltage clamped at −40 mV. Junctional current traces were recorded in response to transjunctional voltage-clamp steps between +70 and −70 mV in 20-mV increments. (B) Normalized steady-state junctional conductance-voltage relationship for hCx46N63Q gap junctional channels (solid line). For comparison, the dashed line is the steady-state junctional conductance-voltage relationship for wild-type hCx46 gap junctional channels reported by Pal et al. (2000).

Discussion

In this study, we have characterized the effects of [Mg²⁺]_o and voltage on macroscopic hCx46 hemi-gap-junctional currents. Increasing extracellular magnesium resulted in a shift of the voltage dependence of activation to more positive potentials, a decrease in the maximum conductance, an acceleration of deactivation, and a slowing of activation. Hyperpolarizing the membrane potential could mimic the effect of raising of [Mg²⁺]_o on the activation kinetics and maximum conductance. We could reproduce the effects of magnesium on the G-V and steady-state availability curves using the kinetic scheme shown below:

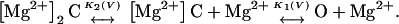In this model, magnesium enters the pore and blocks the channel in a voltage-dependent manner by binding to site 1. Binding of a second magnesium ion to site 2 stabilizes the channel in the closed/blocked state and makes it much more difficult for the channel to reopen. Two simplifying assumptions are made. The first assumption is that there is a clear temporal separation of the two kinetic activation phases: an extremely slow activation phase corresponding to the transition between [Mg²⁺]₂C and [Mg²⁺]C; and a fast activation phase corresponding to the transition between [Mg²⁺]C and O. This temporal separation allows the effect of magnesium on the first step in the deactivation process to be determined independently from the effect of magnesium on gating transitions between more remote closed states. The second assumption is that the transition between [Mg²⁺]₂C and [Mg²⁺]C depends on magnesium binding to a second site that is accessible from the outside only when the channel is closed. To estimate the parameters for magnesium binding, the data in Fig. 9, A and B were simultaneously fit to the following equations:

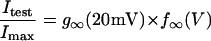(1)

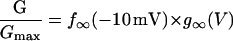(2)

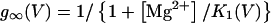(3)

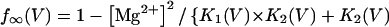(4)

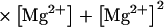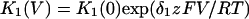(5)

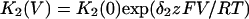(6)

Where K₁(0) and K₂(0) are the equilibrium dissociation constants for magnesium binding at sites 1 and 2 at zero voltage, respectively, z is the valence of the blocking ion, and δ₁ and δ₂ are the fractional depth of the magnesium binding sites. The best global least squares fit was obtained using the parameters listed in Table 2.

FIGURE 9.

Effects of extracellular magnesium on the G-V and steady-state hemichannel availability curves predicted by the 2-independent binding site model. The G-V curves for wild-type and mutant hCx46 were measured at the indicated extracellular magnesium concentrations. The steady-state hemichannel availability curves were measured at 1 and 10 mM [Mg²⁺]_o. The solid lines are the best global least squares fits of the data with the parameters given in Table 2. The data in A, B, C, and D are the same as that displayed in Figs. 1 D, 5 C, and 7, B and C, respectively.

TABLE 2.

Parameters for 2-independent binding site model determined from the overall least-squares fit

Hemichannel	X2+	K1(0) (mM)	δ1	K2(0) (mM)	δ2
wt hCx46	Mg2+	5.326	0.64	75.8	0.54
wt hCx46	Ca2+	0.38	1.0	0.04	0.54
hCx46*N63S	Mg2+	2.66	0.77	0.7	0.396

Analysis of the calcium data was complicated by the fact that effects of calcium on early transitions in the activation process were not well separated from its effects on later steps. However, to a first approximation, the equilibrium constants for the calcium blocking reaction could be determined by fitting the G-V curves in Fig. 2 C to Eq. 2. The best least square fit parameters are listed in Table 2. These data indicate that the K₁ and K₂ for calcium block were ∼10- and ∼1800-fold higher than those for magnesium, respectively.

Although we used a two-binding site model to account for the effects of divalent cations, some of the effects that we observe could also be accounted for by surface charge effects. For example, the positive shift in the G-V curve and the acceleration of channel closure with increasing divalent cation concentration could potentially be attributed to charge screening or screening plus binding leading to a reduction in surface potential. One argument against the charge screening hypothesis is that it requires that the hemichannels have an intrinsic voltage gating mechanism. However, voltage dependent gating completely disappears at hyperpolarized potentials in solutions containing no added divalent cations suggesting that divalent cations are an essential cofactor for hemichannel gating.

Role of the first extracellular domain in extracellular magnesium block

The first extracellular domain (E1) has been implicated in hemichannel gating. Expression studies in Xenopus oocytes have shown that the replacement of the first extracellular domain of rat Cx32 with that of Cx43 resulted in a chimeric gap junctional protein that could form functional hemichannels as well as gap junctional channels (Quist et al., 2000). In addition, Pfahnl and Dahl (1999) localized the voltage- and calcium-dependent gate of rat Cx46 hemichannels to this region using cysteine scanning mutagenesis. In the present study, we show that replacement of the highly conserved asparagine at residue 63 in E1 with serine strongly enhanced external magnesium block. The effect of the N63S mutation on the G-V and steady-state availability curves in the presence of various concentrations of [Mg²⁺]_o could be reproduced using the 2-independent binding site model using the parameters listed in Table 2 (Fig. 9, C and D). These results suggest that the predominant effect of the N63S mutation is a 17-fold increase in the apparent binding affinity of the second divalent cation binding site for magnesium. The large increase in binding affinity may indicate that asparagine 63 is directly involved in binding. Alternatively, mutating asparagine 63 may produce local or global structural changes that alter divalent cation binding.

To better understand the role of asparagine 63 in channel function, we replaced asparagine 63 with glutamine. The N63Q mutant failed to form functional hemichannels but could still form gap junctional channels that had normal gating properties. These results suggest that small perturbations at this position that do not cause a major structural rearrangement of the protein can have marked effects on hemichannel gating. Furthermore, these results support the idea that the hemichannel gate and the V_j gate are two separate entities.

Functional significance

In calcium-free medium, lens fiber cells have currents that closely resemble those elicited by Cx46 hemichannels in oocytes (Eckert et al., 1998). However, the high impedance of lens fiber cell membranes indicates that if these channels exist in the lens, they must normally be closed (Mathias et al., 1997). The strong dependence of hemichannel availability on resting membrane potential and external divalent cations is likely to serve as the primary mechanism for preventing the opening of hemichannels in the nonjunctional plasma membrane of the fiber cells. In this regard, it is interesting to note that previous studies have demonstrated a steep transjunctional voltage gradient from the cortex to the nucleus of the frog and mouse lens with the inner fiber cells being less negative (Mathias and Rae, 1985; Gong et al., 1998). According to our results, this reduction in transjunctional voltage might lead to an increase in hemichannel activity in the inner fiber cells. Hemichannels might also become activated under pathological conditions that result in depolarization of the fiber cells. Further studies are needed to clarify the role of gap-junctional-hemichannels in the lens under both physiological and pathological conditions.