19 Å Solution Structure of the Filarial Nematode Immunomodulatory Protein, ES-62

Abstract

ES-62, a protein secreted by filarial nematodes, parasites of vertebrates including humans, has an unusual posttranslational covalent addition of phosphorylcholine to an N-type glycan. Studies on ES-62 from the rodent parasite Acanthocheilonema viteae ascribe it a dominant role in ensuring parasite survival by modulating the host immune system. Understanding this immunomodulation at the molecular level awaits full elucidation but distinct components of ES-62 may participate: the protein contributes aminopeptidase-like activity whereas the phosphorylcholine is thought to act as a signal transducer. We have used biophysical and bioinformatics-based structure prediction methods to define a low-resolution model of ES-62. Sedimentation equilibrium showed that ES-62 is a tightly bound tetramer. The sedimentation coefficient is consistent with this oligomer and the overall molecular shape revealed by small angle x-ray scattering. A 19 Å model for ES-62 was restored from the small-angle x-ray scattering data using the program DAMMIN which uses simulated annealing to find a configuration of densely packed scattering elements consistent with the experimental scattering curve. Analysis of the primary sequence with the position-specific iterated basic local alignment search tool, PSI-BLAST, identified six closely homologous proteins, five of which are peptidases, consistent with observed aminopeptidase activity in ES-62. Differences between the secondary structure content of ES-62 predicted using the consensus output from the secondary structure prediction server JPRED and measured using circular dichroism are discussed in relation to multimeric glycosylated proteins. This study represents the first attempt to understand the multifunctional properties of this important parasite-derived molecule by studying its structure.

INTRODUCTION

Filarial nematodes are a group of arthropod-transmitted parasites of vertebrates. There are eight species which affect humans, three of which, Wuchereria bancrofti, Brugia malayi, and Onchocerca volvulus, are major causes of morbidity in the tropics (WHO, 1987). It is currently estimated that approximately 150 million people are infected with one or more of the latter three parasites with a further billion at risk. There are no entirely effective treatments available and presently no hope for a vaccine. Of those infected, a significant percentage will suffer serious health problems including chronic debilitating skin lesions, elephantiasis, and blindness.

Infection with filarial nematodes is lifelong and individual adult worms can survive for 5 years or more within the parasitized host (Vanamail et al., 1996). It is believed that they achieve this longevity through some form of modulation of the host immune system. Candidates for inducing this immunomodulation are products which are excreted or secreted (ES) by the filarial parasite. ES products are mainly glycoproteins, a number of which are covalently modified with phosphorylcholine (PC) groups (reviewed in Harnett and Harnett, 2001; Harnett and Parkhouse, 1995). The presence of PC on these proteins supports their possible immunomodulatory role as PC has previously been shown to have immunomodulatory capabilities (Mitchell and Lewers, 1976; Bordmann et al., 1998; Sloan et al., 1991).

The major ES product (ES-62) of the filarial parasite studied in our laboratories, Acanthocheilonema viteae, is a 57.8 kDa homolog of molecules found in human filarial nematodes. ES-62 is a glycoprotein with PC attached to some of its N-linked carbohydrate chains (Harnett et al., 1993). Our previous work has shown ES-62 to modulate activation of lymphocytes via the antigen receptors by desensitizing members of the PI-3-Kinase and Ras MAPKinase signaling pathways (reviewed in Harnett and Harnett, 1999). The importance of the PC groups in ES-62 has been demonstrated by the finding that signaling events modulated by ES-62 can be mimicked by PC alone or by PC conjugated to bovine serum albumin (reviewed in Harnett and Harnett, 1999). However, the protein and carbohydrate content of ES-62 must also be important for function, as not all of the effects induced by ES-62 can be mimicked in this way and inasmuch as PC alone is immunomodulatory, it is ∼2 orders of magnitude less effective than when complexed to ES-62.

Although to date there has been much information generated regarding the various components of ES-62 (protein, carbohydrate, and PC) and its effects on the cells of the immune system, there is no structural information on the parasite product. Thus the way in which ES-62 may interact with other proteins (in the B cell signal transduction pathway, for example; see Harnett and Harnett, 2001), and structural characteristics which could possibly be exploited for drug and vaccine design remain unknown. The work presented here represents the first steps in gaining vital structural information about this important parasite molecule. The findings presented in this article were obtained using a complementary combination of biophysical methods and bioinformatics-based structure prediction approaches; these have allowed the determination of the tetrameric nature of ES-62 and 19-Å models of the protein.

MATERIALS AND METHODS

Bioinformatics

A primary sequence similarity search of the nonredundant (nr) database was performed using the BLOSUM 62 matrix in the position-specific iterated basic local alignment search tool (PSI-BLAST; see Altschul et al., 1997; see http://www.ncbi.nlm.nih.gov/BLAST). The sequences with the highest significant homology to ES-62 obtained from this search were aligned using the program MULTALIN (Corpet, 1988; see http://prodes.toulouse.inra.fr/multalin/multalin.html) using progressive pairwise alignments. The multiple alignment was used as input for the web-based secondary structure prediction server, JPRED (Cuff et al., 1998; Cuff and Barton, 1999; see http://www.compbio.dundee.ac.uk/∼www-jpred/submit.html), which runs seven different secondary structure prediction programs, compares the results from each for every section of the protein and gives an output determined by the consensus from this comparison. In addition to the final JPRED report, the outputs from the other programs run by JPRED are also provided. Identification of proteins similar to monomeric ES-62 on the basis of secondary rather than primary structure was achieved using the program sss_align (Sturrock and Dryden, 1997) which compares the predicted secondary structure sequence (typically the output from the secondary structure prediction program PHD (Rost, 1996), one of the seven programs run by JPRED) of the protein of interest with those for a subset of the Protein Data Bank (PDB) (Berman et al., 2000; see http://www.rcsb.org/pdb/). A PAM (percent accepted mutation) value of 250 (midway between the strictest and most relaxed scoring schemes) and a QVAL of 75 (which gave the optimal statistical significance in the alignments) were used. No GAPOPEN or GAPEXTEND penalties were specified and the default database of 2000 proteins, supplied with the program, was used.

Preparation of ES-62

ES-62 was prepared as previously described (Harnett and Harnett, 1993). Jirds (Meriones libycus) were injected subcutaneously with A. viteae infective larvae and the animals sacrificed 8 weeks later for harvesting of the now mature adult worms. The recovered worms were kept in tissue culture flasks in RPMI (Rosweli Park Memorial lnstitute) complete medium at 37°C in an atmosphere of 5% CO₂/95% air where they secreted ES-62 into the medium. The spent culture medium was then filtered through a 0.22 μm membrane filter (to remove the larval microfilaria forms produced by adult females) and concentrated and exchanged with buffer A (5.5 mM KCl, 145 mM NaCl, 8mM Na₂HPO₄, 1.5 mM NaH₂PO₄, pH 7.4) via a pressure-driven stirred ultrafiltration cell (Millipore, Upper Mill Stonehouse, UK) with a PM10 membrane. The ES-62 was then further concentrated using centrifugal microconcentrator tubes (Millipore) with a 100 kDa cutoff membrane. The concentrated sample was then purified via FPLC (fast performance liquid chromatography) using a Superose 6 column. Ninety-five percent of the protein eluted as a single peak that could be identified (via Western blotting) as ES-62.

Circular dichroism

Far-UV circular dichroism (CD) spectra for ES-62 at 1.0 mg ml⁻¹ in 8 mM Na₂HPO₄, 1.5 mM NaH₂PO₄, 150 mM NaF, pH 7.0 were obtained on station 3.1 at the Synchrotron Radiation Source, Daresbury Laboratory and for ES-62 at 0.33 mg ml⁻¹ in 91.5 mM Na₂HPO₄, 58.5 mM NaH₂PO₄, pH 7.0 in a 0.02-cm pathlength quartz cell on a JASCO J-600 spectropolarimeter at the Scottish CD Facility, University of Glasgow.

Inductively coupled plasma atomic emission spectroscopy

To identify metal ions associated with the protein, an inductively coupled plasma atomic emission spectrum for ES-62 at 1 mg ml⁻¹ in buffer A (see above) was obtained on a Thermo Jarrell Ash (Franklin, MA) IRIS inductively coupled plasma atomic emission spectrometer at the Department of Chemistry, University of Edinburgh.

Sedimentation equilibrium

Sedimentation equilibrium (SE) experiments were carried out in a Beckman (Palo Alto, CA) Optima XL-A analytical ultracentrifuge (AUC). The experiments were performed at 4°C and at rotor speeds of 8 k and 10 k rpm. Scans were obtained at each speed until satisfactory overlay of traces separated by 3 h was obtained indicating attainment of equilibrium. Nine samples of ES-62 in buffer A (see above) at concentrations of between 0.9 and 5.2 μM were loaded into six-channel Yphantis-type centerpieces. Data were the average of 10 scans obtained in continuous mode with a 0.001 cm radial step size over the radial range 5.8–7.2 cm. The optical baseline was obtained by increasing the speed of the rotor to 40 k rpm.

The partial specific volume of ES-62 (0.73 ml g⁻¹) was calculated from the partial specific volumes of the constituent amino acids (Perkins, 1986) and carbohydrates and the buffer density at 4°C (1.00663 g ml⁻¹) was calculated using the program SEDNTERP (Laue et al., 1992). The SE data were analyzed following the procedure outlined by Byron et al. (1997) to obtain values for the apparent whole-cell weight-average mass (M_w,app) and the dissociation constant (K_d).

Sedimentation velocity

Sedimentation velocity (SV) experiments were carried out in a Beckman (Palo Alto, CA) Optima XL-A AUC. The experiments were performed at 4°C and at a rotor speed of 30 k rpm. A series of 32 scans, 15 min apart, was obtained for each sample. Samples of ES-62 in buffer A (see above) at four concentrations between 1.7 and 6.9 μM were loaded into double-sector centerpieces. Scans were obtained in continuous mode with a 0.002 cm radial step size and five averages. Finite element solutions of the equations governing sedimentation and diffusion (the Lamm equations) were obtained using the program SEDFIT (Schuck, 2000; see http://www.AnalyticalUltracentrifugation.com/). The sedimentation coefficient was obtained from the resultant fits to the sedimentation boundaries.

Small-angle x-ray scattering

Small-angle x-ray scattering (SAXS) experiments were carried out on the EMBL station X33 (Koch and Bordas, 1983; Boulin et al., 1988; Gabriel and Dauvergne, 1982) on the storage ring DORIS III of the Deutsches Elektronen Synchrotron with multiwire proportional chambers with delay line readout (Gabriel and Dauvergne, 1982). X-rays were scattered from ES-62 in PBS (phosphate buffered saline) pH 7.4 at concentrations of between 8.00 and 0.25 mg ml⁻¹. The reference solvent was PBS pH 7.4. The sample-detector distances were 3.4 and 1.9 m, covering the ranges of momentum transfer of 0.13 nm⁻¹ < s < 2.0 nm⁻¹ and 0.5 nm⁻¹ < s < 3.7 nm⁻¹, respectively (s = 4π sin θ/λ; 2θ is the scattering angle and λ = 0.15 nm is the x-ray wavelength).

The data were normalized to the intensity of the incident beam, corrected for the detector response, the scattering of the buffer was subtracted, and the difference curves were scaled for concentration. All procedures involved statistical error propagation using the program SAPOKO (Svergun and Koch, unpublished). Data at low angles were extrapolated to zero concentration following standard procedures (Feigin and Svergun, 1987). The data collected at the two camera lengths were merged to yield the final composite scattering curve.

The maximum dimension of the particle in solution D_max was estimated using the orthogonal expansion program ORTOGNOM (Svergun, 1993). The forward scattering intensity at zero angle I(0), distance distribution function p(r), and radius of gyration R_g were evaluated with the indirect transform package GNOM (Svergun et al., 1988; Svergun, 1992). For the computation of the Porod (1982) volume V_p a constant was subtracted from the experimental data to ensure that the intensity decays as s⁻⁴ following Porod's (1982) law for homogeneous particles. This procedure diminishes the scattering contribution due to the internal particle structure and yields an approximation of the “shape scattering” curve (i.e., scattering from the excluded volume of the particle filled by constant density).

Ab initio shape determination in small-angle scattering was first proposed by Stuhrmann (1970a) and further developed by Svergun et al. (1996) who employed nonlinear minimization to determine envelope functions parameterized using spherical harmonics. Recently, Monte Carlo based methods were proposed (Chacón et al., 1998; Svergun, 1999; Walther et al., 2000) yielding models in the form of finite volume element ensembles. In the present work, the method of Svergun (1999) was used. A sphere of diameter D_max is filled with densely packed small spheres (dummy atoms) of radius r₀ ≪ D_max. The structure of this dummy atom model (DAM) is defined by a configuration vector X assigning an index to each atom corresponding to solvent (0) or solute particle (1). The scattering intensity (I(s)) from the DAM is computed as

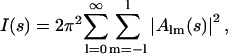(1)

where the partial amplitudes are (Svergun, 1999; Stuhrmann, 1970b):

(2)

Here, v_a = (4πr₀³/3)/0.74 is the displaced volume per dummy atom; the sum runs over the atoms with X_j = 1 (particle dummy atoms); r_j and ω_j are their polar coordinates; and j_l(x) denotes the spherical Bessel function. In keeping with the low resolution of the solution scattering data, the method searches for a configuration X minimizing the function f(X) = χ² + αP(X). Here, χ² is the discrepancy:

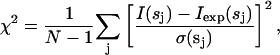(3)

where N is the number of experimental points, and I(s), I_exp(s), and σ(s) denote the calculated intensity, the experimental shape-scattering intensity and its SD, respectively. The penalty term P(X) taken with a positive weight α > 0 ensures that the DAM has low resolution with respect to the packing radius r₀. The minimization is performed starting from a random configuration using the simulated annealing method (Kirkpatrick et al., 1983). The program DAMMIN (Svergun, 2000; Svergun et al., 2000) makes it possible to also take into account information about the point symmetry of the molecule (for details of the method, see Svergun, 1999; 2000; Svergun et al., 2000).

RESULTS AND DISCUSSION

Characterization of ES-62 using bioinformatics-based structure prediction methods

ES-62 has primary structure homologs

PSI-BLAST (Altschul et al., 1997) identified six proteins (Table 1) homologous to ES-62. The level of identity between these proteins and ES-62 is between 37% and 39%, whereas the level of identity between these proteins (excluding ES-62) is between 87% and 97%. The multiple alignment of these proteins, performed using the program MULTALIN (Corpet, 1988), shown in Fig. 1 (combined with the secondary structure prediction for ES-62) suggests that these proteins belong to the same family and possibly have related functions and structures. The homologous proteins have diverse hypothetical or identified functions ranging from aminopeptidases to hematopoeitic switch proteins with unknown functions, none of which benefits from having a solved atomic resolution structure. This makes it difficult to predict the structure and function of ES-62 on the basis of primary sequence homology alone. Instead, the first structural predictions for ES-62 were made using secondary structure prediction programs.

TABLE 1.

Proteins with a high degree of primary sequence identity to ES-62

Protein	GenBank sequence number	% Identity with ES-62	% Identity with murine animopeptidase
Aminopeptidase (mouse)	5442032	38	—
Plasma glutamate carboxypeptidase;hematopoietic lineage switch 2 (mouse)	9055234	39	97
Liver annexin-like protein (rat)	7108713	39	92
Plasma glutamate carboxypeptidase (human)	5174627	38	87
Hematopoietic lineage switch 2 related protein (rat)	3851632	37	92
Aminopeptidase (human)	7706387	37	87

FIGURE 1.

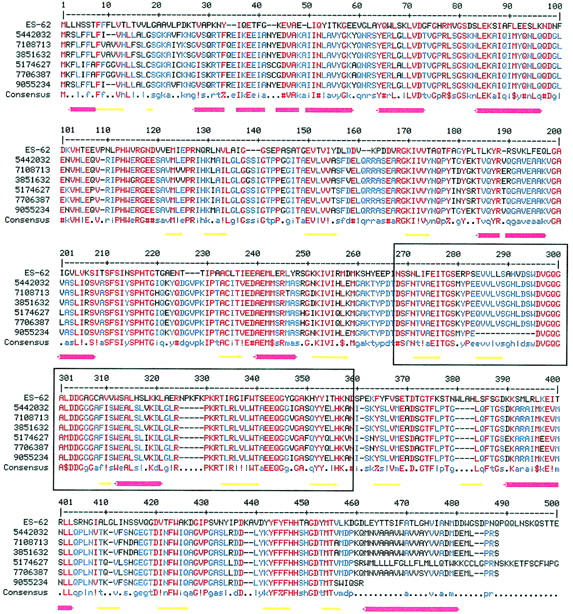
Multiple alignment of the amino acid sequence of ES-62 with those of its six protein homologs (Table 1). The multiple alignment was generated using MULTALIN (Corpet, 1988). The BLOSUM 62 matrix was used with a gap weight of 12 and a gap length weight of 2. The consensus levels were 90% for high homology (red) and 50% for low homology (blue). Symbols are as follows: ! is I or V; $ is L or M; % is F or Y; # is any one of NDQEBZ. The secondary structure for ES-62 predicted by JPRED (Cuff et al., 1998; Cuff and Barton, 1999) is shown beneath the alignment. Red cylinders represent α-helices and yellow arrows represent β-strands. In places helices appear broken reflecting the gaps inserted in the ES-62 sequence during alignment with its homologs. Boxed residues are those within ES-62 that are 32% identical with residues 74–168 of a leucyl aminopeptidase from Aeromonas proteolytica (PDB code, 1AMP).

The predicted secondary structure of ES-62

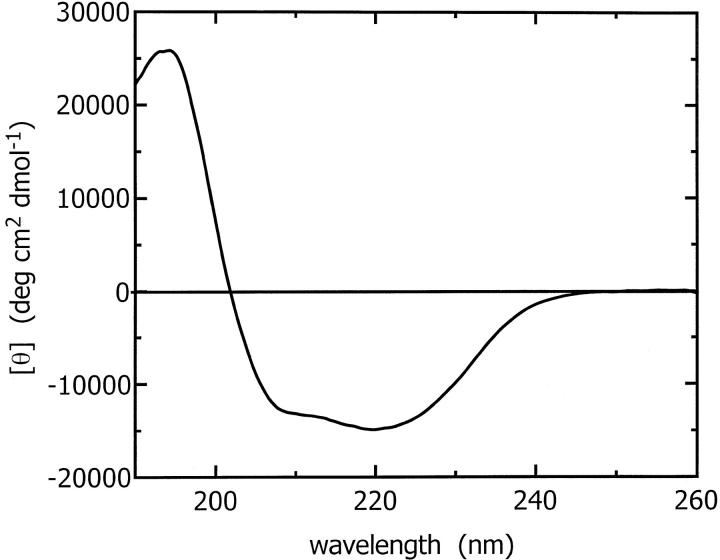
The secondary structure content of ES-62 predicted by JPRED (Cuff et al., 1998; Cuff and Barton, 1999) is 26% α-helix, 21% β-sheet, and 53% other. The predicted sequence of secondary structural elements is abstracted in Fig. 1. The secondary structure content of ES-62 was also determined experimentally by CD. Spectra from CD experiments performed at two laboratories using different concentrations of protein were compared; the results obtained were very similar with the normalized amplitudes within 5% of each other over the wavelength range studied. CD data from 240 to 190 nm (Fig. 2) were analyzed by the SELCON procedure (Sreerama and Woody, 1993) and indicated that ES-62 has 40% α-helix, 16% β-sheet, 16% β-turn, and 28% remainder. It should be noted that analysis of the CD data by the CONTIN procedure (Provencher and Glockner, 1981) gave a similar α-helix content (37%) but a somewhat higher β-sheet content (26%). In a number of studies on proteins with a significant proportion of α-helix, we have found that the CONTIN procedure tends to overestimate the β-sheet content (McDermott et al., 2001; White et al., 1993).

FIGURE 2.

Circular dichroism spectrum for tetrameric ES-62 at 0.33 mg ml⁻¹ in 91.5 mM Na₂HPO₄, 58.5 mM NaH₂PO₄, pH 7.0 buffer in a 0.02 cm pathlength quartz cell. The data were best fit with 40% α-helix, 16% β-sheet, and 16% β-turn.

The CD-derived estimates are significantly different from the predicted secondary structure pointing to limitations in secondary structure prediction or perhaps limited refolding of ES-62 upon tetramerization (the secondary structure prediction programs called by JPRED do not take into account quaternary structure information). Posttranslational modifications to the protein (glycosylation and phosphorylcholination) and its tetramerization may stabilize secondary structure elements otherwise not favored in the monomeric state. The accuracy of JPRED consensus secondary structure predictions for a set of 396 test proteins used by its authors to evaluate the program was 72.9% (Cuff and Barton, 1999). Thus we propose that the predicted secondary structure content is that of monomeric ES-62 lacking carbohydrate and PC.

ES-62 has secondary structure homologs

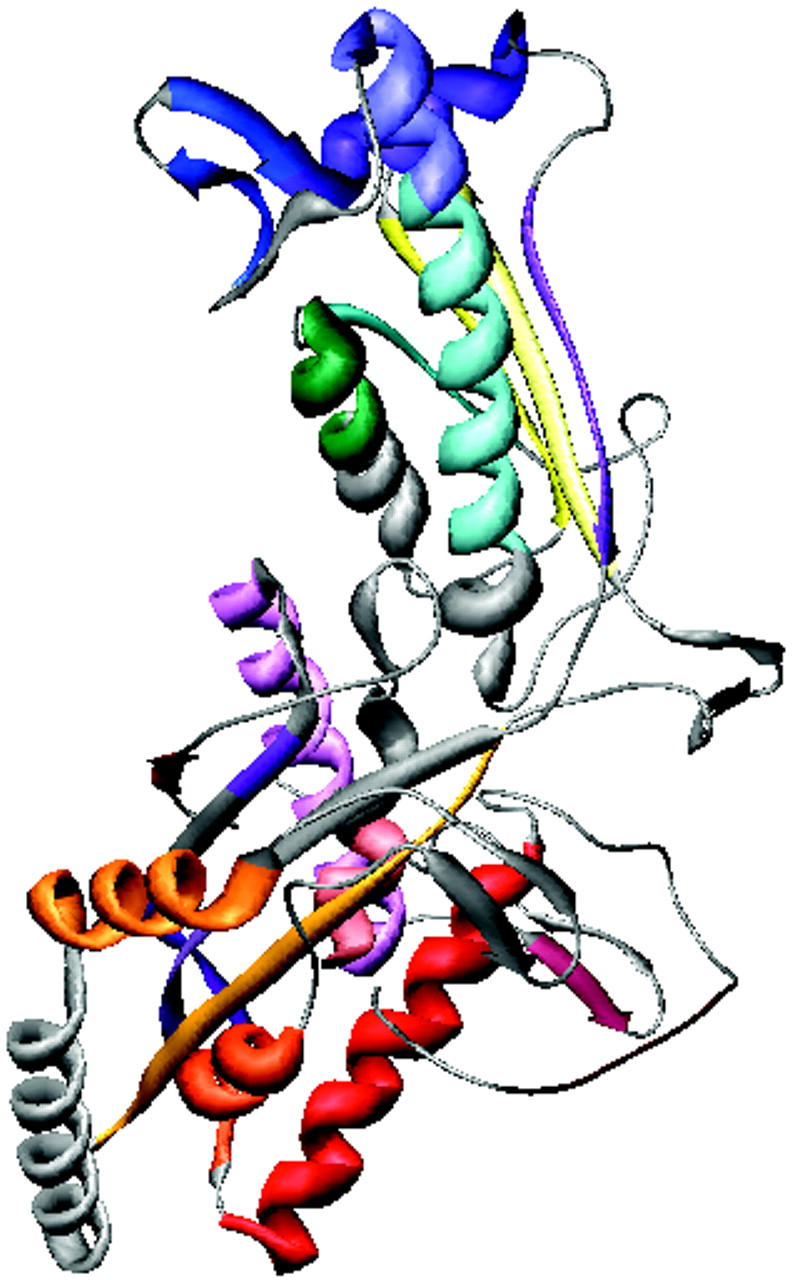
The predicted secondary structure sequence of ES-62 is similar to that of four proteins (Table 2) as determined by sss_align (Sturrock and Dryden, 1997). The identification of proteins similar to ES-62 in terms of secondary structure but not sequence is important as this information is valuable in the progression toward tertiary structure prediction. Homologous secondary structural elements have been colored the same in Table 2 (running from brown at the N terminus to pink at the C terminus). In all cases the homologous regions in the four proteins are smaller in size than ES-62 in its entirety. Subjective inspection reveals little overall fold similarity between these. An objective measure of shape similarity was obtained by comparison of solution SAXS curves calculated using the program CRYSOL ((Svergun et al., 1995) which uses multipole expansion of the scattering amplitudes of the constituent atoms to calculate the spherically averaged scattering pattern, taking into account the hydration shell) for the atomic coordinates of the regions of the four proteins found to be homologous with ES-62 (i.e., those presented in Table 2; also see Fig. 3). By this criterion the homologous regions of 1B0P and 1CX8 appear to have similar solution shapes; 1QJ2 is slightly different and 1FCE is very different.

TABLE 2.

Proteins with a high degree of secondary structure identity to ES-62

Protein	PDB Accession Code	Structure of homologous region
Pyruvate ferredoxin oxidoreductase from Desulfovibrio africanus (Rg = 26.4 Å; M = 41,958 Da)	1B0P
Ectodomain of human transferrin receptor (Rg = 24.9 Å; M = 45,920 Da)	1CX8
Endocellulase from Clostridium cellulolyticum (Rg = 22.5 Å; M = 50,799 Da)	1FCE
Carbon monoxide dehydrogenase from Pseudomonas carboxydovorans (Rg = 26.5 Å; M = 44,794 Da)	1QJ2

The radius of gyration (Rg) was calculated from atomic coordinates using the program CRYSOL (Svergun et al., 1995). The mass was calculated from the amino acid composition. Secondary structural elements are colored according to their position as follows:

Figure 14.

FIGURE 3.

Theoretical scattering curves for the four proteins, PDB codes 1B0P (solid line), 1CX8 (dashed line), 1FCE (dotted line), and 1QJ2 (dashed-and-dotted line), predicted to share a high degree of secondary structure homology with ES-62. The curves were calculated from the coordinates of the homologous region of the proteins using the software CRYSOL (Svergun et al., 1995). The homologous regions of 1B0P and 1CX8 have similar solution shapes; 1QJ2 is slightly different and 1FCE is very different.

Tertiary structure prediction

Several attempts were made to organize the predicted secondary structural elements of ES-62 into a folded tertiary structure. The programs PLOTCORR (Pazos et al., 1997) and DRAGON (Aszódi and Taylor, 1994; Aszódi et al., 1995; Taylor and Aszódi, 1994) were used to explore the predicted relationship between the constituent α-helices and β-strands in three dimensions and to fold these elements, de novo, into an α-carbon backbone. PLOTCORR predicts through-space contacts between amino acid residues within folded proteins using correlated mutations deduced from a multiple alignment of the sequence of the protein of interest and its primary sequence homologs in hssp (homology-derived secondary structure of proteins) format. DRAGON uses distance geometry to predict the tertiary structures of small soluble proteins on the basis of the amino acid sequence, predicted secondary structure, and additional optional information (such as solvent accessibility). Although neither program explicitly defines an upper mass limit, the larger the protein the more difficult it is to achieve a reliable prediction of residue contacts using PLOTCORR as the set of experimentally observed contacts becomes an increasingly smaller subset of all possible contacts (Göbel et al., 1994). Similarly, the hydrophobic core building heuristics of DRAGON cannot work with multiple domains or multiple hydrophobic cores typically found in larger proteins. For this reason we were unable to predict the tertiary structure of monomeric ES-62 in its entirety.

A small section of ES-62 (residues 254–345), 32% identical to residues 74–168 of a leucyl aminopeptidase from Aeromonas proteolytica (PDB code, 1AMP; see Schalk et al., 1992; Chevrier et al., 1994; Chevrier et al., 1996), was successfully modeled using the automated protein structure homology-modeling server Swiss-Model (Peitsch, 1996; Guex et al., 1999) with the short homologous section of 1AMP as a template (model not shown). This is, however, the only section of ES-62 for which there is a homologous high resolution structure. Unsurprisingly then, current bioinformatics-based structure prediction methods performed poorly for this complex glycoprotein.

Characterization of ES-62 using biophysical techniques

ES-62 requires the presence of a divalent metal ion

A strong magnesium signal was identified in the atomic emission spectrum obtained for ES-62 suggesting the requirement of this divalent cation in the protein. ES-62 has a putative metal coordination motif in its sequence (Harnett et al., 1999) and divalent cations are known to be critical to the function of aminopeptidases. The finding of metal ions was thus not unexpected and is consistent with one of the functions of ES-62.

ES-62 is tetrameric and slightly elongated

Sedimentation equilibrium data demonstrate that ES-62 is tetrameric and that the self-interaction occurs with high affinity. The apparent whole-cell weight-average molecular weight (M_w,app) was obtained by fitting the primary data with the equation describing the equilibrium distribution of a single thermodynamically ideal macromolecular solute (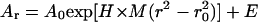) incorporated in the Beckman (Palo Alto, CA) XL-A analysis software. This model is a subset of a broader model (Eq. 4; Kim et al., 1977) which was then used to analyze the self-interaction implied by the observed elevation of M_w,app above the known monomer molecular mass. Eq. 4 describes a self-associating system defined by up to three association constants (K_a2, K_a3, and K_a4 in units of (absorbance)⁻⁽ⁿ⁻¹⁾) for oligomers composed of n₂, n₃, and n₄ monomers,

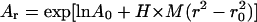(4)

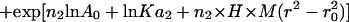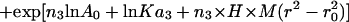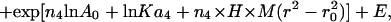where A_r is the absorbance at radial position r and A₀ is the absorbance at a reference position r₀ (cm); H is the constant 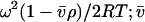is the partial specific volume of the macromolecule (ml g⁻¹); ρ is the solvent density (g ml⁻¹); ω is the rotor speed (radian s⁻¹); R is the gas constant (8.314 × 10⁷ erg K⁻¹ mol⁻¹); T is the temperature (K); M is the molecular weight of the solute (g mol⁻¹); and E is the optical baseline offset (obtained by overspeeding of the rotor).

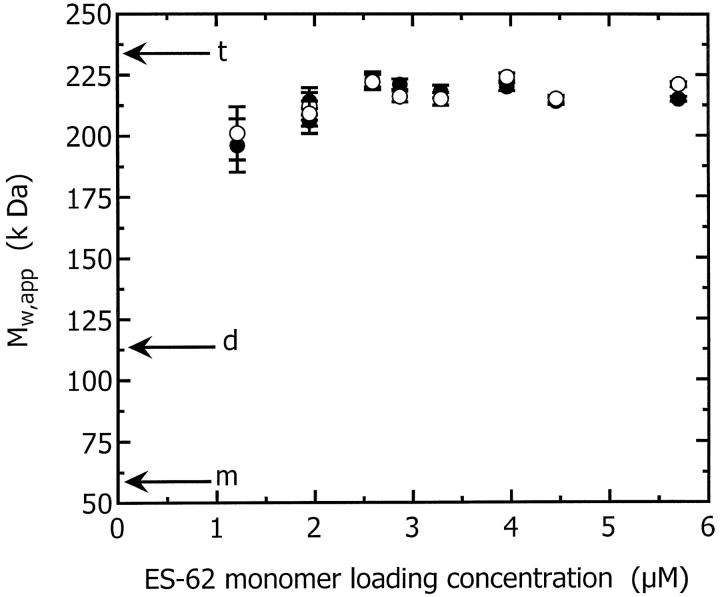
Good fits were obtained with the single species model for all the samples and the M_w,app values obtained are plotted in Fig. 4 as a function of concentration at both rotor speeds used: 8 k and 10 k rpm. From these data it is evident that the effective mass greatly exceeds the monomeric mass of ES-62 (57.8 kDa, calculated from the known amino acid, carbohydrate, and PC content) and is in fact close to the tetrameric mass (231.2 kDa). This increased mass indicates the presence of oligomers or high molecular weight aggregates. M_w,app does not change significantly with a change in rotor speed. In particular it does not decrease at the higher rotor speed indicating that the increase in mass, above that of the monomer, is due to self-association, not aggregation.

FIGURE 4.

M_w,app plotted as a function of ES-62 monomer loading concentration from sedimentation equilibria obtained at rotor speeds of 8 k rpm (•) and 10 k rpm (○). The molecular weights of ES-62 monomer, dimer, and tetramer are indicated by arrows annotated m, d, and t, respectively.

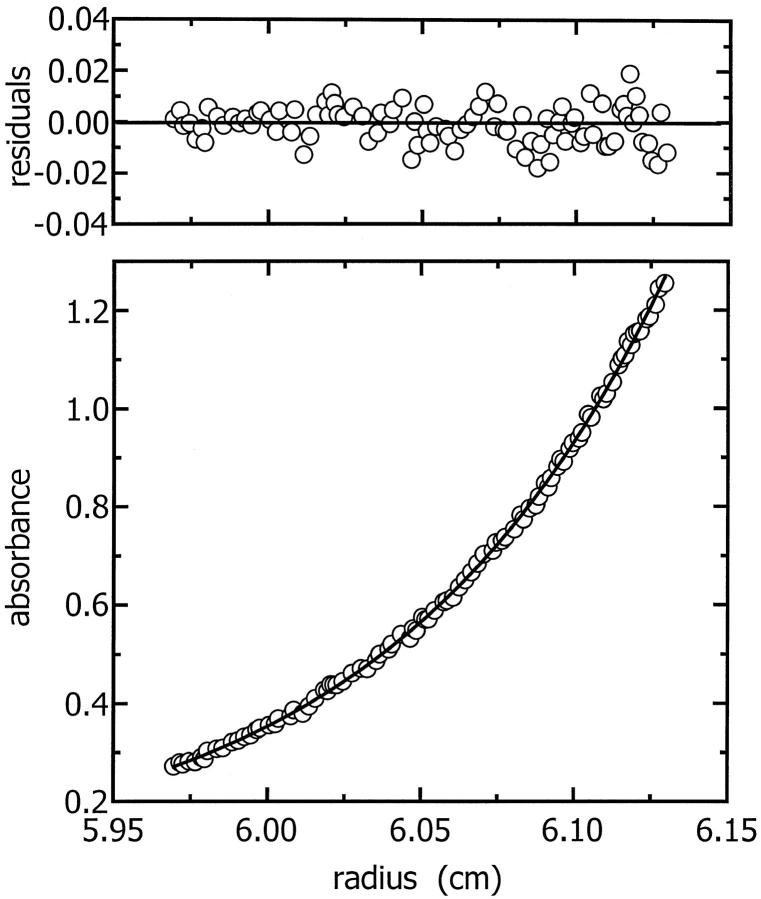
To ascertain the stoichiometry and strength of this self-interaction, the data were fitted with Eq. 4. Fits were attempted with a number of plausible models: monomer-dimer, monomer-tetramer, and dimer-tetramer. For the dimer-tetramer model, K_a2−4 was fitted by setting the monomeric mass at twice the actual monomer value (i.e., dimer mass) then fitting a monomer-dimer model to the data. Monomer-tetramer models could be fitted to some of the data but the fits and the residuals of the fits were poor. The dimer-tetramer model was the model which best described the data and a representative fit is shown in Fig. 5.

FIGURE 5.

A representative fit of the dimer-tetramer model to the sedimentation equilibrium primary data. The residuals of the fit are shown in the top panel.

The K_a values obtained from the fits to each of the SE data sets were converted first to units of M⁻⁽ⁿ⁻¹⁾ and then to dissociation constant (K_d) values. The conversion to M⁻⁽ⁿ⁻¹⁾ units was achieved using Eq. 5,

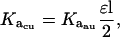(5)

where K_acu is the association constant in units of M⁻⁽ⁿ⁻¹⁾, K_aau is the association constant in units of absorbance⁻¹, ɛ is the extinction coefficient (for ES-62 this was determined via a Bradford assay to be 2.31 × 10⁵ cm⁻¹M⁻¹), and l is the path length of the AUC cell centerpiece (1.2 cm). The conversion to dissociation constants was achieved using Eq. 6,

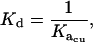(6)

where K_d is the dissociation constant (M⁽ⁿ⁻¹⁾).

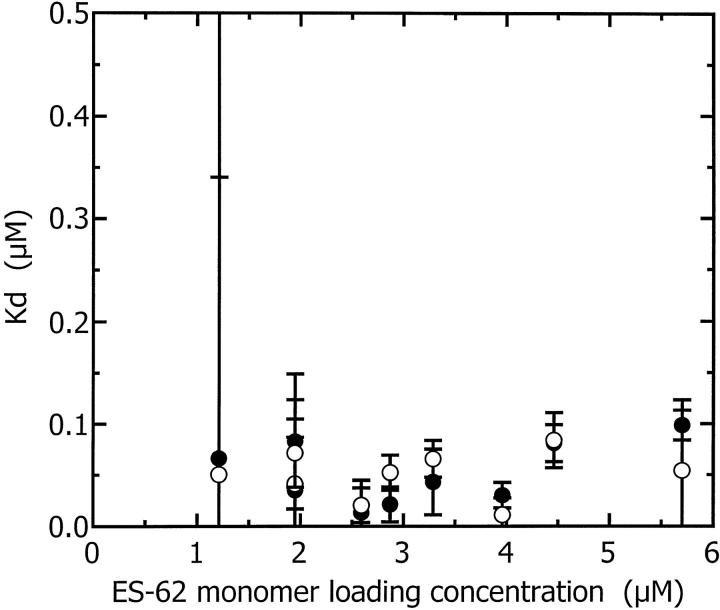
The K_d values determined at both 8 k and 10 k rpm are plotted as a function of concentration in Fig. 6. The dissociation constant of 50 nM indicates a strong association between the dimers to form tetramers. Thus, at the concentrations used in all biophysical studies in this article, the majority of ES-62 is tetrameric. This substantiates previous gel filtration studies which also demonstrated the tetrameric nature of the molecule (Harnett et al., 1993). That ES-62 is best modeled as a dimer-tetramer system is of further interest: ES-62 has previously been shown to possess aminopeptidase activity (Harnett et al., 1999) and the biologically active forms of many aminopeptidases are dimeric or tetrameric (Taylor, 1993; Acosta et al., 1998).

FIGURE 6.

Dissociation constant (K_d) (obtained from fitting the dimer-tetramer model to each of the sedimentation equilibrium primary data sets) plotted as a function of ES-62 monomer loading concentration and rotor speed, 8 k rpm (•); 10 k rpm (○).

Sedimentation coefficients generated from sedimentation velocity data (s_t,b) using the program SEDFIT (Schuck and Demeler, 1999) were converted to standardized values: those that would be measured at 20°C in water (s_20,w) using Eq. 7,

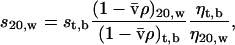(7)

where ρ is the density of water at 20°C or buffer at t°C, and η is the viscosity of water at 20°C or buffer at t°C. The program SEDNTERP (Laue et al., 1992) was used to calculate values of viscosity and density.

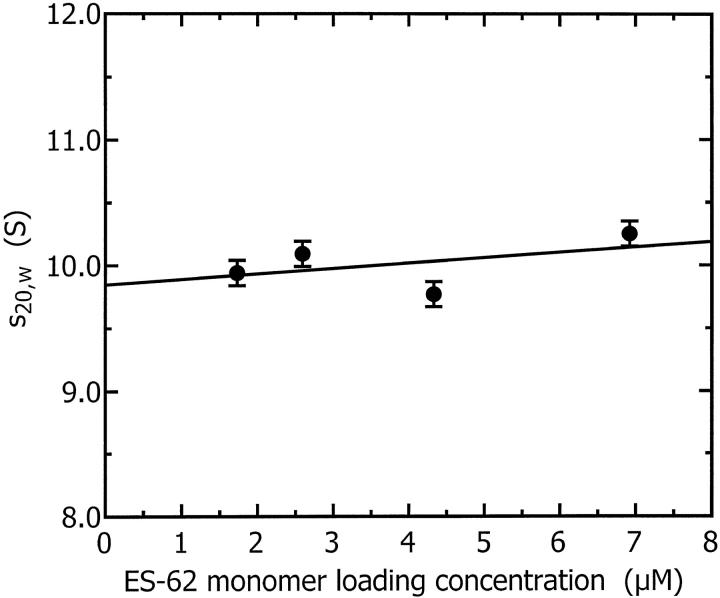
These sedimentation coefficients are plotted as a function of concentration in Fig. 7. The infinite dilution sedimentation coefficient obtained by extrapolation of these data to zero concentration is 9.85 ± 0.25 S. A sphere with the same mass as monomeric ES-62, hydrated with 0.4 g water/g protein (a typical protein hydration; see Squire and Himmel, 1979) would have a sedimentation coefficient of 4.6 S; a sphere with the same mass as tetrameric ES-62, similarly hydrated, would have a sedimentation coefficient of 11.7 S. The experimental sedimentation coefficient obtained is much larger than that predicted for the spherical monomer and smaller than that calculated for the hydrated tetramer. This confirms that ES-62 is likely to be a tetramer and suggests that it is normally hydrated and slightly elongated in shape or highly hydrated and almost spherical.

FIGURE 7.

Sedimentation coefficient as a function of ES-62 monomer loading concentration. The infinite dilution sedimentation coefficient obtained by extrapolation of these data to zero concentration is 9.85 ± 0.25 S.

ES-62—a low-resolution quaternary structure

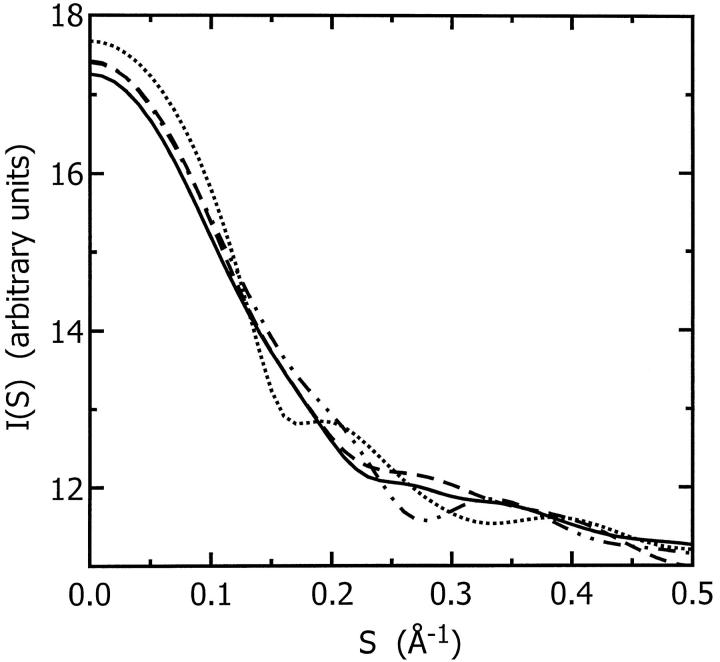
The maximum dimension and the radius of gyration of ES-62 computed from the composite scattering curve in Fig. 8 using the program GNOM (Semenyuk and Svergun, 1991; Svergun, 1992) are 13.0 ± 1 nm and 4.08 ± 0.03 nm, respectively. The Porod volume (i.e., excluded volume of the hydrated protein) is V_p = 400 ± 20 nm³. The volume of tetrameric ES-62 calculated from its mass and partial specific volume is 280 nm³. Thus the DAM contains 120 nm³ of bound water. The weight of each ES-62 tetramer is 3.84 × 10⁻¹⁹ g; the weight of the bound water is 1.20 × 10⁻¹⁹ g. This represents a hydration of 0.31 g water/g protein.

FIGURE 8.

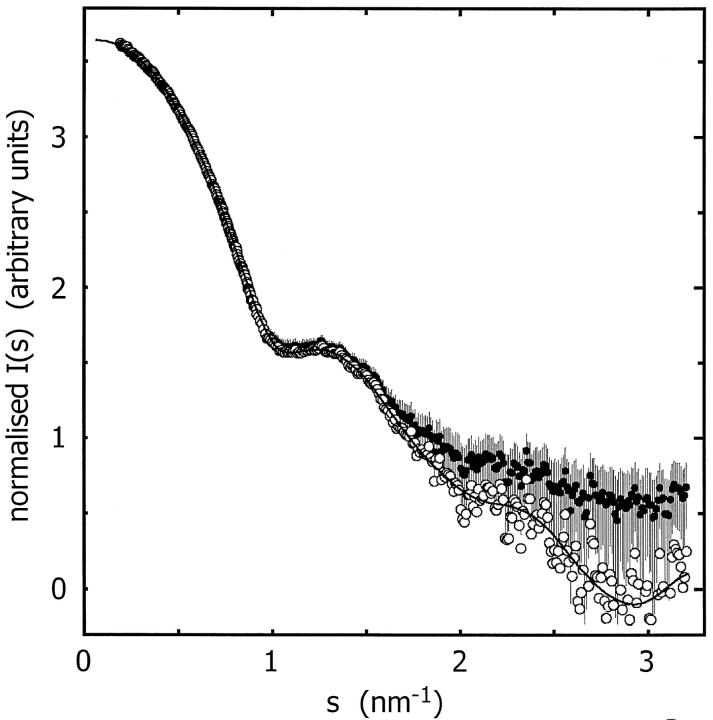
Composite experimental scattering pattern from ES-62 (•, with error bars), shape-scattering curve (○) and the scattering curve from the ab initio restored model (——).

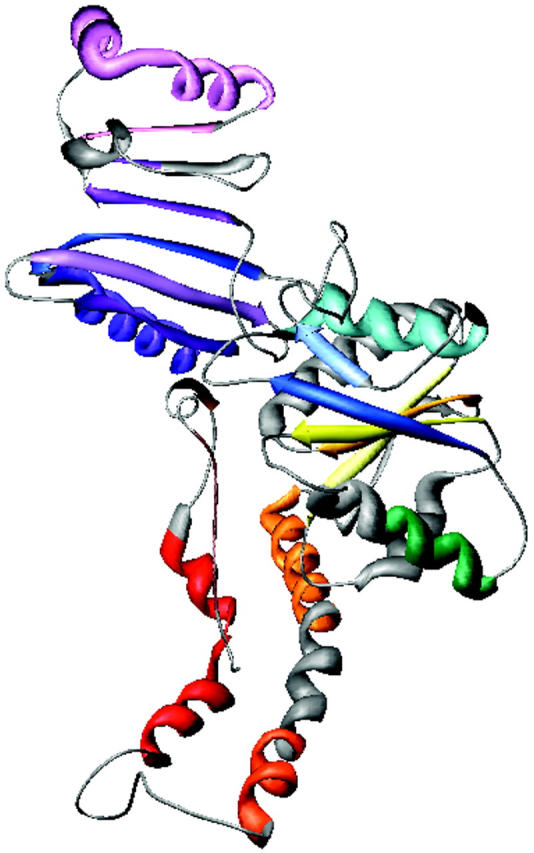
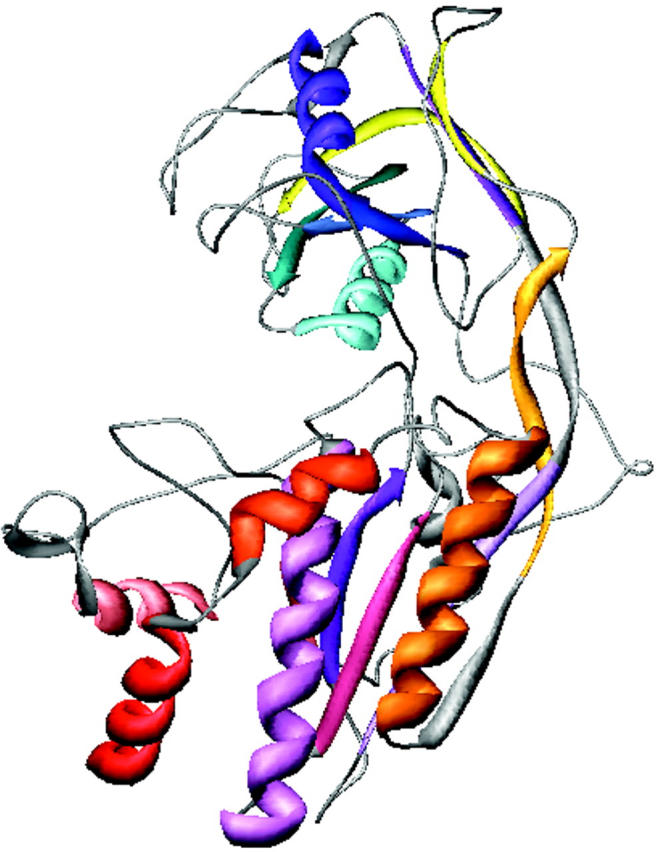
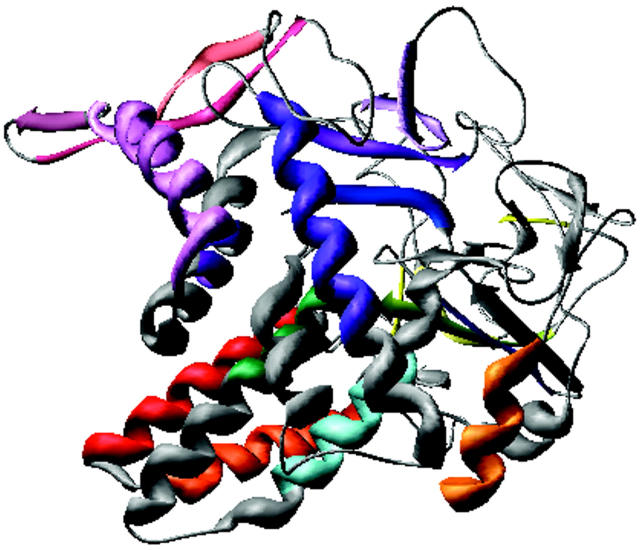
The low-resolution shape of the ES-62 was restored ab initio under three conditions from the experimental data as described in Materials and Methods; it was assumed that the particle possessed no symmetry, 2-point symmetry, or 222-point symmetry. Several independent restorations performed at the packing radii of the dummy atoms r₀ = 0.4–0.5 nm starting from different random approximations yielded reproducible results. All reconstructions, with and without symmetry restrictions, gave virtually the same fit to the experimental data with χ = 0.50 (Fig. 8). The calculated scattering curve (solid line) fits neatly the “shape scattering” pattern (open circles) and at higher angles goes below the initial experimental data (filled circles and error bars). This kind of fit is not unexpected, as the outer (high angle) portion of the experimental scattering pattern contains contributions from the internal structure poorly suited to this type of shape determination. Fig. 9 shows typical restored shapes obtained from imposing no symmetry, 2-point, or 222-point symmetry. The most information can be seen in the restored shape where 222-point symmetry was imposed (right column of Fig. 9). In this figure ES-62 appears as an assembly of two dimers tilted by ∼30° with respect to the long axis of the particle.

FIGURE 9.

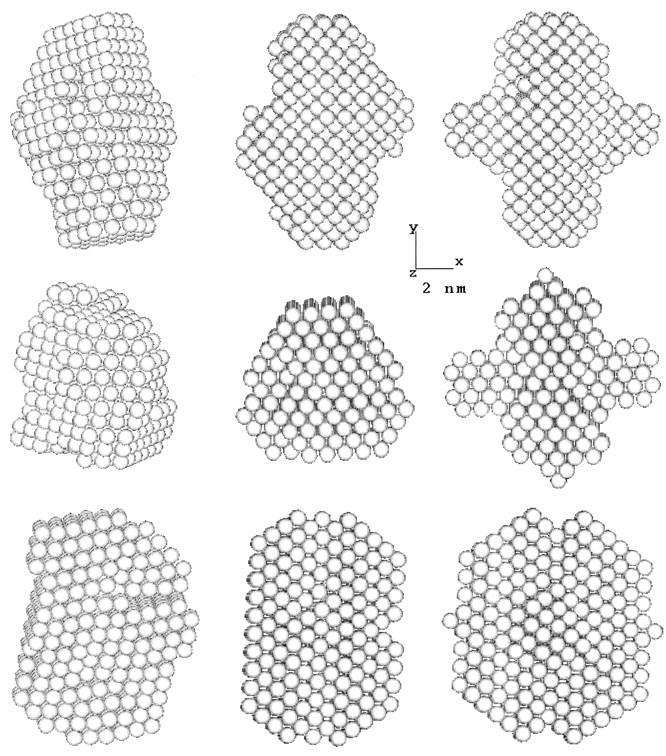
Orthogonal views (top to bottom) of the low-resolution dummy atom model of ES-62 restored assuming point symmetries of (left to right) 1, 2, or 222.

ES-62 is a glycoprotein with three glycosylation sites. The presence of extended, flexible heterogeneous carbohydrate, coupled with restrictions on the amounts of wild-type protein available and its stability, make the determination of a high-resolution structure by x-ray crystallography a difficult task. SAXS was employed as a method of obtaining structural data which could be used to model the three-dimensional structure of the protein in a near-physiological environment. Apart from DAMMIN (Svergun, 1999), there are at least three programs that restore low-resolution structures from SAXS data: Dalai_GA (Chacón et al., 1998, 2000; http://akilonia.cib.csic.es/DALAI_GA2/; the program employs a genetic algorithm for bead modeling within a search volume), Saxs-3D (Walther et al., 2000) using a pure Monte Carlo search on an unbound regular grid of knots, and GASBOR (Svergun et al., 2001; see http://www.embl-hamburg.de/ExternalInfo/Research/Sax/program.html; this method represents a protein as an ensemble of dummy residues and is able to also fit wide angle data). In this instance DAMMIN was used because it was written by one of the coauthors of this paper (D.I.S.) and it permits modeling using symmetry restrictions on the solution. The resolution of the model (19 Å) is an order-of-magnitude lower than a crystallographic structure, but nonetheless greater in resolution than a simple radius of gyration or axial ratio (based only on a sedimentation coefficient). However, the sedimentation coefficient is used as a valuable additional constraint on the SAXS model.

The program HYDROPRO (García de la Torre et al., 2000) was used to calculate a sedimentation coefficient for the DAM of ES-62. HYDROPRO calculates hydrodynamic parameters for shell models which it constructs from user input files of model coordinates. To ensure that the primary hydrodynamic model was properly filled with overlapping spheres we selected a radius for the atomic elements in excess of the radius of the dummy atoms which, in the DAM, are arranged as hexagonally packed, nonoverlapping spheres. The packing radius of the DAM was 4.5 Å; therefore, an atomic element radius of 6.0 Å was used for the HYDROPRO model. The maximum minibead radius was 5.0 Å and the minimum 3.0 Å. The sedimentation coefficient calculated by HYDROPRO for the shell-model limit with these parameters was 10.19 S. The effective hydrodynamic volume of this model was 471.9 nm³ whereas the volume of the anhydrous glycoprotein (calculated from its mass and partial specific volume) is 280.3 nm³. Thus the effective hydration is 0.5 g water/g protein (García de la Torre, 2001). This is in acceptable agreement with the hydration of the DAM (0.31 g water/g protein) and with the experimental sedimentation coefficient (9.85 ± 0.25 S). In summary, the 19 Å model restored from SAXS data is consistent with the hydrodynamic data from the AUC.

According to the sampling theorem (Shannon and Weaver, 1949; Moore, 1980; Taupin and Luzzati, 1982) the number of degrees of freedom associated with the solution scattering curve in Fig. 8 is N_s = D_max s_max/π ≈ 13 where D_max is the maximum dimension of the macromolecule and s_max the reciprocal Bragg dimension. The models in Fig. 9 are formally described by a significantly larger number of parameters (they contain 650 dummy atoms in the independent part of the search volume). A natural question arises as to whether the information content in the scattering data justifies the unique ab initio restoration of such a model. It should be stressed that despite a small (0.4 nm) radius for the dummy atoms, the DAM is kept at low resolution by the looseness penalty during the shape determination process. The resolution of the models in Fig. 9 is defined solely by the range of the data fitted (2π/s_max ≈ 2 nm), and the number of independent parameters describing it. Thus its resolution (19 Å) is much lower than that of the dummy atoms (radius 4.5 Å). As demonstrated by Svergun (1999; 2000) by shape determination from experimental SAXS data of several proteins with known crystal structures, the ab initio method yields a good reconstruction of the quaternary structure. In this present study, the use of the symmetry restriction permits further enhancement of the capability of the shape reconstruction procedure. Computations without symmetry or with 2-point symmetry yielded overall shapes for the entire protein similar to that obtained from imposing 222-point symmetry. However, imposing the 222-point symmetry provides a much clearer visualization of the arrangement of the dimers in the tetramer.

First steps in a structural understanding of ES-62 function

Filarial nematodes constitute a group of medically important parasitic organisms whose control remains inadequate. It is generally accepted that there is much to be gained—vaccines and immunotherapy, for example, if we can understand their interaction with the immune system at the molecular level. ES-62 is undoubtedly a key player in this interaction. The broad range of immunomodulatory properties that we have shown it to possess in vitro virtually encapsulates the immunological phenotype observed during filarial nematode infection in its entirety (reviewed in Harnett and Harnett, 2001). Furthermore, we have shown the molecule (released in isolation from osmotic pumps implanted in mice to generate serum concentrations equivalent to those found during natural infection) to be highly active in vivo (Goodridge et al., 2001; E. H. Wilson, M. R. Deehan, E. Katz, K. S. Brown, K. M. Houston, M. M. Harnett, and W. Harnett, unpublished). Clearly there is a need to understand how this large, complex molecule has such a potent and all-consuming effect on the immune system. The results we have described in this study represent the first steps in addressing this critical question from a structural viewpoint. Confirmation of the tetrameric structure, for example, is consistent with the observed aminopeptidase activity (Harnett et al., 1999) and also raises the possibility as to whether oligomer-induced cross-linking of cell surface receptors (by PC?) could explain effects on lymphocyte signal transduction pathways. It is hoped we can pursue these important issues further by, for example, investigating the structural and functional properties of both monomerized and PC-free ES-62.