Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Jan;84(1):509–522. doi: 10.1016/S0006-3495(03)74870-X

Study of Binding between Protein A and Immunoglobulin G Using a Surface Tension Probe

L Yang 1, M E Biswas 1, P Chen 1
PMCID: PMC1302631  PMID: 12524303

Abstract

Molecular interactions and binding are one of the most important and fundamental properties in the study of biochemical and biomedical systems. The understanding of such interactions and binding among biomolecules forms the basis for the design and processing of many biotechnological applications, such as bioseparation and immunoadsorption. In this study, we present a novel method to probe molecular interactions and binding based on surface tension measurement. This method complements conventional techniques, which are largely based on optical, spectroscopic, fluorescence polarization, chromatographic or atomic force microscopy measurements, by being definite in determining molecular binding ratio and flexible in sample preparation. Both dynamic and equilibrium (or quasi-equilibrium) information on molecular binding can be obtained through dynamic and equilibrium surface tension measurements. For an important pair of biological ligand and ligate, Protein A and immunoglobulin G (IgG), the existence of molecular interactions and the binding ratio of 1:2 have been determined unequivocally with the proposed surface tension method. These results are confirmed/supported by a mass balance calculation and spectrophotometry experiment. In addition, adsorption isotherms for Protein A and IgG separately at the air/water interface have been established with the dynamic surface tension measurements. The results show that the Langmuir isotherm equation can describe the adsorption data satisfactorily for both Protein A and IgG solutions.

INTRODUCTION

Interactions and binding between biomolecules are one of the most important events in a wide variety of biochemical and biomedical processes. Examples are binding of ligands to proteins, enzyme-catalyzed chemical reactions, immune responses and signal transduction (Náray-Szabó, 1997; Rarbach et al., 2001; Lee et al., 2001; Caffrey, 2001; Pramanik et al., 2000). Studies of the interactions between a ligand and a target protein provide the information on the nature of the forces that determine the specific biological functions. This may give us better insight into many vital life and important bioengineering processes. The understanding of molecular interactions and binding also provides the basis for many biotechnology designs and processes, such as rational design of artificial affinity ligands for biopolymers purification (Náray-Szabó, 1997; Tashiro and Montelione, 1995).

The methods employed in the determination of ligand–protein interactions are often those of physical chemistry, which include optical (Rarbach et al., 2001; Pramanik et al., 2000; Anderson and Weber, 1969; McClure and Craven, 1974), spectroscopic (Jayaraman, et al., 2000), fluorescence polarization (Wu et al., 2000), chromatographic (Bjorklund and Hearn, 1997), radioactive (Spector et al., 1969), and atomic force microscopy (Takano et al., 1999; Merkel et al., 1999). Most of these approaches have limitations, and often require rather restrictive sample preparations (Rarbach et al., 2001; Anderson and Weber, 1969; McClure and Craven, 1974; Jayaraman, et al., 2000; Wu et al., 2000; Bjorklund and Hearn, 1997; Spector et al., 1969); therefore, it is somewhat difficult to measure the dynamic process of molecular interactions. Recently, surface tension (γ) measurement has been developed for studying protein–small molecule interactions (Chen et al., 1996, 1999). Through the analysis of the γ-response pattern, surface competitive adsorption between small organic molecules and protein molecules can be detected. Furthermore, the molecular binding can be studied in terms of dose effects and specificity. This method is flexible in its sample preparation and, more importantly, it is capable of conducting dynamic measurements and hence revealing dynamic aspects of molecular interactions.

However, there are some limitations for the current method to study molecular interactions by measuring the surface tension (γ) response to surface area changes (Chen et al., 1996, 1999). Although the method can detect the existence of molecular interactions, it cannot determine some detailed, important characteristics of such interactions, such as the number of binding sites on biomolecules or the binding ratio between the two molecules. The molecular binding ratio has been one of the most important aspects of molecular interactions. Frequently, binding ratios are considered to be an equilibrium parameter; this would require experimental data obtained from sample systems at equilibrium state. Thus, measurement of equilibrium surface tension would be necessary, as opposed to measurement of dynamic surface tension that was employed previously (Chen et al., 1996, 1999).

The principle of the surface tension measurement for detecting molecular interactions is as follows: molecular interactions usually induce changes in physicochemical properties of the molecules involved, e.g., proteins and lipids. Most biomolecules have some degree of surface activity, and can easily adsorb at the surface and hence modify the surface properties. One of the most significant surface properties is surface tension; measurement of surface tension changes will then reflect the interactions between the molecules. Because the surface adsorption and hence measurable surface tension changes need only small amounts of surface active materials adsorbed at the surface, the sample of limited quantity can be most efficiently used, as compared with those for bulk property measurement. As will be seen later, for example, the surface tension measurement is sensitive to protein concentrations as small as a few nanomolarities. In addition, the total solution volume required for the surface tension measurement can be of the order of 1 μl, because of the small size of a pendant drop used in the measurement. This is useful and necessary, in particular, for many biological samples, inasmuch as they are often very expensive to obtain, and also at low concentrations.

In this work, we study molecular interactions and binding between a pair of classical biological ligand and ligate: Protein A and immunoglobulin G (IgG), by measuring both equilibrium and dynamic surface tensions of the solutions of their mixtures. In particular, we show that the molecular binding ratio can be determined from measurement of equilibrium surface tension as a function of their relative concentration.

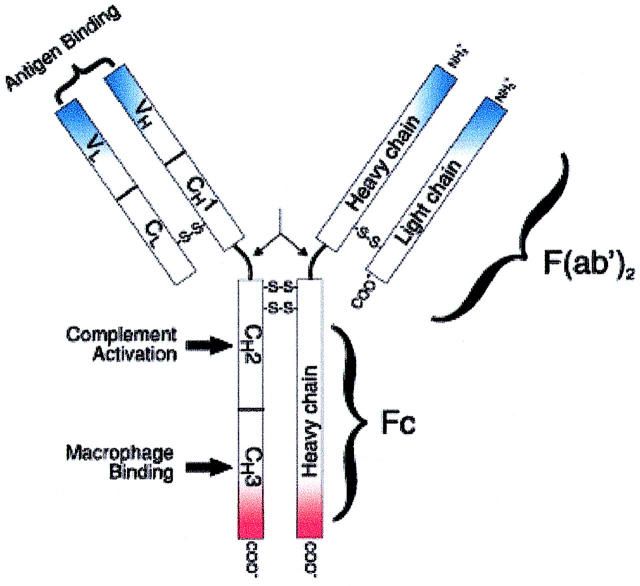
Immobilized Protein A adsorbents have been extensively used for purification of IgGs (Boyle et al., 1993; Hou et al., 1991; Klein et al., 1994) and removal of human IgG from plasma or serum in the treatment of immune-related diseases (Jones, 1990; Ikonomov et al., 1991; Jia et al., 1999). Protein A is a highly stable surface receptor with a molecular weight of 42 kDa. It can be produced by Staphylococcus aureus or by recombinant DNA technology. IgG (MW, 150 kDa) has a basic four-chain monomeric structure, consisting of two identical heavy chains and two identical light chains with interchain disulfide bonds. Each light chain has a molecular weight of 25 kDa and is composed of two domains, one variable domain (VL) and one constant domain (CL). Each heavy chain has a molecular weight of 50 kDa, and consists of one variable domain (VH) and three constant domains (CH1, CH2, and CH3). Between the CH1 and CH2 domains is the so-called hinge region, which permits flexibility between the two Fab arms of the Y-shaped antibody molecule (Fig. 1). This flexibility allows the two Fab arms to open and close, accommodating binding to two antigenic determinants separated by a fixed distance. Functionally, an IgG molecule can be divided into two portions: one is Fragment antigen binding (Fab) fragment, which is the antigen-binding site; the other is Fragment crystallizable (Fc) fragment, which has many effector functions, such as binding complement, and binding to cell receptors on macrophages and monocytes.

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic representation of an IgG molecule. IgG (MW, 150-kDa) have a basic four-chain monomeric structure consisting of two identical heavy chains and two identical light chains. The heavy chain contains one variable domain (VH) and three constant domains (CH1, CH2, and CH3). The region between the CH1 and CH2 is the hinge region and permits flexibility between the two Fab arms of the Y-shaped antibody molecule, allowing them to open and close to accommodate binding to two antigenic determinants separated by a fixed distance. Functionally, an IgG molecule can be divided into two portions: Fragment antigen binding (Fab) fragment, which is the antigen-binding site, and Fragment crystallizable (Fc) fragment, for which Protein A has high affinity.

The physicochemical properties of the Protein A-IgG binding have been investigated using x-ray crystallography (Deisenhofer, 1981), radioimmunoassay (Nardella et al., 1985; Vidal and Conde, 1985), and spectrophotometry (Sjöquist et al., 1972). It is known that Protein A has high affinity for the Fc portion of IgG (Boyle and Reis, 1987). The binding between Protein A and IgG leads to formation of Protein A-IgG complexes, which can precipitate out of the aqueous solution (Sjöquist et al., 1972). However, one of the most important characteristics of the binding, namely the binding ratio between Protein A and IgG, has not been determined undisputedly. From the UV absorbance, the amount of IgG in the precipitate of the Protein A-human IgG complex was calculated, and a molar ratio of 2.1:1, between IgG and Protein A, was obtained (Sjöquist et al., 1972). But from a sequence study of Protein A (Uhlén et al., 1984), five IgG binding domains on a Protein A molecule have been proposed. Further studies (Lindmark et al., 1981; Sjöholm, 1975) stipulated a 1:1 molar binding ratio. It is thus necessary and interesting to use an independent experiment to determine the binding ratio. This determination will have significant implications in many biochemical and biomedical applications; it will form the basis for evaluating the efficacy of immobilized Protein A adsorbents in IgG purification.

The proposed surface tension probe of molecular binding can be realized by many surface tension measurement techniques; typical ones are DuNuöy ring tensiometer (Suttiprasit et al., 1992.), the drop volume technique (Tornberg, 1978), the Wilhelmy plate technique (Paulsson and Dejmek, 1992), and the pendent drop technique (Ward and Regan, 1980). A detailed discussion about the four methods has been documented (Chen et al., 1996). In this study, we choose one of the pendent drop methods, Axisymmetric Drop Shape Analysis Profile, which is a novel technique to determine interfacial tensions from the shape of axisymmetric menisci (Rotenberg et al., 1983). Its basic principle is to fit the experimental drop profile to a theoretical one given by the Laplace equation of capillary, and the surface tension is generated as a fitting parameter. Details of the methodology and experimental setup can be found elsewhere (del Rio and Neumann, 1997, Neumann and Spelt, 1996).

It should be noted that the sample preparation for the Axisymmetric Drop Shape Analysis Profile measurement is straightforward, and much simpler than many other methods for studying protein interactions, such as those based on fluorescence, where a fluorescent dye is generally required in the compound of interest. Sometimes, the effect of the inclusion or creation of the fluorescent dye on the test compound has to be established before a meaningful binding experiment can be conducted. In addition, the pH of the solution can be adjusted readily in the surface tension measurement, whereas the fluorogenic substrate methods generally require basification of the medium to achieve optimal detection sensitivity (Gee et al., 1999). The rather restrictive sample preparation may also be seen in the atomic force microscopy-based methods, where immobilization of protein pairs to the atomic force microscopy tip and the scanning surface, respectively, must be accomplished before the binding energy can be explored (Takano et al., 1999, Merkel et al., 1999).

To complement the surface tension measurements, a mass balance analysis and spectrophotometry experiment are also performed. The mass balance analysis of the precipitate formed by Protein A–IgG complexes would give an estimate of the complex concentration with respect to initial monomer concentrations of Protein A and IgG, and hence confirm a molar binding ratio determined by the surface tension measurement. The spectrophotometry experiment is conducted as a function of time when Protein A is mixing with IgG in an aqueous solution. The measured UV absorbance would reflect the time sequence of complex formation and precipitation, and corroborate the dynamic surface tension measurement and hence reassure the equilibrium tension determination.

MATERIALS AND METHODS

Materials

Protein A, produced by Staphylococcus aureus, was from ProZyme (http://www.prozyme.com/technical/protadata.html). Human IgG (reagent grade) was obtained from Sigma Chemical Co. (St. Louis, MO). All other chemicals in analytical grade were from BDH. A 0.02 M Na2HPO4-NaH2PO4 buffer containing 0.15 M sodium NaCl (pH 7.4) was employed to prepare all protein solutions. The water used was purified by an Ultra-Pure Water System from Millipore Co., with resistivity of 18.2 M × Ω × cm.

Surface tension measurement with Axisymmetric Drop Shape Analysis Profile

With the use of a microsyringe, a pendent drop of the protein solution was formed at the tip of a vertical Teflon capillary of circular cross section (inner diameter, 1.5 mm), producing an axisymmetric boundary for the drop. The drop volume ranged from 0.02 to 0.002 ml, although typical values were ∼0.02 ml. The system was enclosed in a sealed environmental chamber saturated with water. The drop was illuminated with a white light source, model ACE from Schott-Fostec, shining through a heavily frosted glass diffuser. Images of the drop were obtained through a microscope, model 301310 from OPTEM International, which was linked to a monochrome charge-coupled device video camera, model COHU 4915 from Infrascan. The video signal was transmitted to a digital video processor DT3155 frame grabber board (Data Translation), which would perform the frame grabbing and digitization of the image to 640 × 480 pixels with 256 gray levels. For each protein concentration, the images were continuously captured until an approximately constant surface tension was obtained (see below). The entire setup was placed on a vibration-free table (Technical Manufacturing) to protect the system from external disturbances. All experiments were done at room temperature. The digitized images were analyzed and the surface tensions were obtained by fitting the experimental drop profile to a theoretical one governed by the Laplace equation of capillarity using the ADSA-P programs.

Dynamic surface tensions of individual proteins

To analyze the surface tension data of the protein mixtures, surface tensions of individual protein solutions would be needed. The difference in surface tension between the mixed solutions and single component solutions would indicate the existence and extent of the molecular interactions between the two proteins. To obtain isotherms of individual protein solutions, i.e., the equilibrium surface tension versus bulk solution concentration, the time evolution of the surface tension must be measured. ADSA-P was employed for measuring the surface tension as a function of time, i.e., dynamic surface tension (DST), of the protein aqueous solutions. Because of the change in surface tension after forming the solution drop, the shape or profile of the drop image was varying with time. The experiment would thus continue until the shape of the drop image became constant, i.e., a relatively constant surface tension value was obtained. In the experiment, the drop image was captured at 30- and 300-s intervals, respectively, for 2 and 5 h, for protein A and IgG aqueous solutions. The concentrations of the Protein A solution were 5 × 10−3, 5 × 10−2, 0.5, 10.0, 25.0, and 50.0 μM. The concentrations of the IgG solution were 6.67 × 10−3, 3.33 × 10−2, 0.167, 1.67, 3.33, 6.67, and 20.0 μM.

Dynamic surface tension of the mixed Protein A and IgG solution

To quantify the number of IgG molecules that can bind to one Protein A molecule, the DSTs of the mixtures of the two proteins were measured at a series of molar ratios. The IgG aqueous solution (0.3 ml) at a concentration of 1.67 μM was mixed with the Protein A aqueous solution (0.3 ml) at a series of varying concentrations: 5.0 × 10−3, 0.05, 0.10, 0.25, 0.334, 0.4175, 0.50, 0.556, 0.668, 0.75, 0.835, 1.20, 1.40, 1.67, 1.80, and 2.00 μM. This corresponded to the molar ratios of IgG to Protein A at 334:1, 33.4:1, 16.7:1, 6.68:1, 5:1, 4:1, 3.34:1, 3:1, 2.5:1, 2.23:1, 2:1, 1.4:1, 1.20:1, 1:1, 0.93:1, and 0.835:1. The dynamic surface tension measurement was conducted for 5 h, immediately (within 1 min) after the protein mixture was prepared.

Dynamic surface tension of the precipitate in solution

Inasmuch as the complex formed by Protein A and IgG would generate precipitates in the aqueous solution, to determine the effect of the precipitate presence on the surface tension measured from the mixed protein solution, we also performed the dynamic surface tension measurement for the solution containing the precipitate. An IgG solution (1.67 μM, 0.3 ml) was completely mixed with a Protein A solution (0.835 μM, 0.3 ml), with a molar ratio of 2:1. The mixture solution was allowed to stand for 4 h, and then centrifuged for 12 min at 5000 rpm. After removing the supernatant, the precipitate at the bottom of the container was taken out and resuspended in a fresh buffer (0.6 ml). The resulting suspension was used for the DST measurement as described above.

Mass balance analysis

To determine the concentration of the complex formed in the mixture of Protein A (0.835 μM) and IgG (1.67 μM), a 1:2 molar ratio, and to determine if any free protein molecules still existed in the mixture after the complex and precipitate formation, a mass balance analysis was performed for the amount of precipitate with respect to the original weights of the two proteins used in preparing the mixed solution. The sample solution was centrifuged and the supernatant was removed. The precipitate obtained might contain small amounts of water, e.g., due to humidity; thus, it was dried at 100°C for 1 h. The resulting dry precipitate was weighed using an electronic balance with a capacity of 52 g and a readability of 0.01 mg (Ohaus Analytical Plus Balance, Model AP250D, Ohaus Corporation, USA). The weight obtained was then converted into a molar concentration, and compared to the individual protein concentrations used for preparing the mixture.

UV-Absorbance measurement of the Protein A and IgG mixture

The absorbances of both pure Protein A (0.2 μM) and IgG (2 μM) solutions were measured in the wavelength range of 190–400 nm using an 8452A Diode Array Spectrophotometer (Hewlett-Packard). The variation in the UV absorbance was also measured for the mixed solution of Protein A and IgG, immediately after adding Protein A solution (0.1 ml, 2 μM) to IgG solution (0.9 ml, 2 μM), in the wavelength range of 190–400 nm. From these absorbance spectrums, the time evolution for complex and further precipitate formation could be estimated.

All the experiments mentioned above were run at least twice to obtain reproducible results.

THEORETICAL BACKGROUND

Here, we provide necessary theoretical backgrounds for analyzing molecular interactions from surface tension measurement. We will show the surface tension behavior in a mixture when the two molecules do not interact. The existence of molecular interactions is ascertained if this predicted surface tension behavior is found to be different from what was observed in experiment.

For a single component system, if the adsorbed molecules form a monolayer at the air/water (A/W) interface, the Langmuir adsorption isotherm can often be employed to describe the surface adsorption (Hansen, 1960). The Langmuir equation has the following form:

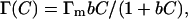graphic file with name M1.gif (1)

where b is the Langmuir adsorption isotherm parameter in L/mole, Γ is the surface adsorption at any time in mole/m2, Γm is the maximum surface excess concentration in mole/m2, and C is the bulk concentration in mole/L. For a dilute solution the Gibbs adsorption equation that relates the surface adsorption and surface tension can be employed, and a surface equation of state can be derived (Adamson and Gast, 1997):

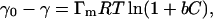graphic file with name M2.gif (2)

where γ0 and γ are the surface tensions of the solvent and the solution, respectively, in (mN/m); R is the universal gas constant; and T is the absolute temperature in K (Gao and Rosen, 1994). Eq. 2 can predict the equilibrium surface tension of the solution at small or moderate bulk concentrations.

When the system is not a single component solution but rather a binary mixture, then the situation is different. For example, if we consider a binary solution of A and B and also assume that the components do not interact with each other, then the following thermodynamic relations can be obtained (Adamson and Gast, 1997; Neumann et al., 1996):

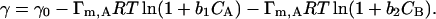graphic file with name M3.gif (3)

This equation can predict the mixture surface tension when assuming no molecular interactions between the two components. When the mixture equilibrium surface tension does not follow the above equation, then qualitatively we can infer the existence of molecular interactions. It is also noted that in Eq. 3 the presence of a second component always decreases the surface tension of the mixture; when this is not the case, molecular interactions must have occurred. On the other hand, when the surface tension is reduced upon an addition of a second component, it is not necessary that no molecular interactions have occurred. In the situations where the surface tension is reduced to a minimum as the concentration ratio between the two components is varied, the so-called surface tension synergism occurs (Siddiqui and Franses, 1996).

RESULTS AND DISCUSSION

Dynamic surface tension of individual protein solutions

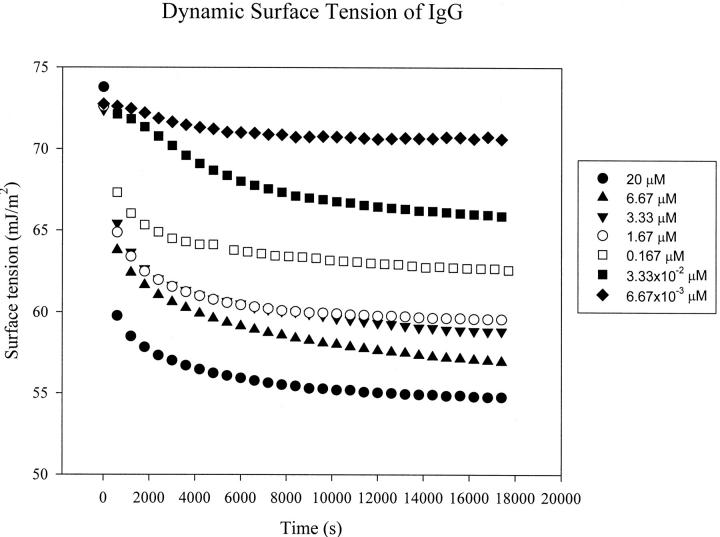
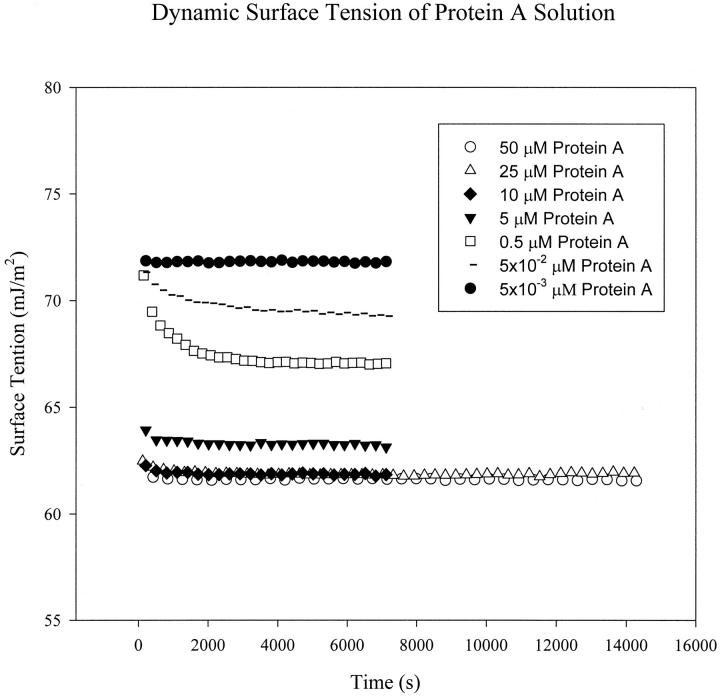
To study the interactions of Protein A and IgG using surface tension measurement, it is essential to determine the DST of the each protein solution first. The DSTs of Protein A and human serum IgG as a function of time at different concentrations are shown in Figs. 2 and 3, respectively. One can see that the surface tension decreases very quickly at the beginning for higher concentrations (starting at 0.167 μM for IgG and 0.5 μM for Protein A). The surface tension approaches a plateau after ∼1.5 h for IgG, and only 3 min for Protein A, which indicates that IgG takes a longer time than Protein A to reach adsorption equilibrium at the A/W interface.

FIGURE 2.

FIGURE 2

Open in a new tab

Dynamic surface tension (DST) of the IgG solution at bulk concentrations of 20 μM (•), 6.67 μM (▴), 3.33 μM (▾), 1.67 μM (○), 0.167 μM (□), 3.33 × 10−2 μM (▪), and 6.67 × 10−3 μM (♦). In each run, drop images were captured at 300-s intervals for 5 h.

FIGURE 3.

FIGURE 3

Open in a new tab

Dynamic surface tension of the Protein A solution at bulk concentrations of 50 μM (○), 25 μM (▵), 10 μM (♦), 5 μM (▾), 0.5 μM (□), 5.0 × 10−2 μM (−), and 5.0 × 10−3 μM (•). In each run, drop images were captured at 30- or 60-s intervals for 2 or 4 h.

For surface-active proteins, the general adsorption kinetics at the A/W interface may be considered to be a three-step process (MacRitchie and Alexander, 1963): 1) diffusion of solute molecules from bulk solution to the subsurface region; 2) adsorption of molecules from the subsurface to the A/W interface; and 3) conformational rearrangements of adsorbed protein molecules. The diffusion coefficient (D) of a macromolecule can be estimated using the Stokes-Einstein equation:

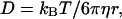graphic file with name M4.gif

where kB is the Boltzmann constant, T is the absolute temperature, η is the viscosity of the solvent, and r is the solute radius (McCammon and Harvey, 1987). In the equation above, diffusion coefficient is inversely proportional to the molecular size. For the present study, the molecule of IgG has a molecular weight of 150 kDa, which is much larger than that of Protein A of 42.0 kDa. Thus, the value of diffusion coefficient of IgG is much smaller than that of protein A (Tripp et al., 1995). This will result in a much slower first step of adsorption for IgG. Because of larger size, and possibly more complicated molecular chemical structure, IgG molecules may encounter a higher energy barrier in the second step of adsorption, compared with much smaller, and maybe more mobile, Protein A molecules. Therefore, the second step of adsorption can be significantly slower for IgG than for Protein A. Furthermore, larger molecules can take a longer time to complete reorientation and conformational changes after being adsorbed at the interface. It is possible that the IgG molecules take more time to rearrange themselves to an equilibrium state at the surface than the Protein A molecules. Considering all three kinetic steps for adsorption, it is reasonable to expect that IgG takes a longer time than Protein A to reach a surface tension plateau and approach adsorption equilibrium (Figs. 2 and 3).

In Fig. 2, induction times are observed for IgG at low concentrations (3.33 × 10−2 μM and 6.67 × 10−3 μM). Induction time is the time during which surface tension remains nearly equal to the pure solvent surface tension. At very low protein surface concentrations, the interface possesses the physicochemical properties of the solvent (buffer solution here), with an equilibrium surface tension of solvent (McCammon and Harvey, 1987). The solution surface tension will decrease from the pure solvent value only after a certain amount of solute molecules has adsorbed at the interface. For globular proteins adsorbing at the A/W interface, ∼50% of the close-packed monolayer surface concentration must be attained before the surface tension decreases significantly from the pure buffer surface tension (Song and Damodaran, 1991). At low concentrations, IgG molecules of large molecular size need a certain time to diffuse and adsorb to the surface from the bulk, to attain half of the monolayer surface concentration at the A/W interface. The induction times thus appear at low IgG concentrations. However, no induction time is observed for Protein A even at low concentrations (see Fig. 3). As protein A is a much smaller molecule compared with an IgG molecule, its relatively quick adsorption kinetics makes the surface concentration of protein A reach 50% of the monolayer surface concentration very fast. The surface tension thus decreases very quickly.

Equilibrium surface tension

As shown in Figs. 2 and 3, the adsorption of IgG and Protein A approximately approaches to equilibrium in 1.5 h and 3 min, respectively, but the true equilibrium has never been reached. To obtain equilibrium surface tension, methods of data analysis for DST must be used: Method A, the average of the last 10 values of DST data points; and Method B, extrapolation of the plot of γ versus 1/t1/2 (Cabrerizo-Vilchez et al., 1995). Method A is intuitive and easy to use. Method B is based on a transport-controlled mechanism, which asserts a linear relationship between γ and 1/t1/2 when the surface adsorption is approaching its equilibrium (Miller and Lunkenheimer, 1983). For applying Method B, the plots of γ versus 1/t1/2 for IgG and Protein A at different concentrations are plotted (not shown), respectively. The data at large time periods are fitted to a straight line by linear regression. Extrapolation to zero (i.e., t = ∞) provides an estimate of the Equilibrium Surface Tension (EST) (γe) (Miller and Kretzschmar, 1991).

The EST results obtained by Methods A and B are presented in Table 1. For Protein A, the equilibrium surface tension, γe, values at different concentrations obtained by the two methods are very close; whereas, for IgG, γe(A) > γe(B). This is because the obtained DST data of Protein A has almost reached the equilibrium within the experimental time, but not for IgG. Considering the theoretical basis of Method B, the present DST data may better be analyzed with the extrapolation method, and the extrapolated equilibrium surface tension will be used in generating the following adsorption isotherms.

TABLE 1.

Equilibrium surface tensions, γe (mJ/m2), of IgG and Protein A solutions as obtained by two methods: A) average of the last 10 data points and B) extrapolation

γe (mJ/m2)
IgG Conc. (μM) A B
20 54.72 53.31
6.67 56.94 55.06
3.33 58.82 57.18
1.67 59.54 58.07
0.167 62.56 61.42
3.33 × 10−2 65.86 63.46
6.67 × 10−3 71.69 69.85
γe (mJ/m2)
Protein A Conc. (μM) A B
50 61.59 61.59
25 61.72 61.75
10 61.79 61.77
5 63.02 62.96
0.5 66.99 66.14
5 × 10−2 69.27 69.16
5 × 10−3 71.79 71.81
Open in a new tab

Adsorption isotherms

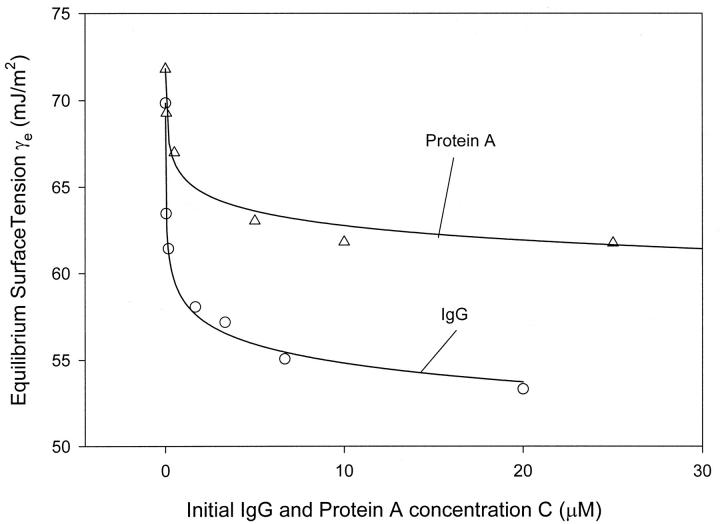
The EST (γe) of IgG and Protein A solutions at different concentrations obtained by the extrapolation method is plotted in Fig. 4. One can see that γe decreases with increasing bulk concentration for both Protein A and IgG solutions. However, the decease in γe becomes much slower and tends to a plateau after a critical concentration (∼1.67 μM for IgG, 5 μM for Protein A); it is similar to the surface tension behavior of surfactants where the critical concentration is a critical micelle concentration. Comparing the two isotherms in Fig. 4, one can also see that the surface tension of IgG is lower than the surface tension of Protein A at the same concentrations. It indicates that the surface activity of IgG is higher than that of Protein A at the air/water interface, and the IgG molecules may be more hydrophobic than those of Protein A.

FIGURE 4.

FIGURE 4

Open in a new tab

Isotherm of IgG (○) and Protein A (▵). The equilibrium surface tensions of the two protein solutions are obtained by the extrapolation method.

Suppose that the adsorption isotherms of the two proteins follow the Langmuir model; γ0, Γm and b values can be obtained by fitting Eq. (3) to the γe data using the least-squares fitting method. The radii of the two proteins can be calculated from Γm when assuming the two proteins to have a circular cross section at the A/W interface. The results are shown in Table 2. From the R2 values, it is seen that the adsorption data of both proteins fit the Langmuir model very well. The fitted theoretical values of the surface tension of the buffer, γ0, are very close to the experimentally measured one (73.37 mN/m). The fitted radius of Protein A molecule is 1.03 nm; this is reasonable inasmuch as, from a molecular modeling, the dimension of 1.25 nm can be estimated for Protein A (Clark, 1996). The fitted radius of IgG molecule (0.91 nm), however, is smaller than that reported in the literature (5.5 nm for IgG; Narita et al., 1999). This is probably due to the orientation of IgG molecules at the A/W interface. Buijs et al. (1995) reported that IgG molecules adsorb mainly in an end-on orientation at hydrophobic surfaces with Fc fragment toward the hydrophobic surface. For our A/W interface, air can be considered to be hydrophobic. The IgG molecules may take such an orientation that Fc fragments stretch out into the air, and Fab arms stay in the bulk solution. This arrangement of the IgG molecule would lead to a much smaller adsorption area at the interface.

TABLE 2.

Values of the equilibrium surface adsorption parameters* for IgG and Protein A calculated according to Eq. 3

γ0 (mN/m) Γm (mol/m2) A (nm2) r (nm) B (L/mol) R2
IgG 73.31 6.45 × 10−7 2.57 0.91 1.17 × 1010 0.9945
Protein A 73.43 4.96 × 10−7 3.32 1.03 7.58 × 108 0.9784
Open in a new tab
Γm is the maximum excess concentration of protein molecules at the surface; A refers to the area taken by one molecule at the A/W interface; and r is the radius of the assumed circular cross section of the molecule at the interface, calculated via the following equation:
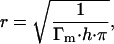graphic file with name M5.gif
where h is the Avogadro constant in 6.023 × 1023/mol, and π is a constant of 3.14.

The interaction between IgG and Protein A—dynamic surface tension analysis

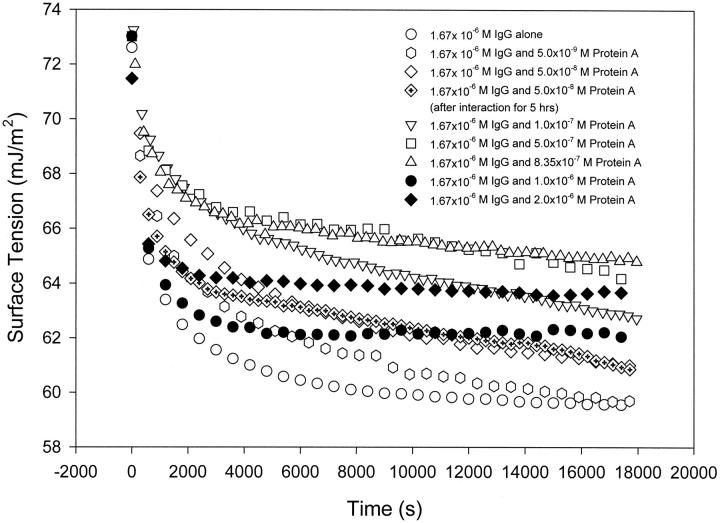
To determine the interaction and binding ratio of IgG to Protein A, dynamic surface tension of the mixture of IgG and Protein A at different concentration ratios was measured. From Fig. 5, we can see that the dynamic surface tension of pure IgG solution reaches equilibrium, or the region where the surface tension varies only slightly, on the order of hours. The addition of Protein A into the IgG solution makes the surface tension increased over the entire period of the measurement. It is noted that the highest surface tension occurs when the molecular ratio of Protein A to IgG in solution is 1:2, and a further increase in Protein A concentration leads to a reduction in surface tension. When the molecular ratio of Protein A to IgG is less than 1:2, the shape of the dynamic surface tension curves is similar to that of pure IgG solution. However, when the ratio increases to more than 1:2, the shape is similar to that of pure Protein A solution (see Fig. 3), where the surface tension has a rapid initial drop and quickly reaches a plateau on the order of minutes, and certainly less than an hour.

FIGURE 5.

FIGURE 5

Open in a new tab

Dynamic surface tensions of the mixture of IgG and Protein A solutions. In the mixture, the concentration of IgG is fixed at 1.67 × 10−6 M, and the concentration of Protein A is 5.0 × 10−3 , 0.05, 0.10, 0.50, 0.835, 1.0, and 2.0 μM, which correspond to molar ratios of Protein A to IgG at 1:334, 1:33.4, 1:16.7, 1:3.34, 1:2, 1:1.67, and 1:0.835, respectively. The dynamic surface tension measurements started immediately after mixing, and experimental duration was 5 h. It is noted that the highest surface tension is observed at the molar ratio of Protein A to IgG of ∼1:2.

These results indicate that the mixture resembles the pure IgG solution when the molecular ratio of the two proteins (Protein A/IgG) is less than 1:2, and resembles the pure Protein A solution when the ratio increases to more than 1:2. To explain these observations, we may suppose that Protein A and IgG interact with each other upon mixing in solution; at concentration ratios less than 1:2, almost all Protein A has bound to IgG, but there are excess IgG molecules left in the mixture. It is these unbound or free IgG molecules that are surface active and affect the surface tension of the mixture. This would make the DST of the mixture similar to that of the pure IgG solution. When the concentration or molecular ratio of Protein A to IgG is more than 1:2 in solution, Protein A molecules are excess; that is, nearly all of the IgG molecules have bound to Protein A molecules, but there are still some free Protein A molecules left in the mixture. This would result in the DST of the mixture being similar to that of pure Protein A solution. From these arguments, it is also seen that the 1:2 ratio between Protein A and IgG should represent a special characteristic for the binding between the two proteins (see below).

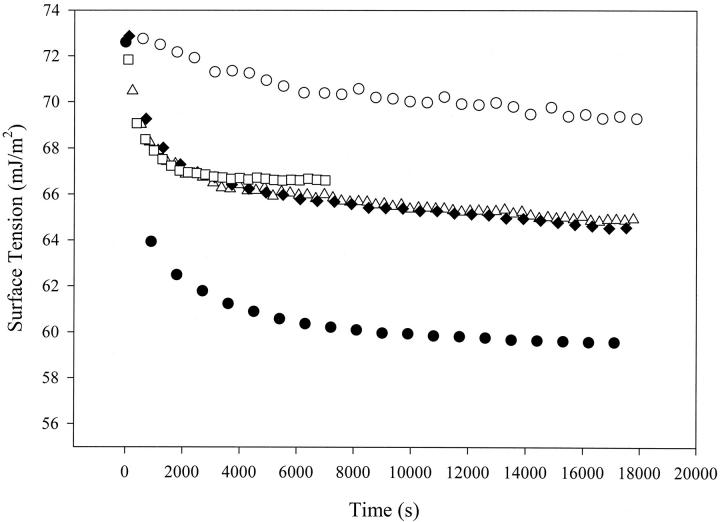
In the above discussion, it is assumed that the complex formed by binding between Protein A and IgG in solution does not contribute to the surface tension variation; only those free proteins, in their monomer form, affect the surface tension behavior of the mixture. To confirm this point, the DST of the complex particles or precipitates formed by Protein A (0.835 μM) and IgG (1.67 μM) at the special 1:2 molecular ratio was measured (see the Materials and Methods section). It is plotted together with the DSTs of the mixture of Protein A–IgG solution at the 1:2 ratio, the supernatant of the Protein–IgG mixture after centrifuging and removing the precipitates, pure IgG and pure Protein A solutions (Fig. 6). One can see that the precipitates exhibit a much higher surface tension and hence much lower surface activity than IgG, Protein A, or even the mixture of the two proteins. The DST of the supernatant is very close to that of the Protein A–IgG mixture. This indicates that the Protein A–IgG complex particles or precipitates make little contribution to the surface tension of the mixture. The surface activity in the mixture at the 1:2 molar ratio of Protein A to IgG is due to the fact that there are still some free single molecules in the mixture after protein binding.

FIGURE 6.

FIGURE 6

Open in a new tab

Comparison of the dynamic surface tensions of IgG-Protein A complex, IgG-Protein A mixture, pure IgG, and pure Protein A. ○, complex formed by 1.67 μM IgG and 8.35 μM Protein A; ▵, mixture of 1.67 μM IgG with 8.35 μM Protein A; ♦, supernatant of the above mixture after centrifuge treatment; •, 1.67 μM pure IgG; and ▪, 0.835 μM pure Protein A. The surface tension of the IgG-Protein A complex is clearly the highest, which indicates that this complex has little surface activity. The roughly equal surface tensions between the mixture and the supernatant indicate that the surface tension is essentially determined by soluble protein molecules, which are believed to be the free Protein A and IgG molecules left in solution after the binding reaction.

The interaction between IgG and Protein A—equilibrium surface tension analysis

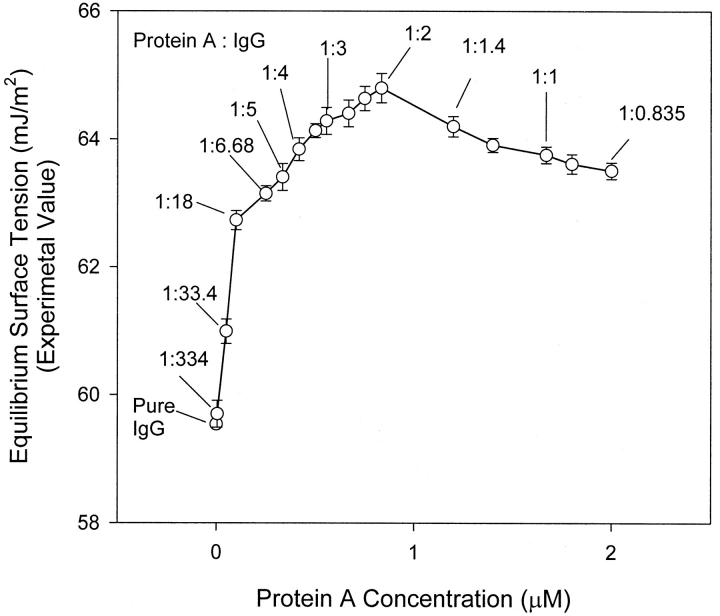
To confirm the existence of molecular interactions and further determine the molecular binding ratio between Protein A and IgG, the EST of the mixture at a fixed IgG concentration (1.67 μM) but different Protein A concentrations, i.e., varying molar ratios of protein A to IgG is plotted in Fig. 7. When assuming no interaction between Protein A and IgG, the EST of the mixture can be calculated using Eq. 3 (see the Theory section). We can see that the experimental EST of the mixture is higher than the theoretical one over the entire range of concentrations. The change in experimental EST with the Protein A concentration also shows a different trend from that of Eq. 3. Therefore, the assumption of no interaction is invalid, i.e., one must conclude that molecular interactions occur between Protein A and IgG in solution.

FIGURE 7.

FIGURE 7

Open in a new tab

The effect of Protein A concentration on the equilibrium surface tension of the mixture containing fixed IgG concentration of 1.67 μM and variable concentrations of Protein A. It is noted that the equilibrium surface tension reaches a maximum when the molecular ratio of Protein A to IgG is 1:2 in solution. This indicates that the maximum binding ratio or capacity is at 1:2 between this ligand–ligate pair.

In Fig. 7, the experimental EST of the two-protein mixture increases with increasing Protein A concentration from 0 to 0.835 μM, which corresponds to a 1:2 molar ratio of Protein A to IgG. With a further increase in Protein A concentration, the experimental EST drops down. This is a strong indication that the molecular binding ratio between Protein A and IgG is 1:2.

From the surface tension measurement of the ProteinA–IgG complex precipitates, we know that the complex particles do not affect the surface tension of the mixture; this surface tension is mainly due to the presence of unbound protein molecules in solution. When the protein A concentration is increased in the mixture, more Protein A–IgG complex will form; as a result, less free IgG molecules will be left in the mixture and hence result in an increase in EST. The EST reaches a maximum when the molar ratio of Protein A to IgG at 1:2 (0.835 μM Protein A to 1.67 μM IgG). This indicates that only at the 1:2 ratio of Protein A to IgG, the amount of free proteins left in the mixture is the least. In other words, the maximum binding between Protein A and IgG takes place at the 1:2 molar ratio. In should be noted that the EST of the mixed protein A and IgG solution at the 1:2 ratio is lower than that of the complex precipitates formed by Protein A and IgG at the 1:2 ratio (see Figs. 6 and 7). This indicates that there are still a small number of free proteins in the mixture even at the maximum binding ratio. When the concentration ratio between Protein A and IgG is over 1:2, no more complex can form even with a further increase in Protein A concentration. Excess free Protein A molecules exist in solution and cause the surface tension of mixture to decrease.

It should also be noted that the molecular binding ratio of 1:2 determined above is close to that reported in some of the literature (Sjöquist et al., 1972; Deisenhofer, 1981), and is consistent with that suggested in the specification sheet of the Protein A provided by the supplier (ProZyme Co.).

It is worth noting that the current surface tension method requires small amounts of sample solutions; a minimum volume can be of the order of 1 μl (a volume range was 0.02–0.002 ml for the present experiments). In contrast, the best fluorescence spectrophotometer requires a minimum sample volume of 0.6 ml in a standard 10 mm cell; even a fluorescence microplate reader needs at least 0.2 ml of sample solution. The efficient use of the sample is particularly beneficial for the study of many expensive biological samples, which may be difficult to obtain in large quantities.

Another important feature of the surface tension probe is its high sensitivity. From Figs. 2 and 3, one can see that noticeable changes in dynamic surface tension occur with both protein solutions at such low concentrations as nanomol/L (1.67 nmol/L for IgG and 5 nmol/L for Protein A solutions). One can also see from Fig. 5 that surface tension changes of the mixture of the two proteins are still detectable even when the Protein A concentration is 5 nmol/L. The sensitivity of the surface tension method can reach a nanomolar level, which is comparable to some of the best fluorescence methods (http://www.moleculardevices.com/pages/max_bib5.html#protein-quant; http://www.turnerbiosystems.com/t2/doc/appnotes/998_2675.html).

Mass balance analysis

To confirm the binding ratio obtained above, the precipitates of the complex formed in the mixed solution of Protein A (0.835 μM) and IgG (1.67 μM) were dried after removing the supernatant. The dried complex particles were weighed for the calculation of the concentration of the complex precipitates. If two IgG molecules bind with one Protein A molecule to form a complex with a molecular weight of 342,000 (=2 × 150,000 + 42,000), the concentration of the complex of 0.756 μM is obtained. Theoretically, if Protein A binds to IgG at a 1:2 molar ratio, the concentration of the complex should be close to that of Protein A, i.e., 0.835 μM at its maximum. The difference in complex concentration indicates that a certain amount of proteins could still be left in solution after centrifuging.

As stated before, it is most likely that some free proteins are left in the mixture, even with the concentration ratio at the maximum binding capacity of 1:2. The surface tension caused by the free proteins left in the mixture should be the same as that of the supernatant after removing the complex precipitates. As shown in Fig. 6, the supernatant has an EST of 64.4 mJ/m2. On the other hand, our recent investigation reveals that the surface tension of a mixture, in which the components have interactions with each other, is determined by the more surface active component (M. E. Biswas, C. Keyes, J. Duhamel, and P. Chen, unpublished data). Therefore, the surface tension of the supernatant, which should contain both Protein A and IgG, is mainly contributed by IgG. From the adsorption isotherm, an IgG concentration of 0.072 μM corresponds to the EST of 64.4 mJ/m2. Thus, the concentration of Protein A in the supernatant is half that of IgG and equals 0.036 μM. Adding 0.036 μM to 0.756 μM, a total concentration of 0.822 μM is obtained, which is reasonably close to the original concentration of Protein A (0.835 μM). Therefore, the mass balance analysis supports the earlier conclusion that the molar binding ratio between Protein A and IgG is 1:2.

The fact that a majority of the proteins formed the complex in the mixture indicates a large affinity constant, kd/ka, with kd being the dissociation rate constant and ka being the association rate constant. This is in agreement with a reported value (http://www.affinity-sensors.com/pdf/appnotes/APPNOTES2-1.PDF) from a kinetics study, where the overall affinity constant was found to be 1.62 × 10−9 M upon assuming pseudo-first-order conditions. Of course, based on the determined molecular binding ratio of 1:2 between Protein A and IgG, it is plausible to assume a second-order kinetics with respect to IgG. This reported value nonetheless supports the notion that a majority of Protein A and IgG would bind together in solution.

It should be noted that the current surface tension approach cannot determine the affinity/binding constant of a pair of proteins precisely if they do not have distinct surface activity and hence surface tension values. From our data, the equilibrium surface tensions of Protein A and IgG are all within a relatively small range between 55 and 60 mJ/m2; this makes it difficult to generate a binding isotherm for calculating the binding constant. We have since worked with another protein–ligand pair, bovine serum albumin (BSA) and 5-dimethylamino-1-naphthalene sulfonic acid hydrate (DNS); in this case, BSA is surface active at the A/W interface whereas DNS has little surface activity. After plotting the equilibrium surface tension values at different concentration combinations, both molecular binding ratio and affinity constant may be extracted through a kinetics analysis for the BSA–DNS system (Biswas et al., 2002).

It is also worth noting that the present method is demonstrated to be useful only in determining the total number of binding sites or the binding ratio between the two molecules, and the detailed structural information on the binding sites cannot be extracted readily from the surface tension data.

UV spectrum of IgG–Protein A mixture

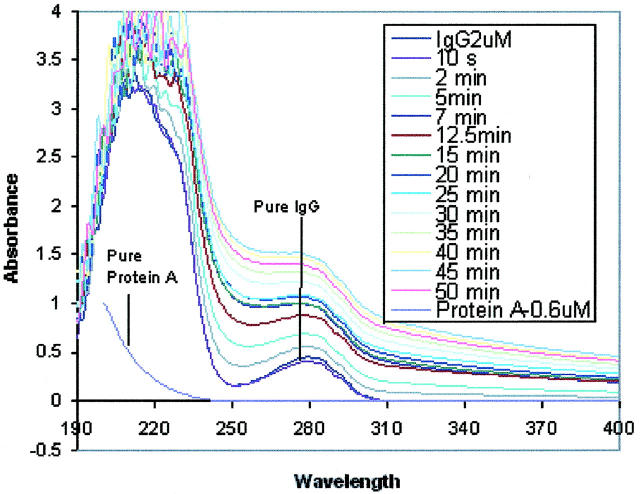
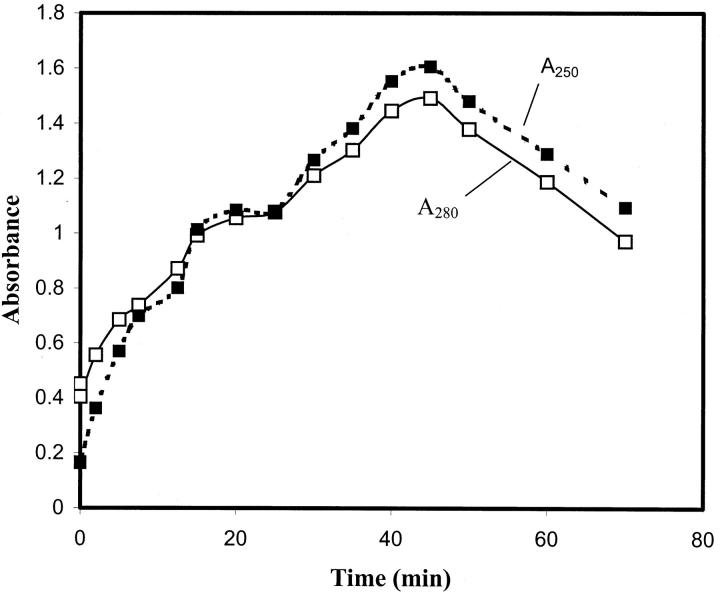
To further confirm the formation of the protein complex and its precipitates, the light absorbance experiment was conducted. In Fig. 8, the UV spectrums of the pure Protein A and IgG solutions, as well as the mixture of Protein A and IgG, are recorded in the wavelength range of 190–400 nm. One can see that the pure IgG solution (2 μM) exhibits an absorbance peak at 280 nm, which is the characteristic peak of a protein containing tryptophan residues. In contrast, the absorbance of the pure Protein A solution (0.2 μM) at 280 nm is nonexistent because Protein A does not contain tryptophan residues (Nardella et al., 1985). After mixing the two proteins in solution, the absorbance spectrum becomes time-dependent. The absorbance of the mixed protein solution declines a little immediately after adding the Protein A solution into the IgG solution (see Fig. 8, spectrum at 10 s). This is due to the instantaneous dilution of the IgG solution. Then, the absorbance starts to increase, and reaches its peak at 45 min; afterwards, it decreases with time (Fig. 9). During this period of absorbance variations, the mixed solution was first becoming cloudy, and small precipitates were observed visually, which was not the case with either of the pure protein solutions. Then, the mixed solution turned clear again with diminishing deposition of the precipitates.

FIGURE 8.

FIGURE 8

Open in a new tab

The change in UV absorption of IgG and Protein A solutions due to molecular interactions with each other. The absorbances of both pure Protein A (0.2 μM) and IgG (2 μM) solutions were measured in the wavelength range of 190–400 nm. The absorbance change with time of the mixed solution of Protein A with IgG was recorded after adding Protein A solution (0.1 ml, 2 μM) to IgG solution (0.9 ml, 2 μM) in the same wavelength range.

FIGURE 9.

FIGURE 9

Open in a new tab

Changes with time in the absorbance of the mixed solution containing 2 μM IgG (1 ml) and 2 μM Protein A (0.1 ml) at two wavelengths: 280 and 250 nm. It is noted that the absorbance peak occurs at ∼45 min.

The formation of precipitates indicates that the two proteins reacted with each other after mixing and formed complexes. The Protein A and IgG complexes were likely to aggregate into much larger precipitates, which were observed to deposit to the bottom of the glass container. That is, molecular interactions between Protein A and IgG must have occurred in solution, which corroborates the conclusion from the surface tension measurements.

The change in absorbance spectrum of the mixed solution (Fig. 9) can be explained with the complex formation and deposition of the precipitates: The complexes and their aggregates in solution would scatter the incoming light, and this would result in a net effect of increase in absorbance. The deposition of the complex aggregates, or precipitates, to the bottom of the sample container would, on the other hand, make the solution clear, and hence result in less light scattering and a net effect of decrease in absorbance, as measured by the spectrophotometer. When the two proteins were first mixed in solution, the rate of Protein A and IgG complex formation and aggregation was higher than that of the precipitation. Therefore, an increase in absorbance was observed. Such an increase reached a maximum at 45 min (Fig. 9) when the overall rate of complex aggregate formation was equal to the precipitation rate. After 45 min, the precipitation rate became larger than the complex formation rate, and this would result in a decease in absorbance.

It is important to note that the absorbance maximum occurred at 45 min; this indicates that the Protein A and IgG complex aggregate formation is a relatively fast process. Certainly, during the several hours of the surface tension measurements, the Protein A should have more than sufficient time to bind with IgG in solution. Thus, the time-dependent surface tension measured at late stages of the experiment should not be affected by the complex formation; rather, it is due to the individual protein surface adsorption and conformational changes, which is consistent with the earlier dynamic surface tension analysis.

CONCLUSIONS

A new method based on surface tension measurement has been developed for detecting molecular interactions; it can quantify molecular binding ratios (or capacities) between the interacting species. This method complements conventional approaches by being definite in determining molecular binding and flexible in sample preparation. For an important pair of biological ligand and ligate, Protein A and IgG, the existence of molecular interactions and the binding ratio of 1:2 have been determined unequivocally with the proposed surface tension method. These results have also been confirmed/supported by a mass balance calculation and spectrophotometry experiment.

In addition, through the dynamic surface tension measurements of Protein A and IgG aqueous solutions separately, surface adsorption isotherms have been established at room temperature. The results show that the Langmuir isotherm equation is a good approximation of describing the adsorption for both proteins at the air/water interface.

Acknowledgments

The authors are thankful to Dr. Jean Duhamel for his kind help on the UV-spectrum test.

The work was supported financially by the Natural Sciences and Engineering Research Council of Canada and the Premier's Research Excellence Award.

References

  1. Adamson, A. W., and A. P. Gast. 1997. Physical Chemistry of Surfaces. John Wiley & Sons, Inc., New York.
  2. Anderson, S. R., and G. Weber. 1969. Fluorescence polarization of the complexes of 1-anilino-8-naphthalenesulfonate with bovine serum albumin. Evidence for preferential orientation of the ligand. Biochemistry. 8:371–377. [DOI] [PubMed] [Google Scholar]
  3. Bjorklund, M., and M. T. Hearn. 1997. Characterisation of silica-based heparin affinity sorbents from equilibrium binding studies on plasma fractions containing thrombin. J. Chromatogr. A. 762:113–133. [DOI] [PubMed] [Google Scholar]
  4. Boyle, M. D. P., E. L. Faulmann, and D. W. Metzger. 1993. Applications of bacterial immunoglobulin-binding proteins to the purification of immunoglobulins. In Molecular Interactions in Bioseparations. T. T. Ngo, editor. Plenum Press, New York. 91–112.
  5. Boyle, M. D. P., and K. J. Reis. 1987. Bacterial Fc receptors. Biotechnology. 5:697–703. [Google Scholar]
  6. Buijs, J. J., W. T. Lichtenbelt, W. Norde, and J. Lyklema. 1995. Adsorption of monoclonal IgGs and their F(ab′)2 fragments onto polymeric surfaces. Colloids Surfaces B. 5:11–23. [Google Scholar]
  7. Cabrerizo-Vilchez, M. A., Z. Policova, D. Y. Kwok, P. Chen, and A. W. Neumann. 1995. The temperature dependence of the interfacial tension of aqueous human albumin solution/decane. Colloids Surfaces B. 5:1–9. [Google Scholar]
  8. Caffrey, M. 2001. Model for the structure of the HIV gp41 ectodomain: insight into the intermolecular interactions of the gp41 loop. Biochim. Biophys. Acta. 1536:116–122. [DOI] [PubMed] [Google Scholar]
  9. Chen, P. Z., C. R. Policova, C. R. Pace-Asciak, and A. W. Neumann. 1999. Study of binding of 12(S)-Hydroxy-5(Z),8(Z),10(E),14(Z)-eicosatetraenoic acid to bovine serum albumin using dynamic surface tension measurements. J. Pharma. Sci. 88:1293–1298. [DOI] [PubMed] [Google Scholar]
  10. Chen, P., Z. Policova, C. R. Pace-Asciak, P. M. Demin, and A. W. Neumann. 1996a. Dynamic surface tension responses to surface area change of mixed solutions of a Protein And small or medium-sized organic molecules. Colloid surfaces A. Physicochem. Eng. Aspects. 114:99–111. [Google Scholar]
  11. Chen, P., S. Lahooti, Z. Policova, M. A. Cabrerizo-Vilchez, and A. W. Neumann. 1996b. Concentration dependence of the film pressure of human serum albumin at the water/decane interface. Colloids Surf. B. 6:279–289. [Google Scholar]
  12. Clark, M. 1996. http://www.path.cam.ac.uk/∼mrc7/functions/fcrnpa.jpg.
  13. Deisenhofer, J. 1981. Crystallographic refinement and atomic models of a human Fc fragment and its complex with fragment B of Protein A from Staphylococcus aureus at 2.9- and 2.8-A resolution. Biochemistry. 20:2361–2370. [PubMed] [Google Scholar]
  14. del Rio, O. I., and A. W. Neumann. 1997. Axisymmetric drop shape analysis computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. J. Colloid Interface Sci. 196:136–147. [DOI] [PubMed] [Google Scholar]
  15. Gao, T., and M. J. Rosen. 1994. Dynamic surface tension of aqueous surfactant solutions. 6. Compounds containing two hydrophilic head groups and two or three hydrophobic groups and their mixtures with other surfactants. J. Am. Oil Chem. Soc. 71:771–776. [Google Scholar]
  16. Gee, K. R., W.-C. Sun, M. K. Bhalgat, R. H. Upson, D. H. Klaubert, K. A. Latham, and R. P. Haugland. 1999. Fluorogenic substrates based on fluorinated umbelliferones for continuous assays of phosphatases and β-galactosidases. Anal. Biochem. 273:41–48. [DOI] [PubMed] [Google Scholar]
  17. Hansen, R. S. 1960. The theory of diffusion-controlled absorption kinetics with accompanying evaporation. J. Phys. Chem. 64:637–641. [Google Scholar]
  18. Hou, K. C., R. Zaniewski, and S. Roy. 1991. Protein A immobilized affinity cartridge for immunoglobulin purification. Biotechnol. Appl. Biochem. 13:257–268. [PubMed] [Google Scholar]
  19. Ikonomov, V., W. Samtleben, B. Schmidt, M. Blumenstein, and H. J. Gurland. 1992. Adsorption profile of commercially available adsorbents: an in vitro evaluation. Int. J. Art. Org. 15:312–319. [PubMed] [Google Scholar]
  20. Jayaraman, V., R. Keesey, and D. R. Madden. 2000. Ligand–protein interactions in the glutamate receptor. Biochemistry. 39:8693–8697. [DOI] [PubMed] [Google Scholar]
  21. Jia, L., L. Yang, H. Zou, Y. Zhang, J. Zhao, C. Fan, and L. Sha. 1999. Protein A tangential flow affinity cartridge for extracorporeal immunoadsorption therapy. Biomed. Chromatogr. 13:472–479. [DOI] [PubMed] [Google Scholar]
  22. Jones, J. V. 1990. Staphylococcal protein A as an extracorporeal immunoadsorbent: theoretical and practical considerations. Transfus. Sci. 11:153–159. [Google Scholar]
  23. Klein, E., E. Eichholz, F. Theimer, and D. Yeager. 1994. Chitosan modified sulphonated poly(ethersulfone) as a support for affinity separations. J. Membr. Sci. 95:199–210. [Google Scholar]
  24. Lee, C. H., P. Y. Um, and M. H. Park. 2001. Structure-function studies of human deoxyhypusine synthase: identification of amino acid residues critical for the binding of spermidine and NAD. Biochem. J. 355:841–849. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Lindmark, R., C. Biriell, and J. Sjoquist. 1981. Quantitation of specific IgG antibodies in rabbits by a solid-phase radioimmunoassay with 125I-Protein A from Staphylococcus aureus. Scandinav. J. Immunol. 14:409–420. [DOI] [PubMed] [Google Scholar]
  26. MacRitchie, F., and A. E. Alexander. 1963. Kinetics of adsorption of proteins at interfaces. I–III. J. Colloid Sci. 18:453–464. [Google Scholar]
  27. McCammon, J. A., and S. C. Harvey. 1987. Dynamics of Proteins and Nucleic Acids. Cambridge University Press, London. 26.
  28. McClure, R. J., and B. M. Craven. 1974. X-ray data for four crystalline forms of serum albumin. J. Mol. Biol. 83:551–555. [DOI] [PubMed] [Google Scholar]
  29. Merkel, R., R. Nassoy, A. Leung, K. Ritchie, and E. Evans. 1999. Energy landscapes of receptor-ligand bonds explored with dynamic force spectroscopy. Nature. 397:50–53. [DOI] [PubMed] [Google Scholar]
  30. Miller, R., and K. Lunkenheimer. 1983. On the determination of equilibrium surface tension values of surfactant solutions. Colloid Polym. Sci. 261:585–590. [Google Scholar]
  31. Miller, R., and G. Kretzschmar. 1991. Adsorption kinetics of surfactants at fluid interfaces. Adv. Colloid Interface Sci. 37:97–121. [Google Scholar]
  32. Náray-Szabó, G. 1997. Protein-ligand interactions. In Molecular Interactions: From van der Waals to Strongly Bound Complexes. S. Scheiner, editor. John Wiley & Sons, Inc., Chichester, MA. 336–350.
  33. Nardella, F. A., D. C. Teller, C. V. Barber, and M. Mannik. 1985. IgG rheumatoid factors and staphylococcal Protein A bind to a common molecular site on IgG. J. Exp. Med. 162:1811–1824. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Narita, T., H. Kitazato, J. Koshimura, K. Suzuki, M. Murata, and S. Ito. 1999. Effects of protein meals on the urinary excretion of various plasma proteins in healthy subjects. Nephron. 81:398–405. [DOI] [PubMed] [Google Scholar]
  35. Neumann, A. W., and J. K. Spelt. 1996. Applied Surface Thermodynamics. Marcel Dekker, New York.
  36. Paulsson, M., and P. Dejmek. 1992. Surface film pressure of β-lactoglobulin, α-lactalbumin and bovine serum albumin at the air/water interface studied by Wilhelmy plate and drop volume. J. Colloid Interface Sci. 150:394–403. [Google Scholar]
  37. Pramanik, A., P. Thyberg, and R. Rigler. 2000. Molecular interactions of peptides with phospholipid vesicle membranes as studied by fluorescence correlation spectroscopy. Chem. Phys. Lipids. 104:35–47. [DOI] [PubMed] [Google Scholar]
  38. Rarbach, M., U. Kettling, A. Koltermann, and M. Eigen. 2001. Dual-color fluorescence cross-correlation spectroscopy for monitoring the kinetics of enzyme-catalyzed reactions. Methods. 24:104–116. [DOI] [PubMed] [Google Scholar]
  39. Rotenberg, Y., L. Boruvka, and A. W. Neumann. 1983. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces. J. Colloid Interface Sci. 93:169–183. [Google Scholar]
  40. Siddiqui, F. A., and E. I. Franses. 1996. Surface tension and adsorption synergism for solutions of binary surfactants. Ind. Eng. Chem. Res. 35:3223–3232. [Google Scholar]
  41. Sjöholm, I. 1975. Protein A from Staphylococcus aureus. Spectropolarimetric and spectrophotometric studies. Eur. J. Biochem. 51:55–61. [DOI] [PubMed] [Google Scholar]
  42. Sjöquist, J., B. Meloun, and H. Hjelm. 1972. Protein A isolated from Staphylococcus aureus after digestion with lysostaphin. Eur. J. Biochem. 29:572–578. [DOI] [PubMed] [Google Scholar]
  43. Song, K. B., and S. Damodaran. 1991. Influence of electrostatic forces on the adsorption of succinylated β-lactoglobulin at the air-water interface. Langmuir. 7:737–742. [Google Scholar]
  44. Spector, A. A., K. John, and J. E. Fletcher. 1969. Binding of long-chain fatty acids to bovine serum albumin. J. Lipid Res. 10:56–57. [PubMed] [Google Scholar]
  45. Suttiprasit, P., V. Krisdhasima, and J. McGuire. 1992. The surface activity of α-lactalbumin, β-lactoglobulin, and bovine serum albumin. I. Surface tension measurements with single-component and mixed solutions. J. Colloid Interface Sci. 154:316–326. [Google Scholar]
  46. Takano, H., J. R. Kenseth, S.-S. Wong, J. C. O'Brien, and M. D. Porter. 1999. Chemical and biochemical analysis using scanning force microscopy. Chem. Rev. 99:2845–2890. [DOI] [PubMed] [Google Scholar]
  47. Tashiro, M., and G. T. Montelione. 1995. Structures of bacterial immunoglobulin-binding domains and their complexes with immunoglobulins. Curr. Opin. Struct. Biol. 5:471–481. [DOI] [PubMed] [Google Scholar]
  48. Tornberg, E. 1978. The application of the drop volume technique to measurements of the adsorption of proteins at interfaces. J. Colloid Interface Sci. 64:391–402. [Google Scholar]
  49. Tripp, B. C., J. J. Magda, and J. D. Andrade. 1995. Adsorption of globular proteins at the air/water interface as measured via dynamic surface tension: concentration dependence, mass-transfer considerations, and adsorption kinetics. J. Colloid Interface Sci. 173:16–27. [Google Scholar]
  50. Uhlén, M., B. Guss, B. Nilsson, S. Gatenbeck, L. Philipson, and M. Lindberg. 1984. Complete sequence of the staphylococcal gene encoding Protein A: a gene evolved through multiple duplications. J. Biol. Chem. 259:1695–1702. [PubMed] [Google Scholar]
  51. Vidal, M. A., and F. P. Conde. 1985. Alternative mechanism of Protein A-immunoglobulin interaction: the VH-associated reactivity of a monoclonal human IgM. J. Immunol. 135:1232–1238. [PubMed] [Google Scholar]
  52. Ward, A. J. I., and L. H. Regan. 1980. Pendant drop studies of adsorbed films of bovine serum albumin. I, II. Film compressibility at oil/water interfaces. J. Colloid Interface Sci. 78:385–400. [Google Scholar]
  53. Wu, J. J., D. R. Yarwood, Q. Pham, and M. A. Sills. 2000. Identification of a high-affinity anti-phosphoserine antibody for the development of a homogeneous fluorescence polarization assay of protein kinase C. J. Biomol. Screen. 5:23–30. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES