Relating Single-Molecule Measurements to Thermodynamics

Abstract

Measurements made on large ensembles of molecules are routinely interpreted using thermodynamics, but the normal rules of thermodynamics may not apply to measurements made on single molecules. Using a polymer stretching experiment as an example, it is shown that in the limit of a single, short molecule the outcome of experimental measurements may depend on which variables are held fixed and which are allowed to fluctuate. Thus an experiment in which the end-to-end distance of the polymer molecule is fixed and the tension fluctuates yields a different result than an experiment where the force is fixed and the end-to-end distance fluctuates. It is further shown that this difference is due to asymmetry in the distribution of end-to-end distances for a single molecule, and that the difference vanishes in the appropriate thermodynamic limit; that is, as the polymer molecule becomes long compared to its persistence length. Despite these differences, much of the thermodynamic formalism still applies on the single-molecule level if the thermodynamic free energies are replaced with appropriate potentials of mean force. The primary remaining differences are consequences of the fact that unlike the free energies, the potentials of mean force are not in general homogeneous functions of their variables. The basic thermodynamic concepts of an intensive or extensive quantity, and the thermodynamic relationships that follow from them, are therefore less useful for interpreting single-molecule experiments.

INTRODUCTION

Biological molecules have traditionally been studied in ensemble experiments, where large numbers are probed and analyzed simultaneously. Such experiments yield smoothly varying time and population averages, and can be rigorously interpreted using conventional thermodynamics and chemical kinetics. The picture that emerges represents mainly the states of highest probability within the population. Recently, however, researchers have begun to employ methods designed to study biomolecules one at a time. Such single-molecule experiments have been used, for example, to investigate the elastic behavior of single DNA polymers, to unfold protein and RNA molecules, to measure the forces associated with molecular recognition, to investigate the kinematics and dynamics of single-motor molecules, and to follow the catalysis of individual enzymes. Single-molecule measurements often do not yield smooth, averaged values: individual molecules are found in states far from the mean of the population, and their instantaneous dynamics display chaotic and seemingly random behavior. The presence of large fluctuations affects the interpretation of data collected in single molecules. In particular, it raises the question, “what is the relationship between single-molecule measurements and thermodynamic data from ensemble measurements on the same systems?” Here we consider this question in the context of a common single-molecule experiment, measurement of a force vs. extension curve as a polymer molecule is stretched. We show that by replacing the familiar thermodynamic potentials (e.g., Gibbs free energy or Helmholtz free energy) with appropriate potentials of mean force, most but not all familiar thermodynamic concepts have close analogs on the single-molecule level. The primary difference is that although the choice of statistical ensemble is irrelevant for macroscopic systems, it can have a profound effect on single-molecule systems. Thus, in contrast to macroscopic thermodynamic systems, the results of single-molecule experiments may depend on which variables are held fixed and which are allowed to fluctuate. Though these conclusions are reached by considering a particular experimental situation, the general ideas and conclusions hold for a wide variety of microscopic systems.

The mechanical extension of a single molecule

Consider a polymer molecule suspended between a fixed surface (a glass surface or a bead in a micropipette, for example) and a force sensor of some sort. The force sensor may be a bead in a laser trap, the flexible cantilever of an atomic force microscope, a bendable microneedle, etc. (Cluzel et al., 1996; Smith et al., 1996). The molecule may have a simple random coil structure, like a long DNA molecule, or may have a unique three-dimensional fold, like a globular protein. In the course of the experiment a force-extension curve will be measured. This can be done in either of two distinct idealized experiments:

1. In the ideal isometric experiment, the end-to-end distance is held absolutely fixed and the (fluctuating) force on the sensor is measured. For example, one end of the polymer is attached to a rigid support, and the other end is attached to a bead held in an optical trap. The position of the bead is controlled by a feedback loop that adjusts the trap center so as to cancel all fluctuations of the bead position. The separation x of the ends of the molecule is thus fixed and the force F applied by the molecule to the trapped bead fluctuates. This force is measured as a function of time, say, by recording the movements of the laser trap, or by measuring the corresponding photon momentum changes. The force-extension curve of the molecule is obtained by slowly varying (in small increments) the location of the trap center, and at each step averaging the force F over an appropriate time period. The result is a plot of mean force, 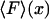, vs. the end-to-end separation, x, of the molecule.

2. In the ideal isotensional experiment, the force is held fixed and the end-to-end distance fluctuates. In the experimental setup above, the feedback loop would adjust the trap center so as to keep the displacement of the bead from the trap center at a fixed value, so the tension F in the molecule is constant. The end-to-end distance x fluctuates, and the force-extension curve is then the average end-to-end separation, 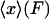, as a function of the applied tension F.

The functions 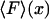and 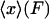also depend on temperature, pressure, and the composition and pH of the surrounding solution, but we will assume that these are held fixed. By inverting the graph of 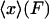one obtains a plot of fixed force vs. mean position, 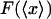, which is the closest equivalent to the force-extension curve, 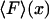, from the isometric experiment. When fluctuations are negligible, e.g., for long, flexible molecules, the two experiments yield identical results, but in the short molecule limit the results may differ.

The isometric experiment

Let us begin with the isometric experiment, which is slightly simpler than the isotensional one. Suppose that a positive value of F denotes a tensile applied force, i.e., a force that tends to stretch the molecule, whereas negative F represents compression. The quasi-static work 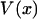performed on the molecule during the extension from 0 to x, i.e., the energy required to extend the molecule to a given value of x, is

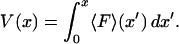(1)

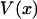is usually called the potential of mean force for the system at fixed x. Inasmuch as the experiment is carried out quasi-statically, 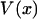is also the maximum reversible work for the process and, therefore, its magnitude is equal to the Gibbs free energy change of the molecule as a function of extension, x. Like 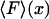, it is formally a function of the length of the polymer, L, as well as the external pressure, temperature, and mole numbers, V = V(x; L, P, T, n₁, n₂…), but these variables will be assumed constant and suppressed.

Inasmuch as the potential of mean force is a free energy, it is closely related to the probability (density), 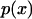, for observing the bead at position x along the line joining the ends of the polymer in the absence of an external force (Fig. 1:

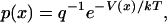(2)

where q is a normalization factor for the distribution. (Notice that 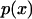is related to, but is not the same as, the distribution of end-to-end distances in a free polymer.)

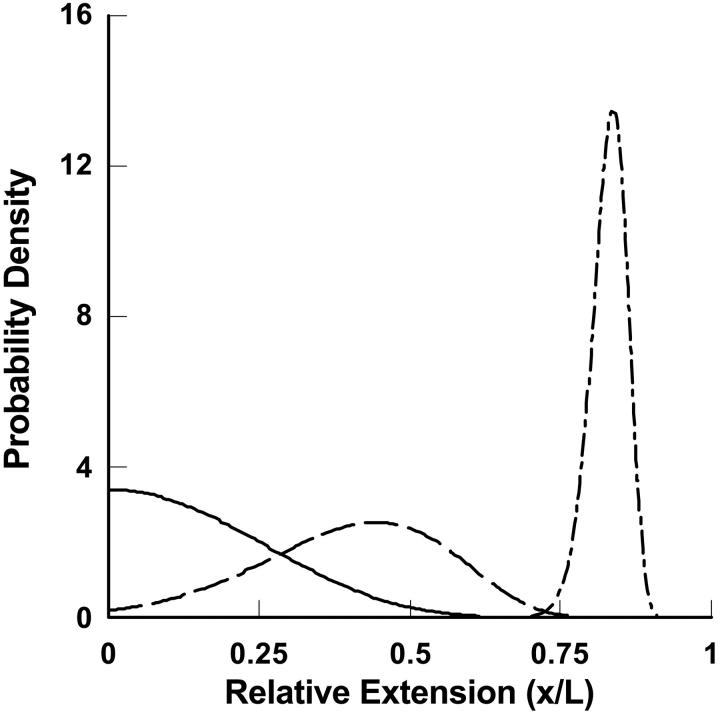
FIGURE 1.

Schematic plot of the probability distribution of the end-to-end distance of a long polymer molecule (contour length, L, persistence length, P = 10) along a particular direction, x, in the absence of an external force (F = 0, solid line), in the presence of a medium force (F = 10 kT/P, dashed line), and in the presence of a large force (F = 100 kT/P, dashed-dotted line). The distribution of end-to-end distances becomes increasingly narrow and asymmetric with increasing tension. The distribution is Gaussian only very near the probability maximum. At low extensions the curve rises more slowly than Gaussian and at high extensions it decays faster than Gaussian.

From an experimental point of view, the primary quantity is the mean force, 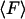, and the potential, V, is derived from it. But from a theoretical point of view energy is the more useful quantity. The relation between 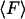and V can be written

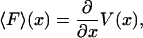(3)

which is identical in form to more familiar thermodynamic relationships such as 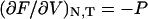, between pressure and Helmholtz free energy, F(N, V, T). For a microscopic, single-molecule system, the potential of mean force is the closest equivalent to a macroscopic thermodynamic free energy. However, unlike familiar thermodynamic variables such as volume, temperature, or mole numbers, the extension x is (in general) neither an extensive nor an intensive property, and the potential of mean force thus does not share all the properties of a macroscopic free energy (see below).

The isotensional experiment

The isotensional experiment can be understood in the same way as the isometric case, but the roles of the extension and force as fixed and fluctuating quantities are reversed. In the presence of a fixed external force, F, the energy of the molecule is

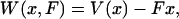(4)

where 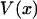is the potential of mean force for the isometric case, and Fx is the work done by the fixed external force in extending the molecule to length x. The measured mean extension, 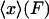, as a function of external force, F, is then

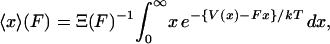(5)

where is the normalization factor, 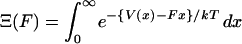. One may define the Gibbs free energy in the presence of an external force, 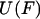, as

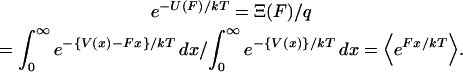(6)

Inasmuch as the potential of mean force, 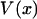, can be derived from the mean force, 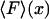, Eq. 6 is a relation between the results of the isometric and isotensional experiments.

From the definition of 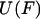it follows that

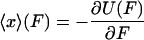(7)

and therefore,

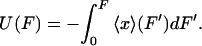(8)

Eqs. 7 and 8 are identical in form to Eqs. 3 and 1, respectively, except for the sign change. We will therefore refer to 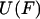as the potential of mean position. Importantly, Eq. 8 also shows that the potential of mean position, like the potential of mean force, can be calculated directly from experimental data.

Eq. 6 makes clear that the exponentials of 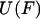and 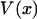are related by a Laplace transform (to within a constant of normalization),

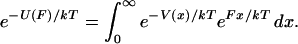(9)

This relation is exactly analogous to the relation between the partition functions in the canonical ensemble and in the grand canonical ensemble (with grand canonical free energy replacing U, the Gibbs free energy replacing V, the chemical potential replacing F, and mole number replacing x). The close analogy emphasizes the fact that a change from an isometric experiment to an isotensional experiment is really an opening of the system in the sense of allowing for all extensions x and hence broadening of the statistical-mechanical ensemble that describes the system.

Conditions for identity of isometric and isotensional force-extension curves: the thermodynamic limit

The results above show that isometric and isotensional experiments can (in general) lead to different results, but do not explicitly tell us how large the differences can be or when they may vanish altogether. In this section we will show i) that the difference between the isometric and isotensional cases can be understood as the difference between the average value of x, 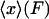, and the most probable value of the extension, x_mp(F), for the distribution of end-to-end distances of a molecule under tension, ii) that for small systems the difference between the isometric and isotensional cases vanishes only if the potential of mean force is quadratic in x, and iii) that the difference between isometric and isotensional cases vanishes when the molecule becomes long, that is, in the thermodynamic limit.

Consider an isotensional experiment with a fixed applied force F^*. The probability distribution p_F^*(x) for the end-to-end distance x of the molecule subject to F^* is, by Eq. 4,

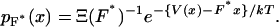(10)

The isotensional experiment yields 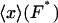, which is the average value of x for the distribution p_F^*(x) (Fig. 2). The most probable value x_mp of x for this distribution is a solution of the equation

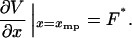(11)

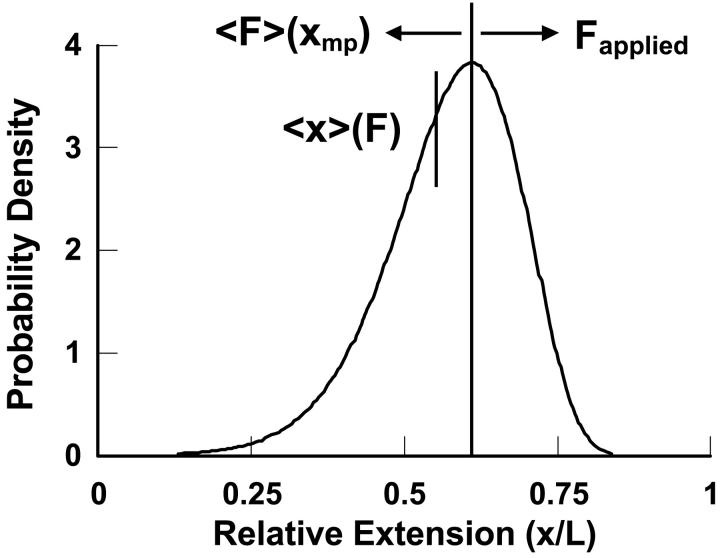
FIGURE 2.

Illustration of the physical origin of the difference between 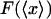and 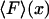. The curve is the distribution of end-to-end distances in the presence of fixed applied force F. At the most probable extension, x_mp, the mean chain tension, 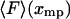, must balance the applied force, F. Hence the inverse of the most probable extension as a function of F, 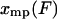, is equal to the mean force, .

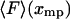We shall focus here on cases where, for each F^*, there is only one solution x_mp of Eq. 11, and hence V is a convex function of x. By comparing Eq. 3 and Eq. 11 we see that if an isometric experiment was conducted with the same molecule, then F^* would be the measured mean value of the force if the fixed extension was x_mp, i.e., 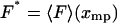. The plot of the most probable extension, x_mp, versus F^* in an isotensional experiment is therefore the inverse of the graph 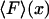of mean force versus extension for the isometric experiment. Therefore, the difference in the measured force-extension curves for the isotensional and isometric experiments performed with the same molecule is the difference between the mean 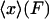and the most probable 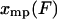values of the extension x for the distribution .

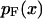It is not hard to show that the difference between isometric and isotensional experiments vanishes only when the force-extension curve is linear, that is, only when the molecule behaves as a Hookean spring. Eq. 10 implies

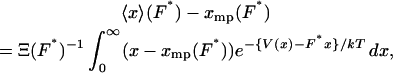(12)

which, if x_mp, instead of F, is taken as the independent parameter, is equivalent to

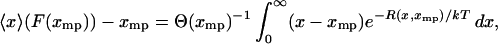(13)

where for each x_mp the function 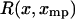is equal to the potential of mean force 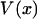minus its linear approximation at x^*, i.e.,

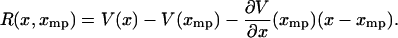(14)

From Eq. 13 it follows that if 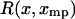is symmetric in the variable x about 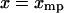, i.e., if

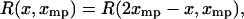(15)

then 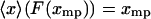. If the condition Eq. 15 holds for each 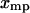, then 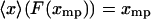for each 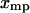, and hence 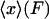equals 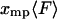for each F, which means that the isometric and isotensional force-extension curves are identical. It is easy to show that Eq. 15 is valid for each 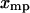only if 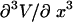is identically zero, i.e., only if 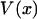is at most a quadratic function. In summary, the force-extension curves obtained from isometric and isotensional experiments are identical if and only if the potential of the mean force 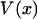is a quadratic polynomial in x, i.e., if the force-extension curves are linear.

Even if 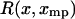is not symmetric, one can show that if the potential of mean force, 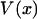, depends on the length L of the molecule in the right way, then the force-extension curves of isometric and isotensional experiments approach each other as the molecule becomes long. More precisely, suppose that 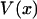is a convex function that is first order homogeneous in L, i.e., is such that 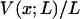is a function, say v, of 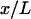only. Then 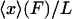approaches 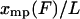, (i.e., 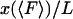) as the length L of the molecule approaches infinity.

Let ξ be the relative extension 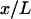. The lowest term in the Taylor expansion of 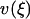about 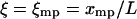is of even order. If the lowest term is quadratic, then

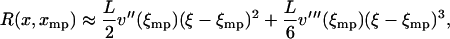(16)

with 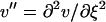, etc.

After substituting Eq. 16 into Eq. 13 and expanding the exponential of the cubic term about one has

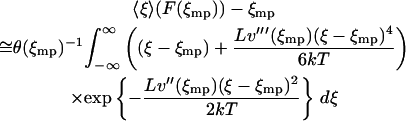(17)

with 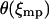the appropriate normalizer. The expansion of the integral in Eq. 13 into the one in Eq. 17 is justified when the standard deviation 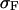of the probability distribution 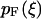is negligible compared to 1. Inasmuch as, in the limit of large L, 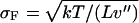, this expansion is justified when 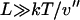. If V(x) is convex 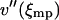is positive and the integral in Eq. 17 is finite. Evaluation of the integral yields

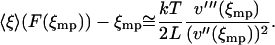(18)

Thus the difference between the average relative extension and the most probable relative extension approaches zero as L approaches infinity. It is a consequence of statistical thermodynamics that if the properties of the molecule are uniform along its length, then as the length of the molecule increases, the corresponding potential V approaches a homogeneous function of x. Therefore, if the potential of mean force V is a convex function of the extension x the isometric and isotensional force-extension curves approach each other as the length of the polymer approaches infinity.

This result is clearly a special case of the established notion that, in the thermodynamic limit, as the size of the system under consideration approaches infinity, the choice of ensemble is arbitrary. In other words, inasmuch as fluctuations are negligibly small, it does not matter which variables fluctuate, and only mean values are significant. In the formulas above, this limit comes about because as the molecule gets long, the function 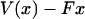has a deep narrow minimum for each value of F. Physically this means that there is little fluctuation about the most probable extension 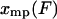, and the mean value of x, 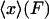, is approximately equal to 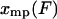. Also, the integral in Eq. 9 reduces to approximately , so the potential of mean position is related to the potential of mean force in the same way as two thermodynamic potentials:

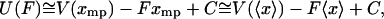(19)

where C is an additive constant that comes from the normalization in Eq. 9. This last equation is the analog of the standard thermodynamic relation between enthalpy and internal energy. In the thermodynamic limit then, 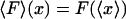, and the isometric and isotensional experiments yield the same result.

Calculations

When the system is small and the force-extension curve is nonlinear, i.e., its potential is not a quadratic function of the extension, in general the results of isometric and isotensional experiments will differ. Fig. 3, A–C, shows calculated functions 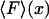and 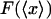versus the fractional extension, x/L, for polymer stretching experiments with three different molecular lengths. For these calculations the function 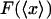was evaluated using a simplified statistical-mechanical model in which it is assumed that the perturbed configuration of the segment varies little from the straight configuration, and hence can be expanded in normal modes of vibration. This assumption limits the applicability of the model to cases where the extension x is close to L, i.e., to cases in which the molecule is nearly fully extended. Explicit evaluation of the partition function for the model yields

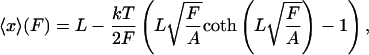(20)

where A is the bending elastic constant for the polymer, equal to the persistence length P multiplied by kT. P was taken to be the standard value for DNA, i.e., 50.0 nm in Fig. 3 (Bustamante et al., 1994). The asymptotic behavior of this last relation for large F is the same as the behavior of the relation proposed before for long DNA's (Bustamante et al., 1994; Marko and Siggia, 1995). For F = 0, however, Eq. 20 gives 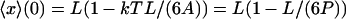, which is in accord with the result of Landau and Lifshitz (1958), and reflects the expectation that when L is of the order of the persistence length (or less), the average extension of a DNA segment should be nonzero even if no force is applied on the segment. The values of the function 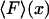were calculated by using Eq. 8 to find U(F), then applying a numerical inverse Laplace transform to Eq. 9 to obtain V(x), and then using Eq. 3. In this example the force in the isotensional experiment is always greater than the force in the isometric experiment at the same extension. The two curves approach each other when the DNA is at least a few persistence lengths, and are essentially indistinguishable when the DNA is about 10 persistence lengths, (not shown).

FIGURE 3.

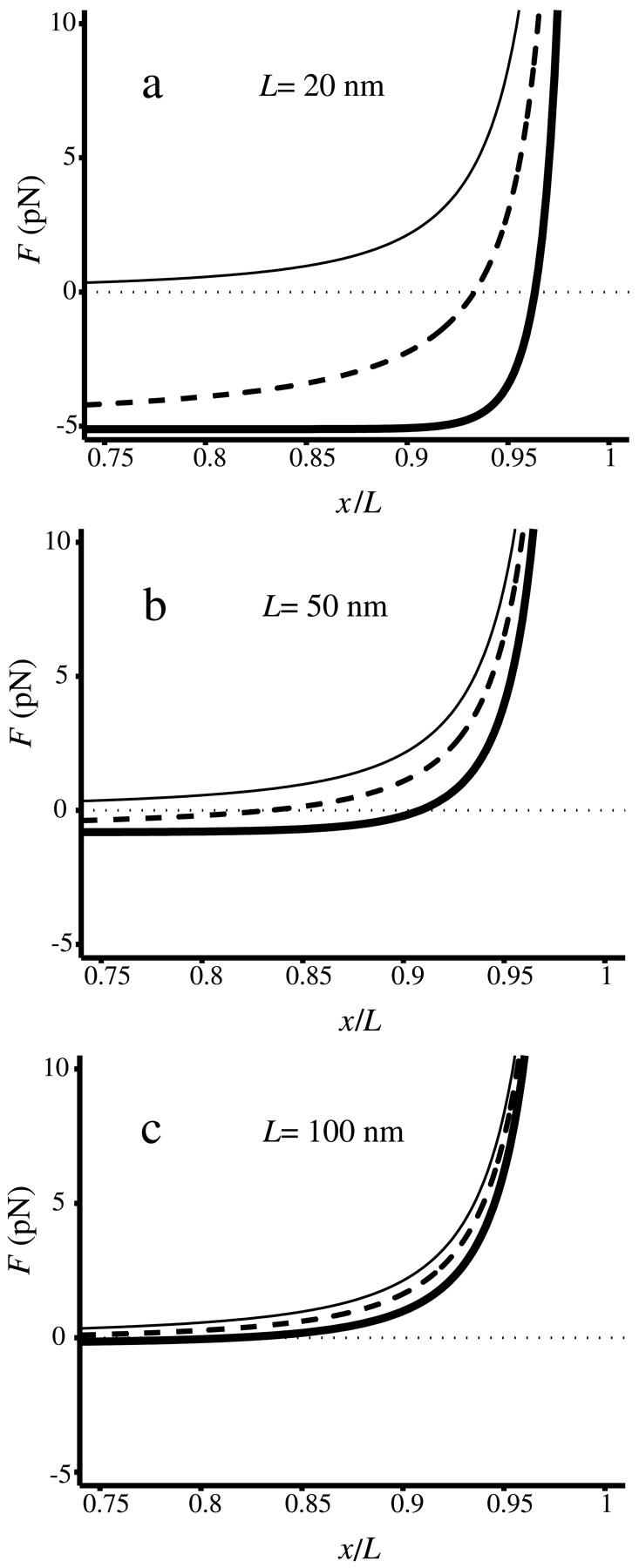
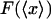vs. x/L (dark solid curves), and vs. 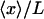(dashed curves), calculated for DNA molecules of three different lengths corresponding to (a) 20 nm (L/P = 0.4), (b) 50nm (L/P = 1), and (c) 100 nm (L/P = 2). In all cases a persistence length of 50 nm was assumed. The model used for these calculations is more accurate for values of x/L between 0.75 and 1.0. As is apparent in these examples, the 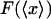and 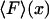curves approach each other as the molecule becomes larger and the fluctuations become correspondingly negligible.

In summary, when fluctuations are significant, all the measured characteristics of a single molecule will depend on the type of constraints used, and a model appropriate to the given experimental setup must be used to deduce values of material parameters for the molecule under consideration. For example, the elastic parameters of a DNA molecule can be found from the isometric force-extension curve, by fitting it to an appropriate model. But if the molecule is short it should not be modeled with Eq. 20, which is appropriate for the isotensional experiment. The correct approach would be to first transform Eq. 20 (or the equivalent relationship from another model) using Eq. 9 and then compare to the force-extension curve.

CONCLUSIONS

Thermostatistics in the single-molecule limit

Though the emphasis in this paper has been on polymer force-extension curves, the same basic conclusions apply, mutatis mutandis, to many other experiments. For example, in a recent set of experiments a DNA molecule was twisted by applying an external torque (Strick et al., 1996, 1998). If the DNA is short enough (a few torsional persistence lengths or less) experiments performed with fixed torque and fluctuating twist will differ from those with fixed twist and fluctuating torque.

The closest single-molecule analogs of the thermodynamic free energies are the potential of mean force, V(x), and potential of mean position, U(F). Both can be found directly from experiment, by integrating the appropriate force-extension curve, and, like the thermodynamic free energies, both potentials can be used to find the equilibrium properties of single-molecule systems as functions of appropriate mechanical and thermodynamic variables. For present purposes we have chosen to emphasize the mechanical relationships, e.g., between V(x) and 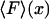, but if the single-molecule experiment is carried out at constant temperature and pressure, 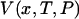is essentially a Gibbs free energy, and many “pure” thermodynamic relationships also hold. For example, if V is known as a function of T, then the entropy as a function of extension, x, is given by 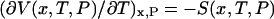. Likewise, if, say, a DNA molecule is stretched in the presence of an intercalator, then the corresponding chemical potential will depend on the extension of the DNA according to 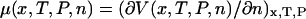, where n is the number of bound intercalator molecules. Similar relationships hold for the potential of mean position, U(F).

Thus the potentials V(x) and U(F) play a role in single-molecule thermostatistics similar to the free energies in ensemble thermodynamics. As pointed out earlier however, V(x) and U(F) need not be homogeneous functions of x or F, and so V(x) and U(F) do not (in general) satisfy the numerous thermodynamic relationships that depend on the intensivity and extensivity of thermodynamic parameters. For example, in a macroscopic system the thermodynamic Gibbs free energy, G, is a first-order homogeneous function of mole numbers, n, and therefore satisfies the Euler relation, 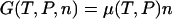. Similarly, because the thermodynamic internal energy is first-order homogeneous in S, V, and n, the thermodynamic parameters satisfy the Gibbs-Duhem relation, 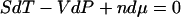. Neither of these relationships holds in general for a single-molecule system. In particular, there is no generally valid “mechanical” Gibbs-Duhem relationship such as 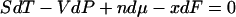, inasmuch as this would require V(x) to be first order homogeneous in x. These caveats may also apply to classical thermodynamic variables like mole number, n: in the single-molecule limit the appropriate thermostatistical potential need not be first-order homogeneous, and neither the Euler relation nor the Gibbs-Duhem equation, nor relationships that depend on them, need hold.