Limiting Frequency of the Cochlear Amplifier Based on Electromotility of Outer Hair Cells

Abstract

Outer hair cells are the critical element for the sensitivity and sharpness of frequency selectivity of the ear. It is believed that fast motility (electromotility) of these cells is essential for this function. Indeed, force produced by outer hair cells follows their membrane potential very closely at least up to 60 kHz. However, it has been pointed out that the cell's receptor potential is attenuated by a low-pass RC circuit inherent to these cells, with the RC roll-off frequencies significantly lower than their operating frequencies. This would render electromotility ineffective in producing force. To address this issue, we assume that multiple degrees of freedom and vibrational modes due to the complex structure of the organ of Corti provide optimal phases for outer hair cells' force to cancel viscous drag. Our derived frequency limit depends on the drag-capacitance product, not directly on the RC time constant. With a reasonable assumption for the viscous drag, the estimated limit is 10–13 kHz, exceeding the RC corner frequency. Our analysis shows that a fast-activating potassium current can substantially extend the frequency limit by counteracting the capacitive current.

INTRODUCTION

The outer hair cell (OHC) is the key element for the sensitivity, dynamic range, and frequency selectivity of the mammalian ear (Liberman and Dodds, 1984; de Boer, 1991; Hubbard and Mountain, 1995). These characteristics of the ear can be realized if the hair cell functions as a feedback amplifier and produces force in such a way that amplifies weak signals.

It was Gold (1948) who first pointed out the need for such an amplifier. He considered that the viscous damping of basilar membrane vibration was quite significant whereas the ear's performance appeared as if it was unaffected by such damping. Based on this observation, he predicted that the ear has a feedback amplifier canceling the effect of viscous drag.

Although it is now thought that the motion of the basilar membrane is not as heavily damped as Gold expected (Rhode, 1971; Patuzzi, 1996), the presence of a feedback amplifier in the cochlea has been widely accepted (de Boer, 1991; Zweig, 1991; Patuzzi, 1996). In recent years it has been hypothesized that the voltage-dependent motility of the outer hair cell's cylindrical cell body, which is referred to as electromotility, make this mechanosensory cell function as the feedback amplifier (Brownell et al., 1985). The amplitude of this motility is ∼5% of the cell length (Ashmore, 1987) and force production by the cell is ∼0.1 nN/mV (Hallworth, 1995; Iwasa and Adachi, 1997). The motile mechanism of the outer hair cell is analogous to piezoelectricity in that it is based on direct electromechanical coupling (Iwasa, 1993; Dallos et al., 1993; Iwasa, 1994; Gale and Ashmore, 1994; Kakehata and Santos-Sacchi, 1995; Iwasa, 2001), in which charge is transferred across the membrane (Ashmore, 1990; Santos-Sacchi, 1991; Iwasa, 1993). Such a motile mechanism can be fast because its speed is not limited by diffusion. Indeed, electromotility produces a phase-locked mechanical force without attenuation at least up to 60 kHz (Frank et al., 1999). Moreover, prestin, a protein that reproduces most of the characteristics of the motor, has been identified (Zheng et al., 2000).

These observations still do not definitively answer the question as to whether voltage-dependent motility is indeed responsible for the cell's functioning as a feedback amplifier. The main reason for this reservation is the so-called “RC time constant” problem. Because the mammalian hearing frequency range extends quite high (to 20 kHz for humans and 40 kHz for guinea pigs), at these higher frequencies the largest part of the mechanotransducer current must be used for charging and discharging the cell's membrane capacitance. It has been argued that the rate of charging and discharging is limited by the resistance of the cell, producing the RC time constant which determines the roll-off of the receptor potential. These roll-off frequencies are significantly lower than the cells' operating frequencies (Housley and Ashmore, 1992). Inasmuch as the cell's force production is voltage-dependent, the attenuation of its receptor potential due to the RC time constant problem will limit its force output.

An additional reservation on the role of electromotility of the OHC is that it may not be the only motile mechanism which can counteract viscous drag. Nonmammalian hair cells, which do not possess somatic motility, produce active force in their hair bundles (Martin and Hudspeth, 1999; Ricci et al., 2000). Because this motile mechanism is directly associated with the hair bundle's mechanotransducer machinery, it does not depend on the cell's receptor potential, and thus experiences no RC time constant problem. Although such force generation has not yet been observed in mammalian hair bundles, these observations provide reason to question the role of electromotility in outer hair cells.

To address the RC time constant problem, here we describe only a local model, a segment of the cochlea that is resonating. Cochlear traveling waves are generated when lateral coupling through fluid is introduced between local segments. The significance of local resonance in the cochlea has been well recognized (Huxley, 1969; Robles et al., 1976), and local resonance can be considered as a limit where the traveling wave's group velocity substantially decreases while within a region of very light damping (Rhode, 1971; Zweig, 1976; Lighthill, 1981).

We will show that OHC electromotility can indeed provide the amplifier function which accounts for the local resonance or light damping region by addressing the following questions:

• Is the outer hair cell's RC time constant really the limiting factor for the effectiveness of its voltage-driven motility?

• What is the frequency limit at which voltage-driven motility of the hair cell can function as an amplifier?

• Can ion channels improve the high-frequency performance of OHC motility? If they do, what would be the characteristics of such channels?

AN “OPTIMIZED PHASE” APPROXIMATION

We start by assuming that voltage-driven motility allows the OHC to function as a feedback amplifier. The effectiveness of outer hair cells in exerting force to modulate the vibration of the basilar membrane is determined by their receptor potential. The receptor potential is in turn determined by the bending of their hair bundles, which depends on the vibration of the cochlear partition. The effectiveness of the force generated will depend on the mode of vibration.

To treat this rather complex system theoretically, various simplifying assumptions have been introduced. Most of those theories simplified the structure of the cochlear partition and limited the degrees of freedom of its motion to capture the dominant modes of vibration (see Patuzzi, 1996, for review).

Instead of simplifying the structure, we simplify our treatment by assuming that this structure is optimally designed to counteract viscous drag. Specifically, we assume that the vibrational modes provide a feedback pathway with the correct phase to optimally exploit the electromotility of outer hair cells. With this approach, we can set an upper limit for the effectiveness of an amplifier that is based on the electromotility of outer hair cells.

We assume that viscous drag due to shear between the tectorial membrane and the reticular lamina constitutes the major part of the drag (Allen, 1980) and that it is counteracted by the electromotility of outer hair cells (see discussion). Viscous drag that acts on the basilar membrane is thought to be less important because the boundary layer is thin at higher auditory frequencies (Freeman and Weiss, 1988; Keller and Neu, 1985).

Assumptions

The major specific assumptions of our approximation are as follows:

1. Bending amplitude of the hair bundles of outer hair cells is proportional to the displacement of the basilar membrane, and is of a similar magnitude.

2. Outer hair cells behave as piezoelectric elements. Their force production is controlled by their membrane potential. Currents elicited by mechanical force applied on these cells are proportional in magnitude with basilar membrane displacements but the phase may differ from that of the basilar membrane.

3. The multiple degrees of freedom in the vibration of the cochlear partition optimizes the phase of OHC feedback force so as to counter viscous drag.

4. The dominant viscous drag in the OHC feedback loop occurs between the tectorial membrane and the reticular lamina (gap drag).

The justifications for and implications of these assumptions are discussed later in a section on cochlear mechanics.

The model

The assumptions that we made are now used to construct a minimal set of equations that describes an outer hair cell feedback loop in vivo.

Let us start with membrane currents. The outer hair cell membrane is exposed to two media, endolymph and perilymph, which differ in their electrolyte compositions as well as in their electric potential (Fig. 1 A). The total membrane current consists of a mechanotransducer current at the apical membrane, which is exposed to potassium-rich endolymph at the endocochlear potential e_ec, potassium currents at the basolateral membrane with the reversal potential e_K, and current due to transferring motor charge (Fig. 1 B). The membrane potential V_m satisfies

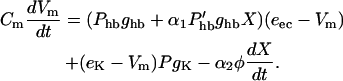(1)

FIGURE 1.

The outer hair cell modeled as a capacitor containing a piezoelectric material which responds with mechanical force to voltage across its cell membrane. (A) Electromechanical feedback loop incorporating the outer hair cell (OHC). The OHC apical surface is a part of the reticular lamina (RL) and has three rows of stereocilia. The tips of the tallest stereocilia maintain firm contact with the tectorial membrane (TM). Its apical surface is bathed in endolymph, high in K⁺ and maintained at the endocochlear potential of ∼+80 mV. The OHC itself is also high in K⁺ with a resting potential of approximately −70 mV. Its basolateral membrane is bathed in perilymph, low in K⁺ and at 0 mV potential. Acoustic stimulation displaces the basilar membrane (BM), which is described by the variable X. Displacement of the BM brings about shear motion between the RL and TM of the same order of magnitude. This shearing stimulates mechanotransduction channels in the stereocilia, producing the receptor potential V_m. OHC force (V_m−V₀)φ counteracts viscous drag −γdX/dt. We ignore direct drag on the basilar membrane itself inasmuch as the major drag originates in the gap between the RL and TM which is mechanically coupled to BM oscillation. This feedback loop consists of an electric part, which is described in more detail in (B), and a mechanical part, which is described in (C). (B) The electrical part of our model based on Eq. 1. Four currents charge and discharge outer hair cell capacitance C_m. Standing current comes in through the transduction channels P_hb g_hb and goes out through the cell's K⁺ conductance P_gK, establishing a voltage operating point near −70 mV. A small voltage oscillation about that point is affected by mechanically oscillating the hair bundle conductance g_hbx. The quantity φ(dX/dt) is the small current necessary to operate the motors and α₁ and α₂ represent phases. (C) The mechanical part of our model based on Eqs. 2 and 3 in which gap drag force −α₁γωx is coupled through an interaction force F_int to the basilar membrane which is modeled as a simple harmonic oscillator. The oscillator consists of local BM mass m coupled to a local spring k. We ignore the smaller direct BM drag. This oscillator is driven by a voltage-dependent motor force (V_m−V₀)φ. Our optimized phase approximation states that the phases α₁ and α₃ provided by cochlear mechanics optimize OHC feedback force so as to counteract viscous resistance dominated by gap drag.

Here, the hair bundle conductance is represented by the product of the maximum hair bundle conductance g_hb and the (resting) open probability P_hb of the transducer channels in the hair bundle. 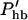is the derivative of this open probability with respect to X, the displacement of the basilar membrane. g_K is the maximum basolateral potassium conductance and P is the open probability of the potassium channel. φ is a piezoelectric coefficient for the outer hair cell motor. Piezoelectric current at the lateral wall is proportional to the rate of length changes of the cell (Dong et al., 2002) and thus is proportional to the velocity of basilar membrane motion. To optimize phase relationships later on, we introduce adjustable phase factors α_n with n = 1, 2, …, which are complex numbers with an absolute value of unity, i.e., |α_n| = 1.

The displacement of the basilar membrane follows the equation,

(2)

because drag on the basilar membrane is not important (see section on cochlear mechanics). Here m is the mass that moves together with a local section of the basilar membrane, ω₀ the natural resonance frequency of the basilar membrane, and F the force applied to the basilar membrane by fluid pressure due to acoustic stimulation (Fig. 1 C).

F_int represents interaction terms with other degrees of freedom or other modes of motion. In a steady state, energy loss due to gap drag is balanced by energy supplied by outer hair cells. Since we assume that the amplitude of basilar membrane motion is the same as the amplitude of gap shear, this energy balance can be translated into force balance if force that is produced by outer hair cells is utilized optimally. This balance leads to the equation,

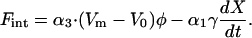(3)

Here (V_m − V₀)φ is the force applied by the outer hair cell due to electromotility. The coefficient φ in the equation is the same as in Eq. 1 because of the piezoelectric reciprocal relationship (Assumption 2) (Dong et al., 2002). The second term is gap drag. As we will discuss later, the boundary-layer thickness is always larger than the gap. Thus, gap drag is proportional to the drag coefficient γ and to velocity, which is in turn proportional to frequency (Batchelor, 1967; Allen, 1980; Nobili and Mammano, 1993).

What results is a one-degree-of-freedom description of basilar membrane vibration in which gap drag directly damps its oscillation (Fig. 1 C), analogous to a one-dimensional rendering (Kanis and de Boer, 1993) of a two-mass system (Neely and Kim, 1986). For example, it can be shown in a two-mass system that condition (Assumption 3) is realized when the ratio of drag force to coupling spring force is small. The argument of α₁ then becomes constrained to near zero by the requirement that gap drag in Eq. 3 functions as a damping factor on basilar membrane vibration.

Gap drag −γdX/dt can be nullified by the effect of hair cell feedback force if their phases oppose whereas the magnitudes of the two terms agree. That is,

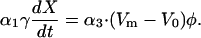(4)

For convenience, we call this “Gold's condition,” which he proposed in his pioneering work (Gold, 1948).

Inasmuch as we are interested in finding the frequency limit of the system, we assume that it is driven by a small acoustic stimulation at frequency ω, and then solve for the steady-state solution. Thus we put,

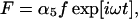(5)

(6)

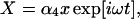(7)

where the quantities expressed by lower case symbols are small.

To proceed we need to know values for the parameters. We show the best estimates for these parameters in Tables 1 and 2. In the following, we examine the first-order terms with respect to these small quantities. Eq. 1 provides a relationship between υ and x,

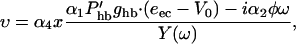(8)

with the membrane admittance

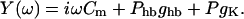(9)

TABLE 1.

Location-insensitive parameters

Parameter	Value
eec	80 mV*
eK	−100 mV†
V0	−70 mV‡
φ	0.1 nN/mV§

^*Békésy (1952); Basal turn more positive than apical turn by ∼20 mV (Salt et al., 1989).

^†The Nernst potential with 140 mM K⁺ inside and 2.7 mM K⁺ outside the cell.

^‡Cody and Russell (1987).

^§Iwasa and Adachi (1997).

TABLE 2.

Location-sensitive parameters

	Apical	Basal
Cm	45 pF*	15 pF*
gK	2 nS†	50 nS* 100 nS§
ghb	0.8 nS‡	28 nS¶
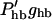	0.03 nS/nm	1 nS/nm‖
γ	0.3 × 10−7 Ns/m	1.4 × 10−7 Ns/m**

^*Housley and Ashmore (1992)

^†Mammano and Ashmore (1996)

^‡Assumes that the equilibrium current through g_K driven by V₀ − e_K ≈ 30 mV equals the current through half open g_hb, driven by e_ec − V₀ ≈ 150 mV.

^§Russell et al. (1986a)

^¶The largest observed 9.2 nS hair bundle conductance in perilymph (Kros et al., 1992) multiplied by 3 to account for increased conductance in low Ca⁺² endolymph (Kros, 1996).

^‖Obtained by multiplying the steepest slope for hair bundle open probability (25 nm)⁻¹ (Russell et al., 1986b) by the highest estimate for hair bundle conductance g_hb ≈ 28 nS (Kros, 1996; Kros et al., 1992). We have assumed a 1:1 ratio between hair bundle displacement and basilar membrane displacement (see cochlear mechanics discussion).

^**Per outer hair cell values for the viscous drag of the gap between the tectorial membrane and reticular lamina (see text after Eq. 11).

Numerical examination shows that the second term iα₂φω in the numerator of Eq. 8 can be ignored because it is much smaller than the first term (see Piezoelectric Resonance discussion). Next, we substitute for υ from Eq. 8 into Gold's condition (Eq. 4) so that it reads

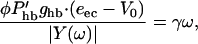(10)

where the phase parameters have been adjusted so that OHC force opposes the drag.

CAPACITANCE AND DRAG SET THE LIMITING FREQUENCY

Eq. 10 shows that we need to know the admittance Y(ω) of the cell membrane to determine the frequency that satisfies Gold's condition. The admittance Y(ω) consists of a capacitive part, which is proportional to the frequency, and a conductive part.

Let us examine the relative importance of the capacitive current in apical and basal hair cells. If the apical hair cell characterized in Tables 1 and 2 would operate at 100 Hz then its capacitive admittance is 28 nS, about an order-of-magnitude larger than its ionic conductance. A basal cell that operates at 10 kHz has a capacitive admittance of ∼1 μS, also about an order-of-magnitude larger than the cell's ionic conductance, which is much larger than that of apical cells. Thus, both apical and basal cells are dominated by capacitive admittance (|Y(ω)| ≈ ωC_m).

Gold's condition Eq. 10 becomes

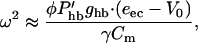(11)

which gives the frequency limit, above which the efficiency of the outer hair cell as a cochlear amplifier sharply declines. This limiting frequency does depend on the capacitance as expected but not directly on the RC.

To obtain the frequency limit, viscous drag needs to be evaluated. Periodic motion in a fluid is characterized by a viscous boundary layer, which is defined by (Batchelor, 1967)

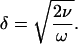(12)

Here ν is the kinematic viscosity of the fluid, which is the viscosity η divided by the density ρ. For length scales smaller than δ, corresponding to a Reynolds number less than one, drag force predominates over inertial force (Freeman and Weiss, 1988).

The thickness of the boundary layer δ is ∼48 μm at 100 Hz and 5 μm at 10 kHz with the value 0.72 × 10⁻³ Pa · s for the viscosity of perilymphatic fluid (Dahl and Kleinfeldt, 1976). The gap between the tectorial membrane and the reticular lamina should be about the same as the length of the stereocilia, which is ∼5 μm at the cochlear apex (100 Hz) and 1 μm near the base (10 kHz) (Lim, 1980). The gap appears to be always shorter than the boundary layer (Freeman and Weiss, 1988). Thus we can evaluate its drag by the formula ηSU/d, where S is the area of one of the confining plates, d is the gap, and U is the relative velocity of the two plates (Batchelor, 1967).

For apical cells, the the gap is ∼5 μm. One of the two confining plates is 60 μm long by 10 μm wide for a single row of three outer hair cells and one inner hair cell. Shear drag within this gap is shared by three outer hair cells so that the drag per OHC is equivalent to the Stokes drag on a sphere 4 μm in diameter. The resulting frequency limit is ∼3 kHz, much higher than cell's operating frequency of 100 Hz, which is yet higher than its RC corner frequency of ∼10 Hz. This means that apical hair cells are capable of generating more active force than Gold's condition requires. In addition, the RC corner frequency does not directly limit their performance.

For basal hair cells, however, capacitive current and gap drag do impose an upper limit. Although the area per outer hair cell is about the same as apical turns, the gap d is ∼1 μm for the basal turn. Thus viscous drag is equivalent to a Stokes sphere 21 μm in diameter. Then our set of parameter values for basal hair cells, which could be regarded as somewhat favorable, leads to a limiting frequency of 13 kHz. Although this frequency is much higher than the RC corner frequency of 1 kHz, it is also much lower than 40 kHz, the upper limit of the auditory range for guinea pigs.

The so-called RC time constant problem is not relevant when outer hair cells are integrated into the cochlea where slope hair bundle conductance dominates the charging of the cell. Whereas the cell's capacitance C_m is an important factor, the membrane resistance (or conductance) enters only indirectly. Instead, the factors important for the characteristic frequency are the sensitivity of hair bundle current to basilar membrane displacement, a piezoelectric parameter of the motor, and the viscous drag. Our analysis thus predicts that electromotility is sufficiently effective except for the basal turn, where the characteristic frequency is between 7 and 40 kHz. To operate at the high frequency end of the basal turn, outer hair cells appear to require a mechanism in addition to electromotility.

EFFECT OF LARGE NONLINEAR CURRENTS

Are there any ways of reducing the capacitive current, which increases with frequency, to control the magnitude of the admittance Y(ω)?

If ion currents are linear (Ohmic), the ionic conductance increases the absolute value |Y(ω)| of the admittance function because the phases of the capacitive and conductive components are perpendicular in the complex plane and no destructive interference is possible.

However, if ion currents have voltage-dependent kinetics, leading to delayed openings, then the phases of the ionic and capacitive currents can be opposed and, consequently, destructive interference can take place. Such destructive interference can reduce the admittance, raising the frequency limit. In the following, a couple of simple limiting examples are examined.

Two-state channel

Let us consider that a short OHC contains a voltage-dependent potassium channel that has one open state and one closed state. Gating of this channel is represented schematically,

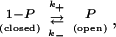where k₊ and k₋ are transition rates. The probability that this channel is open at time t after the membrane potential is clamped to V_m follows a Hodgkin-Huxley type differential equation,

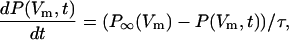(13)

where the relaxation time of the channel is given by τ = 1/(k₊ + k₋). P_∞(V_m) is the equilibrium open probability at membrane potential V_m.

Corresponding to an oscillating membrane potential V_m (=V₀ + υ exp[iωt]), the open probability P of the channel is divided into a steady-state component and an oscillating component,

(14)

By substituting Eqs. 14 and 6 into Eq. 13, we obtain

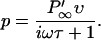(15)

This term contains both a real part, which is in phase with the voltage, and an imaginary part, which lags behind the voltage. is the voltage derivative of P_∞(V₀).

By substituting Eq. 15 into Eq. 9, we find that the square of the absolute value of the admittance is

(16)

where g_g is the slope conductance of the potassium channel due only to its gating,

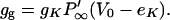(17)

Eq. 16 shows that the nonlinear current reduces the effective capacitive current, but also increases conductive current. Because the channel time constant can be chosen so that its effect on capacitive current is greater (ωτ > 1), the net result is a decrease of the magnitude of the admittance. With this mechanism, the magnitude of the admittance can be reduced by a factor of two and extend the frequency limit up to twofold (Fig. 2 C).

FIGURE 2.

Comparison of two-state and multi-state voltage-gated K⁺ channels in their ability to reduce OHC admittance and raise operating frequency. (A) Free energy profile of a two-state channel (2SC) and that of a hypothetical four-state channel (4SC). A positive jump in the membrane potential elicits an increase in the open probability of the 2SC with an exponential time course. For the illustrated 4SC, the immediate response is a transition from O3 to C2 on depolarization. This is followed by an increase of the O4 population at the expense of the C1 population. Thus, an initial closing response is followed by an opening upon depolarization, creating a delayed outward current. (B) Four currents elicited by a square voltage pulse: RES, resistive current; 2SC, a simple two-state, voltage-gated K⁺ channel; 4SC, a four-state, voltage-gated K⁺ channel; and IND, a perfect inductor in series with a small resistor. The 2SC has a resistive current component due to the channel being partly open at rest. The 4SC first passes current inwardly, effectively reducing the cell's real conductance, before its current turns outward. Thus it mimics an inductive current much better than a 2SC. (C) Performance of a 2SC current in reducing OHC admittance. Contour plot of the admittance Y against conductance g_g and the channel's gating rate constant 1/τ · g_g is the slope conductance of the K⁺ channel due only to its gating. The Ohmic conductance of the cell at its operating point includes the dominant basolateral K⁺ conductance along with hair bundle conductance. ω is the angular frequency. The frequency limit at which the OHC is able to counteract drag is inversely proportional to its admittance. (D) example showing the performance of a 4SC current in reducing OHC admittance. Along the 0.1 contour, virtually all capacitive admittance is eliminated. The 4SC contains an additional fast off current (negative conductance) which eliminates the conductance terms while leaving the slower “inductance” term in Eq. 16 virtually undisturbed.

From Eq. 16, we can obtain a two-state channel's equivalent inductance under a special condition. If ωτ is large, the imaginary part of a two-state channel's admittance is g_g/(ωτ). Comparison with the 1/(ωL) of an inductor provides that L = τ/g_g. The corresponding resonance frequency is 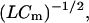implying that L must be small to operate at high frequencies. This means that g_g must be large and τ must be small. How does this inductance compare with known values of other cells? The squid giant axon, with slow potassium channels at a relatively low density, has a specific inductance of 0.2 H cm² (Cole, 1968). Applying the specific inductance of the squid to a short OHC with a surface area of ∼800 μm², we obtain ∼2.5 × 10⁴ H. Given the cell's capacitance this is several-orders-of-magnitude too large to support resonance above 10 kHz. To estimate the inductance of OHC, substitute into L = τ/g_g channel parameters which are appropriate to a short base coil OHC: (V₀ − e_K) = 30 mV, g_K = 100 nS, 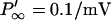for a voltage sensitivity s = 3 mV, and τ = 50 μs. This leads to an inductance of 130 H.

Although a two-state channel is not very effective in elevating the operating frequency, the channel does not have to be particularly fast compared to this operating frequency and its time constant does not have to be narrowly tuned.

Channels with more complex gating

In the following, we examine gating kinetics that are more favorable for sustaining a very high frequency electrical oscillation. One prominent difference between inductive current and current due to a two-state channel is in their instantaneous response to a voltage pulse. Whereas two-state channel current has a component that instantaneously increases on a voltage jump, inductive current does not (Fig. 2 B). This feature can be mimicked by ion channels with multiple states.

Let us consider a four-state potassium channel with two closed states, c1 and c2, and two open states, o3 and o4 (Fig. 2 A). Suppose the energy levels c1 and o3 go up and c2 and o4 go down on depolarization. Then, on depolarization, the open probability of the channel can quickly decrease before its increasing with a delay (Fig. 2 B). A current through this four-state channel considerably improves the high-frequency performance of short outer hair cells (Fig. 2 D).

The more effective reduction of admittance by a four-state channel can be understood as reduction of the conductance term P_∞(V₀)g_κ by initial early negative conductance due to a fast gating process. The minimum of the admittance ratio is very low. In an example shown in Fig. 2 D, it is lower than 0.001. Because the limiting frequency ω and the admittance are related by Eq. 10, this means that the frequency limit can exceed 100 kHz, high enough to make outer hair cells effective as an amplifier in the auditory range of all mammals even including bats provided that the motor is fast enough to be able to phase-lock to the membrane potential.

A mechanism similar to this multiple-state channel is known in hair cells of the turtle and the frog (Crawford and Fettiplace, 1981; Hudspeth and Lewis, 1988). In these cells, a combination of two currents produce a phase delay. Voltage-gated calcium channels are colocalized with calcium-gated, large conductance potassium channels (Roberts et al., 1990). Upon depolarization, an inward current due to Ca²⁺ is activated at first, but as Ca²⁺ accumulates inside the cell the Ca²⁺-gated potassium channel is activated, eliciting an outward current. Eventually potassium current dominates, reversing the direction of the total current. This mechanism would be advantageous for hair cells of the frog and the turtle because these cells operate at relatively low frequencies (≈100 Hz). We speculate that this mechanism may not be suitable above 10 kHz because it is dependent on Ca²⁺ binding/unbinding kinetics, diffusion, and buffering.

TRANSFER FUNCTION NEAR RESONATING POINT

To determine the frequency limit, we have analyzed our basic Eqs. 1 and 2 by linear expansion. Then we imposed Gold's condition (Eq. 4) that viscous drag is counteracted by force produced by hair cells. For this purpose, we used the maximum value for displacement-to-conductance sensitivity of the hair bundle.

The dominant nonlinearity of the system is the displacement-to-conductance transfer function of the hair bundle. In our linearized treatment, it was expanded to the first-order term (Eq. 11), giving rise to 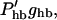where 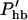was considered constant. We now assume that the transfer function P_hb is not a constant but a Boltzmann function of basilar membrane displacement X and return to Eqs. 1 and 2. We first solve these equations numerically. Then we analytically show that our system is poised on a Hopf bifurcation when Gold's condition is met.

When Gold's condition is satisfied, i.e., the drag is exactly canceled by the membrane motor force, the basilar membrane's force-to-displacement transfer function take the shape of a cube-root (Fig. 3, A and B). As we show below, such behavior is a generic property of a Hopf bifurcation, a dynamical instability which occurs when a feedback oscillator has sufficient positive feedback so that it begins to “ring” spontaneously at small amplitude (Eguíluz et al., 2000).

FIGURE 3.

Simulation of our model's performance at high frequency (9.2 kHz) when it includes a two-state, large, fast, voltage-dependent K⁺ conductance, placing the system very near to a Hopf bifurcation. By reducing the voltage-dependence of this conductance, the same system shows low-gain, linear performance. (A) BM amplitude plotted against external forcing. The system shows a compressive nonlinearity in its transfer function when it is poised on a Hopf bifurcation, and linear behavior when poised well below the bifurcation by turning off the voltage sensitivity of the K⁺ current. (B) Log–log re-plot of (A). The slope near the zero-crossing is ⅓, the dependence expected for a system poised on a Hopf bifurcation. Because the simulation cannot be poised exactly at the bifurcation, there is a small-amplitude forcing region with a linear transfer function. When the voltage-dependence of the fast K⁺ conductance is absent, the model meets Gold's condition, or poises on a Hopf bifurcation, at 6.2 kHz. Increasing the voltage-sensitivity of the fast K⁺ conductance raised the frequency limit to 9.2 kHz (The channel's gating time constant is 30 μs. Its voltage sensitivity s of e-fold current increase was changed from 100 to 2 mV).

In the following we show the cube-root dependence of the basilar membrane's transfer function. First consider a simple harmonic oscillator, which is described by

(18)

Here the oscillator with mass m is subjected to drag, which is characterized by a drag coefficient γ, and driven by periodic external force F having frequency ω. If the frequency of driving force is the same as the resonance frequency ω₀ of the oscillator, F = iγω₀x. Thus, the phase of the external force F must match that of the velocity iω₀x.

We apply a similar argument to match phases in our model and obtain,

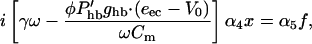(19)

from Eqs. 1, 2, 5, and 7. Now with Gold's condition, the left side vanishes if is treated as a constant. However, whereas P_hb is in fact a Boltzmann function (Russell et al., 1986b), its higher order terms will become important,

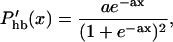(20)

where a is a constant. If this is expanded near its peak (x = 0), we obtain

(21)

Because Gold's condition drops the first (constant) term together with the drag, the second term in Eq. 21 dominates the left side of Eq. 19. Thus x³ is proportional to external forcing f and we obtain the cube-root dependence of the transfer function expected for a system poised on a Hopf bifurcation.

Our analysis demonstrates that on resonance our model, with or without fast potassium conductance, has a cube-root shaped force-to-basilar membrane displacement transfer function (Ruggero, 1992). This result is due to the saturating nonlinearity in the feedback loop, which is described by a Boltzmann function. Without fast potassium conductance the main source of nonlinearity is in the hair bundle's mechanical sensitivity.

DISCUSSION

Fast-activating currents

Our theory predicts that voltage-dependent, large, fast currents should be present in outer hair cells that operate at frequencies above ∼13 kHz. These currents are unnecessary in hair cells that operate at lower frequencies. According to the frequency-location map (Greenwood, 1990), above 7 kHz corresponds to the base turn of the guinea pig cochlea. Further we predict that the effectiveness of these currents will critically depend on their detailed time courses of activation.

In the literature, there are two kinds of reports on ionic currents in basal outer hair cells. One of them uses whole-cell voltage clamp on isolated outer hair cells. Current records were obtained from an outer hair cell, isolated from the basal turn with enzyme digestion (Housley and Ashmore, 1992). The length of the cell is 22 μm. Its conductance is ∼50 nS and weakly nonlinear. The other is an in situ current clamp experiment (Russell et al., 1986a). The resting conductance is ∼100 nS and has a very strong outward rectification (e-fold conductance increase for s = 3 mV), which would be consistent with our prediction. These two kinds of reports have been recognized as inconsistent (Kros, 1996). More recently, fast potassium currents have been found in isolated inner hair cells (Kros et al., 1998) making the absence of fast channels in isolated outer hair cells all the more counterintuitive and puzzling. As Kros has emphasized in his review, cell properties could be significantly altered by the isolation process, so that it is likely that the in situ data (Russell et al., 1986a) better reflects the in vivo condition.

To resolve this problem, we are currently examining outer hair cells for fast activating currents. Our preliminary results indicate that short outer hair cells from the basal turn do in fact have fast-activating, outwardly-rectifying currents. The conductance we have observed is large (>100 nS) and it activates in much less than 1 ms at 22°C (Ospeck et al., 2002). These fast-activating currents are absent in outer hair cells from more apical turns. Although those apical outer hair cells do have outwardly-rectifying currents, their activation times are greater than 10 ms (Mammano and Ashmore, 1996), much too slow to counteract capacitive current.

Cochlear mechanics

The local resonance model that we propose is based on four assumptions. Here, we briefly discuss issues in cochlear mechanics related to these assumptions.

The significance of local resonance

It has been shown that local resonance is an essential element of the mechanics of the cochlea (Huxley, 1969; Patuzzi, 1996). However, unlike a harmonic oscillator's classical resonance peak, the ear's resonant spectral shape is not symmetric with respect to a specific location's characteristic frequency but shows a steep high-frequency cutoff instead. The reason for the asymmetry is due to wave propagation which starts at the cochlea's high-frequency end. Cochlear traveling waves slow down considerably although growing in amplitude as they approach their respective resonance points and then diminish rapidly as they pass the resonance point (Zweig, 1976; Lighthill, 1981). Wave energy is absorbed at the resonance so that the cochlea behaves like a wave-guide with a high frequency cutoff.

Shear flow in the gap and basilar membrane displacement

The shearing motion of the fluid between the tectorial membrane and the reticular lamina is indispensable to the ear because the stereocilia of the inner hair cell is driven by this shear flow (Freeman and Weiss, 1988). We have already discussed how to evaluate the drag due to shear motion within the gap, assuming a 1:1 ratio of basilar membrane displacement to the shear (Table 2; Assumption 1). In the following we discuss the basis for this ratio.

In a system with multiple degrees of freedom, the amplitude of one mode of motion does not necessarily determine the amplitude of another mode. However, the amplitude of basilar membrane displacement and neural output have a tight correlation (Ruggero, 1992). Also the relative movement of the plates that form the gap is the same as the deflection of the OHC hair bundle. We estimate a 1:1 ratio of hair bundle displacement to displacement of the basilar membrane based on the following comparison: The bundle is gated from full closed to full open by a deflection of only 80 nm (Russell et al., 1986a). The transfer function for the basilar membrane undergoes a transition from a compressively nonlinear regime to a linear one for ∼100 nm peak-to-peak oscillations (Johnstone et al., 1986; Ruggero, 1992). Loss of compressive nonlinearity indicates that the amplifier is being turned off, which should approximately coincide with the hair bundle oscillating between its full closed and full open states—hence the ratio of hair bundle deflection to basilar membrane displacement should be ∼1:1.

Significance of gap drag

We assumed that gap drag is the dominant component of the drag in the cochlea and has significant effects on its vibration (Assumption 4). We will briefly discuss the validity of this assumption.

It has been experimentally observed that the Q factor in the base coil is sensitive to the ear's condition—Q is greatly diminished when the ear dies (see Patuzzi and Robertson, 1988, for review). Sensitivity also decreases reversibly near the characteristic frequency when the endocochlear potential is eliminated by furosemide (Ruggero and Rich, 1991). This reduction in the sensitivity is accompanied by phase lag of ∼77°. These experimental observations can be understood that drag is indeed important in the basal turn of the cochlea. To reduce gap drag by an active mechanism, more force is required in the basal turn than in the more apical turns because Eq. 2 indicates increased drag force at higher frequencies.

In addition to the gap itself, the stereocilia of inner and outer hair cells can contribute to drag. Of the two, we can ignore drag on the stereocilia of outer hair cells. Because the tips of stereocilia of outer hair cells are embedded in the tectorial membrane, these stereocilia are bent at their roots by shear motion of the gap d. The velocity field of the fluid is linear because the gap is smaller than the thickness of the boundary layer δ. Thus, the relative motion between the fluid and the stereocilia of outer hair cells is too small to result in significant drag. The hair bundles of inner hair cells may be a more important factor. Because they are freestanding, they bend depending on the balance between drag and bending stiffness. The upper bound of hair bundle drag can be evaluated by using an equivalent cylinder of 10 μm diameter in a shear field (Freeman and Weiss, 1988). Our estimates show that hair bundle drag of an inner hair cell is ∼10% of gap drag for apical cells and only ∼0.5% for basal cells.

Drag that works on the basilar membrane has been modeled. The model indicates that basilar membrane drag is too small to affect cochlear mechanics significantly (Keller and Neu, 1985).

Another important source of drag is the interior of the organ of Corti. This drag is very difficult to evaluate because detailed information on the mode of deformation of the organ is required. We can provide only a crude estimate. Assume that a quarter wavelength near the resonance point is of the cellular dimension of ∼10 μm (Zweig, 1976) (according to a recent experimental report (Ren, 2002), the wavelength is ∼150 μm) and that basilar membrane vibration accompanies changes in thickness of the organ of Corti. Because organ of Corti is filled with fluid, changes in its thickness elicit fluid flow, resulting in drag due to exposed cells. For the sake of order estimation, we further assume that the amplitude of thickness change is the same as the amplitude of basilar membrane vibration and that the depth of the fluid space in the organ is the same as the length of the outer hair cell. The resulting drag per outer hair cell is dependent on the wavelength, the fluid viscosity, and the velocity of basilar membrane. The ratio of internal drag evaluated in this way to gap drag per outer hair cell is 3d/δ, which is ∼0.6 for the basal turn. Thus, this term can reduce the limiting frequency from 13 kHz to 10 kHz. In more apical turns, this correction is less significant.

Our crude estimate appears reasonable from an evolutionary view point. The highly organized organ of Corti is a mammalian innovation that is associated with extending the hearing range into higher frequencies. Thus the structure of the organ of Corti likely minimizes its internal drag so as not to overwhelm gap drag, which is indispensable for the ear to function.

Piezoelectric resonance

The motile mechanism of outer hair cells is based on highly effective and nonlinear piezoelectricity. In this sense, the mechanism that we propose can be called piezoelectric resonance (Mountain and Hubbard, 1994). However, it is not “pure” piezoelectric resonance that is based upon an inductance in the equivalent circuits of piezoelectric elements (Ikeda, 1990). A combination of capacitance and inductance forms a resonating circuit, which can overcome the low pass RC filter in sustaining electric oscillation at frequencies higher than the RC roll-off frequency. However, our high-frequency analysis requires that hair cells function simply as an efficient motor and ionic currents function as the inductive element. Why doesn't the system behave as a much simpler piezoelectric resonator?

In our treatment presented above, we ignored the piezoelectric reciprocal effect term in Eq. 8 because for basal OHC parameter values at 10 kHz it is more than an order-of-magnitude smaller than the hair bundle conductance term. If instead we ignore the hair bundle term in favor of this reciprocal effect φω due to the motor, we obtain

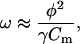(22)

instead of Eq. 11. Eq. 22 obviously represents the piezoelectric resonance frequency, which is only ∼750 Hz for our basal OHC parameter values. Should the piezoelectric coefficient φ be made larger by a factor of four without significantly increasing cell capacitance, then the reciprocal effect of the motor would be important at 10 kHz. However, in order for piezoelectric resonance to prove useful for the ear of bats, which typically have thresholds below 0 dB SPL at 80 kHz (Kössl and Vater, 1995), a prohibitively large piezoelectric coefficient φ would be required.

CONCLUSIONS

We propose an “optimized phase” approximation to characterize the outer hair cell feedback loops near to a local resonance inside the mammalian cochlea. This approximation provides the optimal condition for those hair cell's somatic electromotility to counteract viscous drag so as to establish a low loss, or high Q resonance. When we include the transduction channel's saturating nonlinearity in our model we can reproduce the compressive nonlinearity of the mammalian ear's transfer function. Such a nonlinearity is due to the outer hair cell feedback loop being poised on a Hopf bifurcation.

Our estimate of the upper frequency limit at which electromotility is effective for the mammalian ear is between 10 and 13 kHz. Outer hair cells, except those in the basal turn, should not need any additional mechanism that enhances the effect of electromotility. Those in the basal turn can have their frequency limit raised severalfold if electromotility is aided by fast, voltage-gated ion channels, which mimic inductance. We predict that such “inductive” channels are present in outer hair cells of the basal turn of the cochlea.