Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2003 Feb;84(2):750–756. doi: 10.1016/S0006-3495(03)74894-2

Prediction of Secondary Ionization of the Phosphate Group in Phosphotyrosine Peptides

M Wojciechowski *, T Grycuk *, J M Antosiewicz *, B Lesyng *,†
PMCID: PMC1302655  PMID: 12547759

Abstract

A computational approach, based on a continuum molecular electrostatics model, for the calculation of the pKa values of secondary ionization of the phosphate group in phenyl phosphate derivatives is described. The method uses the ESP atomic charges of the mono-anionic and di-anionic forms of the ionizable phosphate group, computed with the use of the density functional method, and applies a new concept of the model group, being the reference state for the pKa calculations. Both conformational flexibility and tautomeric degrees of freedom are taken into account in the calculations. The method was parameterized using experimentally available pKa values of four derivatives of phenyl phosphates, and phosphotyrosine. Subsequently this parameterization was used to predict pKa of the phosphate group in a short peptide Gly-Gly-Tyr(P)-Ala, and in a longer peptide consisting of 12 residues, the latter in water, and in a complex with a protein—phospholipase. The agreement between the computed and the experimental pKa values is better than ±0.3 pH units for the optimized solute dielectric constant of 11–13. This approach is promising and its extension to other phospho-amino acids is in progress.

INTRODUCTION

Phosphate groups play a key role in the living world. They are present in proteins, nucleic acids, and other biomolecular systems, and no other residue appears to fulfill the multiple roles in molecular biology (Westheimer, 1987). Reversible phosphorylation of seryl, threonyl, tyrosyl, or histydyl residues is one of the most abundant covalent modifications of proteins which constitutes an ubiquitous mechanism for controlling and regulating intracellular processes (Greengard, 1978; Walaas and Greengard, 1991; Beltman et al., 1993; Kurosawa, 1994; Dekel, 1996; Patarca, 1996). A phosphate group bound to an amino acid side chain has either a single- or double-negative charge. The primary pKa values of phosphoric acid and of phosphate mono-esters are ∼2, which results in their at-least mono-anionic ionization state at physiological pH. The secondary pKa of phosphoric acid is 7.2 according to one source (Weast, 1966) and 6.7 according to the other (Peacock and Nickless, 1969). Also, the secondary ionization constant of the phosphate group in well-solvated phosphate mono-esters is close to the value of 7. What is important, the total charge of the phosphate groups in phospho-amino acids in a complex molecular environment can be either −1 or −2. A knowledge of whether the phosphate group is di-anionic or mono-anionic, in particular, if the ionization state is affected by the presence of ligands or other changes in the environment, is essential for understanding the role played by this group in catalytic events or in protein structure formation (Martinez-Liarte et al., 1992; Johnson and Barford, 1994; Yang et al., 1994; Mavri and Vogel, 1996; Mestas and Lumb, 1999; Antosiewicz et al., 2000). Ionization state of the bound phosphate group in a protein or polypeptide can be determined by NMR spectroscopy methods (Kalbitzer and Rösch, 1981; Hoffmann et al., 1994) or a Fourier transform infrared spectroscopy (Sanchez-Ruiz and Martinez-Carrion, 1986). On the other hand, during the past several years a significant progress in the development of increasingly predictive theoretical models for protonation equilibria in proteins is observed (Bashford and Karplus, 1990; Yang et al., 1993; Antosiewicz et al., 1994, 1996; Sham et al., 1997; Mehler and Guarnieri, 1999). The previous theoretical approaches dealt rather exclusively with standard amino acids encountered in proteins. Inasmuch as phosphorylation is common in proteins, it would be desirable to also include phosphorylated side chains in the list of residues treated in standard modeling methods. In this study an approach for prediction of the secondary ionization constant of phosphotyrosine (pTyr) in polypeptides and proteins is proposed.

METHODS

Theoretical background

A number of methods for theoretical prediction of protonation equilibria in proteins use a concept of the model compound, which usually meant an isolated amino acid, and an assumption that the difference in protonation behavior of the model compound in an isolated state in solution, for which the ionization constant is assumed to be known, and the protonation behavior in the protein environment, is purely electrostatic in origin (Bashford and Karplus, 1990; Yang et al., 1993; Antosiewicz et al., 1994, 1996; Sham et al., 1997; Mehler and Guarnieri, 1999). Typically, the corresponding electrostatic energies are calculated for the model compound with frozen conformations as they appear in the protein structural file. A possibility of conformational movement of the protein was included in a different manner by some authors (You and Bashford, 1995; Zhou and Vijayakumar, 1997).

The present method makes one step further toward improvements of the prediction of proton equilibria in proteins. Namely, instead of the model compound, a model group is introduced with its pKa(model) which can be determined based on experimental pKa values of small molecules containing the given group. The model group is characterized by the lowest possible conformational flexibility, and it is reduced only to those atoms which change their charge during deprotonation. A new understanding of pKa(model) was presented in full detail elsewhere (Grycuk, 2002); therefore, only the main features of this approach are presented below.

The standard free enthalpy of proton dissociation can be expressed as follows:

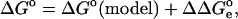graphic file with name M1.gif (1)

where the 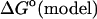Inline graphic term refers to the model system, and 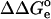Inline graphic represents the electrostatic correction to the standard free enthalpy 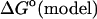Inline graphic. The pKa of the proton dissociation reaction is given as:

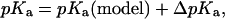graphic file with name M5.gif (2)

where the contribution Inline graphic arises from the averaged interaction between the model system and the rest of the molecule, and the Inline graphic refers to the model system. For a molecule with fixed conformation the following is valid:

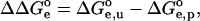graphic file with name M8.gif (3)

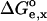where Inline graphic (x = p or u for the protonated and deprotonated state, subsequently) represents the electrostatic work of moving the model group from solvent to the molecule. A meaningful relation between pKa and pKa(model) can be obtained if 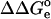Inline graphic is computed taking into account the representative ensemble of conformations of the molecule. The free enthalpy change, 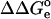Inline graphic, is defined as in Eq. 3, but now the contributions 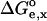Inline graphic represent the averaged electrostatic corrections for both protonation forms, and they are calculated as follows:

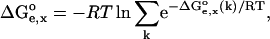graphic file with name M13.gif (4)

therefore, finally:

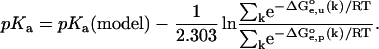graphic file with name M14.gif (5)

The summation extends over a representative ensemble of conformers sampled from the trajectory of the Molecular Dynamics simulation with suppressed electrostatics. The form of Eq. 5 indicates that contribution of each conformer to the relation between pKa and pKa(model) is weighted by the electrostatic work of moving the model group from solvent to the molecule, 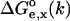Inline graphicfor the k-th conformer. This equation allows one to estimate the pKa(model) based on the experimental pKa of a small molecule containing the model group.

The calculated value of Inline graphic depends on atomic partial charges and radii of the solute molecule, as well as on the solute and solvent dielectric constants and definition of the dielectric boundary between solute and solvent. For each set of these parameters and definition of the boundary, the pKa(model) reproducing the experimental pKa values of a given molecule can be determined. In practice partial charges and radii of atoms are established independently. This leaves a solute dielectric constant and the pKa(model) as the only adjustable parameters in the model being applied for prediction protonation equilibria based on the Poisson-Boltzmann model of solute-solvent systems.

Having experimental pKa values of a number of small test molecules containing the same model group, one can choose the solute dielectric constant and corresponding pKa(model) according to Eq. 5 which give the best reproduction of the experimental data for all the test molecules. Such a procedure leads to solute dielectric constant substantially above values expected on the basis of only electronic polarization contribution. It should be stressed that the resulting pKa(model) and the solute dielectric constant are not direct, physical observables and their values are adjustable parameters.

Atomic partial charges and force field parameters

Calculation of the electrostatic energy requires atomic charges and radii. The atomic radii were taken from the CHARMM force field. Charge parameterization for phosphotyrosine in two protonation states of the phosphate group is available (Feng et al., 1996), but the corresponding partial charges data for phenyl phosphate derivatives is not. Therefore, in this study a set of atomic charges that fit the electrostatic potential in the gas phase, so-called ESP charges, were computed using the Gaussian94 package (Frisch et al., 1995). The density functional method, with the B3LYP exchange and correlation functional and the 6–312+g(d,p) basis set, was chosen.

The ESP charges were computed for all phenyl phosphate derivatives and for phosphotyrosine, for both ionization states of the phosphate group, i.e., the single- and double-ionized states. The calculations were carried out for a set of molecular conformations of each molecule covering the available conformational space of the system. The resulting charges were averaged over all conformations. Some charges were additionally averaged due to the local symmetry, e.g., CD1 and CD2 carbon atoms of the benzene ring. Such approximation removes problems of predefined asymmetry.

One should note that the ESP charges were used exclusively in the Poisson-Boltzmann calculations. The Molecular Dynamics simulations were carried out with electrostatics switched off (see the next paragraph), and the remaining parameters for these molecules were taken from the CHARMM force field. Based on the computed ESP charges, the model group for phenyl phosphate and its parameterization was proposed (see ESP charges in Results).

Generation of an ensemble of structures

For all molecules considered in this study but the phospholipase-dodecapeptide complex, an ensemble of structures was generated by Langevin Dynamics method (Widmalm and Pastor, 1992) using the CHARMM v2.26 software (Brunger and Karplus, 1988). The electrostatic interactions were switched off, therefore the sampled structures were not weighted by electrostatic energies. The simulation procedure consists of a short minimization, a 6-ps equilibration, and the 200-ns dynamics. The Langevin Dynamics was carried out with a 2-fs time step and the friction coefficient FBETA = 50 ps−1. To avoid translational movement of the whole system, a harmonic constraint was applied to the central atom. After each 100 ps of dynamics, the current structure was saved, leading finally to an ensemble of 2000 conformers. Adding new conformers did not change the value of the pKa(model). In the case of phospholipase-dodecapeptide complex, a set of 18 NMR-based structures was used (Pascal et al., 1994), available in the Protein Data Bank (PDB; Bernstein et al., 1977) under access code 2PLE.

Parameterization of the pKa(model) versus solute dielectric constant

For each structure sampled from the Langevin trajectory, the electrostatic contribution to the free enthalpy was calculated using the UHBD software (Davis et al., 1991). The method is based on a continuum dielectric model, and the linear form of the Poisson-Boltzmann equation. The equation was solved using a finite difference method (FDPB). We used standard parameters for the solvent dielectric constant (78.0 for water), solvent probe radius of 1.4 Å, ion strength of 150.0 mM, and ion exclusion radius of 2.0 Å. There is no standard value of the solute dielectric constant for proteins; its value changes depending on the local environment, the approximations made, and the atom charges applied (Gilson and Honig, 1986; Nakamura et al., 1988; Sham et al., 1997; Schutz and Warshel, 2001). To find the most appropriate solute dielectric constant for the phosphate group in phenyl phosphates and related compounds, the four phenyl phosphate derivatives and phosphotyrosine were parameterized as follows. The 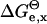Inline graphiccontributions (see Eq. 4) for all these molecules, for the protonated and deprotonated states of their titratable sites, were computed for the solute dielectric constant ranging from 5 to 20. These energies allow parameterization of the pKa(model) as a function of the solute dielectric constant, using Eq. 5.

Experimental data for all the molecules are presented in Table 1. The experimental data for the first five molecules were used for parameterization, and the data for the last three molecules were used for comparison between the experiment and our theoretical prediction.

TABLE 1.

Experimental pKa values for the examined molecules

Molecular system pKa Ref.*
Phosphoric acid monophenyl ester 5.83 [1–5]
Phosphoric acid mono-(4-bromo-phenyl) 5.44 [1]
p-Nitrophenyl phosphate 5.20 [4]
Phosphoric acid mono-(4-chloro-phenyl ester) 5.84 [6,7]
Phosphotyrosine 5.55 [8]
Phosphotyrosine 5.80 [9]
Short peptide, Gly-Gly-Tyr(P)-Ala 5.90 [10]
Dodecapeptide 6.10 [11]
Dodecapeptide-phospholipase complex 4.0 [11]
Open in a new tab

Two sets of parameters were determined. First, four phenyl phosphate derivatives were used as reference data. For each molecule of the four, pKa(model) was calculated. Subsequently the four dependencies were averaged. The purpose was to obtain pKa(model), which is independent of small changes in parameterization of the model group. By assumption, the model group in each of both protonation states has the same characteristics in any environment. Second, the pKa values of phosphotyrosine were used for parameterization. There are two published values, 5.80 (Vogel, 1989) and 5.55 (Robitaille et al., 1991), for the experimental pKa values for phosphotyrosine. Parameterizations were performed for both of them, independently.

Application to the tetra- and dodecapeptide and to a complex of the dodecapeptide with phospholipase C-γ1

The methodology described above was applied to predict protonation equilibria for phosphotyrosine in two polypeptide chains, the tetrapeptide (Gly-Gly-pTyr-Ala) and the dodecapeptide (Asp-Asn-Asp-pTyr-Ile-Ile-Pro-Leu-Pro-Asp-Pro-Lys), and for a complex of the latter with the C-terminal SH2 domain of phospholipase C-γ1. The pKa value for phosphotyrosine in the tetrapeptide was determined as 5.90 (Hoffmann et al., 1994). The pKa of 6.1 was determined for phosphotyrosine in the free dodecapeptide, whereas in the complex with the SH2 domain the value of 4.0 was measured (Singer and Forman-Kay, 1997).

RESULTS

ESP charges

All model compounds chosen for parameterization contain the same model group. It is composed of the whole phosphate group and the three carbons from the tyrosine ring, i.e., the CZ, CE1, and CE2 atoms. Table 2 presents the computed, ESP, and B3LYP//6–312+g(d,p) partial charges of the atoms forming the model group in the phenyl phosphate derivatives and related compounds. These charges were common for all the derivatives used for parameterization, and several charges of atoms, like phosphate oxygens, were averaged, assuming the local symmetry. The computed charges, using the 6–312+g(d,p) basis set, are quite large; e.g., at the phosphorus they are +1.50 and +1.85 for the protonated and deprotonated state, respectively. Note that the more negative phosphate group has the more positive phosphorus atom.

TABLE 2.

Atomic charges in the model group

Atom name Mono-anionic form Di-anionic form
H 0.42 –
O3 −0.73 −1.06
P 1.50 1.85
O1 −0.92 −1.06
O2 −0.92 −1.06
OZ −0.50 −0.72
CZ 0.35 0.45
CE1 −0.10 −0.20
CE2 −0.10 −0.20
Open in a new tab

Dependence of pKa(model) on the solute dielectric constant ɛ

Table 3 presents the computed pKa(model) values as functions of the solute dielectric constant, together with the average value over the four phenyl phosphate derivatives used in the parameterization. The differences between the computed dependencies for the phenyl phosphate derivatives can be considered as a measure of errors of our method resulting from the uncertainty of experimental data and approximations of the model. One should note that such approximations are inherent to all molecular modeling methods.

TABLE 3.

The pKa(model) as a function of the solute dielectric constant for the phenyl phosphate derivatives used in this work, and the average value of the pKa(model)

Phenyl phosphate derivatives
Dielectric constant Br Cl H NO2 Average pKa(model)
5 5.41 5.78 5.53 5.68 5.60
6 5.34 5.71 5.50 5.53 5.52
7 5.30 5.67 5.48 5.43 5.47
8 5.26 5.64 5.47 5.35 5.43
9 5.24 5.62 5.46 5.29 5.40
10 5.22 5.60 5.45 5.24 5.38
12 5.19 5.57 5.44 5.17 5.34
14 5.17 5.55 5.43 5.12 5.32
15 5.16 5.54 5.43 5.09 5.31
17 5.14 5.52 5.42 5.04 5.28
20 5.11 5.50 5.41 4.98 5.25
Open in a new tab

Table 4 presents dependence of the computed pKa(model) as a function of the solute dielectric constant, based on two available experimental pKa values for phosphotyrosine, in the ɛ range from 5 to 20. It can be noted that both parameterizations are different from the data obtained for the four derivatives of phenyl phosphate. However, the value of the pKa(model) for the phosphotyrosine data obtained for the measured pKa value of 5.80 and the average dependence derived from the four phenyl phosphate derivatives are close, starting from ɛ = 14.

TABLE 4.

The pKa(model) as a function of the solute dielectric constant for phosphotyrosine. Two available experimental values are taken into account

Dielectric constant Phosphotyrosine pKa(exp) = 5.80* pKa(model) pKa(exp) = 5.55†
4 5.03 4.78
5 5.08 4.83
6 5.13 4.88
7 5.16 4.91
8 5.18 4.93
9 5.19 4.94
10 5.19 4.94
12 5.21 4.96
14 5.22 4.97
17 5.24 4.99
20 5.27 5.02
Open in a new tab

It can also be noted that pKa(model) is the decreasing function of ɛ for the phenyl phosphate derivatives and it is the increasing function for phosphotyrosine. Different dependence of pKa(model) in the phenyl phosphate derivatives and in phosphotyrosine can be explained by interactions of the model group with the charges in its neighborhood, i.e., CD1, CD2, HD1, and HD2. For the phenyl phosphate derivatives these atoms have the net positive charge close to 0. For phosphotyrosine the net charge is ∼−0.1. The negative charge at the nearest neighborhood of the protonation site makes the pKa(model) lower than a positive charge would, and that effect should gradually disappear with the increase of ɛ.

Predicted pKa values for tetra- and dodecapeptide

The tetrapeptide and the uncomplexed dodecapeptide were used to check applicability of our method for prediction of pKa values. Regarding conformational flexibility, those molecules were treated in the same way as described above. For each of them, 2000 structures were sampled from the Langevin Dynamics trajectories with the electrostatic interactions switched off. The pKa(model) value, based on the four phenyl phosphate derivatives or phosphotyrosine, with the corresponding solute dielectric constant, were used to calculate pKa of the phosphate group in these peptides (see Eq. 4).

Calculations for the dodecapeptide complex with phospholipase were carried out for several sets of structures out of 18 deposited in the PDB file (Pascal et al., 1994), beginning from the first six structures up to all 18 structures. This procedure was applied because proper averaging would require knowledge of the probabilities of structures and this information was not available. Nevertheless, starting from the first six structures up to all 18 from the PDB file, the best solute dielectric constant is always in the range of 11–14. All parameterizations of the pKa(model), i.e., two for phosphotyrosine and the third for phenyl phosphate derivatives, give similar accuracy in prediction of the pKa values.

The pKa(model) parameterization derived from the pKa value of 5.55 for phosphotyrosine gives the best agreement with the experimental pKa for the dodecapeptide-phospholipase complex, regardless of the number of structures used in the calculations. However, the same parameterization gives worse agreement with the experiment for tetrapeptide and dodecapeptide in water. The remaining two parameterizations give values of pKa close to each other. These parameterizations give a similar level of accuracy for dodecapeptide complexed with protein as the first parameterization, and moreover, give better agreement with the experimental pKa values of the peptides in aqueous environment.

Tables 5–7 show the best results together with the corresponding solute dielectric constant, along with the results for the most optimal solute dielectric constant, both for each set of parameters. The results of the calculations based on the first eight structures from the PDB file for the peptide-protein complex are presented in Tables, as well as in Fig. 1.

TABLE 5.

The pKa determined experimentally and computed, based on the parameterization for the model compounds

Molecule Experimental pKa Computed pKa for ɛ = 12 Optimal pKa(ɛ)
Tetrapeptide 5.9 5.75 5.90 (ɛ = 7)
Dodecapeptide:
 Uncomplexed 6.1 6.35 6.12 (ɛ = 20)
 Complexed 4.0 3.93 3.93 (ɛ = 12)
Open in a new tab

The results for the optimal ɛ = 12 are presented in column 3. The best results for particular calculations are presented in column 4. The solute dielectric constants used in the calculations are given in the parentheses.

TABLE 7.

The pKa determined experimentally and computed, based on the parameterization for phosphotyrosine with the experimental pKa = 5.80

Molecule Experimental pKa Computed pKa for ɛ = 12 Optimal pKa(ɛ)
Tetrapeptide 5.9 5.61 5.63 (ɛ = 20)
Dodecapeptide:
 uncomplexed 6.1 6.14 6.11 (ɛ = 20)
 complexed 4.0 3.74 4.10 (ɛ = 10)
Open in a new tab

The results for the optimal ɛ = 12 are presented in column 3. The best results for particular calculations are presented in column 4. The solute dielectric constants used in the calculations are given in the parentheses.

FIGURE 1.

FIGURE 1

Open in a new tab

Dependence of the predicted pKa value for phosphotyrosine in the dodecapeptide complexed with phospholipase, on the solute dielectric constant for the three parameterizations described in the text.

Note that the values of the optimal solvent dielectric constant for each of the molecules differ, and spread in range from 7 to 20. The pKa values obtained for the solute dielectric constant from this range differ from that obtained for the solute dielectric constant of 12 not more than 0.25 pH unit. That difference could be considered as an error arising from the applied approximations and it is close to the experimental error. Inclusion of the conformational flexibility does not lower the solute dielectric constant to the value of ∼2, which could be interpreted as arising from the effect of electronic polarization. High value of the solute dielectric constant correlates also with previous results (Gilson and Honig, 1986; Nakamura et al., 1988; Sham et al., 1997; Schutz and Warshel, 2001). One of the present authors (T.G.) also obtained the high solute dielectric constant (12.0) using the CHARMM charges exclusively (Grycuk, 2002). Therefore, it should be noted that arriving at the optimal solute dielectric constant of ∼12 is not a result of using the ESP charges for the titrated phospho residues and the CHARMM charges for other standard amino acids; it is the property of the model. This is quite an important observation because the ESP charges can be easily computed, using ab initio methods, whereas further optimization of the charges (as well as other force field parameters) is not a straightforward procedure.

Fig. 1 presents results for the dodecapeptide complexed with phospholipase for each set of parameters, as functions of the solute dielectric constant.

DISCUSSION

Answering the question whether a phosphate group is single or doubly ionized in a real molecular environment, for example being bound to a protein molecule, is of key importance for studying and understanding the role of phosphorylation processes in activation of biomolecules. In particular, in our previous studies (Błachut-Okrasińska et al., 1999; Antosiewicz et al., 2000) we have shown that the ionization state of phosphate groups may depend, or be coupled to, conformational changes of phosphorylated proteins. Information on ionization states of the phosphate groups is also required when analyzing mechanisms of the phosphorylation processes by kinases and phosphatases at the atomic level. The method proposed in this study allows us to predict pKa values of the secondary ionization of phosphate groups bound to tyrosines in peptides, with accuracy of ∼±0.3 pH units, when the solute dielectric constant of 11–13 is assumed. This promising approach is now being extended to other phosphorylated peptides; in particular, those which contain phosphorylated serine and/or threonine.

It should be noted that although we applied the ESP charges for the phosphorylated molecules, rather than the CHARMM charges, not available for these compounds, it seems to have a little influence on the results of the present work, i.e., on the achieved agreement with the experimental pKa values and the estimated best solute dielectric constant. A very similar solute dielectric constant was obtained based exclusively on molecules fully parameterized with the CHARMM force field (Grycuk, 2002). This suggests that the procedure described here is of quite general applicability.

Summarizing, the main steps of the applied procedure are the following:

  1. Search for experimental pKa values for a model compound (e.g., amino acid), possibly closest to your titratable subunit.

  2. Calculate the ESP charges for all possible protonation states of any new titratable subunit present in your biopolymer. If parameterization for all subunits is available, skip this point.

  3. Define the model group within the titratable subunit which is described by the lowest possible conformational flexibility, and reduced exclusively to those atoms which change their charge during deprotonation.

  4. Perform the Langevin Dynamics simulation for the model compound with the suppressed electrostatic interactions, to generate the representative ensemble of structures (here, 2000 structures).

  5. Perform the Poisson-Boltzmann calculations to determine the electrostatic contributions 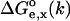Inline graphic for the ensemble of structures in both protonation states and for a selected dielectric constant of the solute molecule. The solvent dielectric constant assumes its experimental value (78 for water).

  6. Apply Eq. 5 to find the pKa(model) for the selected solute dielectric constant.

  7. If you want to optimize the solute dielectric constant (here ∼12), repeat points 5 and 6 for different dielectric constants.

This point completes the parameterization procedure. Now, the computed pKa(model) may be used along with pKa(model) of other groups when performing multiple titration procedure for the biopolymer.

TABLE 6.

The pKa determined experimentally and computed, based on the parameterization for phosphotyrosine with the experimental pKa = 5.55

Molecule Experimental pKa Computed pKa for ɛ = 12 Optimal pKa(ɛ)
Tetrapeptide 5.9 5.36 5.37 (ɛ = 20)
Dodecapeptide:
 uncomplexed 6.1 5.66 5.80 (ɛ = 20)
 complexed 4.0 3.71 4.16 (ɛ = 13)
Open in a new tab

The results for the optimal ɛ = 12 are presented in column 3. The best results for particular calculations are presented in column 4. The solute dielectric constants used in the calculations are given in the parentheses.

Acknowledgments

This work was supported by the Ministry of National Education, Poland (BW 1482/BF) and by the State Committee for Scientific Research, Poland (8T11F01616).

References

  1. Antosiewicz, J., E. Błachut-Okrasińska, T. Grycuk, and B. Lesyng. 2000. A correlation between protonation equilibria in biomolecular systems and their shapes: studies using a Poisson-Boltzmann model. In GAKUTO International Series, Mathematical Science and Applications, vol. 14. N. Kenmochi, editor. Gakkotosho Co., Ltd., Tokyo, Japan. 11–17.
  2. Antosiewicz, J., J. M. Briggs, A. E. Elcock, M. K. Gilson, and J. A. McCammon. 1996. Computing the ionization states of proteins with a detailed charge model. J. Comp. Chem. 17:1633–1644. [Google Scholar]
  3. Antosiewicz, J., J. A. McCammon, and M. K. Gilson. 1994. Prediction of pH-dependent properties of proteins. J. Mol. Biol. 238:415–436. [DOI] [PubMed] [Google Scholar]
  4. Bashford, D., and M. Karplus. 1990. pKa's of ionizable groups in proteins: Atomic detail from a continuum electrostatic model. Biochemistry. 29:10219–10225. [DOI] [PubMed] [Google Scholar]
  5. Beltman, J., W. K. Sonnenburg, and J. A. Beavo. 1993. The role of protein phosphorylation in the regulation of cyclic nucleotide phosphodiesterases. Mol. and Cellular Biochem. 128:239–253. [DOI] [PubMed] [Google Scholar]
  6. Bernstein, F. C., T. F. Koettzle, G. J. B. Williams, E. F. Meyer, M. D. Brice, J. R. Rodgers, O. Kennard, T. Shimanouchi, and M. J. Tasumi. 1977. The protein data bank: a computer-based archival file for molecular structures. J. Mol. Biol. 123:557–594. [DOI] [PubMed] [Google Scholar]
  7. Błachut-Okrasińska, E., B. Lesyng, J. M. Briggs, J. A. McCammon, and J. M. Antosiewicz. 1999. Poisson-Boltzmann model studies of molecular electrostatic properties of the cAMP-dependent protein kinase. Eur. Biophys. J. 28:457–467. [DOI] [PubMed] [Google Scholar]
  8. Bourne, N., and A. Williams. 1984. Effective charge on oxygen in phosphoryl (-PO) group transfer from an oxygen donor. J. Org. Chem. 49:1200–1204. [Google Scholar]
  9. Brunger, A. T., and M. Karplus. 1988. Polar hydrogen positions in proteins: empirical energy placement and neutron diffraction comparison. Proteins: Struct. Func. Gen. 4:148–156. [DOI] [PubMed] [Google Scholar]
  10. Chanley, J. D., and E. Feageson. 1955. The mechanism of the hydrolysis of organic phosphates. III. Aromatic phosphates. J. Am. Chem. Soc. 77:4002–4004. [Google Scholar]
  11. Davis, M. E., J. D. Madura, B. A. Luty, and J. A. McCammon. 1991. Electrostatics and diffusion of molecules in solution: simulations with the University of Houston Brownian dynamics program. Comp. Phys. Commun. 62:187–197. [Google Scholar]
  12. Dekel, N. 1996. Protein phosphorylation/dephosphorylation in the meiotic cell cycle of mammalian oocytes. Rev. Reprod. 1:82–88. [DOI] [PubMed] [Google Scholar]
  13. Feng, M., M. Philippopoulos, A. D. MacKerell, Jr., and C. Lim. 1996. Structural characterization of the phosphotyrosine binding region of a high-affinity domain-phosphopeptide complex by molecular dynamics simulation and chemical shift calculations. J. Am. Chem. Soc. 118:11265–11277. [Google Scholar]
  14. Frisch, M. J., G. W. Trucks, H. B. Schegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. A. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon, C. Gonzalez, and J. A. Pople. 1995. Gaussian 94, Rev. E2. Gaussian, Inc., Pittsburgh, Pennsylvania.
  15. Gilson, M. K., and B. H. Honig. 1986. The dielectric constant of a folded protein. Biopolymers. 25:2097–2119. [DOI] [PubMed] [Google Scholar]
  16. Greengard, P. 1978. Phosphorylated proteins as physiological effectors. Science. 199:146–152. [DOI] [PubMed] [Google Scholar]
  17. Grycuk, T. 2002. Revision of the model system concept for the prediction of pKa's in proteins. J. Phys. Chem. B. 106:1434–1445. [Google Scholar]
  18. Gupta, S. C., N. B. Islam, D. L. Whalen, H. Yagi, and D. M. Jerina. 1987. Bifunctional catalysis in the nucleotide-catalysed hydrolysis of (±)-7 β,8α-dixydroxy-9α,10α-epoxy-7,8,9,10- tetrahydrobenzo[a]pyrene. J. Org. Chem. 52:3812–3815. [Google Scholar]
  19. Hoffmann, R., I. Reichert, W. O. Wachs, M. Zeppezauer, and H. R. Kalbitzer. 1994. 1H and 31P NMR spectroscopy of phosphorylated model peptides. Int. J. Pept. Protein Res. 44:193–198. [DOI] [PubMed] [Google Scholar]
  20. Johnson, L. N., and D. Barford. 1994. Electrostatic effects in the control of glycogen phosphorylase by phosphorylation. Protein Sci. 3:1726–1730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Kalbitzer, H. R., and P. Rösch. 1981. The effect of phosphorylation of the histidyl residue in the tetrapeptide Gly-Gly-His-Ala. Changes of chemical shift and pK values in 1H- and 31P-NMR spectra. Organic Magnet. Reson. 17:88–91. [Google Scholar]
  22. Kimura, E., S. Aoki, T. Koike, and M. Shiro. 1997. A Tris(ZnII-1,4,7,10-tetraazacyclododecane) complex as a new receptor for phosphate dianions in aqueous solution. J. Am. Chem. Soc. 119:3068–3076. [Google Scholar]
  23. King, E. J., and G. E. Delory. 1939. The rates of enzymatic hydrolysis of phosphoric esters. Biochem. J. 33:1185–1188. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Kurosawa, M. 1994. Phosphorylation and dephosphorylation of protein in regulating cellular function. J. Pharmacol. Toxicol. Rev. 31:135–139. [DOI] [PubMed] [Google Scholar]
  25. Maguire, M. H., and G. Shaw. 1953. Synthetic plant hormones. I. Some esters of phosphoric acid. J. Chem. Soc. 1479–1482.
  26. Martinez-Liarte, J. H., A. Iriarte, and M. Martinez-Carrion. 1992. Inorganic phosphate binding and electrostatic effects in the active center of aspartate aminotransferase apoenzyme. Biochemistry. 31:2712–2719. [DOI] [PubMed] [Google Scholar]
  27. Mavri, J., and H. J. Vogel. 1996. Ion pair formation of phosphorylated amino acids and lysine and arginine side chains: a theoretical study. Proteins: Struct. Funct. Genet. 24:495–501. [DOI] [PubMed] [Google Scholar]
  28. Mehler, E. L., and F. Guarnieri. 1999. A self-consistent, microenvironment modulated screened coulomb potential approximation to calculate pH-dependent electrostatic effects in proteins. Biophys. J. 77:3–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Mestas, S. P., and K. J. Lumb. 1999. Electrostatic contribution of phosphorylation to the stability of the CREB-CBP activator-coactivator complex. Nat. Struct. Biol. 6:613–614. [DOI] [PubMed] [Google Scholar]
  30. Nakamura, H., T. Sakamoto, and A. Wada. 1988. A theoretical study of the dielectric constant of protein. Protein Eng. 2:177–183. [DOI] [PubMed] [Google Scholar]
  31. Pascal, S. M., A. U. Singer, G. Gish, T. Yamazaki, S. E. Shoelson, T. Pawson, L. E. Kay, and J. D. Forman-Kay. 1994. Nuclear magnetic resonance structure of an sh2 domain of phospholipase c-gamma 1 complexed with a high affinity binding peptide. Cell. 77:461–472. [DOI] [PubMed] [Google Scholar]
  32. Patarca, R. 1996. Protein phosphorylation and dephosphorylation in physiologic and oncologic processes. Crit. Rev. Oncog. 7:343–432. [DOI] [PubMed] [Google Scholar]
  33. Peacock, C. J., and G. Nickless. 1969. The dissociation constants of some phosphorus(V) acids. Z. Naturforsch. 24a:245–247. [Google Scholar]
  34. Phillips, J. N. 1958. Strength of chloro-substituted phenoxyacetic and related phosphorus-containing acids. J. Chem. Soc. 4271–4276.
  35. Robitaille, P. L., P. A. Robitaille, G. G. Brown, Jr., and G. G. Brown. 1991. An analysis of the pH-dependent chemical-shift behavior of phosphorus-containing metabolites. J. Mag. Res. 92:73–84. [Google Scholar]
  36. Sanchez-Ruiz, J. M., and M. Martinez-Carrion. 1986. Ionization state of the coenzyme 5′-phosphate ester in cytosolic aspartate aminotransferase. A Fourier transform infrared spectroscopic study. Biochemistry. 25:2915–2920. [DOI] [PubMed] [Google Scholar]
  37. Schutz, C. N., and A. Warshel. 2001. What are the dielectric “constants” of proteins and how to validate electrostatic models. Proteins: Struct. Funct. Genet. 44:400–417. [DOI] [PubMed] [Google Scholar]
  38. Sham, Y. Y., Z. T. Chu, and A. Warshel. 1997. Consistent calculations of pK(a)'s of ionizable residues in proteins: Semi-microscopic and microscopic approaches. J. Phys. Chem. 101:4458–4472. [Google Scholar]
  39. Singer, A. U., and J. D. Forman-Kay. 1997. pH titration studies of an SH2 domain-phosphopeptide complex: Unusual histidine and phosphate pKa values. Protein Sci. 6:1910–1919. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Vogel, H. J. 1989. Phosphorus-31 NMR of phosphoproteins. Methods Enzymol. 177:263–282. [DOI] [PubMed] [Google Scholar]
  41. Walaas, S. I., and P. Greengard. 1991. Protein phosphorylation and neuronal function. Pharmacol. Rev. 43:299–349. [PubMed] [Google Scholar]
  42. Weast, R. C. editor. 1966. CRC Handbook of Physics and Chemistry, 47th ed. CRC Press, Cleveland, Ohio.
  43. Westheimer, F. H. 1987. Why nature chose phosphates. Science. 235:1173–1178. [DOI] [PubMed] [Google Scholar]
  44. Widmalm, G., and R. W. Pastor. 1992. Comparison of Langevin and molecular dynamics simulations—equilibrium and dynamics of ethylene glycol in water. J. Chem. Soc. Faraday Trans. 88:1747–1754. [Google Scholar]
  45. Yang, A. S., M. R. Gunner, R. Sampogna, K. Sharp, and B. Honig. 1993. On the calculation of pKas in proteins. Proteins: Struct. Func. Gen. 15:252–265. [DOI] [PubMed] [Google Scholar]
  46. Yang, H. L. S. Z., G. Zhi, A. J. T. Stull, and K. M. Trybus. 1994. Charge replacement near the phosphorylatable serine of the myosin regulatory light chain mimics aspects of phosphorylation. Proc. Natl. Acad. Sci. USA. 91:1490–1494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. You, T. J., and D. Bashford. 1995. Conformation and hydrogen ion titration of proteins: a continuum electrostatic model with conformational flexibility. Biophys. J. 69:1721–1733. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Zhou, H., and M. Vijayakumar. 1997. Modeling of protein conformational fluctuations in pKa predictions. J. Mol. Biol. 267:1002–1011. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES