MC-PHS: A Monte Carlo Implementation of the Primary Hydration Shell for Protein Folding and Design

Abstract

A primary hydration shell (PHS) approach is developed for Monte Carlo simulations of conformationally rich macromolecular systems in an environment that efficiently captures principal solvation effects. It has been previously demonstrated that molecular dynamics using PHS is an efficient method to study peptide structure and dynamics in aqueous solution. Here, we extend the PHS approach to Monte Carlo simulations, whereby a stable shell of water molecules is maintained with a flexible, nonspherical, half-harmonic potential, tuned to maintain a constant restraining energy, with the difference between the restraint and shell energies used to dynamically adjust the shell radius. Examination of the shell and system size dependence of the restraining potential reveals its robustness. Moreover, its suitability for biomolecular simulations is evaluated using small spheres of water, hydration properties of small biological molecules, and configurational sampling of β-hairpin pentapeptide YPGDV. This method, termed MC-PHS, appears to provide efficient representation of dominant solvation effects and should prove useful in the study of protein folding and design.

INTRODUCTION

Structure and stability of proteins result from a delicate balance of the stabilizing interactions of the polypeptide with itself and the destabilizing interactions of the unfolded chain with its solvent environment. As such, solvation plays a cardinal role in protein folding and stability (Dill, 1999). Consequently, proteins exhibit dramatically different properties when observed in gas phase, and short polypeptides generally fail to adopt stable conformations in water. The importance of solvent is further underscored by the failure of continuum models of solvation to recapitulate a wide variety of experimental measures of protein-folding kinetics and thermodynamics. On the other hand, molecular solvation models that treat water explicitly, such as those employed within periodic boundary conditions (PBC), are computationally expensive, limiting sampling of both timescales and phase space.

Thus it is advantageous to consider solvation models that treat water explicitly in the vicinity of the solute, but employ an implicit representation of bulk solvent elsewhere. A number of such formulations has been developed, including a surface constrained all-atom solvent model that emphasizes the treatment of interfacial and bulk electrostatic effects by imposing a number of surface constraints (King and Warshel, 1989). Dynamic surface boundary conditions utilize a restrained dynamic layer of solvent outside the region of interest to reproduce solvent structure and energetics in the vicinity of the solute (Juffer and Berendsen, 1993). The spherical solvent boundary potential replaces bulk water with a continuum representation (Beglov and Roux, 1994), and is attractive because of its analytical treatment of the boundary potential, but falls short of being generally applicable because of its spherical geometry. The shell approximation for protein hydration model uses a number of interfacial approximations and a pressure bath to maintain a molecular solvation layer of appropriate quality around the solute (Lounnas et al., 1999). Finally, the primary hydration shell (PHS) model uses a restraining force beyond the molecular solvation environment of the solute (Beglov and Roux, 1995), and has recently been expanded to include a temperature-dependence term (Rosenhouse-Dantsker and Osman, 2000). In the PHS approach, the continuum representation of solvation has to be obtained from a derivative of the potential of mean force, which is a nontrivial problem but can be applied to general-shape solutes. This is particularly important for polypeptide solutes that may undergo large changes in shape and volume upon folding and conformational sampling. Current implementations of reduced size solvation models are limited to molecular dynamics (MD), and MD simulations are limited in their phase space explorations by time-dependent trajectories. Thus, we sought to develop a primary hydration shell model for Monte Carlo (MC) simulations.

In MC simulations, new molecular configurations of the system are generated by making random structural changes to the internal degrees of freedom and subsequently accepting or rejecting them based on the Metropolis criterion. One of the potential advantages of MC is that the simulation trajectory is a Markov chain of configurations that explores phase space in a time-independent manner, thereby formulating an equilibrium statistical mechanical representation of the system. With sufficient sampling, this can be used to derive a wide variety of thermodynamic parameters. Recent advances with global updates and generalized sampling in MC simulations hold great promise for the ability of this approach to provide insight into the thermodynamics of complex macromolecules (Hansmann and Okamoto, 1999; Tsallis, 1988; Zhou and Berne, 1997). Here, we formulate a primary hydration shell model of arbitrary shape and size for MC simulations, and evaluate its properties using systems of neat water, capped amino acids, and the β-hairpin pentapeptide YPGDV.

THEORY AND METHODS

Molecular systems

Simulations were performed using the all-atom CHARMM27 forcefield and the three-site TIP3P water model (Jorgensen et al., 1983; MacKerell et al., 1998). Systems with periodic boundary conditions were constructed by randomly placing waters into a face-centered cubic cell until appropriate density was reached, using partial specific molecular volume of water of 30 ų. For polypeptide solutes, the number of water molecules was adjusted based on the partial molar volumes of the component amino acids (Perkins 1986). A typical simulation would include on the order of 500 water molecules in a cell with a dodecahedral edge length of ∼20 Å. Systems solvated by the primary hydration shell were constructed by deleting all water molecules outside the PHS radius as measured from the nearest solute heavy atom.

Monte Carlo simulations

MC simulations were performed in the isothermal-isobaric (NPT) ensemble at 298 K and 1 atm, using conventional and a modified force-biased Metropolis procedure as implemented in MMC (Mehrotra et al., 1983; http://inka.mssm.edu/∼mezei/mmc/). Systems were thermalized for 10,000 sweeps, as judged from energy equilibration, and were subsequently evolved for 1,000,000 sweeps, saving every 100th configuration, where one sweep represents one step of all the degrees of freedom, including those of the solute and the solvent. We utilized the shuffled cyclic procedure for solute torsional moves (Mezei, 1981). Bond lengths and angles were kept constant. Both solute and solvent step sizes were optimized to yield acceptance rates of 20–40%. For MC-PHS simulations, the shell radius was updated every third sweep. The nonbonded interaction list for water was truncated at 17 Å on molecule basis, and the solute-solvent energies were treated under the minimum image convention.

Formulation of the primary hydration shell

In principle, a PHS should be able to adopt an arbitrary shape around the solute and capture the principal solvation effects, such as density, solvation energy, and structure of the solvent and the solute. The arbitrary shape of the shell is maintained by imposing a half-harmonic restraining potential at the surface of the molecular hydration layer of N solvent molecules:

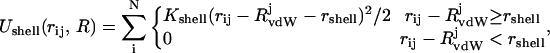(1)

where the energetic penalty is U_shell, experienced by N_out waters that are outside the shell as defined by distance r_shell. K_shell is the restraining force constant; r_ij is the distance between ith solvent and jth solute atoms; and R_vdW^j is the van der Waals radius of the j^th solute atom. In this formulation, water molecules inside the shell do not experience the restraining potential, the shape of which is defined by the force constant. We utilize K_shell of 3.0 kcal/mol/Ų as determined from MD simulations at 300 K (Rosenhouse-Dantsker and Osman, 2000). With appropriate calibration of the reference shell energy, U_ref, and dynamic adjustment of U_shell to approximate U_ref in the course of the simulation, the restraining potential is expected to mimic the steric exclusion provided by the outlying bulk solvent. It is important to note that a primary hydration shell does not necessarily connote a single water layer around the solute. Rather, through the definition of U_shell as a function of r_shell, the boundary becomes arbitrarily adjustable to the specific demands of the system. Thus, the molecular solvation layer is divided into two regions: inner primary hydration layer, which does not experience the restraining potential directly, thereby approximating the primary hydration layer in the presence of bulk solvent, and outer restrained hydration layer, which exists within the restraining potential of Eq. 1 (Fig. 1). In solutions of dynamically fluctuating molecules, such a restraint may be too rigid to allow substantial conformational changes, thereby limiting sampling. To relax this restraint, we allow r_shell to fluctuate. To generate a system that is dynamic and conservative, we define a reference shell energy U_ref and adjust r_shell to minimize the difference between the reference and shell energies. This also enables the molecular solvation layer to adopt arbitrary shapes as they are dictated by the solute. Thus, if the shell energy exceeds U_ref, the shell radius expands, thereby decreasing the number of waters within the restraining potential and their displacement from r_shell, and conversely, shell radius is reduced if the shell energy is below U_ref. The increment Δr, with which the shell radius is updated, is calculated from:

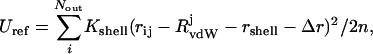(2)

where U_ref is the tuned reference restraining energy (see below), N_out is the number of water molecules within the restraining potential, and n is the number of MC steps. When no waters are present in the outer restrained hydration layer, e.g., U_shell − U_ref = 0, Δr is set to −r_shell/1000, thereby introducing a dynamic fluctuation into the shell radius. When the deviation between U_ref and U_shell is too large to produce real roots in Eq. 2, e.g., U_shell − U_ref ≥ K_shell(r_ij − R_vdW − r_shell)²/2, Δr is set to (〈U_shell〉 − U_ref)/|2U_ref − 2〈U_shell〉|. Such a formulation is analogous to the dynamic adjustments to shell radius of Beglov and Roux, as defined in response to the instantaneous pressure inside the shell in the course of MD simulations (Beglov and Roux, 1995).

FIGURE 1.

Schematic of the restraining potential (dashed) as a function of distance using a sphere of water molecules and its van der Waals surface. The molecular solvation layer is constituted by inner and outer regions. In the inner region (flat), water molecules do not experience the restraining potential directly. In the outer region (parabolic), half-harmonic restraint defined by the force constant, number of waters within the restraining potential, and the square of their displacement from the shell radius, modifies MC moves of the solvent by energetically penalizing presence of water within the outer region.

Because the restraining energy scales with the square of the displacement of water molecules from the shell surface, this creates an instability in its dynamic adjustment, whereby a water molecule that escapes far beyond the shell radius may cause r_shell to increase uncontrollably (data not shown). To prevent this effect, we exclude waters that are outside 3 Å of the shell radius in the calculation of the shell energy, inasmuch as the thickness of the outer region is generally less than 3 Å (data not shown). This ensures that the minimum deviation between U_ref and U_shell is always achieved in the course of the simulation.

Moreover, because the shell energy scales linearly with the number of water molecules within the restraining potential, we introduce normalized shell and specific reference energies, Ū_shell = U_shell/N_out and Ū_ref = U_ref/N_ref, where N_out is the number of waters outside the shell and within the restraining potential, and N_ref is a scaling factor used to produce Ū_ref. In the simulations presented here, we demonstrate that a fixed Ū_ref can effectively replace U_ref, creating a restraint that is also independent of shell size, as it is characterized below.

Analysis

Solute-water and water-water binding energies, radial and orientational distribution functions, and coordination numbers were calculated according to standard methods (Ben-Naim, 1992), referenced to the center of mass of the solute, as implemented in MMC (http://inka.mssm.edu/∼mezei/mmc/). To examine water structure in the vicinity of the solute in MC-PHS and compare it to the behavior of bulk water, we calculated quasi-component distribution functions based on the proximity criterion to assign solvent molecules around a polyfunctional solute (Mehrotra and Beveridge, 1980; Mezei, 1988). Stability of β-hairpin YPGDV relative to the unfolded extended configurations was calculated by summation of the binned distributions of their ψ₃ dihedral angles and hydrogen-bond distances between O(Tyr) and NH(Asp), where K_eq = P_F/P_U, and P_F and P_U are the folded and unfolded state probabilities as defined by their ψ₃ and r_{O(Tyr)-NH(Asp)} values. We estimated the error associated with calculation of these probabilities and the associated folding equilibrium constants by carrying out three independent sets of simulations using different random number seeds for the choices of initial MC moves and their sizes.

RESULTS

In the absence of bulk solvent, unrestrained solvation layers under physiological conditions tend to lose the characteristic water structure and density, leading both to interfacial structuring due to surface tension effects, and evaporation into the surrounding vacuum. The contribution of solvent outside the primary hydration shell can be partitioned into two effects, consisting of explicit interaction and steric exclusion at the interface, and energetic interaction with the bulk, both of which cooperate to maintain appropriate density and structure within the shell. Macroscopically, a component of the energetic interaction with the bulk is expressed in the form of a dielectric screening function. Thus, accurate evaluation of a potential solvation model requires evaluation of both solvation structure and energetics. To examine solvation structure of the shell, we employ the total coordination number k(r), as it is related to the integral of the radial distribution function g(r), and therefore a sensitive measure of solvent organization.

We carried out MC simulations of neat water in spheres 6, 8, and 10 Å in radius, ranging in size from 58 to 356 molecules, using the MC-PHS formalism (Eqs. 1 and 2). To calibrate the restraining parameters, we varied U_ref from 0.001 to 20 kcal/mol, and compared MC-PHS simulations with an equilibrated simulation in periodic boundary conditions. As expected, usage of high U_ref values in the range of 10–20 kcal/mol leads to compression of the PHS and excessive structuring of the internal solvent, as judged from the increased coordination number of water and formation of exaggerated internal solvent structure in PHS relative to PBC (Figs. 2 and 3). On the other hand, inadequate MC-PHS restraint in the form of less than optimal U_ref values, e.g., U_ref < 0.5 kcal/mol, results in decreased coordination numbers relative to PBC, leading to evaporation (Figs. 2 and 3). In the intermediate regime, coordination numbers of MC-PHS water systems mimic that of PBC (Figs. 2 and 3), but do not offer a simple and unambiguous way of obtaining the optimal U_ref. Moreover, the range of U_ref values that yield MC-PHS coordination numbers that are comparable to those of the PBC systems varies with system size, whereby intermediate U_ref values that appear optimal for intermediate size systems lead to solvent compression in smaller systems and solvent evaporation in larger ones. This is evident from Fig. 4, where we show the dependence of 〈r_shell〉 on U_ref for the 6, 8, and 10 Å neat water MC-PHS systems. To minimize the dependence of U_ref on system size, we scale U_shell by the number of water molecules N_out that experience the restraining potential, and replace U_ref and U_shell with specific Ū_ref and the normalized shell energy Ū_shell. In this manner, we evaluate the deviation of MC-PHS behavior from that of bulk water by interpolating 〈r_shell〉 − r_bulk as a function of Ū_ref in Fig. 5, where r_bulk is the shell radius at which the half-harmonic potential restraint of MC-PHS reproduces k(r) of bulk water under periodic boundary conditions. All three systems exhibit a linear dependence of the deviation of PHS radius at which their coordination numbers equal those of PBC systems on Ū_ref, and minimal deviations from PBC behavior with Ū_ref value of 0.15 kcal/mol/molecule (Fig. 5). Indeed, comparison of the radial distribution functions for systems evolved under MC-PHS using Ū_ref of 0.15 kcal/mol/molecule and PBC reveals their near identity (data not shown), consistent with the usage of the coordination number as a calibration parameter for MC-PHS, and in agreement with the usefulness of Ū_ref as a restraining parameter. Thus, as the shell radius is adjusted dynamically after every sweep through the system's internal degrees of freedom, and the specific reference shell energy Ū_ref of 0.15 kcal/mol/molecule is independent of system size within 6–10 Å range, the half-harmonic restraint defined in Eq. 1 formulates a primary hydration shell of arbitrary shape and size.

FIGURE 2.

Total coordination number k as a function of distance r for neat water in periodic boundary conditions (dashed) and 10 Å water drop containing 356 water molecules restrained with MC-PHS (solid) using U_ref of 20 (red), 10 (black), 1 (green), 0.5 (pink), and 0.001 (blue) kcal/mol. Usage of high U_ref values leads to compression of the inner molecular solvation layer, with structuring of water at ∼7 and 9 Å (arrows), whereas inadequate U_ref leads to expansion of the PHS (arrowhead).

FIGURE 3.

Calibration of reference shell energy U_ref based on k(r) for MC-PHS water drops 10 (red squares), 8 (green circles), and 6 (blue diamonds) Å in radius, examining the number of waters inside the shell N_in as a function of mean r_shell. This analysis relates k(r) of PBC simulations (dashed) with N_in(〈r_shell〉) for MC-PHS simulations (solid), which were evolved using U_ref of 0.001–20 kcal/mol. Usage of high U_ref values leads to compression of the drops, as indicated by decrease in the mean shell radius and increase in the coordination numbers, relative to neat water in periodic boundary conditions (dashed), as indicated by upward arrow. On the other hand, inadequate reference shell energies lead to drop expansion, as judged from increases in 〈r_shell〉 and decreases in k(r), as indicated by downward arrow.

FIGURE 4.

Mean shell radii as a function of reference shell energy U_ref for equilibrated MC-PHS water drops 10 (red squares), 8 (green circles), and 6 (blue diamonds) Å in radius. Note that MC-PHS systems are greatly expanded when evolved using low U_ref values, and compressed using high U_ref values, with the intermediate U_ref regime being dependent on system size.

FIGURE 5.

Calibration of size-independent MC-PHS using specific Ū_ref, by interpolating the deviation of r_shell from r_bulk where their k(r) are equal (Fig. 3). Deviation for neat water in periodic boundary conditions (dashed), and MC-PHS water drops 10 (red squares), 8 (green circles), and 6 (blue diamonds) Å in radius. All three systems exhibit minimal deviation from PBC coordination numbers using Ū_ref of 0.15 kcal/mol/molecule.

In addition to interfacial steric exclusion and molecular interactions that maintain appropriate density and structure within the shell, the outlying bulk solvent also provides energetic interaction with the interior, macroscopically recognized as dielectric screening, leading to energetics of solvation characteristic of aqueous solutions. To examine the efficacy of MC-PHS in capturing energetics of solvation, we calculate the distributions of solute-solvent binding energies for PBC and MC-PHS for neat water systems examined above. As can be seen from Fig. 6, both PBC and MC-PHS agree well with established water binding energy values of roughly −20 kcal/mol (Beveridge et al., 1983). The small deviation in the mean binding energy between PBC and MC-PHS may be due to the shortcomings of the particular functional form chosen for MC-PHS and its calibration to completely capture the properties of outlying bulk solvent, but is unlikely, as explained below.

FIGURE 6.

Water binding energy distributions for neat water in periodic boundary conditions (dashed) and MC-PHS 10 Å water drop restrained with Ū_ref of 0.15 kcal/mol/molecule.

Because amino acids exert unique kosmotropic and chaotropic effects on surrounding solvent, we examined the robustness of MC-PHS in reproducing bulk solvation properties as determined from identical respective PBC simulations of four N-acetyl carboxamide amino acids: lysine, glutamate, threonine, and phenylalanine, chosen to represent major physicochemical types of protein components. Capped amino acids were solvated taking into account their partial molar specific volumes, and equilibrated in periodic boundary conditions. Identical simulations were carried out with 6 and 10 Å primary hydration shells. As expected, solute-solvent binding energy distributions for capped amino acids are shifted to substantially lower energies relative to that of neat water (Fig. 7). Both charged and hydrophobic, as well as large and small solutes, are accurately solvated by MC-PHS, reproducing both the mean energy of solvation, as well as its more weakly and strongly bound extremes spanning widely in energy space from −50 to −200 kcal/mol (Fig. 7).

FIGURE 7.

Solute-solvent binding energy distributions for PBC (dashed) and MC-PHS (solid) simulations of capped lysine, glutamate, threonine, and phenylalanine restrained with Ū_ref of 0.15 kcal/mol/molecule in 10 Å MC-PHS. MC-PHS reproduces PBC energetics of solvation of both weakly (Phe and Thr) and strongly (Lys and Glu) interacting solutes.

To examine the fine water structure around various solute functional groups, we calculated various proximity-restricted quasi-component distribution functions (Figs. 8 and 9). MC-PHS accurately reproduces PBC solute-solvent radial distribution function in the vicinity of the amide and carbonyl groups of the peptide backbone, exhibiting both a well-structured first hydration layer and relatively plastic surrounding solvent (Fig. 8). Strikingly, MC-PHS reproduces the orientation properties of water molecules hydrating the NH amide and CO carbonyl groups with opposite orientational dipoles, as evidenced by the opposite orientations of mean water dipole vectors in the first hydration layer (Fig. 8). This orientational effect is restricted to the structured first hydration layer, and is dissipated in the surrounding layers that are unstructured. Similarly, MC-PHS accurately reproduces the water structure around strongly polarizing moieties, such as the lysyl side chain amino group, with a structured and oriented first hydration layer (Fig. 9). On the other hand, water molecules solvating aliphatic surfaces, such as the lysyl side chain C^γ, exhibit little orientation, as expected from their nonpolar nature (Fig. 9). Yet, both first and second hydration shells are ordered, as expected from the hydrophobic nature of the interface (Fig. 9). Moreover, the equivalence of hydration structures between MC-PHS and PBC simulations is apparent from comparisons of solvent-solvent radial distribution functions (Fig. 10).

FIGURE 8.

Solute-solvent radial distribution g(r) and mean water dipole orientational 〈Θ(r)〉 correlation functions for water molecules in proximity to backbone amide carbonyl moieties of N-acetyl carboxamide lysine for PBC (dashed) and MC-PHS (solid) simulations. Note the oppositely oriented water molecules in the first hydration layer of the positively charged amide NH and negatively charged carbonyl CO groups.

FIGURE 9.

Solute-solvent radial distribution g(r) and mean water dipole orientational 〈Θ(r)〉 correlation functions for water molecules in proximity to lysyl side chain terminal amine and lysyl C^γ methylene hydrogens for PBC (dashed) and MC-PHS (solid) simulations. Note the presence of hydrophobic structuring of water molecules solvating the aliphatic C^γ methylene group.

FIGURE 10.

Solvent-solvent radial distribution g(r) correlation functions for water molecules in proximity to lysyl side chain terminal amine and lysyl C^γ methylene hydrogens for PBC (dashed) and MC-PHS (solid) simulations.

To examine the effect of our solvent model on solute behavior, and specifically to examine the ability of MC-PHS to reproduce solute structure and energetics in the context of aqueous solvation, we performed simulations of the pentapeptide YPGDV in a 6 Å MC-PHS layer. This peptide was chosen because it forms a stable reverse β-hairpin in solution, and its structure and thermodynamics are well described using both NMR spectroscopy measurements and MD simulations (Dyson et al., 1988; Karpen et al., 1993). We performed three simulations starting from the folded (β-hairpin), unfolded (extended), and misfolded (α-helical) conformations. It has been observed using nuclear Overhauser effect and ³J_HNHα coupling information from NMR spectroscopy and clustering of MD trajectories that the configurational sampling of YPGDV with respect to the β-hairpin state is nearly completely described by the values of the ψ₃ dihedral angle and O(Tyr)-NH(Asp) intramolecular hydrogen bond in the β-turn (Dyson et al., 1988; Karpen et al., 1993). Thus, we calculated the distributions of ψ₃ and r_{O(Tyr)-NH(Asp)} from simulations of YPGDV starting from the β-hairpin, extended, and α-helical states. As can be seen from Fig. 11, calculation of ψ₃ from all three simulations yields statistically indistinguishable distributions, consistent with the inference that sampling is converged, at least with respect to ensembles that define the stability of the folded state. Solvated by 6 Å MC-PHS, YPGDV interconverts between two populations: the unfolded state characterized by 〈ψ₃〉 of 174°, and the folded state with 〈ψ₃〉 of 282° (Fig. 11), in agreement with its NMR measurements (Dyson et al., 1988). The folded state is additionally defined by the intramolecular hydrogen bond between the backbone carbonyl of Tyr and the amide of Asp, with 〈r_{O(Tyr)-NH(Asp)}〉 of 2.8 Å (Fig. 11 c). Most importantly, MC-PHS accurately reproduces the experimentally observed stability of YPGDV in water (Dyson et al., 1988), using simulations starting from folded, unfolded, and misfolded states, and using either ψ₃ or r_{O(Tyr)-NH(Asp)} as a structural probe (Fig. 11; Table 1). The discrepancy between the stabilities calculated from simulations using unfolded, folded, and misfolded starting structures, and therefore the error associated with possible lack of convergence, is of the order of 0.05 kcal/mol (Table 1), well below the experimental error associated with quantifying populations using NMR spectroscopy (Dyson et al., 1988; Palmer et al., 1991).

a.

Distributions of the value of ψ₃ dihedral angle as calculated from simulations of YPGDV as solvated by 6 Å MC-PHS using starting folded β-hairpin (red dashed), unfolded extended (black solid), and misfolded α-helical (green dotted) conformations. The unfolded state (U) is characterized by 〈ψ₃〉 of 174°, and the folded state (F) with 〈ψ₃〉 of 282°. (b) Distributions of the O(Tyr)-NH(Asp) hydrogen bond distance as calculated from simulations of YPGDV as solvated by 6 Å MC-PHS using starting folded β-hairpin (red dashed), unfolded extended (black solid), and misfolded α-helical (green dotted) states. The folded state (F) is characterized by 〈r_{O(Tyr)-NH(Asp)}〉 of 2.8 Å, whereas the unfolded state (U) exhibits multiple conformations lacking intramolecular hydrogen bonds. (c) Representative structures of the folded state (left) and the unfolded state (right).

TABLE 1.

Configurational sampling of YPGDV in 6 Å MC-PHS

	*		*		†
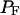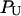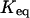Initial state	ψ3	rO(Tyr)-NH(Asp)	ψ3	rO(Tyr)-NH(Asp)	ψ3	rO(Tyr)-NH(Asp)
Folded	0.48 ± 0.03‡	0.52 ± 0.03	0.52 ± 0.02	0.48 ± 0.02	0.92 ± 0.04	1.1 ± 0.03
Unfolded	0.50 ± 0.01	0.51 ± 0.02	0.50 ± 0.02	0.49 ± 0.02	1.0 ± 0.03	1.0 ± 0.03
Misfolded	0.51 ± 0.03	0.49 ± 0.03	0.49 ± 0.03	0.51 ± 0.03	1.1 ± 0.04	0.96 ± 0.04

^*Probabilities of the folded (P_F) and unfolded (P_U) states are calculated from sums of the binned distributions of ψ₃ and r_{O(Tyr)-NH(Asp)}.

^†Folding equilibrium constant is calculated from P_F/P_U.

^‡Values are expressed as ±1σ, as calculated from three independent simulations using different random number seeds for the initial moves.

DISCUSSION

It is somewhat remarkable that a PHS model formulated by a rudimentary half-harmonic restraint is able to accurately reproduce both the energetics and fine structure of solvation of diverse solutes. Although the dielectric permittivity of regions surrounding MC-PHS is close to that of vacuum, and we expected to observe inadequate dielectric screening within the shell, this does not appear to be the case in the current simulations (Fig. 7), perhaps with the exception of those of neat water (Fig. 6), for which MC-PHS yields a slightly higher mean binding energy as compared to PBC simulations (−20.50 vs. −20.78 kcal/mol, respectively). This is likely an insignificant difference, inasmuch as the orientation properties of water, which are extremely sensitive to dielectric effects, are well reproduced by MC-PHS around a variety of polarizing moieties (Figs. 8 and 9). In all, the efficacy of the current implementation of PHS for Monte Carlo simulations stems from two effects: 1), maintenance of accurate water structure and energetics within the PHS by the half-harmonic restraint that mimics steric exclusion by the outlying bulk water; and 2), accurate representation of water structure at the interface by water that is outside of the PHS but within the restraining potential. The latter effect is quite robust as it requires as few as five water molecules on the average in the 6 Å MC-PHS that contains ∼50 water molecules (data not shown), suggesting that as long as proper density of the shell is maintained, fine structure and energetics characteristic of aqueous solvation are self-emergent.

Moreover, MC-PHS accurately reproduces the stability of the β-hairpin pentapeptide YPGDV, regardless of whether the simulation is initiated from the folded, unfolded, or misfolded (α-helical) states (Fig. 11; Table 1). Because the nature of the unfolded state is intimately linked to its solvation by virtue of being solvent-exposed, the ability of MC-PHS to accurately reproduce the experimentally observed native state stability of YPGDV indicates its suitability for theoretical studies of the structure and thermodynamics of flexible polypeptides in the context of explicit aqueous solvation. In this light, equilibrium statistical mechanical studies of the nature of the polypeptide unfolded state and the origin of native state protein stability in the context of explicit aqueous solvation are significant directions of future work. Moreover, usage of the 6 Å MC-PHS seems to overcome the inherent limitations of MC simulations of flexible solutes in condensed phase, where motions of the solute are strongly coupled to those of the solvent.

We have attempted to develop a PHS model for MC simulations that efficiently captures dominant solvation effects in the absence of bulk molecular solvation. Usage of a dynamically adjusted half-harmonic restraining potential allows us to create an arbitrarily shaped molecular solvation layer. Additionally, calibration of this model using a size-normalized Ū_ref parameter of 0.15 kcal/mol/molecule using TIP3P water results in a potential applicable to a PHS of arbitrary size that is amenable to simulations of conformationally rich solutes. Examination of the size-dependence of MC-PHS using droplets of neat water reveals its robustness in accurately reproducing both bulk water structure and energetics. Moreover, MC-PHS accurately reproduces solvation energetics and structure of both highly polar as well as nonpolar amino acid solutes, as revealed by the examination of solvent radial and orientational proximity distribution functions. Most importantly, MC-PHS correctly recapitulates the experimentally observed aqueous stability of β-hairpin pentapeptide YPGDV. Finally, MC-PHS appears to overcome sampling problems associated with MC simulations of flexible solutes in condensed phase by reducing the number of solvent molecules, and thereby more efficiently coupling rearrangements of the solute to those of the solvent. In all, MC-PHS provides a computationally efficient and accurate model of solvation that can be applied to the study of protein folding and design, in which accurate molecular representations of both solute and solvent are of paramount importance.