Hybrid Global Optimization Algorithms for Protein Structure Prediction: Alternating Hybrids

Abstract

Hybrid global optimization methods attempt to combine the beneficial features of two or more algorithms, and can be powerful methods for solving challenging nonconvex optimization problems. In this paper, novel classes of hybrid global optimization methods, termed alternating hybrids, are introduced for application as a tool in treating the peptide and protein structure prediction problems. In particular, these new optimization methods take the form of hybrids between a deterministic global optimization algorithm, the αBB, and a stochastically based method, conformational space annealing (CSA). The αBB method, as a theoretically proven global optimization approach, exhibits consistency, as it guarantees convergence to the global minimum for twice-continuously differentiable constrained nonlinear programming problems, but can benefit from computationally related enhancements. On the other hand, the independent CSA algorithm is highly efficient, though the method lacks theoretical guarantees of convergence. Furthermore, both the αBB method and the CSA method are found to identify ensembles of low-energy conformers, an important feature for determining the true free energy minimum of the system. The proposed hybrid methods combine the desirable features of efficiency and consistency, thus enabling the accurate prediction of the structures of larger peptides. Computational studies for met-enkephalin and melittin, employing sequential and parallel computing frameworks, demonstrate the promise for these proposed hybrid methods.

INTRODUCTION

Proteins are among the most complex molecules found in nature, and among those most vital for cellular processes as they may serve as structural elements, signal receptors, transport channels, and reaction catalysts, among a myriad of other possible functions. Because the function of a particular protein is directly related to the three-dimensional conformation assumed by that protein, the determination of protein structures is an extremely active area of research. The most basic means of resolving a protein structure are through experimental observations, such as x-ray crystallography and certain forms of NMR spectroscopy. However, such methods generally require a great expense of both time and cost, and, moreover, their applicability is limited to a subset of all proteins.

Another way to determine a protein structure is to predict these data through computational means. Such methods rely on the fact that the linear protein information, that is, the amino acid sequence, is readily available, and that there exists a link between the linear sequence information for a given protein and its native three dimensional. This was established experimentally by first isolating and denaturing proteins to produce random, disordered structures, and then restoring physiological conditions thereby prompting the proteins to immediately return to their native conformations (Anfinsen et al., 1961). Such behavior established the thermodynamic hypothesis (Anfinsen, 1973), which holds that the tertiary structure of a protein is uniquely determined by the primary structure.

The task of predicting the three-dimensional structure of a protein given only its primary sequence of amino acids defines the structure prediction in protein-folding problem. A fundamental principle for understanding protein folding relies upon Anfinsen's observation that the native tertiary structure of a protein corresponds to the conformation that minimizes the free energy of the system (Anfinsen et al., 1961). Mathematically, the free energy of a protein can be modeled as functions that mimic the different interaction within the protein system, including nonbonded interactions, hydrogen bonding interactions, hydrophobic interactions, solvent interactions, and entropic effects. These functions depend on the positions of the atoms of that protein, and the native conformation of the protein corresponds to the set of atomic locations providing the minimum possible value of the free energy function.

Because the energy functions are highly nonconvex, the structure prediction in protein folding problem must be treated as a global optimization problem. This is particularly significant for ab initio structure prediction inasmuch as the aid of statistical and database information is not desired. Although it is not yet practical to directly apply global optimization and hope to solve the ab initio structure prediction of medium or large sized proteins using atomistic level models, the development of global optimization techniques remains a key element in the hierarchical and decomposition based approaches used in ab initio structure prediction. Many techniques have been developed and applied to ab initio protein the structure prediction problem with varying degrees of success, and recent reviews can be found elsewhere (Orengo et al., 1999; Lesk et al., 2001). Our recent contributions to ab initio structure prediction (Klepeis et al., 2002b) include an overall multistage approach based on 1), identification of helical segments through partitioning of the protein sequence into overlapping subsequences and performing deterministic global optimization with free energy analysis to determine helical propensities (Klepeis and Floudas, 2002); 2), prediction of β-sheet topology and disulfide bridge networks through the postulation of a β-strand superstructure and using integer linear optimization to maximize the hydrophobic contact energy (Klepeis and Floudas, 2003b); and 3), prediction of the final three-dimensional structure of a protein using a nonconvex constrained formulation and deterministic global optimization techniques (Klepeis and Floudas, 2003a). In all cases, the desired properties of a global optimization approach include consistency and efficiency, such that the location of the minimum energy conformations is guaranteed and is accomplished in a reasonable period of time. Many global optimization algorithms have been developed in an effort to realize these goals. One class of methods relies on probability to perform the optimization, and is termed stochastic global optimization approaches. For example, the conformational space annealing (CSA) algorithm (Lee et al., 1998, 1997, 2000; Lee and Scheraga, 1999; Ripoll et al., 1998;), introduced by Scheraga and co-workers, uses principles taken from genetic algorithms to pass over high-energy conformational states and develop low-energy ones. Other methods can be classified as deterministic because they employ theoretically rigorous procedures to guarantee the location of the global minimum. The αBB algorithm (Adjiman et al., 1998a,b, 2000; Klepeis et al., 1998, 1999, 2002b; Klepeis and Floudas, 1999; Floudas, 2000) is such a method that brackets the global optimum between a nondecreasing series of lower bounds and a nonincreasing series of upper bounds.

The individual strengths and weaknesses of the αBB and CSA algorithms point toward the potential benefits to be gained from a combination of the two algorithms into a single hybrid global optimization approach. As one example, the local minimum conformations obtained during the course of an αBB global optimization run can be used to guide the CSA algorithm by using these minima to generate trial conformations in the CSA. This combination helps to push the selection process toward low energy regions during the course of the branch and bound optimization. It is also possible to use the αBB position of the hybrid to generate seed conformations for the CSA portion so that, in addition to the benefits described above, bank diversity is promoted. Bank diversity increases the chances that structural components necessary for constructing offspring that will represent the global optimum are contained within the bank.

Previous results have verified that the integration of the αBB and CSA algorithms into a single hybrid global optimization approach can be used to enhance performance when compared to the performance of the individual approaches (Klepeis et al., 2002a). In this paper, new classes of hybrid global optimization methods, termed alternating hybrids, are introduced. In this new class of methods, the algorithm alternates between large blocks of αBB iterations and large blocks of CSA iterations. The first test peptide is the five-residue met-enkephalin system, a pentapeptide that has become a frequently used system to benchmark optimization algorithms (Hansmann and Wille, 2002; Lee et al., 1997; Klepeis et al., 1998, 2002b). A more complex system is the membrane bound portion of the protein melittin, a 20-residue polypeptide. A number of alternating hybrids are described and shown to perform better than each independent approach for the met-enkephalin system. Because the alternating hybrids are amenable to parallelization, a parallelized version of the approach is also implemented and shown to locate the potential energy global optimum of melittin in each independent run.

In the sequel, the mathematical formulations needed to represent a protein and to model its free energy, as well the fundamentals of the αBB and CSA global optimization algorithms, are described. Next, the principles behind the hybrid algorithms are presented, and computational results regarding the application of these methods to the met-enkephalin test system are considered. The adaptation of the hybrid algorithms to a parallel computing environment and the application of this parallelized hybrid to a 20-residue system melittin are also discussed.

MATERIALS AND METHODS

Energy modeling

The free energy of a protein depends upon all of the different interactions between the atoms and groups within the protein, and these energies can be expressed as mathematical functions depending on the positions of the atoms in a protein (Floudas et al., 1999). Rigorous application of Anfinsen's hypothesis requires the evaluation of several energetic components, including vacuum potential energy, solvation energy, and entropic contributions (Anfinsen, 1973; Floudas et al., 1999), and although the focus of this work is on the analysis of vacuum potential energy and entropic contributions, the algorithm can be easily extended to include solvation contributions (Klepeis et al., 2002b).

A number of energy formulations has been developed using classical descriptions of molecules, employing basic electrostatics and empirically derived interaction parameters to model interatomic forces. Methods using this general formulation include AMBER (Weiner et al., 1984, 1986), CHARMM (Brooks et al., 1983), ECEPP/3 (Nemethy et al., 1992), ENCAD (Levitt, 1983), GROMOS (van Gunsteren and Berendsen, 1987), and MM3 (Lii and Allinger, 1989a,b). This work employs the ECEPP/3 (Empirical Conformation Energy Program for Peptides) model. Under this model, the lengths of covalent bonds, along with the bond angles, are taken to be constant at their equilibrium value, and the independent degrees of freedom become the torsional angles of the system. The energy formulation used by ECEPP/3 is given by:

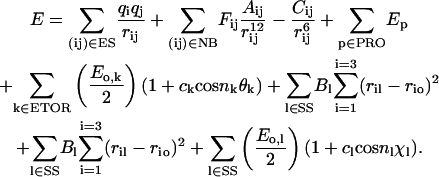(1)

Here, r_ij gives the distance between atoms i and j. q_i gives the effective charge on atom i. F_ij is a distance parameter set equal to 0.5 for 1–4 interactions and to 1.0 for 1–5 and higher interactions. 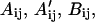and C_ij are empirical parameters giving the strength of nonbonded or hydrogen-bonded interactions for the atom pair ij. E_o,l and E_o,k correspond to rotational barriers for a given dihedral angle. θ_k represents any dihedral angle, and χ_l represents a dihedral angle specifically associated with ring closing in cysteine residues. c_l and c_k take the values ±1, and n_l and n_k give the symmetry class for a particular dihedral angle. A cysteine loop closing energy term and a internal energy for each proline residue are also added (Nemethy et al., 1992).

Accurate calculation of entropic considerations requires the identification of a large collection of low-energy potential energy minima. For proteins, the entropic contribution arises from the ability of the protein to fluctuate among a number of conformationally similar low-energy states (Klepeis and Floudas, 1999). Systems having larger ensembles of low-energy minima that differ only slightly in conformation will therefore have more favorable entropic considerations than systems where a single low-energy conformation is surrounded in the conformational space by unfavorable, high-energy conformations. Methods of determining entropic contributions, and hence conformational free energies, generally involve the development of statistical distribution functions giving the probabilities of the protein occupying each of the available low-energy conformations (Klepeis and Floudas, 1999; Go and Scheraga, 1976; Flory, 1974). The hybrid methods developed in this work will provide an ideal mechanism for generating ensembles of low-energy conformers for free-energy calculations.

Global optimization

The energy functions outlined above are nonconvex functions that generate rugged energy hypersurfaces exhibiting many local minima. To overcome the inherent difficulty of locating the global minimum energy among many local minima, algorithms have been developed for searching the variable space and locating the global optimum without exhaustive enumeration of all local minima. These global optimization algorithms fall into two broad categories—stochastic methods and deterministic methods (Floudas et al., 1999). Stochastic methods are those that involve some element of chance, and thus these methods can not provide theoretical guarantees for finding the global minimum energy solution. On the other hand, deterministic methods are those grounded on mathematical guarantees for consistently finding the global optimum.

The present work introduces new classes of hybrid global optimization methods in an attempt to combine the beneficial features of both the αBB approach, a deterministic branch and bound approach (Adjiman et al., 1998a,b, 2000; Klepeis et al., 1998, 1999, 2002b; Klepeis and Floudas, 1999; Floudas, 2000), and the CSA method, a stochastic method that employs elements of both simulated annealing and genetic algorithms (Lee et al., 1997, 1998, 2000; Lee and Scheraga, 1999; Ripoll et al.). Before describing the algorithmic implementation for the alternating hybrid approaches, the fundamentals of the CSA and αBB algorithms are introduced.

Conformational space annealing

The CSA algorithm, as developed and refined by Scheraga and co-workers (Lee et al., 1997, 1998, 2000; Lee and Scheraga, 1999; Ripoll et al., 1998), belongs to a class of optimization procedures known as simulated annealing algorithms (Kirkpatrick et al., 1983). A simulated annealing algorithm begins with the entire conformation, but as the search progresses, the regions under investigation are gradually narrowed down, with only the most promising (lowest-energy) regions remaining in the active domain. Eventually, the search space is reduced to a small region surrounding the putative global optimum, at which point the algorithm is terminated.

The CSA (Lee et al., 1997) itself represents a hybrid stochastic global optimization approach in that it accomplishes the probing of the search space by combining the elements of a genetic algorithm with the concept of simulated annealing. Genetic algorithms attempt to mimic the biological process of natural selection by introducing variation, involving both individual and sets of variables, into the current population of conformers to produce a new, more fit (lower energy) generation of conformations. Genetic algorithms have had some success in locating the minimum energy conformers for certain protein test problems. A genetic algorithm (LeGrand and Merz, 1993) successfully located the potential energy global minimum (PEGM) for the five-residue oligopeptide, met-enkephalin. However, for larger test problems, such as the 20-residue melittin and 18-residue apamin proteins, the algorithm has had considerably less success (Sun, 1993).

The CSA approach begins with a bank of conformations scattered randomly through dihedral angle space. After generating a set of N_bank random conformations, each conformation is subjected to a local energy minimization using the ECEPP/3 energy force field (Nemethy et al., 1992). This set of conformations is labeled as the first bank, and serves as a repository from which to extract random point mutations for dihedral angle variables. The first bank is also used to define the annealing schedule by first calculating the average distance between the first bank elements in dihedral angle space:

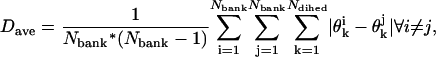(2)

where N_dihed is the number of dihedral angles in the protein to be considered, and 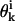is the value of the k^th dihedral angle of the i^th member of the first bank. The initial cutoff radius for the area in dihedral angle space is then defined in terms of this average bank separation:

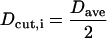(3)

and a schedule is set up to reduce D_cut exponentially so that D_cut is reduced to a value of ∼90° after 5000 minimizations (Lee and Scheraga, 1999).

After establishing this first bank and annealing schedule, the first bank is copied, and the copy is set as the current bank. A seed conformation—that is, an element withdrawn from this bank—takes part in the genetic algorithm portion of the method. Random point mutations are generated by making a copy of the seed conformation and replacing one of its dihedral angle values with the value of the corresponding dihedral angle of a randomly selected first bank element. Such modifications are repeated for any random dihedral angle and for a restricted set composed of the φ, ψ, or χ¹ variables (Lee and Scheraga, 1999). Additional offspring are generated by choosing a contiguous group of dihedral angle variables consisting of ∼⅛ of the total angles in the peptide (Lee et al., 1997), and replacing that group of variables in the seed conformation with those from another, randomly selected conformation in the bank. Note that this procedure uses the bank, not the first bank, because its intent is to simulate crossover between population members, and not random mutation. This procedure is then repeated with even larger sets of dihedral angles called connected groups, each comprising ∼¼ of the total angles in the protein (Lee et al., 1997).

Each trial conformation is subjected to local energy minimization, and the energy of each offspring is then compared with the energy of the highest-energy conformer already in the bank, E^max. If E^trial < E^max, then the offspring is a candidate for entry into the bank, and the dihedral angle values of the offspring are compared with the values for all current bank conformers to identify the closest conformer in dihedral angle space. If this minimum distance between the bank element and the offspring is less than D_cut, then the offspring belongs to the same group as the nearest bank member. Additionally, if the potential energy of the offspring is less than that of the nearest bank member, it replaces this member; if not, the offspring is discarded. If the minimum distance is greater than D_cut, then the offspring represents a new group entirely and it is entered into the bank by deleting the highest energy element in the bank.

This protocol for the generation of offspring is repeated for new seed conformations over a preset number of iterations. Care is taken not to select any bank element as a seed conformation more than once until each element currently in the bank has been used as a seed conformation once (similarly for the second time through the bank). Occasionally, it may be necessary to increase the size of the bank (and the first bank) by adding a number of new, random conformations to them. This may occur, for instance, if the number of iterations reaches a cutoff value without locating the global optimum.

Application of the CSA algorithm to the five-residue met-enkephalin system employed an initial bank of 50 conformers, and involved three unrestricted point mutations, three backbone restricted point mutations, two group crossovers, and two connected group crossovers for each seed conformation (Lee et al., 1997). The PEGM was located in each of 100 independent runs using, on average, 2600 energy minimizations.

The CSA method was also applied to the 20-residue melittin system. Although the bank size was preserved at 50, the number of trial conformations generated per seed conformation was increased to six random and six restricted point mutations, three group crossovers, and five connected group crossovers (Lee et al., 1998). The PEGM was located in only two out of four independent runs. A parallelized version of the CSA (Lee and Scheraga, 1999), in which the generation of trial conformations and bank composition is directed by a central processor, successfully located the global optimum for met-enkephalin in each of 600 independent runs, in an average of ∼35 seconds per run (using 16 processors of an IBM SP2 supercomputer) (Lee and Scheraga, 1999). This algorithm also successfully located the PEGM for melittin in each of 24 independent runs, with an average of 49,000 minimizations (245 iterations) required for each run (Lee and Scheraga, 1999). The average computational requirements for melittin was 4.5 h (using 32 processors of an IBM SP2 supercomputer).

The αBB global optimization approach

The αBB approach is a general deterministic global optimization method (Adjiman et al., 1998a,b, 2000; Klepeis et al., 1998, 1999, 2002b; Klepeis and Floudas, 1999; Floudas, 2000) applicable to a broad range of problems involving twice-continuously differentiable objective and constraint functions, including the problem of structure prediction in protein folding (Klepeis et al., 1998, 1999, 2002b; Klepeis and Floudas, 1999). This algorithm provides a nondecreasing series of lower bounds on the global optimum, and a nonincreasing series of upper bounds on the optimum, with these two series ultimately converging to the global optimum value.

The essence of the algorithm lies in the development of lower bounds on the global minimum through construction of a series of increasingly tight convex underestimators of the ECEPP/3 energy function. The convex underestimators, L for the original energy function E, are generated by the addition of properly scaled quadratic terms (Adjiman et al., 1998a; Klepeis et al., 2002b):

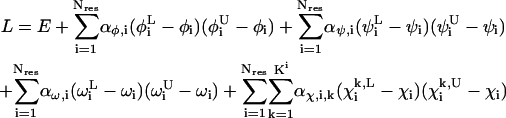(4)

Here, N_res is the number of residues in the peptide chain, and and 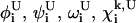give lower and upper bounds on the variables 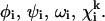The α are nonnegative convexification parameters, which are required to be ≥−½ of the minimum eigenvalue of the Hessian of E over the defined domain (Klepeis et al., 1998; Adjiman et al., 1998a; Floudas, 2000). The exact calculation of the Hessian (and its minimum eigenvalue over a particular domain) can be extremely difficult, and many methods for calculating and providing rigorous estimates of this value have been studied (Adjiman et al., 1998a; Floudas, 2000). For example, one method for the rigorous determination of α parameters for general twice differentiable problems involves interval analysis of Hessian matrices to calculate bounds on the minimum eigenvalue (Adjiman and Floudas, 1996; Adjiman et al., 1998a,b; Floudas, 2000). The valid convex underestimator has the following properties (Maranas and Floudas, 1994; Floudas, 2000):

1. L ≤ E over the entire domain.

2. L = E for all points at which every dihedral angle is at either its lower or upper bound on the domain (corner points).

3. L is convex on the entire domain.

4. The maximal distance between L and E is bounded, and proportional to both α and to the size of the domain in question.

The properties outlined above ensure that, for a subset of a given domain, the convex underestimator L will be tighter than it will be on the original domain, which implies that successive partitioning of the original domain into smaller regions provides tighter convex underestimators and, therefore, a nondecreasing lower bounding sequence. Therefore, the αBB algorithm is implemented (Klepeis et al., 1998, 2002b) through the construction of a branch and bound tree in which the top node corresponds to the entire dihedral angle space. The space is partitioned by branching along a dihedral angle variable with bisection of the bounds for this variable, which produces two subspaces, each having the same variable bounds as the parent node, except for the bounds of the branch variable. A convex underestimator is generated for each subspace, and is subjected to local minimization to generate a lower bound for each subspace. The dihedral angle values corresponding to the local minimum of the convex underestimator are taken as the starting point for a local minimization of the actual ECEPP/3 energy function for each subspace.

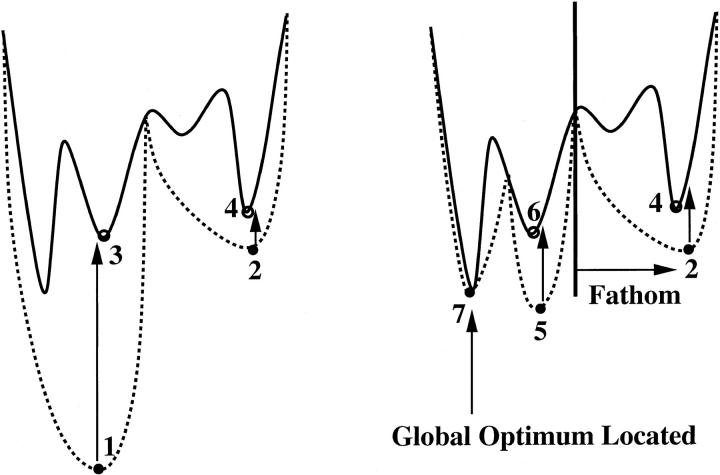
The variable bounds and lower energy bounds corresponding to each of the two subspaces are entered into a list of regions that is ordered according to the energy of the lower bound over each region. The value of the lower bound on the lowest energy region in this list is taken as the initial lower bound, and the local minimization of the original ECEPP/3 function yielding the lowest-energy local minimum is stored as the initial upper bound. An iterative protocol is then applied in which the lowest valued region in the lower bound list is bisected along a branching variable, convex underestimation is applied to both subspaces, and lower and upper bounding minimizations are performed in each subspace. This method for lower bound selection establishes a nondecreasing series of lower bounds on the global optimum. The energies obtained from the two local minimizations of the ECEPP/3 function are compared to the previously stored upper bound; if either is lower, it becomes the new upper bound. In this way, a nonincreasing series of upper bounds is established. Moreover, if the lower bound on a region is higher in energy than the current upper bound on the system, it is not possible for the global minimum to lie in that region, and the region may be eliminated from further consideration (fathomed). After a finite number of iterations, the upper and lower bounds will converge to within a preset tolerance, ɛ, at which point the global optimum has been located, and the algorithm terminates. Fig. 1 provides a one-dimensional illustration of the αBB algorithm (Klepeis and Floudas, 1999).

FIGURE 1.

Illustration of αBB algorithm in one dimension. The domain is first bisected, and the minima of the convex underestimators in the two subdomains are located at 1 and 2. 1 and 2 are each projected upward onto the function and used as starting points for local minimizations of this function, finding the minima at 3 and 4. 3 is the lower of these, so it is taken as the system upper bound. Note that the right-hand side of the domain has a lower bound at 2, which is higher than the system upper bound at 3; this region is therefore fathomed. Further bisection of the left subdomain occurs. At this point, the upper and lower bounds converge at point 7—this point is higher in energy than 5, but lower in energy than 6, meaning that it represents both the upper and lower bound on the system. This indicates that 7 is the global optimum solution.

The αBB algorithm has been successful at locating the global minimum energy solution of met-enkephalin, which was located after ∼1050 iterations and ∼1.3 h of processor time (on an HP-C110 processor). The algorithm has also been used to analyze solvation effects for met-enkephalin, and the global minimum energy was identified after 2.5 h of processor time (Klepeis et al., 1998). A substantive review of the αBB and its applications in protein structure prediction, dynamics of secondary structure formation, and peptide docking can be found elsewhere (Klepeis et al., 2002b).

Hybrid global optimization algorithm

The ultimate goal of developing a hybrid global optimization algorithm is to exploit the beneficial features of two independent algorithms. In other words, the strengths of each algorithm should be enhanced while attempting to minimize any weaknesses associated with these algorithms. In particular, the main strengths of the αBB algorithm are that it provides a theoretical guarantee of convergence to the global minimum, and a range of possible values for the global minimum, as well as a set of lower and upper bounds, are identified. However, the αBB algorithm can be improved on the computational front as it requires solving the additional lower-bounding problems over each domain (Klepeis et al., 1998; Floudas et al., 1999). The CSA algorithm may locate the global optimum relatively quickly (Floudas et al., 1999; Lee et al., 1997), although the approach is not deterministic and the method provides only an upper bound on the global optimum. In fact, unless the global optimum energy is known a priori, the termination criteria could be regarded as heuristic.

One method for capitalizing on the strengths of the αBB algorithm is to use conformations identified as solutions to the upper bounding problem serve as seed conformations or for the generation of offspring in the CSA. This should push the selection process away from high-energy regions inasmuch as the minima found in the solutions to the upper bounding problem are within the region of the problem where it is still feasible that the global optimum could be located. In addition, the lower-bounding functions are constructed by appending the ECEPP/3 energy function, and thus map the low energy regions of the energy function (Klepeis and Floudas, 1999). Because these underestimators are, in turn, used as starting points for local minimizations of the ECEPP/3 function (to solve the upper bounding problem), it follows that the minima so located are more likely to be low in energy than are minima developed by local minimizations of a random point, as is the case for the generic CSA algorithm.

Moreover, the initial bank for the CSA portion can be generated by using local minimum energy conformations identified by the αBB algorithm. This practice capitalizes on the strengths of the αBB approach outlined above, as well as helping to promote bank diversity. In other words, due to the branching along the φ and ψ variables, each minimum originates in a different subdomain of the full variable space, thus covering a broad range of dihedral angle space. Using 50 αBB local minima to constitute the initial CSA bank would therefore represent a way of enforcing initial diversity of this bank, especially with respect to the most critical variables. This diversity, in turn, improves the opportunity to construct offspring that will represent the global minimum energy.

Previous work has shown that a direct integrated and sequential framework for combining the αBB and CSA algorithms into one hybrid global optimization approach can be successful at improving computational performance (Klepeis et al., 2002a). These integrated hybrids are methods in which one iteration of αBB is followed by one or two iterations of CSA, and the local minima generated by αBB are used as seed conformations or for the generation of offspring in the CSA algorithm (Klepeis et al., 2002a). Such hybrid methods provided substantial improvements in computational performance over the stand-alone αBB approach while maintaining the strengths of this deterministic method. However, the parallelized implementation of such an integrated hybrid would result in large communication overhead, thereby leading to the development of alternating hybrid approaches. Along these lines, the current work explores a novel way of combining the αBB and CSA algorithms such that the features of each algorithm work in alternating cycles toward solving the structure prediction in protein folding problem. Upon reviewing the αBB and CSA portions of the hybrids, a detailed description of the alternating hybrid is presented, including issues related to parallelization of the algorithm.

αBB portions of hybrid

The specification of the input parameters to the αBB portions of the hybrid include the definition of dihedral angle variable bounds, as well as the set of variables that are candidates for branching. More specifically, the domains of the φ and ψ backbone dihedral angles are considered for branching, whereas the remaining angles, namely ω, χ, and θ variables, are treated as local variables during the global optimization search. The bounds for each of the φ and ψ variables are initially set to 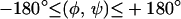whereas the χ variables are set to the values of 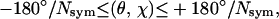where N_sym gives the symmetry class of the dihedral angle.

The algorithm proceeds by branching on the φ and ψ dihedral angles, with the choice of which variable to branch on decided by the variable with the largest current domain. In addition, the α-values used to construct the convex underestimators are not updated but set as initial parameters, inasmuch as the determination of these parameters is computationally expensive.

CSA portions of hybrid

The numbers and types of mutations and crossovers used in the CSA portions of the hybrid algorithms were maintained (Lee et al., 1997) for the five-residue met-enkephalin; that is, each iteration consisted of three random point mutations, three restricted point mutations (φ, ψ, and χ¹ only), two group crossovers (∼⅛ of the total dihedral angles), and two connected group crossovers (∼¼ of the total dihedral angles) (Lee et al., 1997). For the 20-residue melittin system, each iteration consisted of six random point mutations, six restricted point mutations, three group crossovers, and five connected group crossovers (Lee and Scheraga, 1999). The form of the selection and annealing schedule (the schedule by which D_cut is reduced) will be presented in detail in the sequel. The hybrid runs were programmed to halt when the lowest energy element in the CSA bank reached the PEGM (for example, −11.707 kcal/mol for met-enkephalin), or more generally, when the αBB portion of the algorithm indicated convergence.

Alternating hybrids

In the proposed alternating hybrid global optimization approach, the αBB and CSA portions of the algorithm are not integrated (that is, one iteration of αBB is not followed by one iteration of CSA), but rather the two sides of the hybrid take turns dominating the behavior of the algorithm. This so-called alternating hybrid is based on the following procedure. First, the αBB branch-and-bound tree is set up, and the αBB portion of the algorithm is run for N_bank iterations. At each iteration, one of the local minima of the potential energy function generated in solving the upper-bounding problem is stored in a queue. Once N_bank iterations are complete, the queue is emptied into the initial CSA bank. At this point, the αBB algorithm shuts down temporarily, and the CSA portion of the hybrid takes over. One conformation is withdrawn at random from the CSA bank to serve as the seed conformation, and the offspring generated from this conformation are subjected to local minimization and entered into the bank (if applicable). This process is repeated for N_CSA iterations (with restrictions on the choice of a seed to ensure that every element in the bank is chosen once as a seed before any element is chosen a second time).

At this point, if the global optimum has not been located, the CSA portion of the algorithm shuts down temporarily, and control returns to the αBB portion. This proceeds through N_add more iterations to produce N_add more local minima. These minima are then added to the CSA bank, thus increasing its size by N_add. Control then returns to the CSA portion of the algorithm, and the cycle repeats. Care is taken to ensure that all of the new minima added to the CSA bank are used as seed conformations at least once before any of the conformers that were already in the bank are again selected as seed conformations.

Many variants on the alternating hybrid can be implemented by changing certain parameters within the algorithm. The annealing schedule can vary according to a number of different functional relationships. Additionally, the parameters N_bank, N_CSA, and N_add may be varied to change the initial bank size, number of CSA iterations performed between bank updates, and size of the bank updates.

Parallelization

Previous results have indicated that the execution time for the CSA algorithm is roughly proportional to 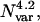where N_var is the number of dihedral angle variables in the problem formulation (Lee et al., 1998). This increase results from two factors—first, a greater number of iterations are required to search the larger variable space, and second, each iteration is more time-consuming because the ECEPP/3 function is more complex, and local minimizations are more computationally expensive (Lee et al., 1998). A viable alternative for treating larger peptides involved adapting the hybrid algorithms to run on multiple processors simultaneously. This type of parallel processing would allow the computational load to be distributed between many processors, thus reducing the wall clock time required for a run to converge.

The structure of the alternating hybrid algorithm is especially amenable to parallelization. Because the αBB and CSA elements of the algorithm are essentially totally separate, two plausible parallelization schemes present themselves. In one scheme, a single “master” processor would direct the operations of the remaining “slave” processors. The master processor would set up the αBB branch-and-bound tree and maintain the list of lower-bounding problems and the CSA bank. However, each node of the αBB branch-and-bound tree would be solved (that is, upper and lower bounds on the function in that region would be generated) by one of the slave processors, having obtained the necessary parameters from the master node. Similarly, the generation of trial conformations and the local energy minimization of such conformations for the CSA portion of the algorithm would also be done by the slave nodes. Each slave processor would alternate between solving αBB problems and generating and minimizing trial conformations for CSA.

This approach has the drawback of leading to sizable amounts of idle time for many of the slave processors. For example, when all of the slaves are in αBB mode, the first slave to finish solving its assigned node will have to idle until all the other slaves are finished—it cannot begin work on the CSA portion of the algorithm, because to set up the CSA bank, it is necessary to have the results from all of the αBB nodes. This will reduce the efficiency of the parallelization and extend the required computation time.

A second alternative involves setting up two “master” nodes—an αBB master and a CSA master node. The slave nodes would then be dedicated to one of these two masters—that is, a given slave node would perform either only αBB iterations, or only CSA iterations. Under this setup, while the CSA nodes are carrying out generation of trail conformations and bank updates, the αBB nodes could be working independently to solve enough lower-bounding problems to prepare for the next required update of the CSA bank. The CSA slaves would be idle at the beginning of the run while they wait for the αBB slaves to generate an initial bank, but it is not likely that this will constitute a significant fraction of the overall run time.

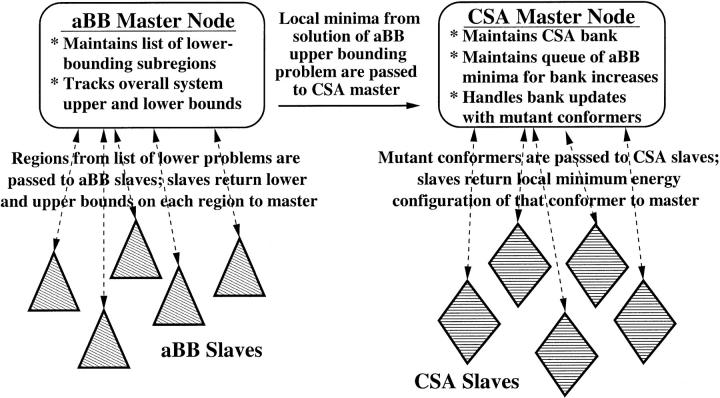
This second alternative was used to implement a parallelized version of the alternating hybrid. A schematic of this implementation is given in Fig. 2. The algorithm begins in the αBB master processor. This processor performs bisections of the dihedral angle space (without solving the lower- or upper-bounding problems on any of the subregions) until enough subregions have been generated to allocate one to each αBB slave. Each slave is assigned a single subregion, and receives as data only the bounds of each dihedral angle variable on this region. The slave solves both the upper and lower bounding problems on this region, and returns both values to the αBB master. The αBB master immediately sends the conformations corresponding to the solutions of the upper bounding problem (that is, local minima of the ECEPP/3 energy function) to the CSA master, which places them in a first in, first out queue. The αBB master then adds the two new subregions to the list of lower bounding problems, takes the first subregion off that list, and assigns that to the slave processor, which just returned its results.

FIGURE 2.

Schematic representation of the methodology used to construct a parallelized version of the alternating hybrid.

The CSA master processor idles until the length of the queue of αBB local minima that it is maintaining equals the required initial bank size. At this time, it empties this queue into the initial bank and begins performing cycles for the generation of offspring. In each cycle, the CSA master selects a seed conformation from the bank and performs point mutations, group crossovers, and connected group crossovers on that seed conformation. Each trial conformation is sent to one of the CSA slave processors, which performs the local energy minimization and returns the results. The CSA master receives these results and updates the bank if necessary. Additionally, the CSA master maintains a list of which slave processors are available to receive work. Only when the number of available slaves equals the number of mutations/crossovers performed per iteration is a new seed conformation selected and new offspring generated. This undoubtedly adds some amount of inefficiency to the implementation by requiring some CSA slaves to idle while they wait for the master to send them their next batch of work. Tests have revealed, however, that the amount of idle time incurred in this way is small compared to the time spent in the actual energy minimizations. Finally, the CSA master constantly communicates with the αBB master, receiving local minima produced by solving the αBB upper-bounding problem and storing these on its queue for use when the CSA bank size needs to be increased.

RESULTS AND DISCUSSION

To provide a basis for comparison between different methods for locating PEGM structures for peptides, two peptides have been adopted as test cases. The performances of different algorithms on the test cases are evaluated and compared.

Met-enkephalin

The first test peptide used in the current work is met-enkephalin. Met-enkephalin (H-Tyr-Gly-Gly-Phe-Met-OH) is a five-residue oligopeptide that occurs naturally in the human brain and in the pituitary gland. The peptide contains 75 atoms that define 24 dihedral angles. As previously noted, it has been estimated that there exist ∼10¹¹ distinct local minima of the potential energy function for this protein (Li and Scheraga, 1988). The putative PEGM for met-enkephalin is −11.707 kcal/mol (Nemethy et al., 1992).

Consistency tests for alternating hybrid

The alternating hybrid algorithm was subjected to extensive testing to determine the consistency with which it was able to locate the PEGM of met-enkephalin. The alternating hybrid algorithm contained three parameters that could be adjusted—the initial CSA bank size, the number of CSA iterations performed between bank updates, and the size of the bank updates. (In practice, the bank update size was always equivalent to the initial bank size.) Eleven different combinations of values for these three variables were chosen, and one alternating hybrid run was performed using each combination, using met-enkephalin as the test system. The annealing schedule for each was set as previously described. However, because the αBB bounds were only updated during the αBB cycles (and not between CSA mutations/crossovers), this resulted in the functional dependence of D_cut on the number of CSA iterations taking the form of a decreasing step function. All runs were allowed to continue until the PEGM was located; the results of these tests are given in Table 1.

TABLE 1.

Results for met-enkephalin runs for alternating hybrids with different operating parameters

Initial bank	CSA iter/cycle	Bank update	Conv	αBB iter	CSA iter
5	15	5	YES	10	26
5	25	5	YES	10	47
10	20	10	YES	30	56
10	30	10	YES	20	51
10	50	10	YES	20	73
20	40	20	YES	300	562
20	60	20	YES	60	144
20	100	20	YES	60	264
50	50	50	YES	50	16
50	100	50	YES	50	16
50	150	50	YES	50	16

Note that one CSA iteration corresponds to one mutate/crossover-and-update cycle (generating 10 trial conformers).

The alternating hybrid successfully located the global minimum for met-enkephalin for all 11 sets of operating parameters chosen. Note that the 20/40/20 (initial bank size/number of CSA iterations per cycle/size of bank update), 20/60/20, and 20/100/20 runs showed significantly poorer performance than any other choice of parameters—each of these three required both more αBB iterations and more CSA iterations to achieve convergence than did any of the other runs. Additionally, the 50/50/50, 50/100/50, and 50/150/50 runs were indistinguishable based upon these tests because convergence was achieved before a bank update occurred under any of these parameter choices.

Based upon these initial results, it was decided to choose five parameter sets for more in-depth consistency testing. Because they performed poorly in the initial tests, the alternating hybrids using 20-member banks were not considered further. Additionally, among the alternating hybrids using 50-member banks, the one using a 3:1 ratio of CSA iterations to αBB iterations was selected for further testing, because, among the hybrids using 5-, 10-, and 20-member CSA banks, the hybrids with a 3:1 ratio of CSA iterations to αBB bank size performed best in each case.

Eleven independent runs were performed on each of the 5/15/5, 5/25/5, 10/20/10, 10/30/10, and 50/150/50 hybrids using met-enkephalin as a test case. To ensure as accurate a comparison between the different hybrids as possible, the same set of 11 random number seeds was used for each hybrids set of 11 runs. For each run, the α-values were set to 7.0, the annealing schedule was set as previously described (taking the form of a step function here), and the runs were allowed to continue until the PEGM was located. A summary of the results from these runs may be found in Table 2.

TABLE 2.

Results of 11 runs on met-enkephalin for each of five sets of operating parameters for the alternating hybrid

Initial bank size	5	5	10	10	50
Number CSA variations per cycle	15	25	20	30	150
Size of bank updates	5	5	10	10	50
% of runs converged	100	100	100	100	100
Average αBB iterations	149	51	120	108	63
Maximum αBB iterations	850	120	760	300	100
Median αBB iterations	80	40	60	80	50
Minimum αBB iterations	10	5	10	20	50
Average CSA iterations	440	242	345	204	85
Maximum CSA iterations	2,542	591	2,253	589	194
Median CSA iterations	161	158	158	140	60
Minimum CSA iterations	17	17	21	25	16

All average iteration values are rounded to the nearest whole number.

The global minimum for met-enkephalin was located in all 11 runs for each of the five sets of parameters under consideration. It can immediately be seen that the 5/15/5 and 10/20/10 hybrids take longer to locate the global minimum than any of the other hybrids. The 5/15/5 alternating hybrid requires the most αBB iterations and the most CSA iterations of any of the five hybrids tested, with the 10/20/10 alternating hybrid requiring the second-most αBB iterations and the second-most CSA iterations. Additionally, for both the 5/15/5 and the 10/20/10 alternating hybrids, the average number of iterations required is more than double the median number required. This indicates that the performances of these hybrids were inconsistent. That is, most of the runs required relatively small numbers of iterations to achieve convergence, but a few outliers required extremely large numbers of iterations. It is not surprising that this inconsistency is found in the algorithms with the combination of smaller bank sizes and smaller numbers of CSA iterations per cycle. Smaller bank sizes reduce the chance of locating the global optimum by limiting the diversity of conformers that may be included within the bank, and lesser numbers of CSA iterations per cycle limit the buildup of low-energy conformers in the bank by constantly diluting the bank with new members.

The picture is somewhat more complicated for the other three alternating hybrids (5/25/5, 10/30/10, and 50/150/50). These three exhibit much lower average numbers of iterations required than the 5/15/5 and 10/20/10 hybrids, and also much tighter distributions of iterations required, as evidenced by the fact that the maximum and minimum numbers of iterations required are much closer together. Significantly, the 50/150/50 hybrid exhibits a very high degree of consistency among the different runs, with all 11 runs requiring either 50 or 100 αBB iterations and between 16 and 194 CSA iterations.

It is not possible to determine which of these three hybrids is the fastest based only upon the data in Table 2. Which hybrid converges more rapidly depends upon the relative times required for one αBB iteration and one CSA iteration; this is explored in the next section.

Computational time comparisons

To accurately assess the relative running times of the various hybrids, it was necessary to do more than merely examine the numbers of iterations required for convergence. Iterations of the αBB portion of the hybrids do not take the same amount of processor time as iterations of the CSA portion of the hybrids. This makes a direct comparison based on iteration numbers impossible for any algorithms that do not execute identical numbers of αBB and CSA iterations.

To provide a standardized measure of the time required for one iteration of αBB and one iteration (10 energy minimizations) of CSA, a time was selected when the external load on the processor was zero (that is, no other users were running jobs). Four tests of the pure αBB algorithm were run for 50 iterations each. The average (wall clock) running time per cycle ranged from a high of 21.04 s to a low of 20.00 s, for an average of 20.37 s. Similarly, four runs of pure CSA were performed, again for 50 iterations each. The wall clock running time in this case ranged from a high of 6.60 s per iteration to a low of 5.80 s per iteration, averaging 6.22 s per iteration. The low variances in both of these sets of runs give a high degree of assurance that the values obtained are, in fact, representative of the actual average running times of one αBB iteration or one CSA iteration.

With these parameters in hand, it is possible to evaluate the standardized average running times of each of the hybrids for which consistency tests on met-enkephalin were performed. These values are given in Table 3, along with values obtained for time trials on runs using either only the αBB portion of the algorithm or runs using only the CSA portion of the algorithm. Because a single αBB iteration takes approximately three times as long as a single CSA iteration, a premium is placed on reducing the number of αBB iterations that must be performed. This explains why the 5/25/5 alternating hybrid has relatively low running times, despite requiring relatively high numbers of CSA iterations. The 50/150/50 alternating hybrid exhibits by far the lowest average running time of any of the hybrid algorithms. This hybrid has the second-lowest αBB iteration requirement, and requires less than one half the number of CSA iterations of the next most efficient algorithm. The 50/150/50 parameter set therefore seems to strike an efficient balance between the relative times that should be devoted to each set of algorithmic features.

TABLE 3.

Average running times (for an HP-C160 processor) on met-enkephalin for hybrid algorithms and for αBB and CSA algorithms alone

Hybrid	Ave αBB iter	Ave time for αBB	Ave CSA iter	Ave time for CSA	Ave total
5/15/5	149	0: 50: 35	440	0: 45: 36	1: 36: 11
5/25/5	51	0: 17: 18	242	0: 25: 05	0: 42: 23
10/20/10	120	0: 40: 44	345	0: 35: 45	1: 16: 29
10/30/10	108	0: 36: 40	204	0: 21: 08	0: 57: 48
50/150/50	63	0: 21: 23	85	0: 08: 48	0: 29: 11
αBB	1069	6: 02: 55	0	0: 00: 00	6: 02: 55
CSA	0	0: 00: 00	299	0: 30: 58	0: 30: 58

All times are based on 11 independent runs, and are given in hours: minutes: seconds.

Naturally, none of the hybrid algorithms would be especially useful if their average running times exceeded those required by a pure αBB algorithm. However, even the slowest hybrid required only 26.5% of the running time of the pure αBB algorithm, with the fastest (50/150/50 alternating hybrid) requiring ∼8.0% of the running time of the αBB. In contrast, it is not strictly necessary for the hybrids to converge faster than the pure CSA algorithm, because they offer advantages, such as a theoretical guarantee of convergence, and the calculation of a rigorous lower bound on the solution, that are not offered by CSA alone. In fact, three of the eight hybrids tested require between 100% and 200% of the running time of the pure CSA algorithm, making these algorithms significantly slower than CSA, but not so much slower as to preclude their use in light of their advantageous theoretical convergence features.

The best hybrid algorithm, the 50/150/50 alternating hybrid, converged (on average) in only 94% of the time required for the CSA algorithm to achieve convergence. An additional set of 10 independent runs performed on the 50/150/50 hybrid and the pure CSA resulted in the 50/150/50 hybrid requiring ∼5% less time to converge than the CSA required. These results strongly suggest that the alternating hybrid scheme has the potential to yield convergence in marginally better time than the CSA alone, although retaining the desirable features of guaranteed convergence and rigorous lower bound calculation.

Met-enkephalin clustering analysis

As previously noted, it is desired that the hybrid algorithms generate a diverse ensemble of low-energy minima for use in free-energy calculations. Several methods for free energy and clustering analysis have been developed, and a number of these have been applied to the enkephalin system (Klepeis and Floudas, 1999; Mitsutake et al., 1998; Meirovitch et al., 1994). As a benchmark of the alternating hybrids' performance in generating such collections of local minima, a free-energy analysis and a clustering analysis were performed on a collection of minima taken from a run of the parallelized 50/150/50 alternating hybrid.

The calculation of free energies for peptide conformers requires that the entropic contribution to the free energy be taken into account. One method for evaluating entropic effects for proteins uses the concept of the harmonic approximation (Go and Scheraga, 1969, 1976; Flory, 1974). Under this approximation, the entropy associated with a particular minimum is given by (Klepeis and Floudas, 1999):

(5)

where Det(H_i) refers to the determinant of the Hessian evaluated at the local minimum, k_B is the Boltzmann constant, and f(T) is a function solely of temperature. The f(T) term is excluded from our calculations when comparing minima at the same temperature to obtain relative free energies.

With this definition in hand, the Gibbs free energy for a particular local minima is given by (Klepeis and Floudas, 1999):

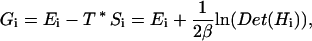(6)

where E_i give the energy at the local minimum in question, and β is equal to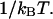

A Boltzmann distribution may now be used to calculate the probability that the protein will occupy a given local minima. The probability that the i^th local minimum will be occupied is given by (Klepeis and Floudas, 1999):

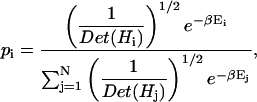(7)

where N represents the total number of minima included in the calculation, and all other terms are as defined previously. A clustering analysis is performed by grouping the local minima based on structural similarity criteria, and calculating the probability that the cluster will be occupied as the additive sum of the probabilities associated with all elements within the cluster.

Free-energy and clustering analyses were performed for a single run of the parallelized 50/150/50 alternating hybrid. The hybrid was allowed to run for 1000 CSA iterations (10,000 energy minimizations), and the energy and dihedral angle values corresponding to the result of each minimization were stored (even if the conformation generated was not ultimately entered into the bank). These minima were sorted to eliminate conformations that appeared multiple times, with the uniqueness criteria being that two unique conformers must differ by at least 50° in at least one dihedral angle variable. The free energy of each minimum was calculated using Eq. 6, for a temperature of 300 K. The minima were then clustered according to their conformations. Specifically, the Zimmerman conformational codes (Zimmerman et al., 1977) for the central three residues were used as a grouping criterion, with all minima having the same values of these codes being placed into the same cluster.

This analysis located 4428 unique conformers (out of 10,000 total conformers) for use in free energy and clustering calculations. The free energy minimum was found to be 14.174 kcal/mol, and both this value and the dihedral angle values for the free energy minimum conformer are in agreement with results reported in the literature (Klepeis and Floudas, 1999). The free energy minimum conformer had a potential energy contribution of −9.899 kcal/mol—∼1.80 kcal/mol higher than the PEGM conformer.

Results of the clustering analysis are presented in Table 4. These results are in agreement with the literature (Klepeis and Floudas, 1999) in identifying the CD^*A cluster as the lowest-energy cluster; however, the literature data indicated that the CD^*A cluster (ranked fourth in the present analysis) was actually the second-lowest energy cluster, and that the AAA cluster (ranked second in the present analysis), was actually the third-lowest energy cluster. It is likely that at least some of this discrepancy originates from the fact that the previous work (Klepeis and Floudas, 1999) used a data set containing 88,000 distinct local minima (as compared with 4428 for the current work). This resulted in a much broader coverage of the dihedral angle space, although at the expense of a greater computational time input. Additionally, the previous work used minima from a pure αBB run (Klepeis and Floudas, 1999). As a result, the minima generated were likely spread more evenly through the dihedral angle space. By contrast, the CSA elements of the hybrid algorithm are designed to lead to clustering of minima in certain low-potential-energy regions, at the expense of exploring the remainder of the dihedral angle space. This has the potential to lead to the underrepresentation of certain clusters in the final analysis. Because the probability of occupation of a particular cluster depends in part upon the number of conformers in that cluster, this bias could help explain the discrepancies in the results above.

TABLE 4.

Results for met-enkephalin clustering analysis at 300 K

Cluster rank	Zimmerman code	Number of conformers	Cluster probability	Cumulative probability
1	CD*A	180	0.2279	0.2279
2	AAA	64	0.1850	0.4229
3	C*DE	100	0.1900	0.6129
4	DC*A	192	0.1340	0.7469

All conformers having the same Zimmerman codes (Zimmerman et al., 1977) for the central three residues were placed in the same cluster. The clusters are ordered by free energy, with cluster 1 having the lowest free energy. Probability refers to the additive sums of the Boltzmann occupation probabilities of all elements in the cluster; cumulative probability refers to the sum of the probabilities of the cluster and all lower-energy clusters.

Melittin

A more complex system is the membrane-bound portion of the protein melittin. This portion of melittin is a 20-residue peptide with the amino acid sequence Gly-Ile-Gly-Ala-Val-Leu-Lys-Val-Leu-Thr-Thr-Gly-Leu-Pro-Ala-Leu-Ile-Ser-Trp-Ile, and contains 113 independent dihedral angles (Lee et al., 1998). The number of local minima present on the energy surface for melittin is not known, although it is believed to be between 10³⁴ and 10⁵⁴ (Ripoll et al., 1998). The putative PEGM for this system is −91.02 kcal/mol (Lee et al., 1998).

Because melittin contains ∼4.7 times as many dihedral angle variables as met-enkephalin, an initial estimate that a CSA algorithm would require 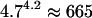times as long to locate the global optimum of melittin as it would to locate the global optimum of met-enkephalin. Although the 50/150/50 alternating hybrid can locate the PEGM for met-enkephalin in 29 min, scaling suggests that the algorithm would require in excess of 13 days to locate the PEGM for melittin. Clearly, if this were true, the hybrid would not be of practical use for locating PEGM structures for peptides of this size.

A few short tests using the melittin system sufficed to demonstrate the timescales that would be involved in applying the 50/150/50 hybrid to melittin using a single processor. The 50 αBB iterations required to establish the initial CSA bank required ∼22 h to complete employing a single processor, or an average of 26 min per iteration. A single CSA iteration (using 10 trial conformations), required ∼8 min to complete in a single processor. A set of 150 such CSA iterations would therefore require ∼20 h to complete in a single processor.

Parallel computing

The parallelized alternating hybrid detailed earlier was employed in investigating the larger protein system, melittin, using an initial CSA bank size of 50, an update size of 50, and (initially) allowed for 500 CSA iterations between bank updates. Initially, the annealing schedule was controlled by the distance between the αBB upper and lower bounds, again resulting in D_cut varying as a decreasing step function of the number of iterations performed. For each seed conformation selected, the algorithm performed six random point mutations, six backbone-restricted point mutations, three group crossovers, and five connected group crossovers.

Prior studies (Ramachandran and Saisekharan, 1968; Vasquez et al., 1983; Zimmerman et al., 1977) have determined that, for amino acids in natural environments, the physically feasible values for the backbone dihedral angles are:

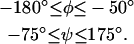(8)

To avoid expending considerable effort in searching infeasible regions of the dihedral angle space, the domain space of all φ and ψ variables was confined to these feasible regions in all tests of the parallel algorithm, although these variable bounds were fully relaxed when solving the upper-bounding problem. (It is worth noting that precisely these restrictions and several additional ones were employed in the CSA implementation (Lee et al., 1997; Lee and Scheraga, 1999).)

With these restrictions on the domains of the φ and ψ variables in place, another run was performed, again using the 50/500/50 parallelized alternating hybrid. This run located a minimum value of −90.416 kcal/mol after 530 CSA iterations (corresponding to ∼10, 600 local minimizations) and after ∼9 h of wall-clock running time (on an array of 68 processors—16 Pentium-III 450 MHz processors, and 52 Pentium-III 600 MHz processors). (The algorithm was allowed to proceed for ∼1000 additional iterations, during which time no lower-energy minima were located.) This value is ∼0.6 kcal/mol higher than the PEGM proposed by Scheraga (Lee et al., 1998; Lee and Scheraga, 1999). However, several minor changes have been made to the ECEPP/3 energy account for this difference, and when the conformation proposed as the PEGM (Lee et al., 1998) is reminimized using the current force field, it produces an energy of −90.416 kcal/mol. The set of dihedral angle values in the proposed PEGM (Lee et al., 1998) is essentially identical to the values found in the present run, as can be seen from the data presented in Table 5. It is therefore taken to be the case that the energy of the PEGM for melittin is −90.416 kcal/mol.

TABLE 5.

Comparison of backbone dihedral angles (φ, ψ) for the two PEGM conformers of melittin

Res	φ	ψ	Res	φ	ψ	Res	φ	ψ	Res	φ	ψ
1	69	−96	11	−74	−43	1	69	−97	11	−75	−41
2	−82	−28	12	−76	−30	2	−82	−28	12	−76	−30
3	−66	−27	13	−148	78	3	−66	−27	13	−147	75
4	−69	−27	14	−69	86	4	−69	−27	14	−69	81
5	−83	−45	15	−154	173	5	−83	−45	15	−150	172
6	−83	72	16	−57	−31	6	−83	72	16	−58	−30
7	−64	−40	17	−56	−45	7	−64	−40	17	−56	−44
8	−66	−41	18	−82	−32	8	−66	−41	18	−82	−32
9	−70	−36	19	−68	−33	9	−70	−36	19	−69	−33
10	−76	−28	20	−79	−46	10	−77	−27	20	−79	−46

The values on the left represent the structure identified in this work. When reminimization is performed with the starting point given by the second solution (Lee et al., 1998), the PEGM reported here is generated.

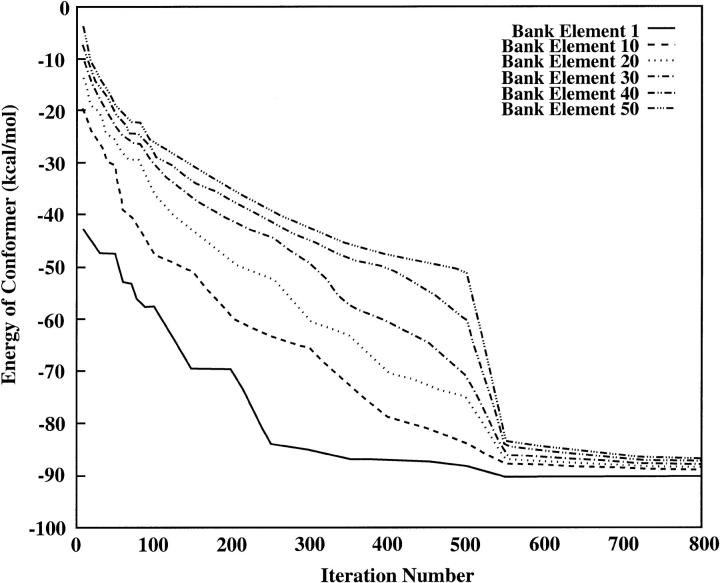
The progress of the CSA algorithm during the course of this run was monitored by tracking the energies of the conformations occupying certain positions in the bank (e.g., the lowest-energy element, 10th-lowest-energy element, and so forth). Fig. 3 provides this data in graphical form.

FIGURE 3.

Plot of energies for elements occupying selected positions within CSA bank as a function of iteration. This test run used a 50/500/50 alternating hybrid to search for the PEGM of melittin; the annealing schedule took the form of a step function. Note that the PEGM was located at iteration 530.

The most conspicuous feature of this graph is the precipitous decline in the energies of the elements at all positions in the bank immediately after iteration 500. This is a direct result of the fact that D_cut is directly proportional to the separation between the αBB upper and lower bounds, and that it is updated only when the bank is updated (that is, at multiples of 500 iterations). Just before the bank update, at iteration 499, D_cut was approximately equal to 1650°, whereas immediately after the bank update, at iteration 501, the value of D_cut had fallen to 385°. The consequence of this is that, before the bank update, the large value of D_cut resulted in the low-energy regions of the dihedral angle space being represented by only a few conformers in the bank, allowing for the presence of many high-energy conformations. As soon as D_cut was reduced, however, many more representatives of the low-energy regions of the dihedral angle space were allowed into the bank simultaneously, resulting in a sudden clustering of the bank elements in these regions, and a concomitant drop in the energies of representative bank elements.

Although this implementation successfully located the PEGM, there are issues to address. Because each seed conformation is used to generate 20 trial conformers, when the value of D_cut is suddenly reduced, it is possible that the bank could quickly become dominated by offspring of only a few (in theory, as few as five or six) trial conformations. This would potentially reduce the diversity of the bank, thus limiting the effectiveness of future crossovers. If bank conformations lying close to the global optimum (but not necessarily having extremely low energies) are eliminated in this sudden bank clustering, it is possible that it will become difficult to locate the global optimum.

To explore alternatives that might avoid this drawback, a linear annealing schedule was introduced that was dependent on the CSA iteration number. The inherent drawback with such a procedure is that it requires fixing the schedule a priori, which in turn assumes at least some knowledge of the system under study. To compensate for this loss of generality, it was decided to allow the number of CSA iterations between bank updates to be determined, not by a fixed number of iterations, but by a fixed number of rounds. That is, bank updates were set to occur not after 500 iterations, but after five rounds—after each element in the bank had been used as a seed conformation five times. Because rounds of iterations take significantly longer when improvements are being made frequently (because the improved offspring themselves enter the bank and must be used before the round ends), this formulation delays updating the CSA bank until the elements in the bank are no longer improving at a rapid pace. Under this formulation, D_cut was defined by

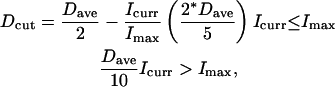where D_ave represents the initial average distance between bank elements, I_curr is the current number of iterations since the last bank update, and I_max is the maximum number of steps in the annealing schedule.

Two independent runs were conducted using the annealing schedule described above, and setting I_max equal to 1000. For both runs, the PEGM at −90.416 kcal/mol was located—after 930 CSA iterations (18,600 local minimizations) and ∼17 h wall-clock running time in the first run, and after 1070 CSA iterations (20,140 local minimizations) and 20 h wall-clock running time in the second (on an array of 68 processors—16 Pentium-III 450 MHz processors, and 52 Pentium-III 600 MHz processors).

A graph tracking the energies of selected elements within the CSA bank for a successful run is given in Fig. 4. One obvious difference between these results and those shown in Fig. 3 is the absence of a sharp discontinuity in the energies of the bank elements. Although this is to be expected for the run depicted (because no bank size increases occurred during the run), other runs using the same annealing and update schedules did not exhibit a sharp discontinuity even at points where a bank update occurred. Rather, the bank size change was marked by a more subtle change in the slopes of each of the energy curves.

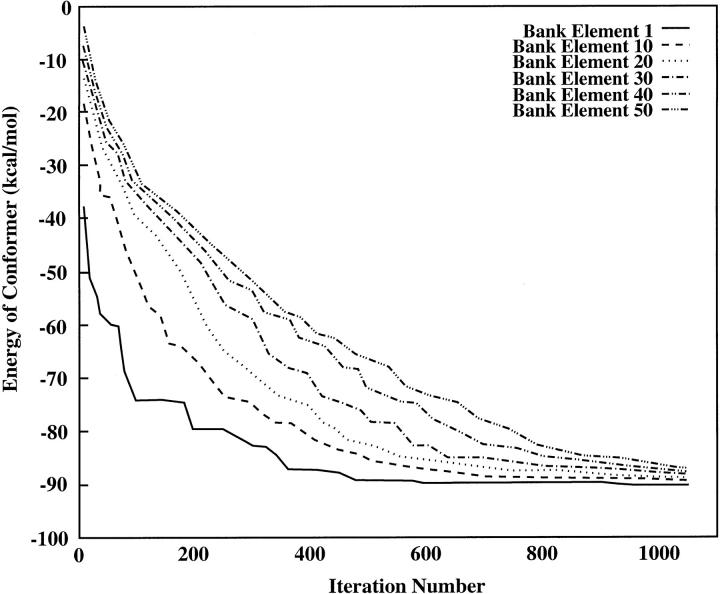
FIGURE 4.

Plot of energies for elements occupying selected positions within CSA bank as a function of iteration. This test run used an alternating hybrid with a linear annealing schedule (I_max = 1,000) and a five-round wait between bank updates. Note that the PEGM was located at iteration 930. No bank size increases occurred during this run.

Interestingly, although the lower-energy contour plots exhibit sharp exponential decreases, the exponential decreases grow progressively shallower as energy increases, and in fact the plot for the 50th bank element is practically linear over a substantial portion of its range (from 100 to 800 iterations.) This reflects the fact that it takes only one or two extremely favorable mutations/crossovers to lower the energy of the first or tenth element in the bank by a substantial amount, and hence these energy plots fall off rapidly. However, the energy of the 50th element is usually lowered when a new group enters the bank and the old highest-energy conformer is replaced with the second-highest-energy conformer. Because the energy difference between the 50th and 49th elements is likely to be rather small (and because this difference remains relatively constant through most of the run, until the elements start becoming strongly clustered at iteration 800), it is logical to expect that the energy of the 50th bank element will decrease more slowly and in a more linear fashion than the energy of the first bank element.

Melittin clustering analysis

Free-energy and clustering analyses were performed on data from an application of the parallelized alternating hybrid to melittin. Free energy and clustering analyses followed the procedure previously described, except that clustering was performed using the Zimmerman codes (Zimmerman et al., 1977) for the 18 interior residues as the clustering criterion. The alternating hybrid was set to use a 1000-step linear annealing schedule and to increase the CSA bank size after every five rounds of iterations. The energies and dihedral angle values of each bank element were recorded after every 10 CSA iterations (an attempt to record the energies and dihedral angle values of each trial conformer was impractical owing to the excessive running time this amount of data would have required for the clustering analysis). The alternating hybrid located the PEGM conformation after 1070 iterations and was immediately terminated.

A total of 807 unique conformers were identified (out of ∼2140 total conformers analyzed); these were subjected to both free-energy and clustering analyses. The free-energy analysis (at 300 K) revealed a free-energy minimum of 49.915 kcal/mol; this structure had a Zimmerman code (for the inner 18 residues) of AAAAAAAAAAADCEAAAAA and a potential energy contribution of −87.400 kcal/mol (almost exactly 3.00 kcal/mol higher than the PEGM).

The results of the clustering analysis are given in Table 6. It can be seen that ∼250 of the 807 unique conformers fall into two clusters having a combined occupation probability in excess of 99.6%. These two clusters are α-helical in nature, differing only in the conformation at the sixth residue (leucine). The high occupation probability for these two clusters strongly suggests that the conformation of melittin is largely α-helical in nature, with bends at residue 6 and residues 13–15. This result is consistent with the qualitative depictions of the native structures (Lee et al., 1998). Note that the free energy global minimum falls into the lowest-energy cluster. The PEGM has a Zimmerman code of AAAACAAAAAADCEAAAAA and falls into the second-lowest-energy cluster. The conformations of the PEGM and the lowest free energy representative of the lowest-energy cluster are shown in Fig. 5.

TABLE 6.

Results for melittin clustering analysis at 300 K

Zimmerman code	No. of confs	Cluster prob	Cumul prob
AAAAAAAAAAADCEAAAAA	103	0.8931	0.8931
AAAACAAAAAADCEAAAAA	142	0.1031	0.9962

All conformers having the same Zimmerman codes (Zimmerman et al., 1977) for the central 18 residues (residues 2–19) were placed in the same cluster. The clusters are ordered by free energy, with cluster 1 having the lowest free energy. Probability refers to the additive sums of the Boltzmann occupation probabilities of all elements in the cluster; cumulative probability refers to the sum of the probabilities of the cluster and all lower-energy clusters.

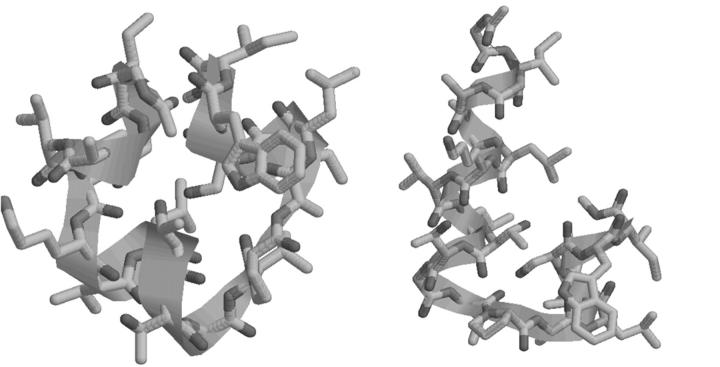
FIGURE 5.

Plot of PEGM (left) and lowest free-energy representative of lowest free-energy cluster (right) for melittin.

CONCLUSIONS

In this work, the goal was to create an efficient, consistent procedure that combines desirable elements from the αBB and CSA algorithms while eliminating or minimizing the drawbacks associated with these methods. The incorporation of features from the αBB algorithms provided a theoretical guarantee of convergence to the global optimum within a finite number of iterations, whereas features adapted from the CSA algorithm provided rapid identification of the global solution and helped to generate large ensembles of low-energy minima for use in free-energy calculations.

The novel class of hybrid global optimization approaches, termed as alternating hybrids, cycle between large blocks of αBB iterations and large blocks of CSA iterations. Analysis of these runs indicated that alternating hybrids with larger initial bank sizes and higher ratios of CSA iterations per cycle to bank size tended to exhibit a greater consistency of performance, with the numbers of iterations required for convergence on the various runs falling within a narrow range, and with no runs requiring an exceptionally large number of iterations relative to the mean.

The results also revealed that the hybrids exhibited significant improvements in running time over a pure αBB algorithm. Moreover, a comparison of the hybrid running times with the running time for a pure CSA algorithm revealed that best results were obtained for the 50/150/50 alternating hybrid, which located the met-enkephalin PEGM in an average of 29.18 min, as opposed to 30.97 min for the pure CSA algorithm. A second set of 11 independent runs confirmed that the 50/150/50 alternating hybrid converged, on average, in 94% of the time required for the CSA algorithm alone to converge.

A version of the alternating hybrid was adapted to make use of a distributed, parallel computing environment. Tests of the parallelized version of the alternating hybrid on melittin resulted in the location of the global optimum in each of two independent runs, requiring less than 20 wall clock h on a set of 68 processors running Linux.

The alternating hybrid algorithm was also shown to provide ensembles of low-energy minima, a necessity in the rigorous calculations of entropic contributions for protein systems. A free-energy and clustering analysis was performed for both test systems and the results are in agreement for studies presented in the literature (Klepeis and Floudas, 1999; Lee et al., 1998).

In conclusion, the alternating hybrid algorithm developed in this work shows potential as a valuable new global optimization algorithm that can serve as one tool for treating the protein structure prediction problem. Although it is not practical to directly apply any one global optimization algorithm and simply solve the ab initio structure prediction in protein folding problem, the αBB-CSA hybrid is able to combine the most desirable features of two individual algorithms. With some overhead, the αBB directs the more rapid CSA such that either convergence or, at the very least, rigorous upper and lower bounds on the global minimum can be obtained. Using these deterministically based bounds, rigorous termination criteria can be imposed, and the need for multiple stochastic-based runs can be avoided. The use of the αBB-based hybrid approach in an hierarchical or decomposition scheme for ab initio protein structure prediction has the added benefit of being able to rigorously treat systems with nonconvex twice-continuously differentiable constraints.